- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логическое следствие и метод резолюций презентация
Содержание
- 1. Логическое следствие и метод резолюций
- 2. Проблема дедукции
- 3. Теоремы проблемы дедукции
- 4. Следствия для заданного множества формул Для заданного
- 5. Резольвента дизъюнктов логики высказываний
- 6. Примеры резольвент
- 7. Метод резолюций в логике высказываний
- 8. Метод резолюций
- 9. Метод насыщения уровня
- 10. Пример метода насыщения уровня
- 11. Недостаток метода насыщения уровня
- 12. Стратегия вычеркивания
- 13. Пример стратегии вычёркивания
- 14. Недостатки стратегии вычёркивания Ясно, что необходимые вычисления
- 15. Лок-резолюция Идея лок-резолюции состоит в использовании индексов
- 16. Лок-резолюция, пример 1
- 17. Лок-резолюция, пример 2
- 18. Теорема о полноте лок-резолюции
- 19. Хорновские дизъюнкты
- 20. Метод резолюций для хорновских дизъюнктов
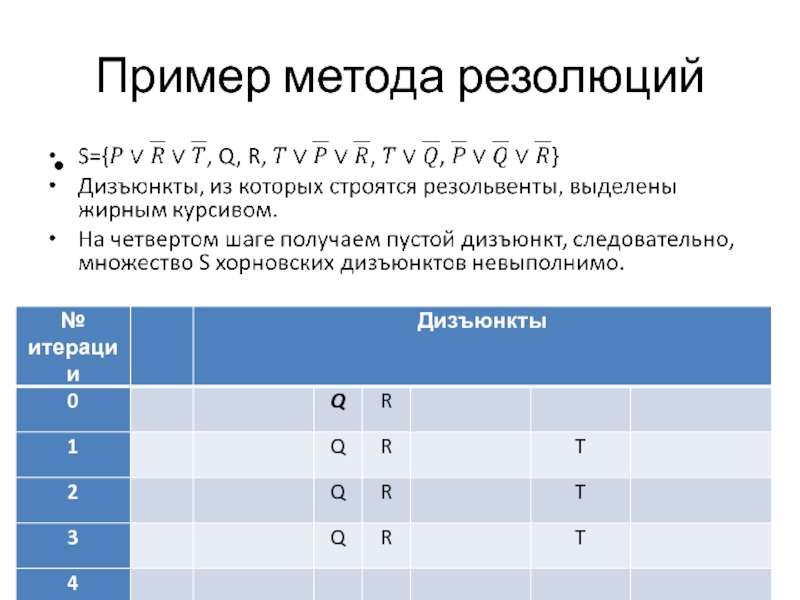
- 21. Пример метода резолюций
- 22. Преобразование формул логики предикатов слайд 1
- 23. Преобразование формул логики предикатов слайд 2
- 24. Исключение кванторов существования
- 25. Сколемовские функции
- 26. Стандартная форма функции
- 27. Многозначность стандартной формы
- 28. Теорема о противоречии
- 29. Унификация Процесс унификации является основным в формальных
- 30. Частные случаи литерала и подстановки
- 31. Применение подстановки к литералу
- 32. Унификатор
- 33. Алгоритм унификации
- 34. Теорема Робинсона Теорема Робинсона. Описанный выше алгоритм
- 35. Пример унификации 1 слайд 1
- 36. Пример унификации 1 слайд 2
- 37. Пример унификации 2
- 38. Метод резолюций в логике предикатов слайд 1
- 39. Метод резолюций в логике предикатов слайд 2
- 40. Пример метода резолюций
- 41. Резольвента дизъюнктов
- 42. Проблема дедукции логики предикатов
Слайд 4Следствия для заданного множества формул
Для заданного множества формул А1, А2,…,Аm, m≥1,
строим их конъюнкцию: С=А1&А2&…&Аm. Для С находим с.к.н.ф.: С= D1&D2&…&Dk, здесь Di, 1≤i≤k, элементарные суммы (дизъюнкты). Теперь по показанной выше теореме получаем, что каждый дизъюнкт Di, 1≤ i≤ k, а также их конъюнкции являются следствиями из А1, А2,…,Аm, m≥1, т. е. имеем: А1, А2,…,Аm╞ Di для любого i, 1≤ i≤ k;
А1, А2,…,Аm╞ Ds1& Ds2&...& Dsr, для любого r, 1≤ r≤ k и любых s1, s2,…,sr, 1≤ s1, s2,…,sr ≤ k.
А1, А2,…,Аm╞ Ds1& Ds2&...& Dsr, для любого r, 1≤ r≤ k и любых s1, s2,…,sr, 1≤ s1, s2,…,sr ≤ k.
Слайд 14Недостатки стратегии вычёркивания
Ясно, что необходимые вычисления не уменьшаются, а увеличиваются. Чтобы
использовать стратегию вычеркивания, необходимо уметь определять, является ли полученный дизъюнкт тавтологией или является ли один из дизъюнктов поддизъюнктом другого.
Метод резолюций позволяет автоматизировать доказательство теорем. Показано, что неограниченное применение резолюции может порождать много лишних и ненужных дизъюнктов наряду с полезными. Хотя можно использовать стратегию вычеркивания, чтобы выбросить некоторые из этих ненужных и бесполезных дизъюнктов после того, как они порождены, на их порождение уже потеряны ресурсы. Далее, если порождены бесполезные дизъюнкты, то нужны ресурсы для того, чтобы определить, что эти дизъюнкты действительно лишние и ненужные. Поэтому для получения эффективных процедур доказательства теорем необходимо не допускать порождения большого числа бесполезных дизъюнктов. Имеются различные подходы к уменьшению вычислений, среди них: метод семантической резолюции; лок-резолюция; линейная резолюция и др. методы.
Метод резолюций позволяет автоматизировать доказательство теорем. Показано, что неограниченное применение резолюции может порождать много лишних и ненужных дизъюнктов наряду с полезными. Хотя можно использовать стратегию вычеркивания, чтобы выбросить некоторые из этих ненужных и бесполезных дизъюнктов после того, как они порождены, на их порождение уже потеряны ресурсы. Далее, если порождены бесполезные дизъюнкты, то нужны ресурсы для того, чтобы определить, что эти дизъюнкты действительно лишние и ненужные. Поэтому для получения эффективных процедур доказательства теорем необходимо не допускать порождения большого числа бесполезных дизъюнктов. Имеются различные подходы к уменьшению вычислений, среди них: метод семантической резолюции; лок-резолюция; линейная резолюция и др. методы.
Слайд 15Лок-резолюция
Идея лок-резолюции состоит в использовании индексов для упорядочения литер в дизъюнктах
из данного множества S дизъюнктов. Иными словами она включает введение индексов для каждого вхождения литеры в S некоторым целым числом; разные вхождения одной и той же литеры могут быть индексированы по-разному. После этого отрезать (удалять) разрешается только литеры с наименьшим индексом в каждом из дизъюнктов. Литеры в резольвентах наследуют свои индексы из посылок. Если литера в резольвенте может унаследовать более одного индекса, то ей ставится в соответствие наименьший индекс.
Слайд 29Унификация
Процесс унификации является основным в формальных преобразованиях, выполняемых при нахождении резольвент
(для метода резолюций).
Пусть задано множество дизъюнктов. Каждый дизъюнкт составлен из литералов.
Пример. Пусть имеем следующее множество дизъюнктов:
Термы литерала могут быть переменными, постоянными или выражениями, состоящим из функциональных букв и термов. Например, для литерала P(x, f(y), b) имеем, что х – переменная, f(y) – сложный терм, b - постоянная.
Пусть задано множество дизъюнктов. Каждый дизъюнкт составлен из литералов.
Пример. Пусть имеем следующее множество дизъюнктов:
Термы литерала могут быть переменными, постоянными или выражениями, состоящим из функциональных букв и термов. Например, для литерала P(x, f(y), b) имеем, что х – переменная, f(y) – сложный терм, b - постоянная.
Слайд 34Теорема Робинсона
Теорема Робинсона. Описанный выше алгоритм находит наиболее общий унификатор для
множества унифицируемых литералов и сообщает о неудаче, если литералы неунифицируемы.