функции p(x) и g(x) – постоянные величины.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейные ДУ второго порядка с постоянными коэффициентами презентация
Содержание
- 1. Линейные ДУ второго порядка с постоянными коэффициентами
- 2. Уравнение вида называется линейным ДУ с постоянными коэффициентами 9
- 3. Где у – искомая функция, p, g
- 4. Рассмотрим сначала однородное уравнение: Будем искать
- 5. Это уравнение называется характеристическим уравнением для уравнения (10).
- 6. Вид решения линейного однородного ДУ (10) существенно
- 7. ТЕОРЕМА. Если корни характеристического уравнения вещественные
- 8. Если корни характеристического уравнения вещественные и
- 9. Если характеристическое уравнение не имеет вещественных
- 10. ПРИМЕРЫ. Решить дифференциальное уравнение: 1
- 11. Решение: Корни вещественные и разные, поэтому общее решение будет иметь вид:
- 12. Решить дифференциальное уравнение: 2
- 13. Решение: Корни вещественные и одинаковые, поэтому общее решение будет иметь вид:
- 14. Решить дифференциальное уравнение: 3
- 15. Решение: Корни комплексные, поэтому общее решение будет иметь вид:
- 16. Теперь рассмотрим решение неоднородного ЛДУ с постоянными
- 17. ПРИМЕР. Решить дифференциальное уравнение:
- 18. Решение: Сначала находим общее решение однородного уравнения:
- 19. Корни вещественные и разные, поэтому общее решение
- 20. Пусть Тогда Подставляем в уравнение:
- 21. Получаем:
- 22. Вычитаем из второго уравнения первое: Теперь подставляем в первое уравнение:
- 23. Интегрируем эти выражения: Частное решение неоднородного уравнения имеет вид: Общее решение будет:
- 24. Частное решение неоднородного уравнения можно найти, используя следующую схему:
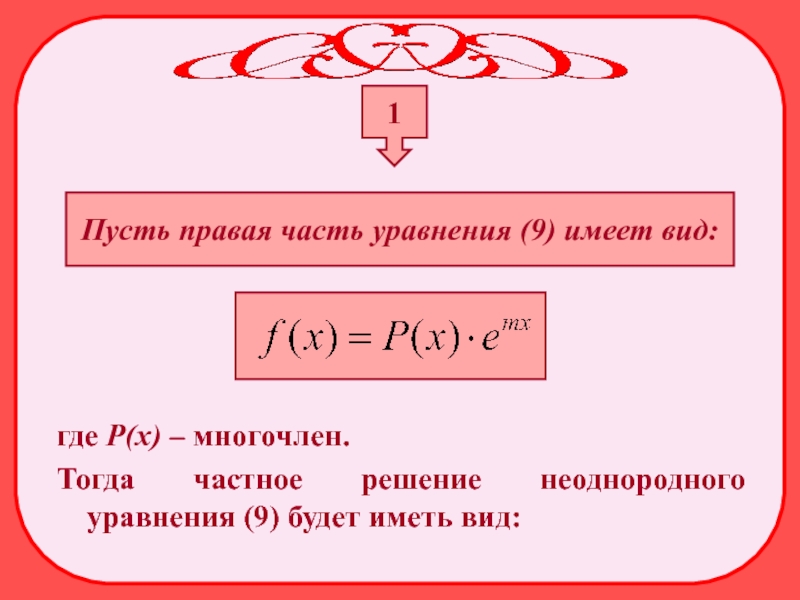
- 25. 1 Пусть правая часть уравнения (9) имеет
- 26. где Q(х) – многочлен той же
- 27. ПРИМЕР. Решить дифференциальное уравнение:
- 28. Решение: Корни вещественные и одинаковые, поэтому общее
- 29. Теперь решаем неоднородное уравнение. Правая часть представляет
- 30. Находим производные и подставляем в исходное уравнение: Частное решение неоднородного уравнения имеет вид:
- 31. Общее решение неоднородного уравнения запишем как сумму
- 32. 2 Пусть правая часть уравнения (9) имеет вид:
- 33. Если числа не являются корнями характеристического уравнения,
- 34. ПРИМЕР. Решить дифференциальное уравнение:
- 35. Решение: Сначала решаем однородное уравнение:
- 36. Корни комплексные, поэтому общее решение будет иметь
- 37. Находим производные и подставляем в исходное уравнение:
- 38. Частное решение неоднородного уравнения имеет вид: Общее
- 39. 3 Пусть правая часть уравнения (9) имеет
- 40. Если числа не являются корнями характеристического уравнения,
- 41. где R1(х) и R2(х) – многочлены той
Уравнение вида называется линейным ДУ с постоянными коэффициентами 9
Слайд 121.8. ЛИНЕЙНЫЕ ДУ ВТОРОГО
ПОРЯДКА С ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ
Рассмотрим случай, когда в
уравнении
Слайд 3Где у – искомая функция, p, g – постоянные величины.
Если f(х)=0,
то уравнение называется
линейным однородным.
линейным однородным.
Если f (х) не равно 0, то уравнение
называется линейным неоднородным.
Слайд 4Рассмотрим сначала однородное уравнение:
Будем искать решение этого уравнения в виде
Где k
- некоторое число.
Находим производные и подставляем в исходное уравнение:
Находим производные и подставляем в исходное уравнение:
10
Слайд 6Вид решения линейного однородного ДУ (10) существенно зависит от того, какие
корни имеет его характеристическое уравнение.
Обозначим эти корни как k1 и k2.
Обозначим эти корни как k1 и k2.
Слайд 7ТЕОРЕМА.
Если корни характеристического уравнения вещественные и разные
то общее решение однородного уравнения
(9) имеет вид:
Слайд 8
Если корни характеристического уравнения вещественные и равные
то общее решение однородного уравнения
(10) имеет вид:
Слайд 9
Если характеристическое уравнение не имеет вещественных корней, то общее решение однородного
уравнения (10) имеет вид:
где
-комплексные корни характеристического уравнения.
Слайд 16Теперь рассмотрим решение неоднородного ЛДУ с постоянными коэффициентами (9).
Общее решение неоднородного
ЛДУ
с постоянными коэффициентами
находится как сумма общего решения
однородного уравнения и какого-либо
частного решения неоднородного
уравнения.
с постоянными коэффициентами
находится как сумма общего решения
однородного уравнения и какого-либо
частного решения неоднородного
уравнения.
Слайд 19Корни вещественные и разные, поэтому общее решение будет иметь вид:
Теперь находим
частное решение неоднородного уравнения методом вариации постоянных в виде:
Слайд 23Интегрируем эти выражения:
Частное решение неоднородного уравнения имеет вид:
Общее решение будет:
Слайд 251
Пусть правая часть уравнения (9) имеет вид:
где Р(х) – многочлен.
Тогда
частное решение неоднородного уравнения (9) будет иметь вид:
Слайд 26
где Q(х) – многочлен той же степени, что и Р(х).
Причем,
если m не является корнем характеристического уравнения, то
r=0,
а если является, то r – кратность этого корня.
r=0,
а если является, то r – кратность этого корня.
Слайд 28Решение:
Корни вещественные и одинаковые, поэтому общее решение однородного уравнения будет иметь
вид:
Сначала решаем однородное уравнение:
Слайд 29Теперь решаем неоднородное уравнение. Правая часть представляет собой рассмотренный случай:
m –
не является корнем характеристического уравнения, следовательно r=0. Поэтому частное решение неоднородного уравнения будем искать в виде:
Слайд 30Находим производные и подставляем в исходное уравнение:
Частное решение неоднородного уравнения имеет
вид:
Слайд 31Общее решение неоднородного уравнения запишем как сумму общего решения однородного уравнения
и частного решения неоднородного уравнения:
Слайд 33Если числа
не являются корнями характеристического уравнения, то частное решение неоднородного уравнения
(9) будет иметь вид:
Если числа
являются корнями характеристического уравнения, то частное решение будет иметь вид:
Слайд 36Корни комплексные, поэтому общее решение будет иметь вид:
Теперь решаем неоднородное уравнение.
Правая часть представляет собой рассмотренный случай:
2i и –2i не являются корнями характеристического уравнения, следовательно частное решение неоднородного уравнения будем искать в виде:
Слайд 38Частное решение неоднородного уравнения имеет вид:
Общее решение неоднородного уравнения запишем как
сумму общего решения однородного уравнения и частного решения неоднородного уравнения:
Слайд 40Если числа
не являются корнями характеристического уравнения, то частное решение неоднородного уравнения
(9) будет иметь вид:
Если числа
являются корнями характеристического уравнения, то частное решение будет иметь вид:
