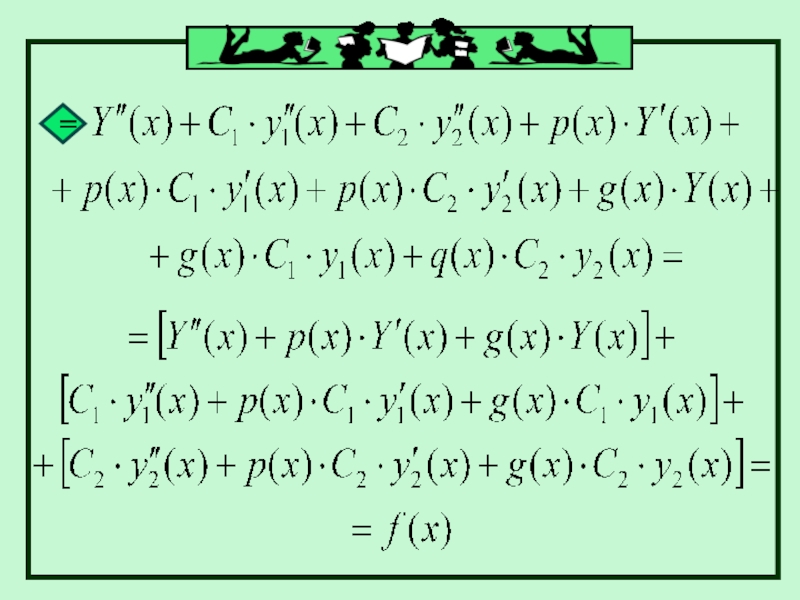- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейные ДУ второго порядка презентация
Содержание
- 1. Линейные ДУ второго порядка
- 2. Где у – искомая функция, p(x), g(x),
- 3. Если разрешить это уравнение относительно второй производной,
- 4. ЛИНЕЙНЫЕ ОДНОРОДНЫЕ ДУ ВТОРОГО ПОРЯДКА Линейным однородным
- 5. ТЕОРЕМА. Пусть функции у1(х) и у2(х)
- 6. Доказательство: Найдем первую и вторую производные от
- 7. (поскольку функции у1 (х) и у2 (х) – решения этого уравнения).
- 8. Ранее было введено понятие линейной зависимости векторов.
- 9. Линейно зависимые функции оказываются пропорциональными, т.е.
- 10. Введем для случая двух функций определитель Вронского
- 11. ТЕОРЕМА. Если функции у1 (х) и у2
- 12. Доказательство: Пусть функции у1 (х) и у2
- 13. Вторую часть теоремы докажем от противного: Пусть
- 14. ТЕОРЕМА. Пусть решения уравнения (7) у1(х)
- 15. Доказательство: Функция является решением уравнения (7). Нужно
- 16. Составим из них начальные условия: Подставим в
- 17. Определитель этой системы есть определитель Вронского. Поскольку
- 18. Подставляем эти решения в исходную функцию: Получили
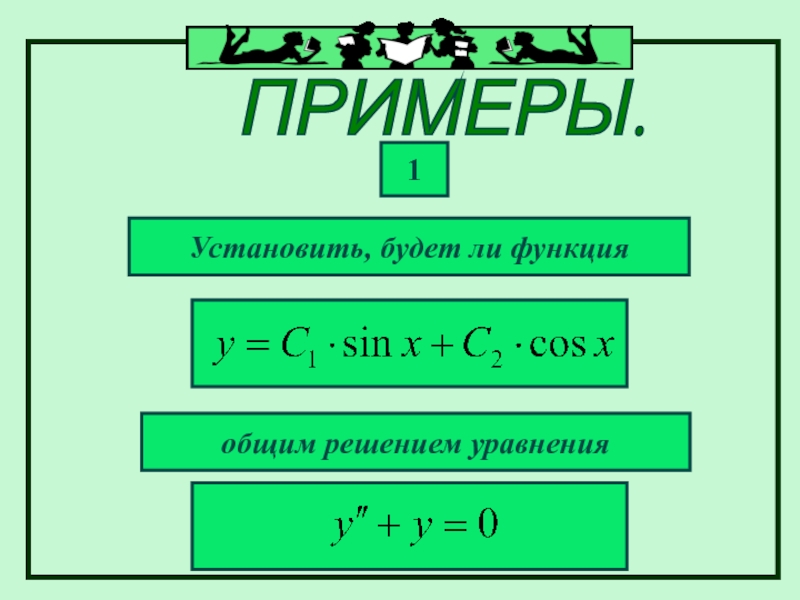
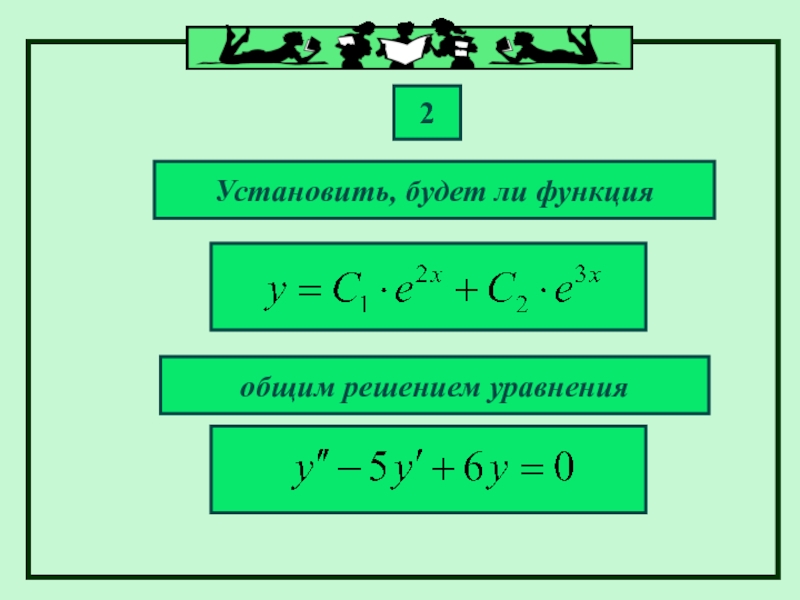
- 19. ПРИМЕРЫ. Установить, будет ли функция 1 общим решением уравнения
- 20. Решение: По теореме это решение будет общим,
- 21. Следовательно, данные функции являются решением этого
- 22. Следовательно, данные функции являются линейно независимыми. Таким образом, функция будет общим решением заданного уравнения.
- 23. Установить, будет ли функция 2 общим решением уравнения
- 24. Решение: По теореме это решение будет общим,
- 25. Следовательно, данные функции являются решением этого
- 26. Следовательно, данные функции являются линейно независимыми. Таким образом, функция будет общим решением заданного уравнения.
- 27. ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ ДУ ВТОРОГО ПОРЯДКА Линейным неоднородным
- 28. ТЕОРЕМА. Общее решение уравнения (8) состоит из
- 29. Доказательство: Пусть - общее решение соответствующего однородного
- 30. Сначала покажем, что функция является решением уравнения (8). Подставляем в уравнение (8):
- 31. = Учтем, что Тогда
- 32. =
- 33. Таким образом, функция является решением уравнения
- 34. Поскольку Подставляем в это уравнение:
- 35. Следовательно, эту разность можно записать в виде частного решения однородного уравнения (7):
- 36. Таким образом, любое решение уравнения (8) можно
- 37. Таким образом, чтобы найти общее решение
- 38. Для нахождения частного решения неоднородного уравнения используется
- 39. Тогда Дифференцируем это равенство: Положим функции
- 40. такими, что выполняется равенство: Тогда Находим вторую производную:
- 41. Подставляем найденные производные в уравнение (8): Перегруппируем слагаемые с С1(х) и С2(х) :
- 42. Так как у1(х) и у2(х) – решения
- 43. Объединим его с равенством Получаем систему:
- 44. Определитель этой системы есть определитель Вронского. Поскольку
- 45. Интегрируем эти выражения, получим Подставляем их в выражение и получаем частное решение неоднородного уравнения.
- 46. ПРИМЕР. Найти общее решение уравнения
- 47. Решение: Рассмотрим однородное уравнение: Ранее было показано,
- 48. Пусть Тогда Подставляем в уравнение:
- 49. Получаем:
- 50. Первое уравнение умножаем на 2 и вычтем
- 51. Интегрируем эти выражения:
- 52. При интегрировании можно опустить произвольные постоянные т.к.
- 53. Складываем это частное решение и общее решение однородного уравнения, получаем общее решение исходного неоднородного уравнения:
Где у – искомая функция, p(x), g(x), f(x) – функции, непрерывные на некотором интервале (a,b). Если f(x)=0, то уравнение называется линейным однородным. Если f(x) не равно 0, то уравнение называется
Слайд 1Линейным дифференциальным уравнением
второго порядка (ЛДУ) называется
уравнение вида
21.7.Линейные ДУ второго порядка
Слайд 2Где у – искомая функция, p(x), g(x), f(x) – функции, непрерывные
на некотором интервале (a,b).
Если f(x)=0, то уравнение называется
линейным однородным.
Если f(x) не равно 0, то уравнение
называется линейным неоднородным.
Слайд 3Если разрешить это уравнение относительно второй производной, то оно будет являться
частным случаем уравнения
и будет удовлетворять условиям теоремы Коши. Поэтому для любых начальных условий это уравнение имеет единственное решение задачи Коши.
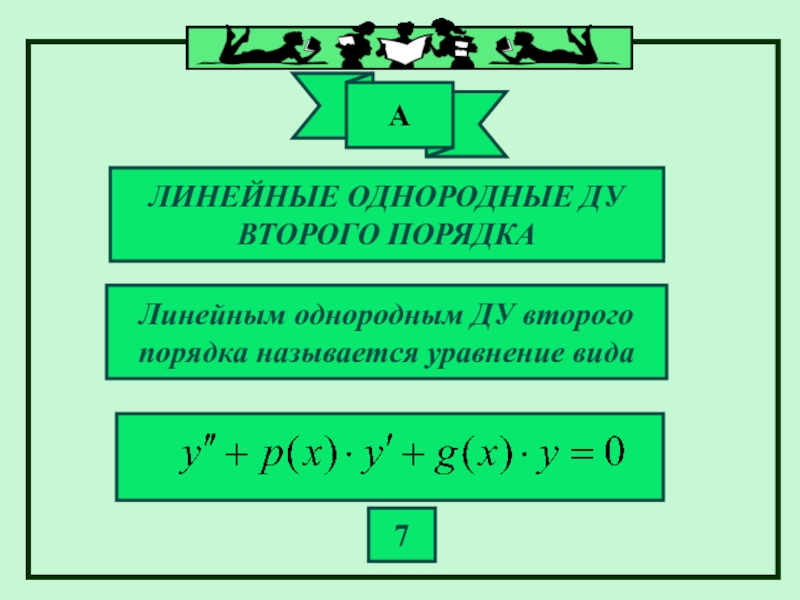
Слайд 4ЛИНЕЙНЫЕ ОДНОРОДНЫЕ ДУ
ВТОРОГО ПОРЯДКА
Линейным однородным ДУ второго
порядка называется уравнение вида
7
А
Слайд 5ТЕОРЕМА.
Пусть функции у1(х) и у2(х) – решения уравнения (7). Тогда функция
тоже будет решением этого уравнения при любых значениях постоянных С1 и С2.
Слайд 6Доказательство:
Найдем первую и вторую производные от этой функции:
и подставим их в
исходное уравнение (7):
Слайд 8Ранее было введено понятие линейной зависимости векторов. По аналогии можно ввести
понятие линейной зависимости функций.
Функции у1(х) и у2(х) называются линейно
зависимыми на интервале (а,в), если
существуют такие числа α1, α2, что для
любого х из этого интервала
выполняется равенство:
Слайд 9Линейно зависимые функции оказываются пропорциональными, т.е.
Обратное утверждение тоже верно: если
две функции пропорциональны на интервале (а,в), то они линейно зависимы на этом интервале.
Если указанное равенство не выполняется, то функции будут называться линейно независимыми.
Слайд 11ТЕОРЕМА.
Если функции у1 (х) и у2 (х) линейно зависимы
на интервале
(а,в), то определитель
Вронского, составленный из них, равен
нулю. Если же эти функции линейно
независимы, то определитель Вронского
отличен от нуля.
Вронского, составленный из них, равен
нулю. Если же эти функции линейно
независимы, то определитель Вронского
отличен от нуля.
Слайд 12Доказательство:
Пусть функции у1 (х) и у2 (х) линейно зависимы на интервале
(а,в). Тогда они будут пропорциональны, т.е.
Следовательно
Слайд 13Вторую часть теоремы докажем от противного: Пусть функции у1 (х) и
у2 (х) линейно независимы на интервале (а,в). Предположим, что
Тогда его столбцы будут пропорциональны, следовательно, пропорциональны сами функции, и тогда функции должны быть линейно зависимы, что противоречит условию теоремы.
Таким образом, если функции линейно независимы, то определитель Вронского отличен от нуля.
Слайд 14ТЕОРЕМА.
Пусть решения уравнения (7) у1(х) и у2(х) – линейно независимы на
(а,в), тогда функция
где С1 и С2 – произвольные постоянные, является общим решением этого уравнения.
Слайд 15Доказательство:
Функция
является решением уравнения (7). Нужно показать, что она представляет собой общее
решение, т.е. что из нее можно выделить частное решение, удовлетворяющее любым начальным условиям.
Выберем любые числа
Выберем любые числа
Слайд 16Составим из них начальные условия:
Подставим в левую часть этих условий функцию
Получим систему двух линейных уравнений относительно неизвестных чисел С1 и С2:
Слайд 17Определитель этой системы
есть определитель Вронского.
Поскольку у1 и у2 – линейно независимы,
то
и система будет иметь единственное решение
Слайд 18Подставляем эти решения в исходную функцию:
Получили частное решение, удовлетворяющее произвольно выбранным
начальным условиям. Следовательно, функция
действительно является общим решением уравнения (7).
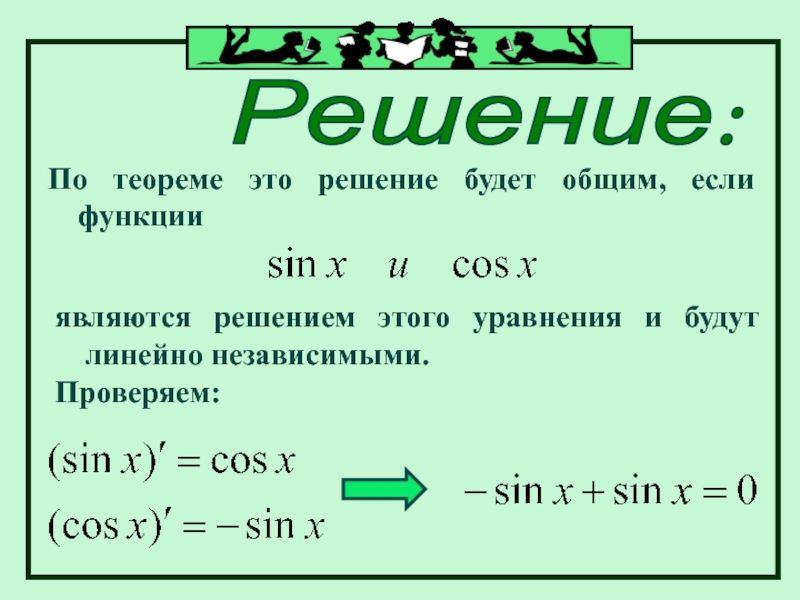
Слайд 20Решение:
По теореме это решение будет общим, если функции
являются решением этого
уравнения и будут линейно независимыми.
Проверяем:
Проверяем:
Слайд 21
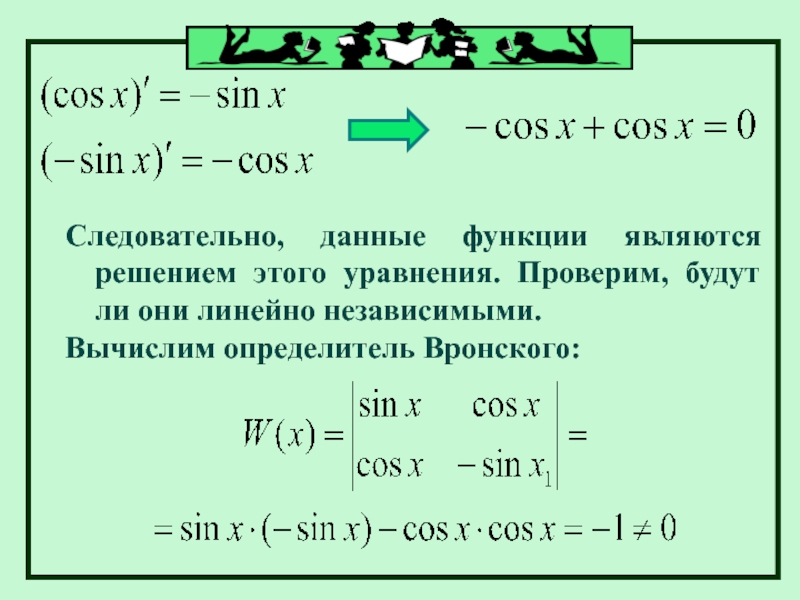
Следовательно, данные функции являются решением этого уравнения. Проверим, будут ли они
линейно независимыми.
Вычислим определитель Вронского:
Вычислим определитель Вронского:
Слайд 22Следовательно, данные функции являются линейно независимыми.
Таким образом, функция
будет общим решением заданного
уравнения.
Слайд 24Решение:
По теореме это решение будет общим, если функции
являются решением этого
уравнения и будут линейно независимыми.
Проверяем:
Проверяем:
Слайд 25
Следовательно, данные функции являются решением этого уравнения. Проверим, будут ли они
линейно независимыми.
Вычислим определитель Вронского:
Вычислим определитель Вронского:
Слайд 26Следовательно, данные функции являются линейно независимыми.
Таким образом, функция
будет общим решением заданного
уравнения.
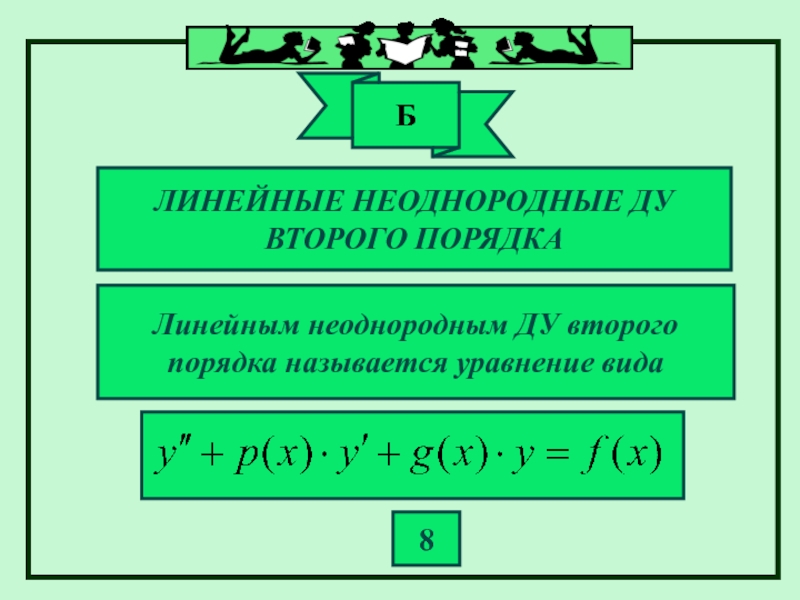
Слайд 27ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ ДУ
ВТОРОГО ПОРЯДКА
Линейным неоднородным ДУ второго
порядка называется уравнение вида
8
Б
Слайд 28ТЕОРЕМА.
Общее решение уравнения (8) состоит
из суммы его частного решения и общего
решения
соответствующего ему
однородного уравнения.
однородного уравнения.
Слайд 29Доказательство:
Пусть
- общее решение соответствующего однородного уравнения (7), и пусть
- какое-либо частное
решение неоднородного уравнения (8).
Слайд 33Таким образом, функция
является решением уравнения (8).
Теперь нужно показать, что она
является общим решением этого уравнения.
Рассмотрим разность
Рассмотрим разность
где у(х) – любое решение уравнения (8). Эта разность является решением однородного уравнения
Слайд 35Следовательно, эту разность можно записать в виде частного решения однородного уравнения
(7):
Слайд 36Таким образом, любое решение уравнения (8) можно получить по формуле:
путем подбора
произвольных постоянных
Это и означает, что данная функция является общим решением неоднородного уравнения.
Слайд 37Таким образом, чтобы найти общее
решение неоднородного уравнения (8) нужно
найти
общее решение соответствующего
однородного уравнения (7), а затем –
какое-либо частное решение неоднородного
уравнения, и эти решения сложить.
однородного уравнения (7), а затем –
какое-либо частное решение неоднородного
уравнения, и эти решения сложить.
Слайд 38Для нахождения частного решения неоднородного уравнения используется
метод вариации постоянных
Пусть
- общее решение
однородного уравнения (7). Будем считать, что частное решение неоднородного уравнения (8) имеет такой же вид, но произвольные постоянные С1 и С2 сами являются функциями от х:
Слайд 41Подставляем найденные производные в уравнение (8):
Перегруппируем слагаемые с С1(х) и С2(х)
:
Слайд 42Так как у1(х) и у2(х) – решения однородного уравнения (7), то
выражения в скобках равны нулю, следовательно:
Слайд 44Определитель этой системы
есть определитель Вронского.
Поскольку у1(х) и у2(х) – линейно независимы,
то
и система будет иметь единственное решение
Слайд 45Интегрируем эти выражения, получим
Подставляем их в выражение
и получаем частное решение
неоднородного уравнения.
Слайд 47Решение:
Рассмотрим однородное уравнение:
Ранее было показано, что его общее решение
Следовательно, частное решение
неоднородного уравнения будем искать в виде:
Слайд 50Первое уравнение умножаем на 2 и вычтем его из второго:
Теперь
подставляем в первое уравнение:
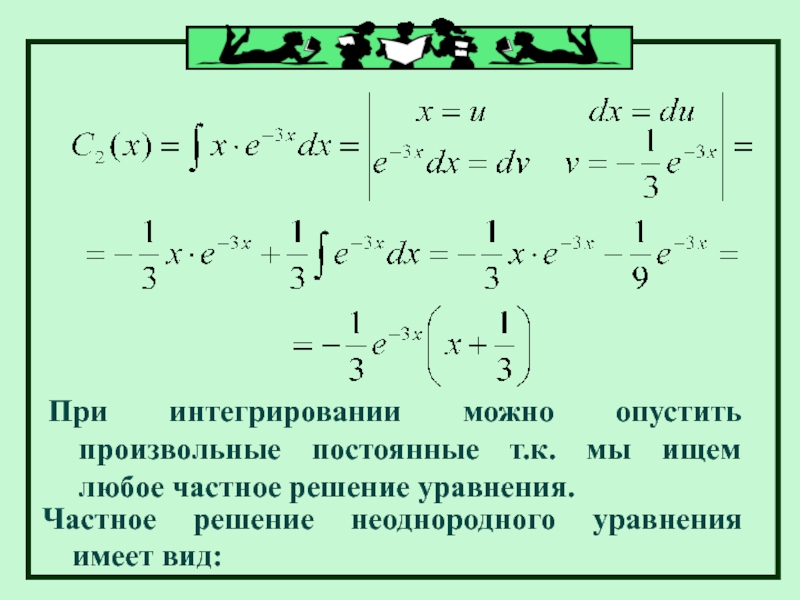
Слайд 52При интегрировании можно опустить произвольные постоянные т.к. мы ищем любое частное
решение уравнения.
Частное решение неоднородного уравнения имеет вид:
Слайд 53Складываем это частное решение и общее решение однородного уравнения, получаем общее
решение исходного неоднородного уравнения:
