- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейная регрессия презентация
Содержание
- 1. Линейная регрессия
- 2. Цели Зачем проводить регрессионный анализ
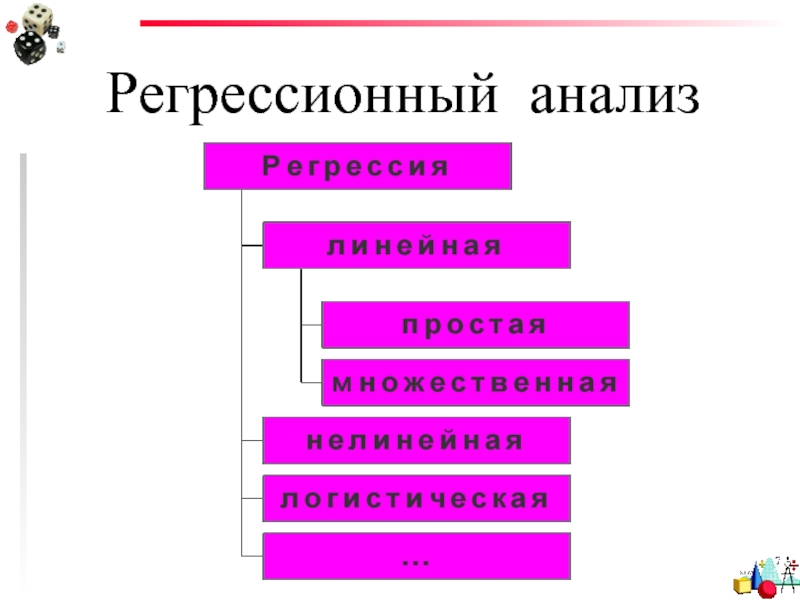
- 3. Регрессионный анализ
- 4. Регрессионный анализ служит для определения вида связи
- 5. «Регрессионный анализ является мощным средством прогноза. Экономисты,
- 6. Регрессионный анализ
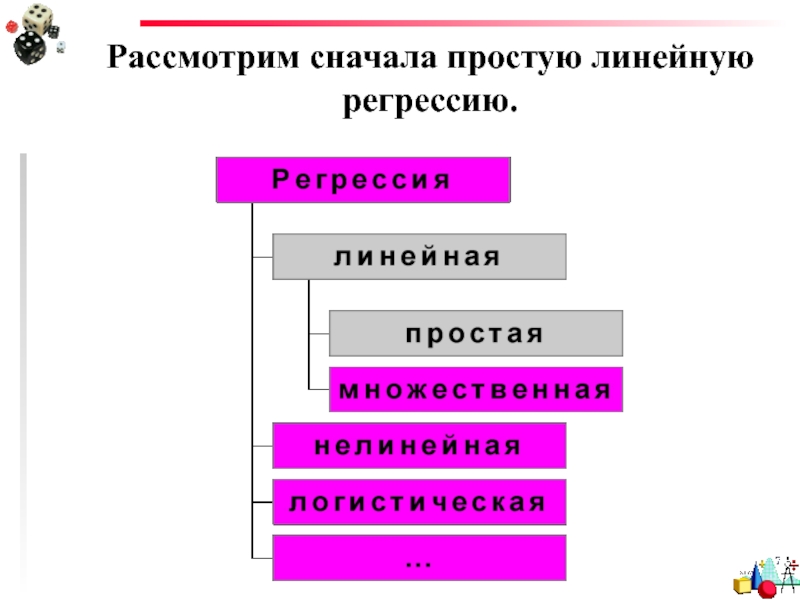
- 7. Рассмотрим сначала простую линейную регрессию.
- 8. Ограничения В случае простой линейной регрессии предполагается,
- 9. Пример 1: на диаграмме рассеяния показана зависимость
- 10. Коэффициенты a и b вычисляются по формулам:
- 11. Равенство значения коэффициента регрессии нулю говорит
- 12. Качество уравнения простой регрессии, его объясняющая способность
- 13. Уравнение простой линейной регрессии можно получить при
- 14. Уравнение регрессионной прямой и коэффициент корреляции
- 15. Для нашего примера 1 b=0,849; a=36,393
- 16. Доктор, у меня холестерин 310...
- 17. Это было просто! Ерунда для первого курса!
- 18. Модуль линейной регрессии Уравнение простой линейной регрессии
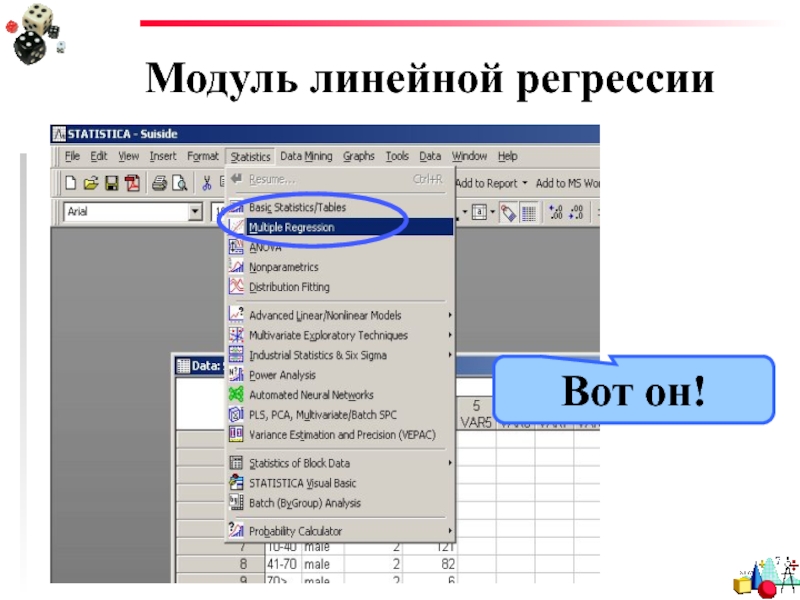
- 19. Модуль линейной регрессии Вот он!
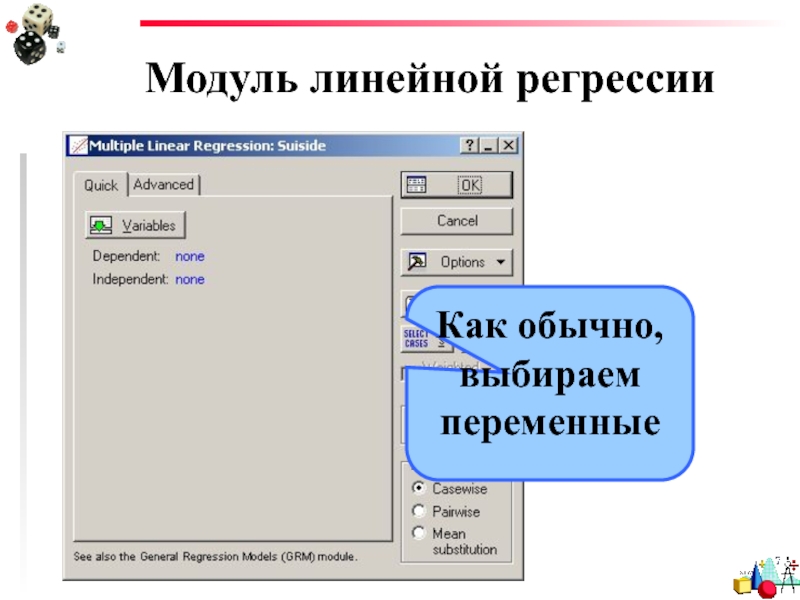
- 20. Модуль линейной регрессии Как обычно, выбираем переменные
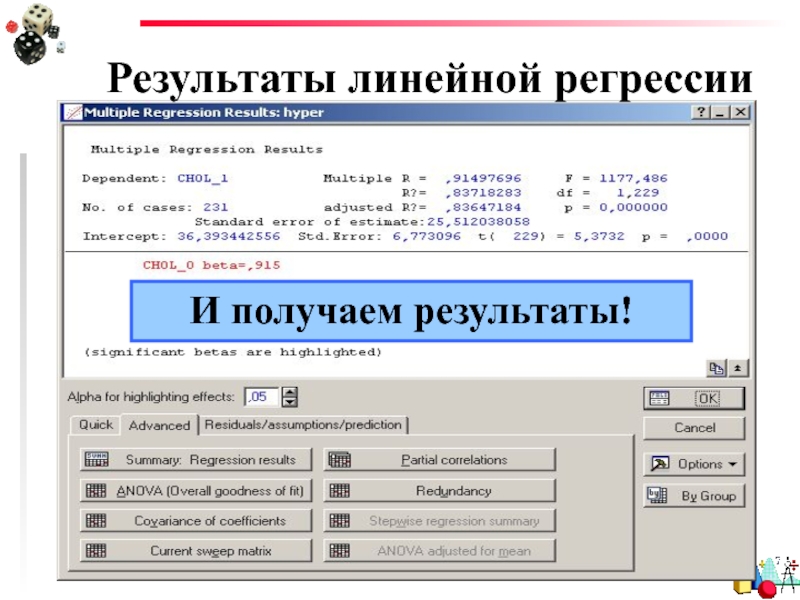
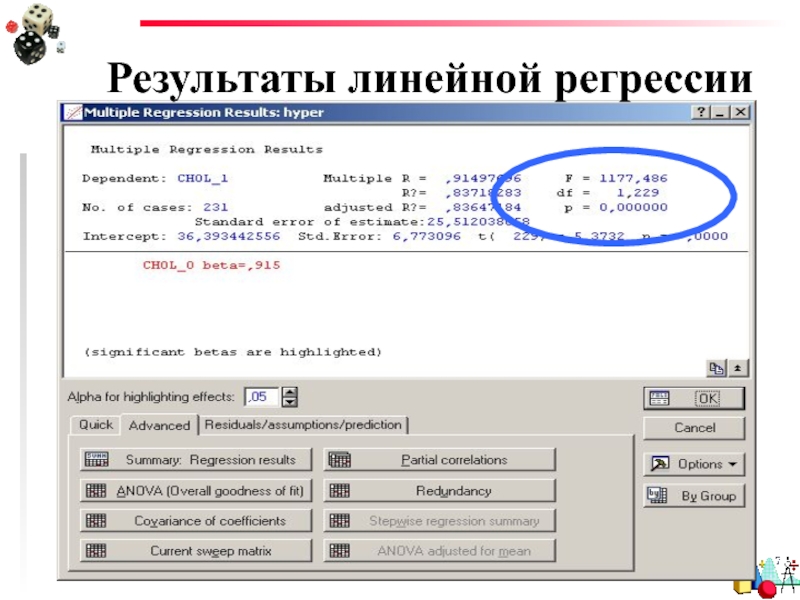
- 21. Результаты линейной регрессии И получаем результаты!
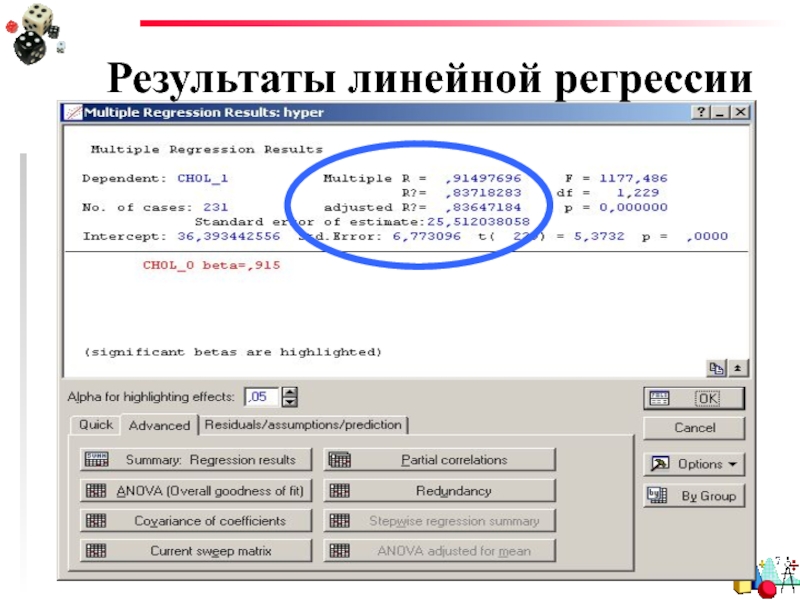
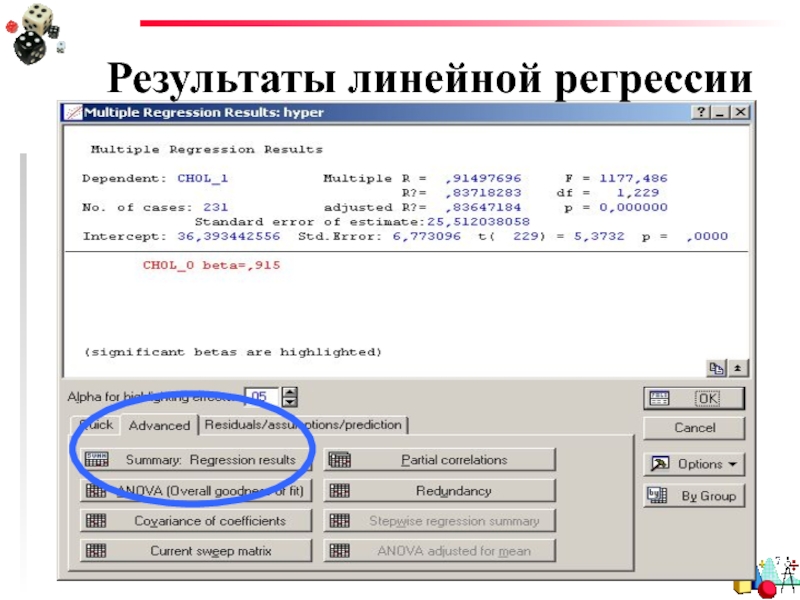
- 22. Результаты линейной регрессии
- 23. Результаты линейной регрессии
- 24. Результаты линейной регрессии
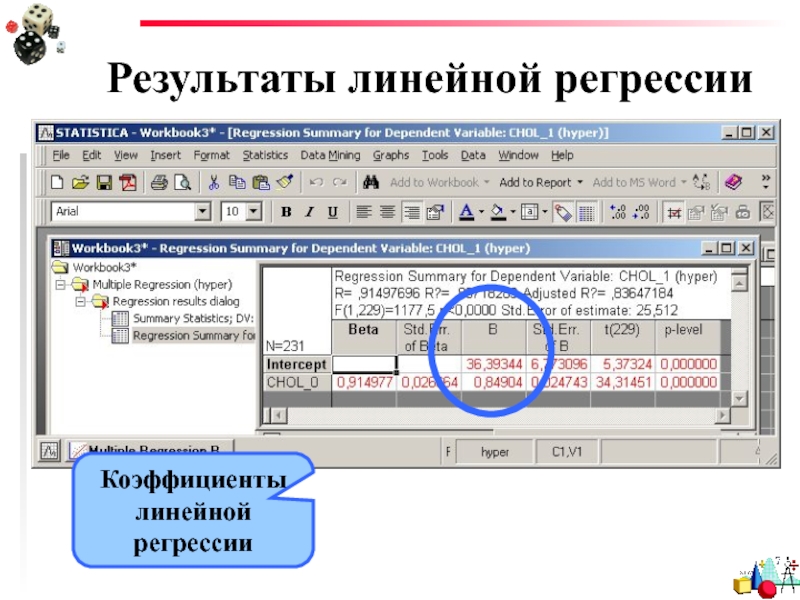
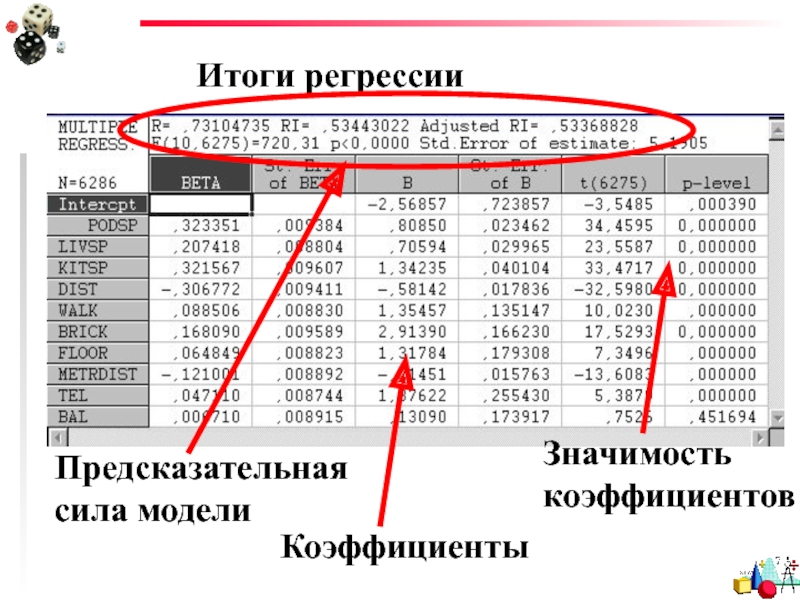
- 25. Результаты линейной регрессии Коэффициенты линейной регрессии
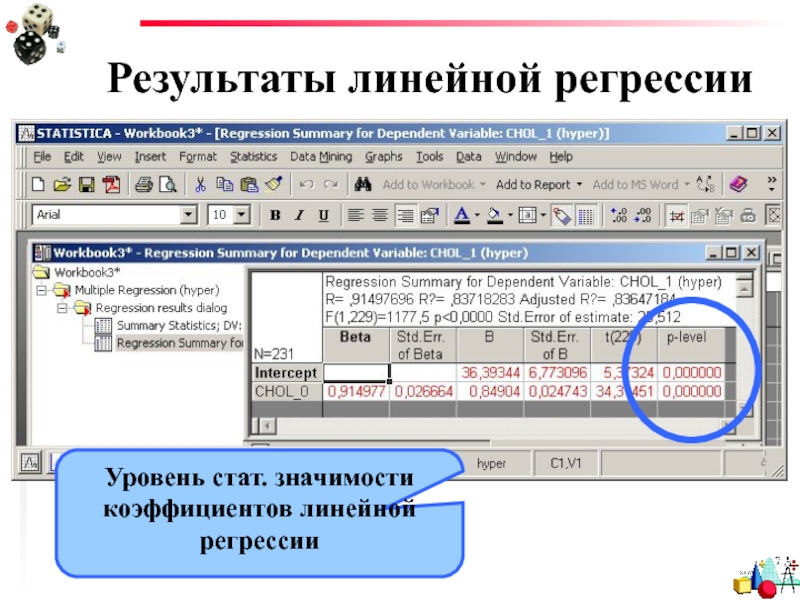
- 26. Результаты линейной регрессии Уровень стат. значимости коэффициентов линейной регрессии
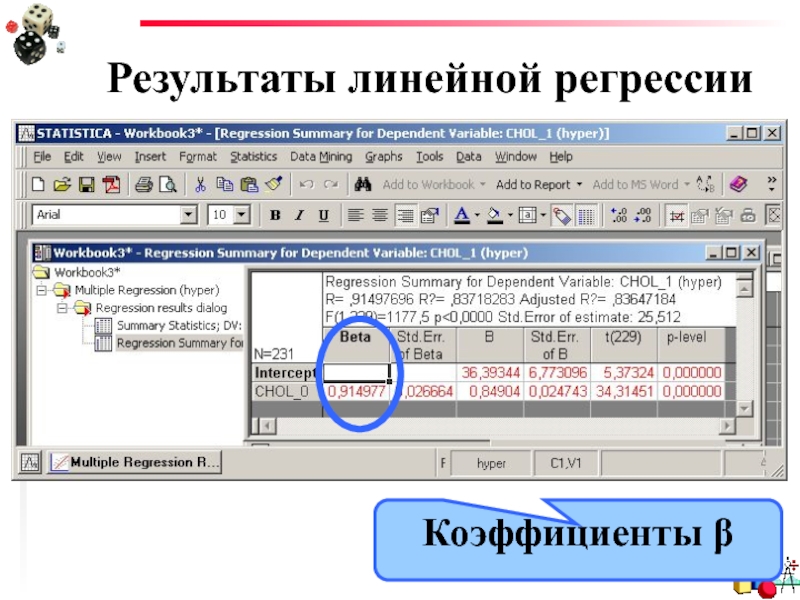
- 27. Результаты линейной регрессии Коэффициенты β
- 28. Результаты линейной регрессии Коэффициенты β - это
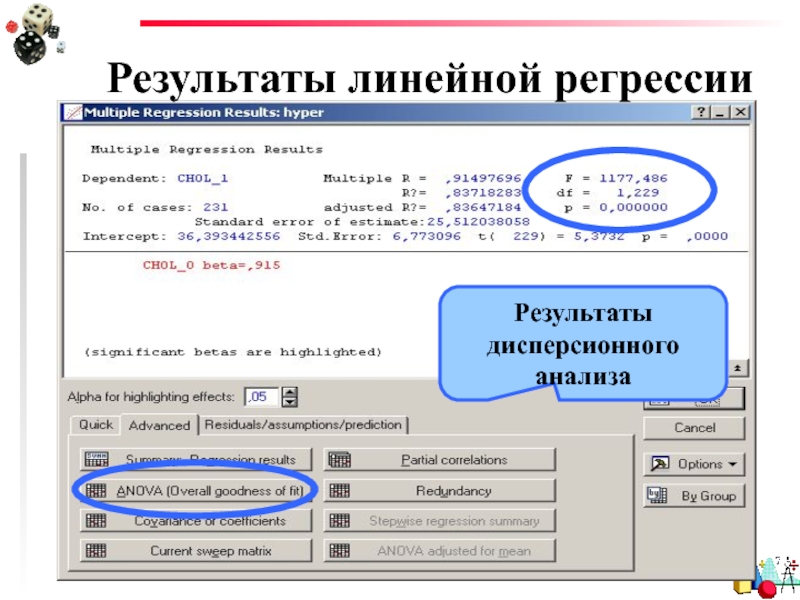
- 29. Результаты линейной регрессии Результаты дисперсионного анализа
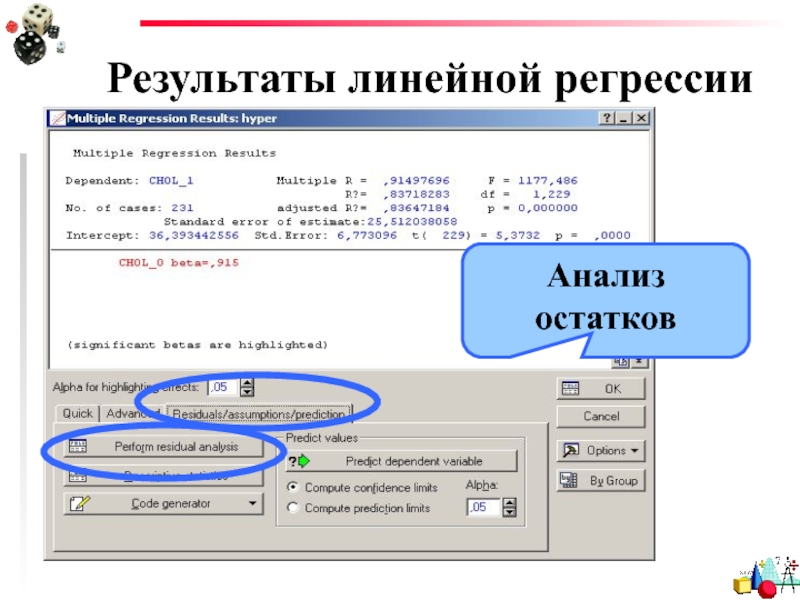
- 30. Результаты линейной регрессии Анализ остатков
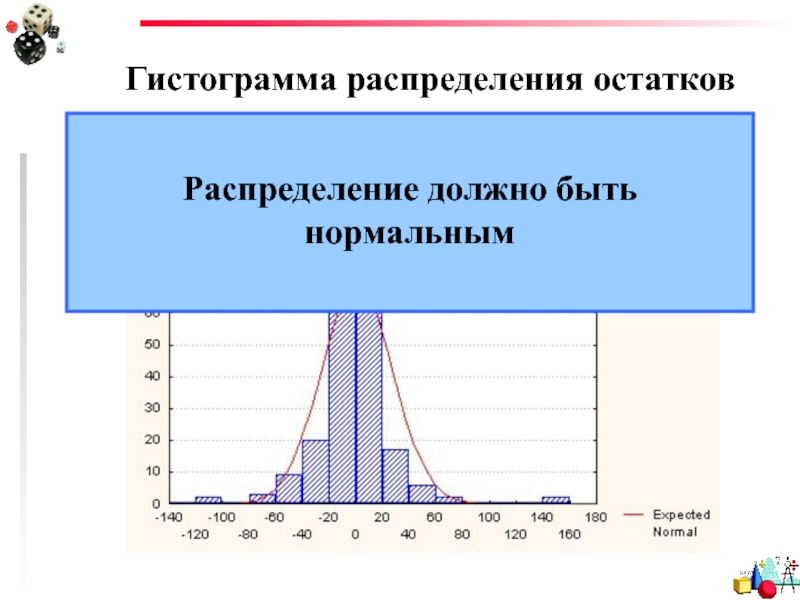
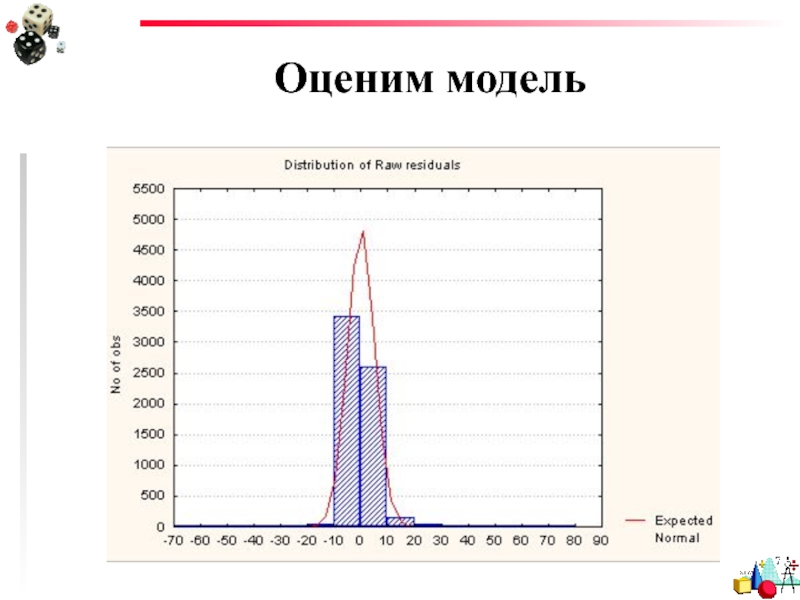
- 31. Анализ остатков Гистограмма распределения остатков
- 32. Гистограмма распределения остатков Распределение должно быть нормальным
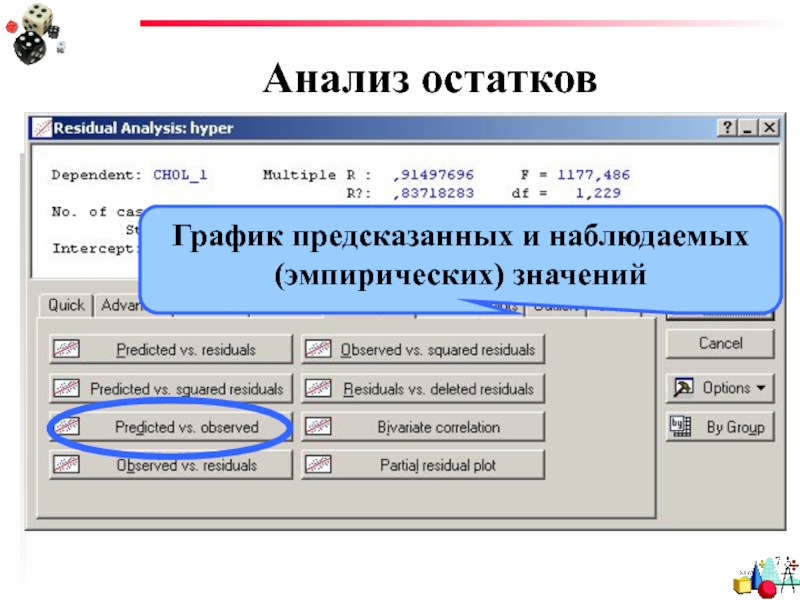
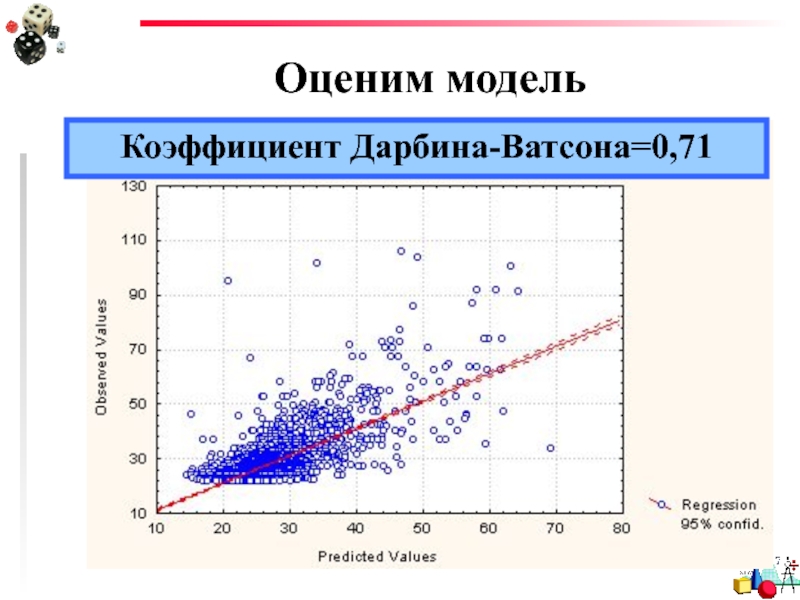
- 33. Анализ остатков График предсказанных и наблюдаемых (эмпирических) значений
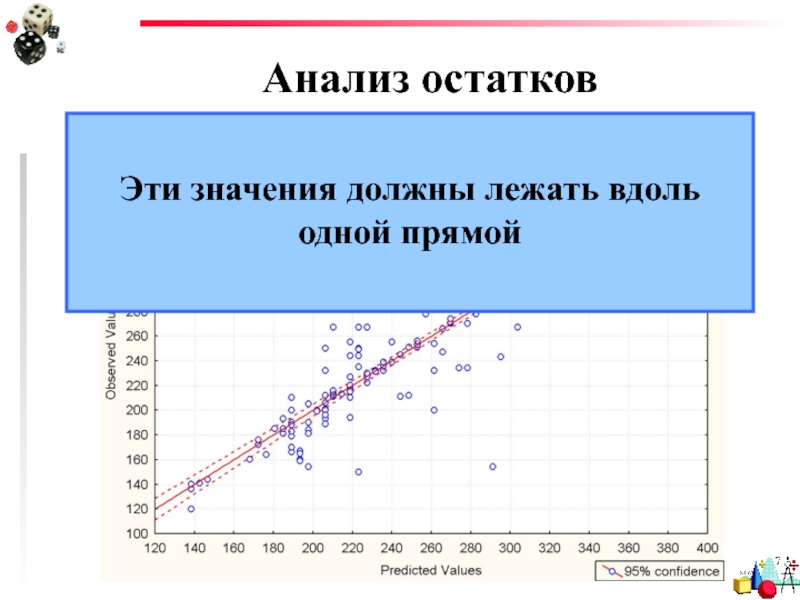
- 34. Анализ остатков Эти значения должны лежать вдоль одной прямой
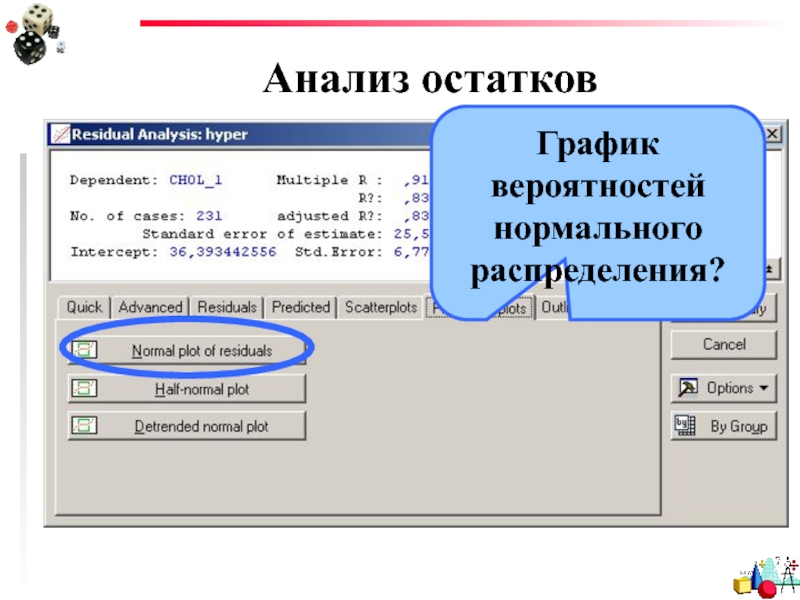
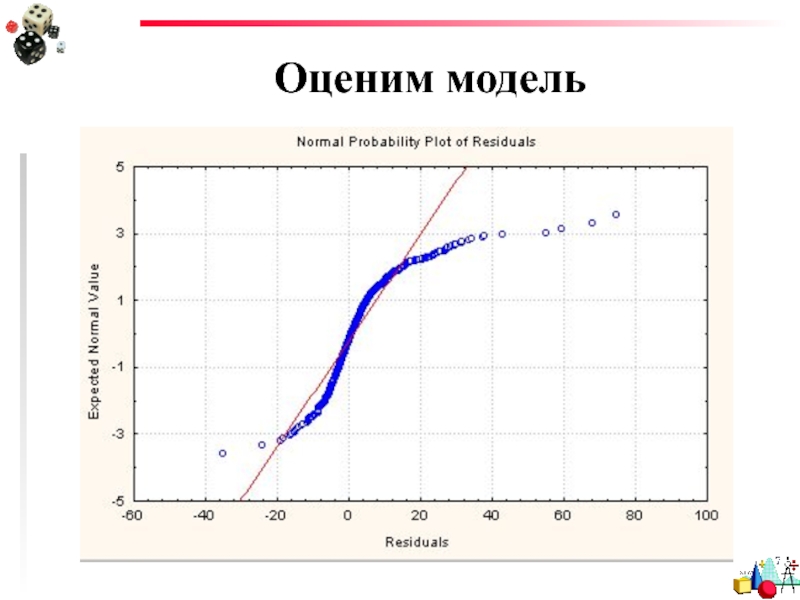
- 35. Анализ остатков График вероятностей нормального распределения?
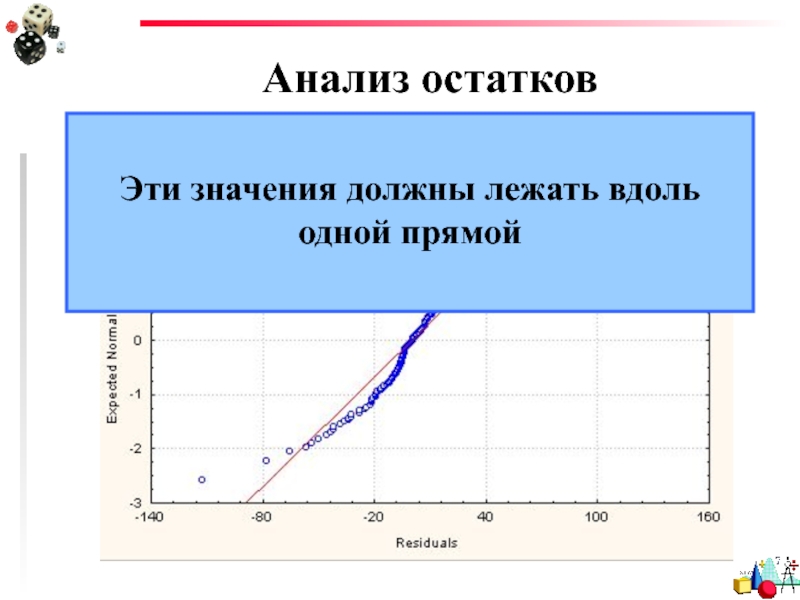
- 36. Анализ остатков Эти значения должны лежать вдоль одной прямой
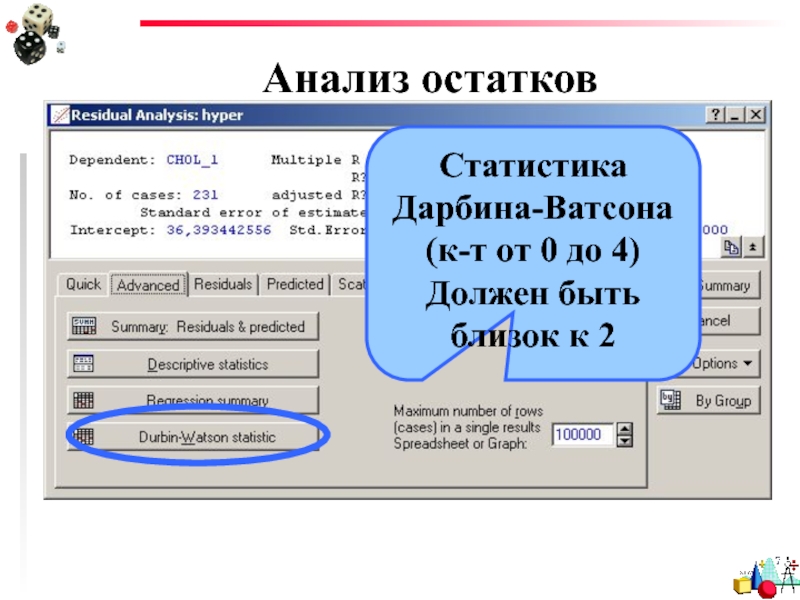
- 37. Анализ остатков Статистика Дарбина-Ватсона (к-т от 0 до 4) Должен быть близок к 2
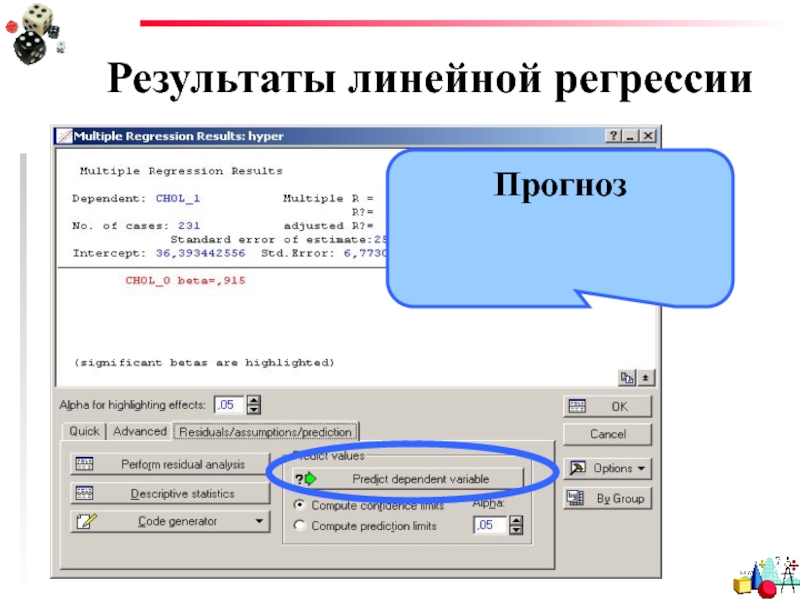
- 38. Результаты линейной регрессии Прогноз
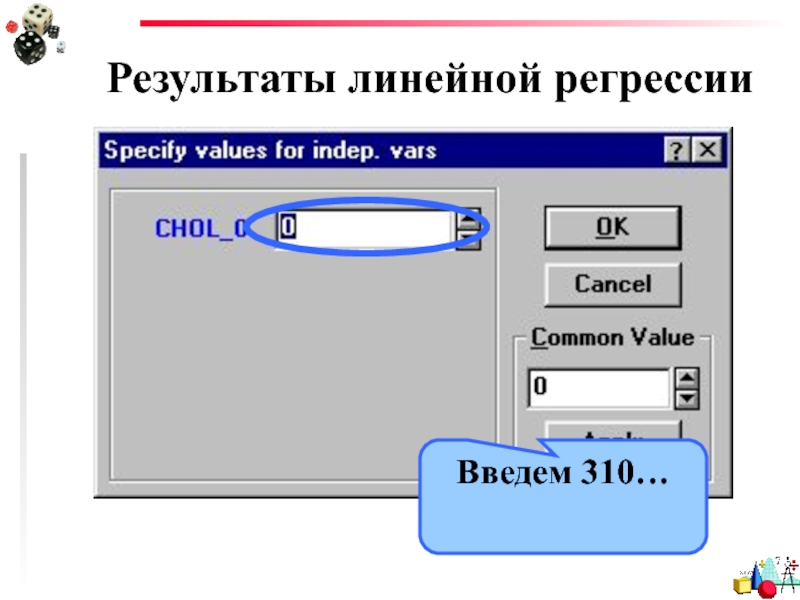
- 39. Результаты линейной регрессии Введем 310…
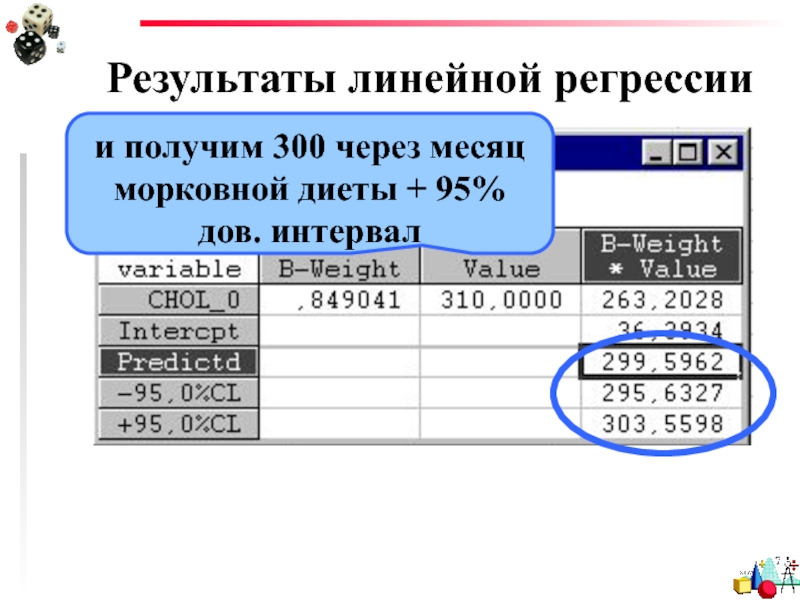
- 40. Результаты линейной регрессии и получим 300 через месяц морковной диеты + 95% дов. интервал
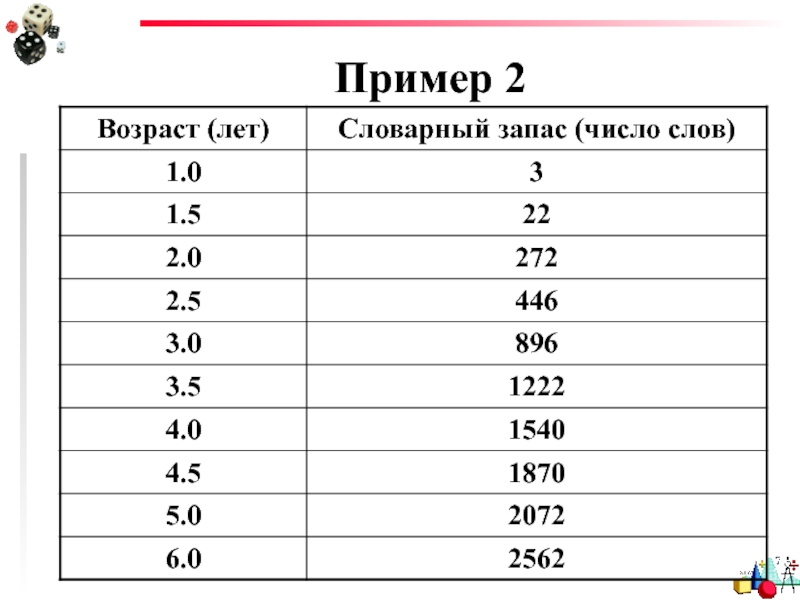
- 41. Пример 2
- 42. Пример 2 Словарный запас = 562*возраст –
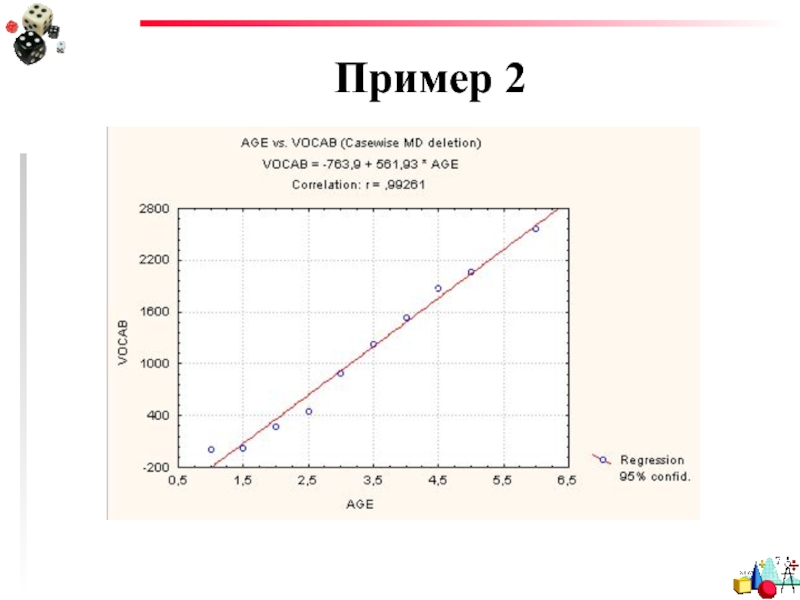
- 43. Пример 2
- 44. Пример 2 А что было, когда ребенок
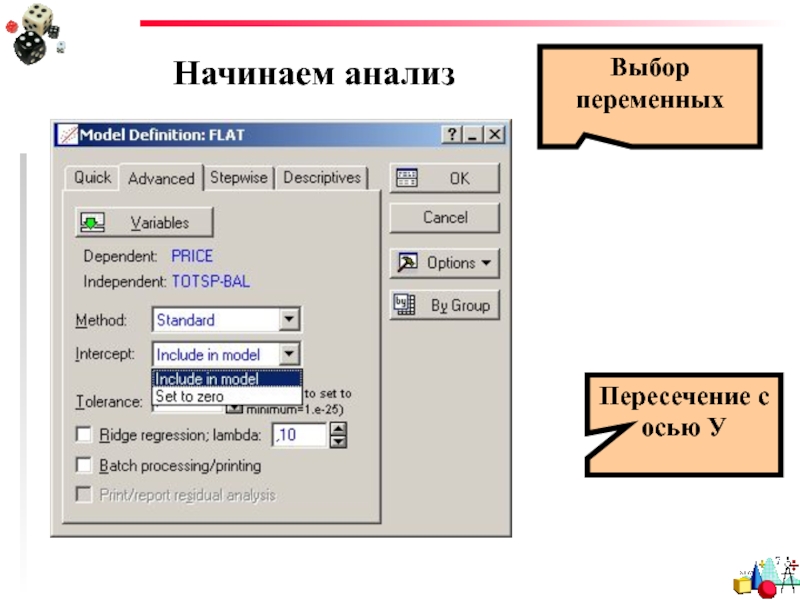
- 45. Пример 2 В этом окне можно установить смещение=0: intercept: set to zero
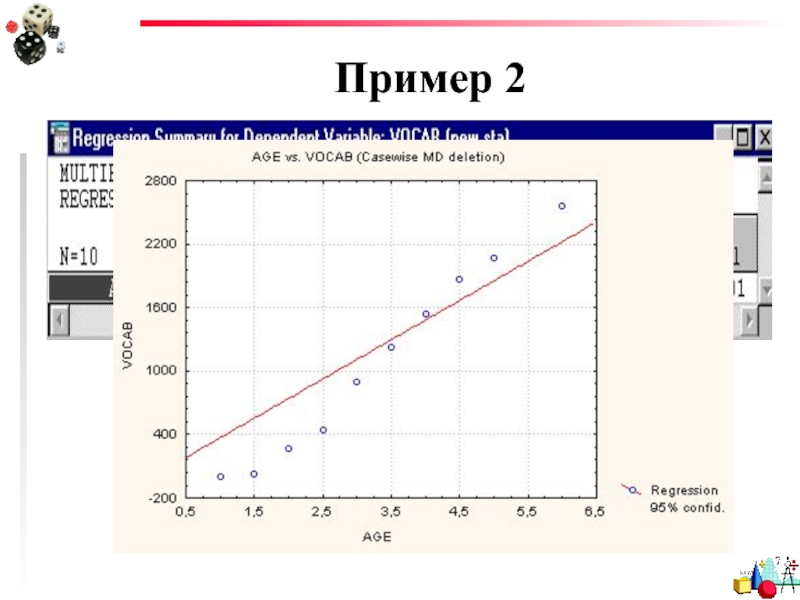
- 46. Пример 2
- 47. Фух! Достаточно про простую линейную регрессию!
- 48. Бывает, что действие зависимой переменной не может
- 49. Уравнение множественной регрессии очень похоже на уравнение
- 50. Наша задача заключается в определении коэффициентов bi и a
- 51. Ограничения В случае множественной линейной регрессии предполагается,
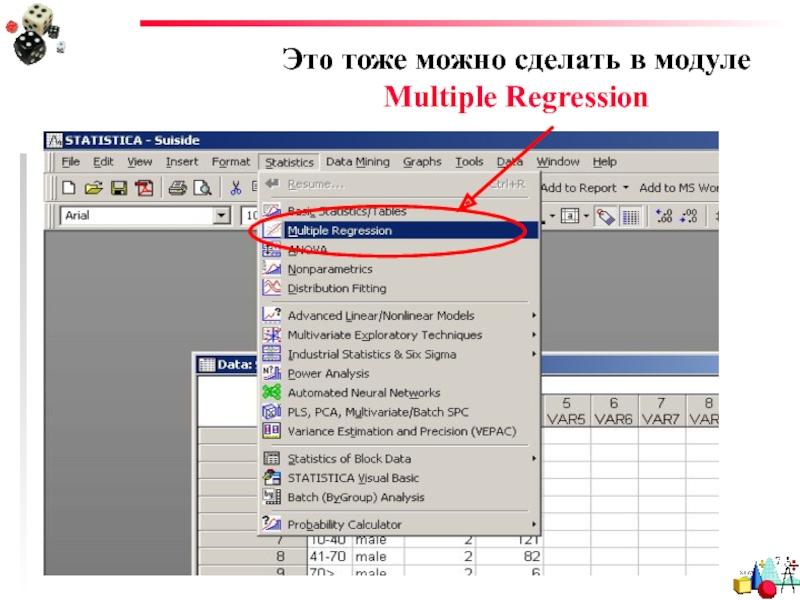
- 52. Это тоже можно сделать в модуле Multiple Regression
- 53. Рассматривались данные по двухкомнатным квартирам Число
- 54. Информация по каждой квартире: Цена квартиры
- 55. Информация по каждой квартире: Тип постройки здания
- 56. Переменные регрессионного анализа В приведенной базе данных
- 57. Задачи исследования Провести анализ влияния
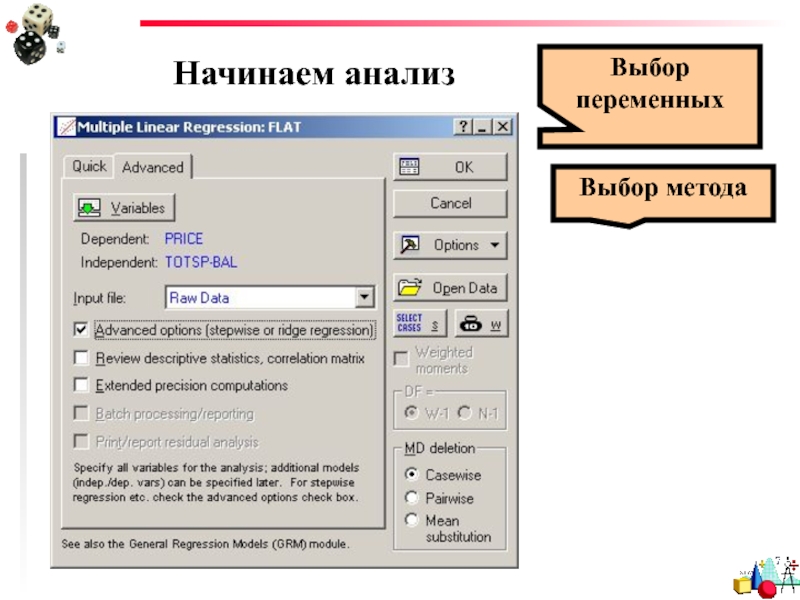
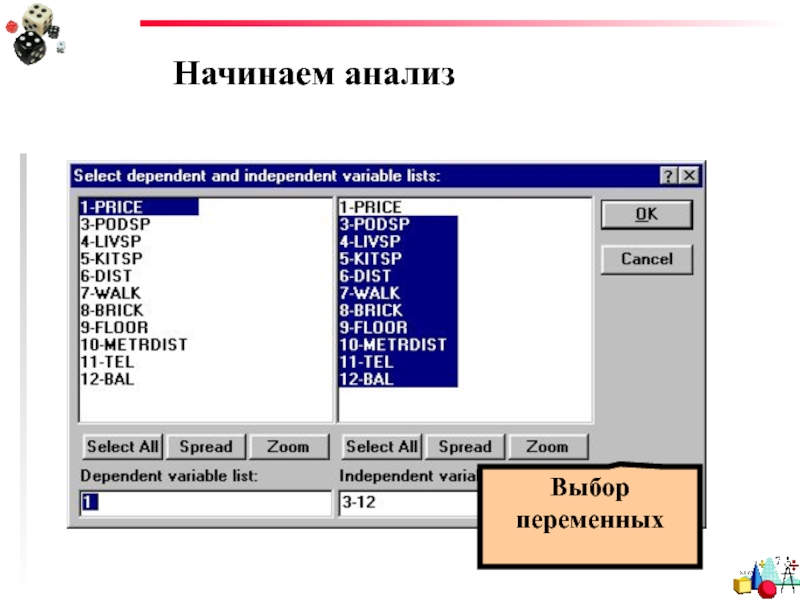
- 58. Начинаем анализ Выбор переменных Выбор метода
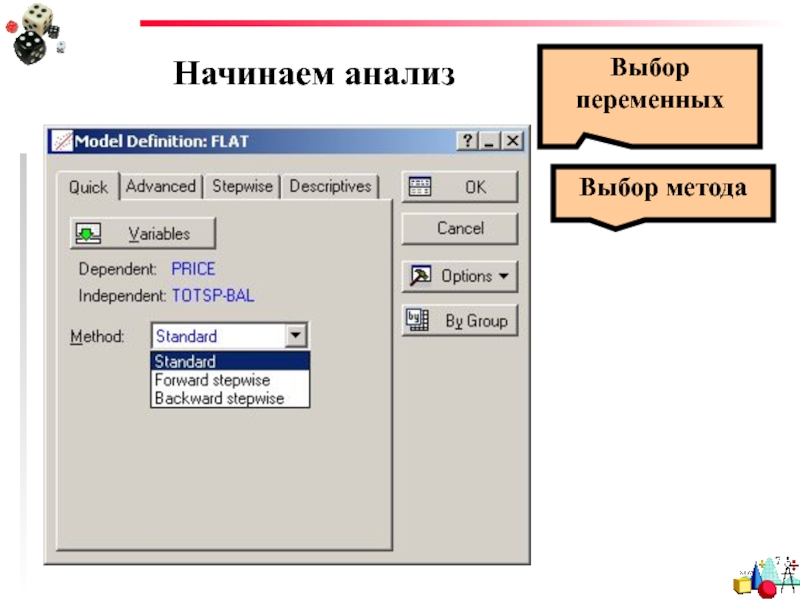
- 59. Начинаем анализ Выбор переменных Выбор метода
- 60. Начинаем анализ Выбор переменных Пересечение с осью У
- 61. Начинаем анализ Выбор переменных
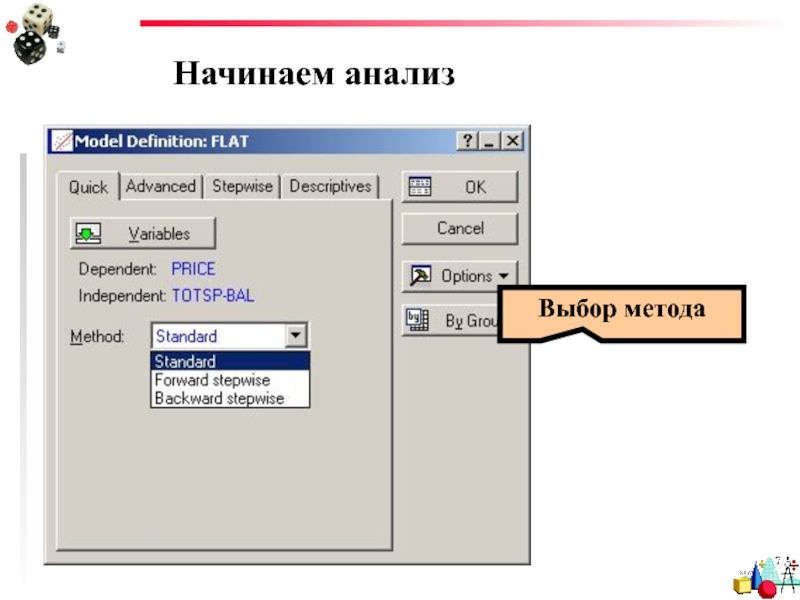
- 62. Начинаем анализ Выбор метода
- 63. Выбор метода В множественной линейной регрессии обычно
- 64. Выбор метода Standard – Стандартный – включает в анализ сразу все «независимые» переменные
- 65. Выбор метода Forward stepwise – Прямой пошаговый
- 66. Выбор метода Backward stepwise – обратный пошаговый
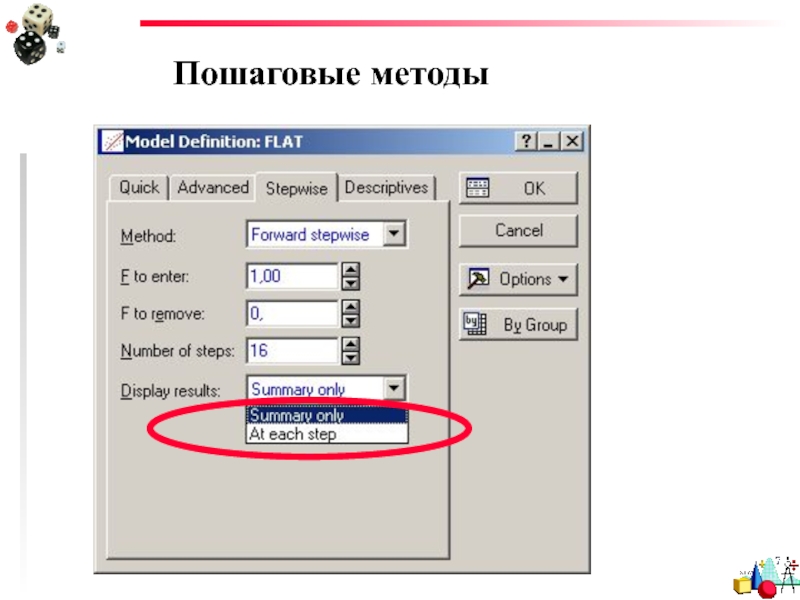
- 67. Пошаговые методы
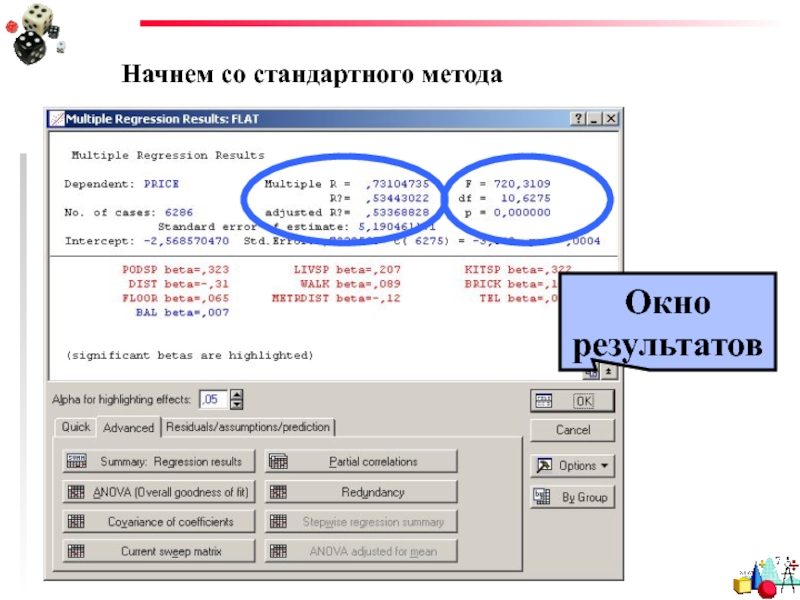
- 68. Начнем со стандартного метода Окно результатов
- 69. Итоги регрессии Предсказательная сила модели
- 70. Переменная Bal (наличие балкона) оказалась статистически незначима,
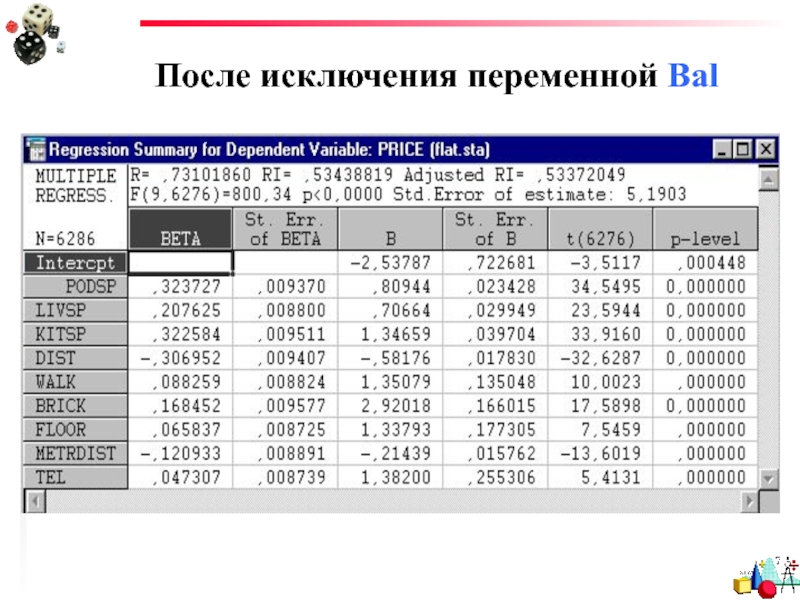
- 71. После исключения переменной Bal
- 72. Теперь можно определить стоимость квартиры: Стоимость квартиры
- 73. Оценим модель
- 74. Оценим модель
- 75. Оценим модель Коэффициент Дарбина-Ватсона=0,71
- 76. Интерпретация результатов На основе коэффициентов модели можно
- 77. Интерпретация результатов Тот факт, что тип
- 78. Интерпретация результатов А.Д. Наследов (с.243): «… знак
- 79. Пример 4 (реальные данные) ЗП: ВР НП:
- 80. Пример 4 НП Представляемость,
- 81. Пример 4 Корреляция между «знакомостью» и временем называния для трех групп:
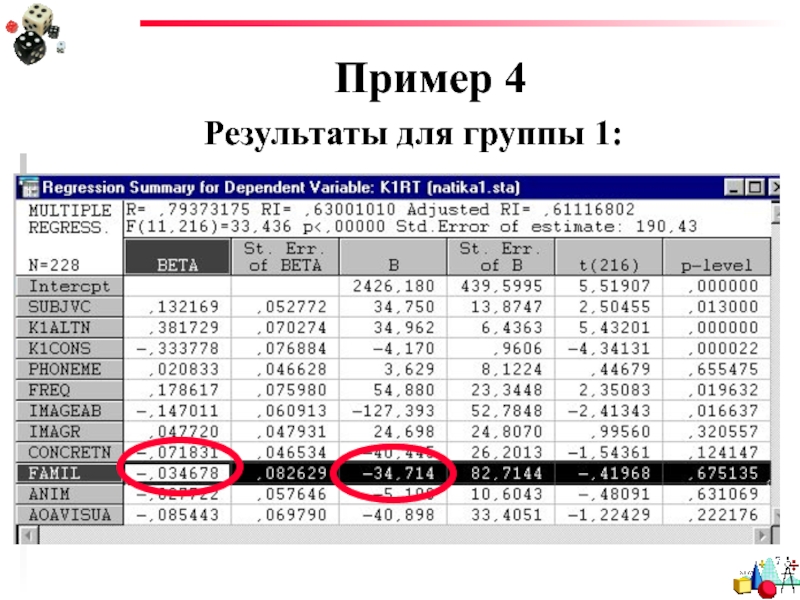
- 82. Пример 4 Результаты для группы 1:
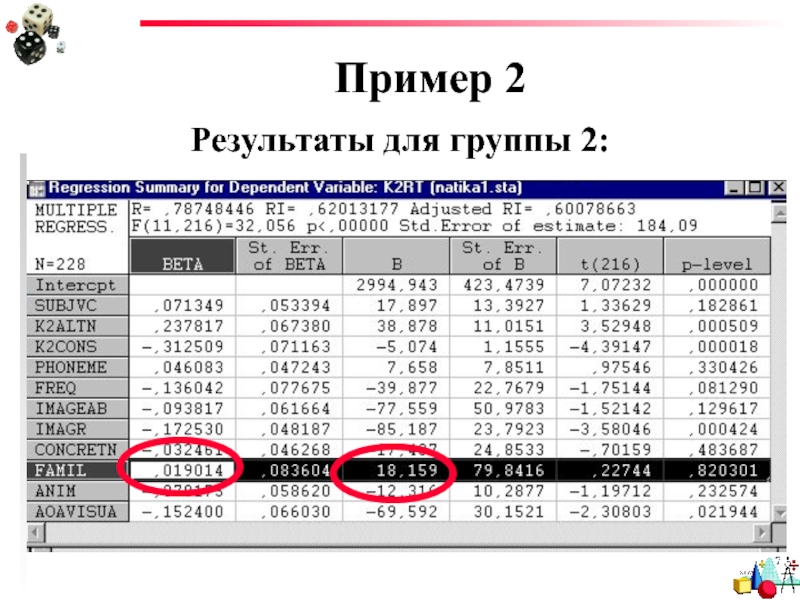
- 83. Пример 2 Результаты для группы 2:
- 84. И что же делать?!!
- 85. Будь бдительным! Так смело можно интерпретировать регрессионные
- 86. Будь бдительным! Для проверки возможных связей между
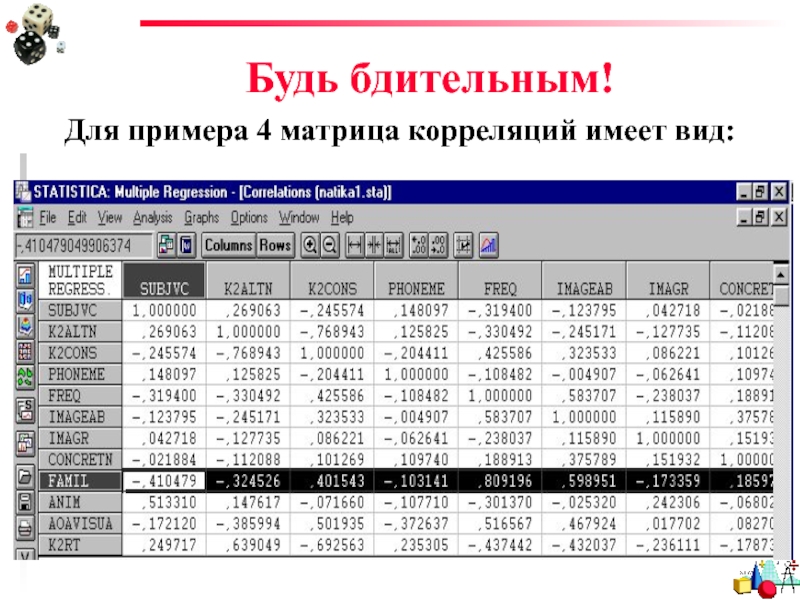
- 87. Будь бдительным! Для примера 4 матрица корреляций имеет вид:
- 88. Будь бдительным! Для проверки возможных связей между
- 89. Будь бдительным! Для проверки возможных связей между
- 90. Будь бдительным! Проверяйте наличие корреляций между независимыми переменными и используйте пошаговые методы множественной линейной регрессии
- 91. Шкалы наименований В примере 3 использовались дихотомические
- 92. Шкалы наименований Если есть шкала «профессия» с
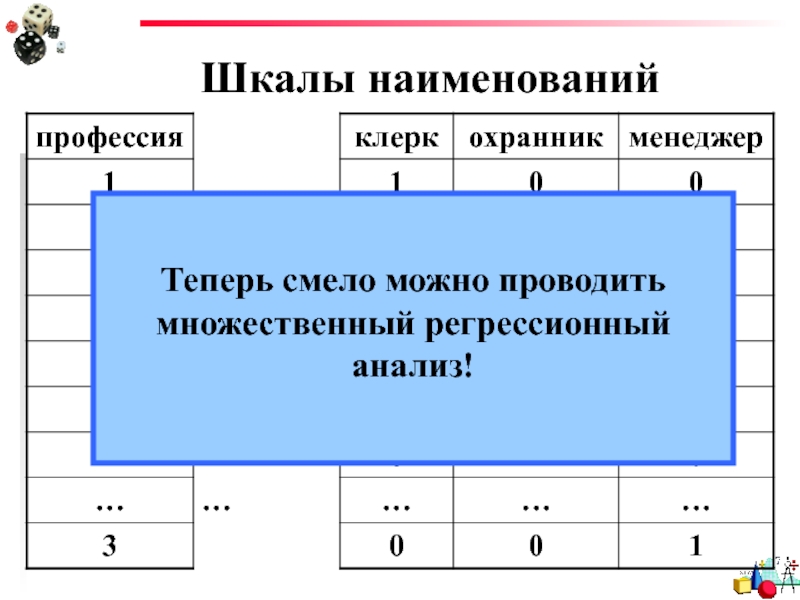
- 93. Шкалы наименований Теперь смело можно проводить множественный регрессионный анализ!
- 94. Мне кажется, Вы уже достаточно регрессировали…
- 95. К практическому занятию по регрессионному анализу надо
- 96. А что делать, если зависимая переменная не количественная, а качественная? Можно променять ДИСКРИМИНАНТНЫЙ АНАЛИЗ!
- 97. СПАСИБО ЗА ВНИМАНИЕ!
Цели Зачем проводить регрессионный анализ Как проводить регрессионный анализ Как интерпретировать результаты регрессионного анализа
Слайд 2Цели
Зачем проводить регрессионный анализ
Как проводить регрессионный анализ
Как интерпретировать
результаты регрессионного анализа
Слайд 4Регрессионный анализ служит для определения вида связи между переменными и дает
возможность для прогнозирования значения одной (зависимой) переменной, отталкиваясь от значений других (независимых) переменных.
Слайд 5«Регрессионный анализ является мощным средством прогноза. Экономисты, которые им пользовались, успешно
предсказали 10 кризисов из 2-х последних»
Материалы Интернета
Слайд 8Ограничения
В случае простой линейной регрессии предполагается, что
зависимая переменная одна и
представлена по крайней мере в интервальной шкале
независимая переменная одна и представлена по крайней мере в интервальной шкале
независимая переменная одна и представлена по крайней мере в интервальной шкале
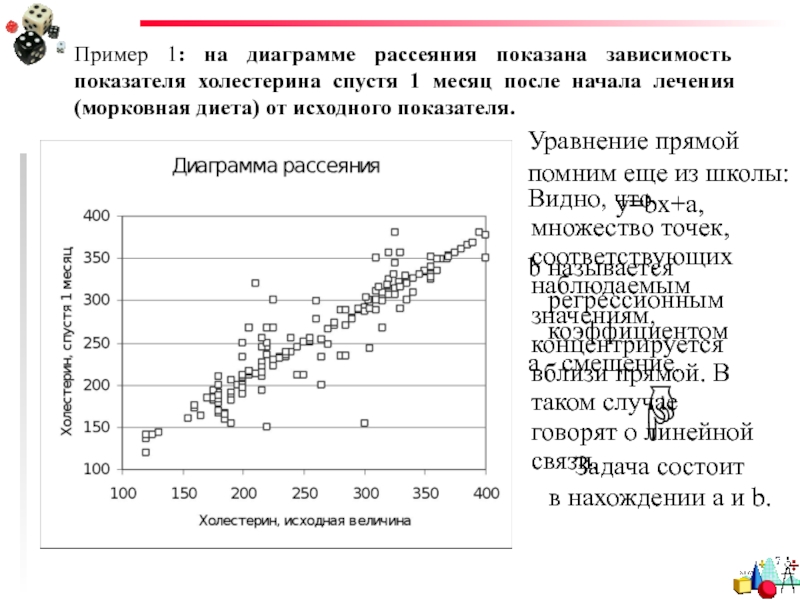
Слайд 9Пример 1: на диаграмме рассеяния показана зависимость показателя холестерина спустя 1
месяц после начала лечения (морковная диета) от исходного показателя.
Видно, что множество точек, соответствующих наблюдаемым значениям, концентрируется вблизи прямой. В таком случае говорят о линейной связи.
Уравнение прямой помним еще из школы:
y=bx+a,
b называется
регрессионным
коэффициентом
a - смещение.
☟
Задача состоит
в нахождении a и b.
Слайд 10Коэффициенты a и b вычисляются по формулам:
Знак коэффициента регрессии совпадает со
знаком коэффициента корреляции.
Слайд 11
Равенство значения коэффициента регрессии нулю говорит об отсутствии линейной связи.
Коэффициент регрессии
показывает, насколько, в среднем, увеличится или уменьшится значение зависимой переменной y при увеличении независимой переменной x на 1.
Слайд 12Качество уравнения простой регрессии, его объясняющая способность измеряется коэффициентом детерминации r2.
Коэффициент
детерминации показывает, какая доля дисперсии (изменчивости) переменной y объясняется влиянием независимой переменной x.
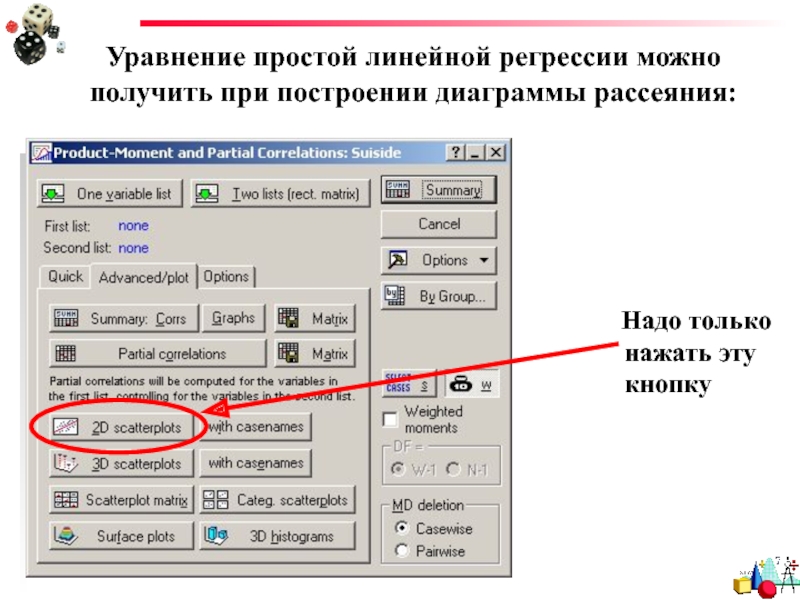
Слайд 13Уравнение простой линейной регрессии можно получить при построении диаграммы рассеяния:
Надо только нажать эту кнопку
Слайд 15Для нашего примера 1 b=0,849; a=36,393 ☟ y=0,849x+36,393 Теперь, зная, какой у вас уровень
холестерина сейчас, можно предсказать, каков он будет через месяц лечения.
Слайд 16
Доктор, у меня холестерин 310...
Ничего страшного! Через месяц морков-ной диеты у
Вас он будет уже 0,849*310+36,393=300!
Слайд 18Модуль линейной регрессии
Уравнение простой линейной регрессии можно получить и в специальном
модуле программы STATISTICA.
Он называется Multiple Regression
Он называется Multiple Regression
Слайд 28Результаты линейной регрессии
Коэффициенты β - это регрессионные коэффициенты, полученные в результате
построения регрессионной модели в случае, когда все переменные предварительно нормированы (среднее=0, станд. отклон.=1)
ПРЕИМУЩЕСТВО: позволяют определить относительный вклад каждой независимой переменной в предсказании зависимой переменной.
ПРЕИМУЩЕСТВО: позволяют определить относительный вклад каждой независимой переменной в предсказании зависимой переменной.
Слайд 44Пример 2
А что было, когда ребенок только родился?
В 0 лет словарный
запас =
= 562*возраст – 764 = -764 слова!
= 562*возраст – 764 = -764 слова!
Поэтому есть возможность установить смещение =0
Слайд 48Бывает, что действие зависимой переменной не может быть объяснено только одной
причиной (независимой) переменной. Тогда воспользуемся услугами множественной регрессии:
Слайд 49Уравнение множественной регрессии очень похоже на уравнение простой линейной регрессии:
Y=b1x1+b2x2+b3x3+ …
+ bnxn+a
bi - регрессионные коэффициенты
xi – независимые переменные, их столько, сколько вам не лень придумать или измерить
a – свободный член
bi - регрессионные коэффициенты
xi – независимые переменные, их столько, сколько вам не лень придумать или измерить
a – свободный член
Слайд 51Ограничения
В случае множественной линейной регрессии предполагается, что
зависимая переменная одна и
представлена по крайней мере в интервальной шкале
независимых переменных несколько и они представлены либо в интервальной шкале, либо в шкале равных отношений, либо в шкале наименований (!)
независимых переменных несколько и они представлены либо в интервальной шкале, либо в шкале равных отношений, либо в шкале наименований (!)
Слайд 53Рассматривались данные
по двухкомнатным квартирам
Число квартир в базе - 6286
Пример №
3
(использование множественной регрессии):
анализ данных по недвижимости
(использование множественной регрессии):
анализ данных по недвижимости
Слайд 54Информация по каждой квартире:
Цена квартиры (в тыс. $),
Общая площадь
(в м2),
Жилая площадь (в м2),
Площадь кухни (в м2),
Расстояние от центра (в км),
Способ добраться до метро
(бинарная переменная, принимающая
значение 1- пешком, 0- на транспорте).
Жилая площадь (в м2),
Площадь кухни (в м2),
Расстояние от центра (в км),
Способ добраться до метро
(бинарная переменная, принимающая
значение 1- пешком, 0- на транспорте).
Слайд 55Информация по каждой квартире:
Тип постройки здания
(бинарная переменная:
1-
кирпичный дом, 0- панельный дом)
Высота расположения квартиры
(1 - если квартира находится
не на 1 или последнем этаже,
0 - в противном случае).
Высота расположения квартиры
(1 - если квартира находится
не на 1 или последнем этаже,
0 - в противном случае).
Слайд 56Переменные регрессионного анализа
В приведенной базе данных есть дихотомические(есть-нету) (бинарные) переменные. Это
переменные, принимающие всего два значения.
Дихотомические переменные ведут себя так же, как интервальные!!!(ср.арифметическое и диссперсия).
Для них среднее арифметическое имеет смысл и можно считать к-т корреляции Пирсона!
Дихотомические переменные ведут себя так же, как интервальные!!!(ср.арифметическое и диссперсия).
Для них среднее арифметическое имеет смысл и можно считать к-т корреляции Пирсона!
Слайд 57Задачи исследования
Провести анализ влияния
характеристик квартиры
на
ее цену
Построить модель зависимости
стоимости квартиры от
исследуемых параметров и
численно оценить
коэффициенты модели a и b
Построить модель зависимости
стоимости квартиры от
исследуемых параметров и
численно оценить
коэффициенты модели a и b
Слайд 63Выбор метода
В множественной линейной регрессии обычно реализовано три метода:
Standard – Стандартный
Forward stepwise – Прямой пошаговый метод
Backward stepwise - Обратный пошаговый метод
Слайд 65Выбор метода
Forward stepwise – Прямой пошаговый метод – поочередно включает в
регрессионное уравнение каждую переменную, начиная с наиболее тесно коррелирующей с зависимой переменной до тех пор, пока р-уровень значимости коэффициента b последней из включенных переменных не превысит заданное значение
Слайд 66Выбор метода
Backward stepwise – обратный пошаговый метод – поочередно исключает переменные
из анализа, начиная с той, которая имеет наибольшее значение р-уровня значимости коэффициента b, до тех пор, пока все оставшиеся переменные не будут иметь статистически значимые b-коэффициенты
Слайд 70Переменная Bal (наличие балкона)
оказалась статистически незначима,
следовательно,
исключим ее из модели
и пересчитаем
коэффициенты
Анализ результатов
Слайд 72Теперь можно определить стоимость квартиры:
Стоимость квартиры = 751*PODSP +
+ 704*LIVSP + 1290*KITSP + +20920*DIST_1 + 1300*WALK + +3256*BRICK + 1282*FLOOR + …
Слайд 76Интерпретация результатов
На основе коэффициентов модели
можно сделать следующие выводы:
Тот факт, что быстро
добираться
до метро можно пешком, добавляет
к стоимости квартиры 1.300$.
до метро можно пешком, добавляет
к стоимости квартиры 1.300$.
Слайд 77Интерпретация результатов
Тот факт, что тип
постройки
дома кирпичный,
а не панельный,
добавляет
к стоимости
квартиры 3.200$.
…. и т.д.
квартиры 3.200$.
…. и т.д.
Слайд 78Интерпретация результатов
А.Д. Наследов (с.243):
«… знак β-коэффициента соответствует знаку коэффициента корреляции данной
«независимой» и «зависимой» переменной. Абсолютная величина β-коэффициента является максимальной – равна коэффициенту корреляции с зависимой переменной, если данная независимая переменная не коррелирует ни с одной из других независимых переменных»
Слайд 79Пример 4 (реальные данные)
ЗП: ВР
НП:
согласованность (в %)отдельно для каждой группы
Число
альтернативных названий отдельно для каждой группы
Субъективная зрительная сложность
Частота употребления слова
Субъективная зрительная сложность
Частота употребления слова
Слайд 80Пример 4
НП
Представляемость,
Конкретность,
Знакомость,
Одушевленность
Возраст, в котором слово выучено
Длина слова
(в фонемах)
Слайд 85Будь бдительным!
Так смело можно интерпретировать регрессионные к-ты только если независимые переменные
действительно независимы – не коррелируют друг с другом!
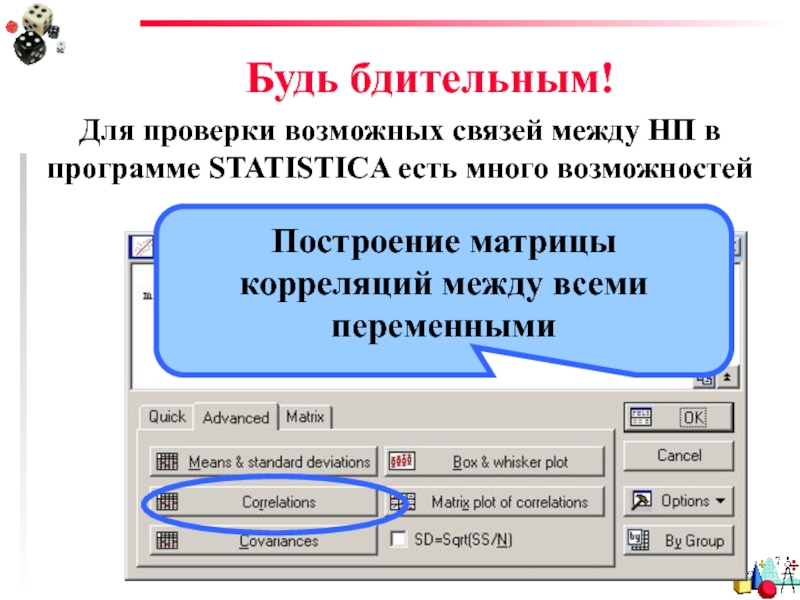
Слайд 86Будь бдительным!
Для проверки возможных связей между НП в программе STATISTICA есть
много возможностей
Построение матрицы корреляций между всеми переменными
Слайд 88Будь бдительным!
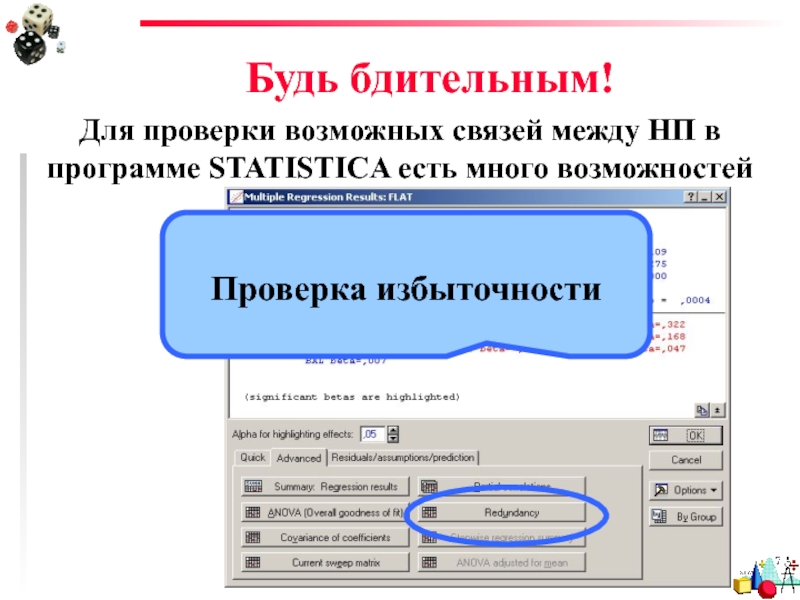
Для проверки возможных связей между НП в программе STATISTICA есть
много возможностей
Проверка избыточности
Слайд 89Будь бдительным!
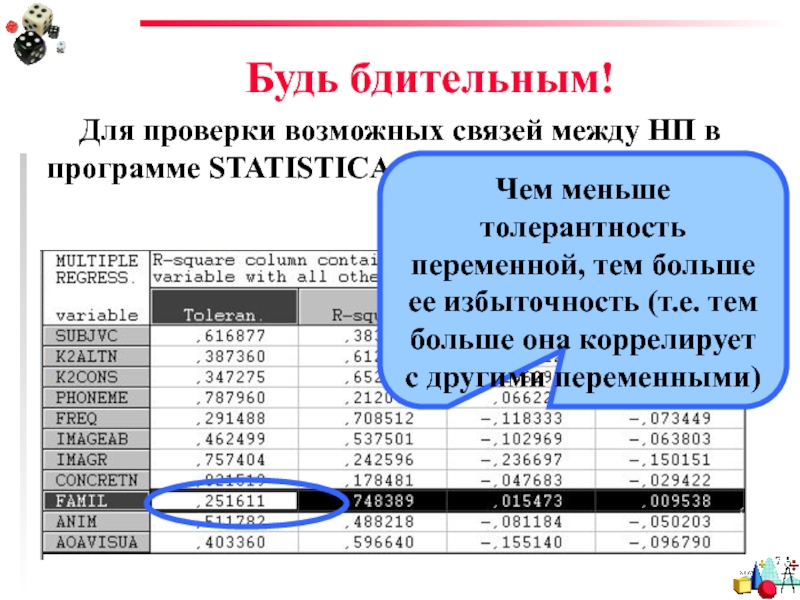
Для проверки возможных связей между НП в программе STATISTICA есть
много возможностей
Чем меньше толерантность переменной, тем больше ее избыточность (т.е. тем больше она коррелирует с другими переменными)
Слайд 90Будь бдительным!
Проверяйте наличие корреляций между независимыми переменными
и используйте пошаговые методы множественной
линейной регрессии
Слайд 91Шкалы наименований
В примере 3 использовались дихотомические шкалы.
А что делать, если попалась
шкала наименований?
Не спешите расстраиваться! Надо ее просто перекодировать!
Не спешите расстраиваться! Надо ее просто перекодировать!
Слайд 92Шкалы наименований
Если есть шкала «профессия» с кодами
1 – клерк
2 – охранник
3
– менеджер
то перекодируем ее в 3 переменных!
то перекодируем ее в 3 переменных!
Слайд 95К практическому занятию по регрессионному анализу надо прочитать:
Нестеренко А.И. и др.
Прогноз тревожности у студенток на основании их типологических различий// ПЖ, 2003, т.24, № 6, с. 37-46
Нечаева Е.С., Козубовский В.М. Ошибки интерпретации регрессионных моделей в психологических исследованиях// ПЖ (белорусский), 2006, т.26, № 2, с. 82-85
Нечаева Е.С., Козубовский В.М. Ошибки интерпретации регрессионных моделей в психологических исследованиях// ПЖ (белорусский), 2006, т.26, № 2, с. 82-85
Слайд 96А что делать, если зависимая переменная не количественная, а качественная?
Можно променять
ДИСКРИМИНАНТНЫЙ АНАЛИЗ!
