регрессии.
Линейная модель множественной регрессии.
Эмпирическая форма записи.
2. Оценка параметров модели с помощью МНК.
3. Показатели качества множественной регрессии.
4. Мультиколлинеарность.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейная модель множественной регрессии, оценка ее параметров. (Тема 3) презентация
Содержание
- 1. Линейная модель множественной регрессии, оценка ее параметров. (Тема 3)
- 2. Спецификация модели множественной регрессии Множественная регрессия представляет
- 3. Y X1 X2 a0 Чистый эффект
- 4. Y= a0+b1*x1+b2*x2+ e Y-общая величина расходов
- 6. Линейная модель множественной регрессии Факторы, включаемые во
- 7. 2 вопрос
- 8. Матричный метод вектор значений Y; -вектор
- 9. Матричный метод
- 10. Скалярный метод
- 11. МНК-оценки множественной регрессии
- 12. МНК-оценки множественной регрессии
- 13. Регрессионная модель в стандартизованном масштабе
- 14. Стандартизованные коэффициенты регрессии (β)
- 15. Благодаря тому, что в стандартизованном уравнении
- 16. Стандартизованные коэффициенты регрессии показывают, на сколько средних
- 17. В парной зависимости стандартизованный коэффициент регрессии есть
- 18. Частный коэффициент эластичности показывает, на сколько
- 19. Индекс множественной корреляции 3 вопрос Индекс множественной
- 20. Коэффициент детерминации: Скорректированный коэффициент детерминации: Коэффициент детерминации
- 21. Когда m - число параметров при Xj
- 23. Частные коэффициенты корреляции R2yx1x2…xj…xm – множественный коэффициент
- 24. Порядок частного коэффициента корреляции определяется количеством факторов,
- 25. F-критерий Фишера Значимость уравнения множественной регрессии в
- 26. t-статистика Стьюдента - оценка значимости коэффициентов регрессии
- 27. Задача: Предприниматель желает сдать в аренду на
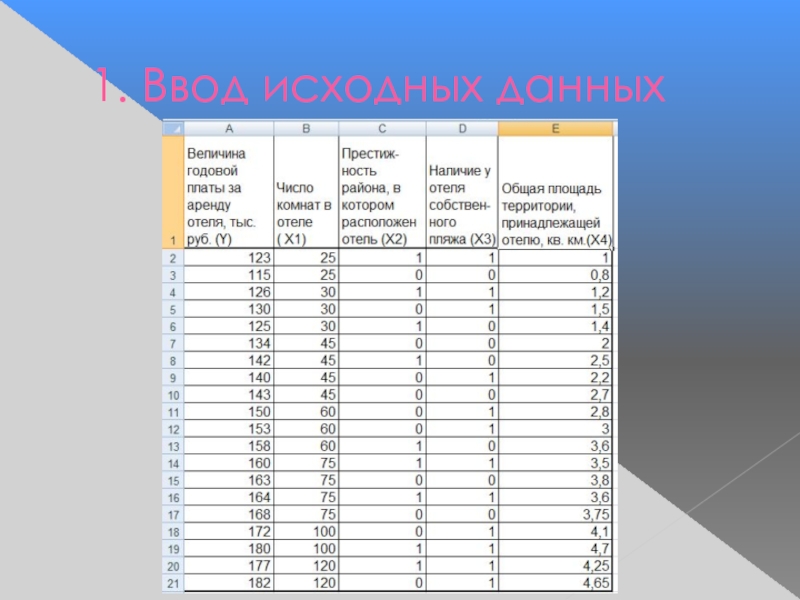
- 28. 1. Ввод исходных данных
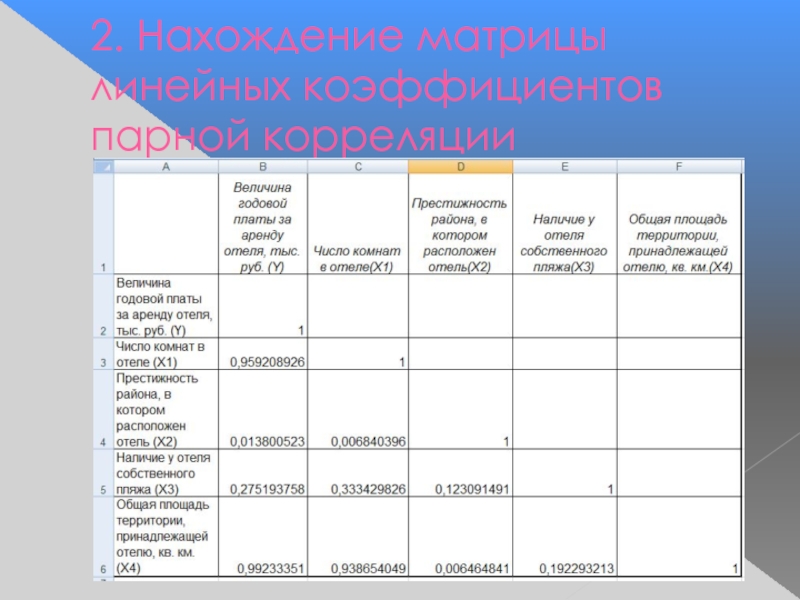
- 29. 2. Нахождение матрицы линейных коэффициентов парной корреляции
- 30. 3. Расчет оценок коэффициентов регрессии
- 31. Таким образом, построенная модель может быть
- 32. 4.Множественный коэффициент корреляции Множественный коэффициент корреляции
- 33. 5. Скорректированный коэффициент детерминации Скорректированный коэффициент детерминации
- 34. 6. Расчет бетта-коэффициентов Полученные значения бетта-коэффициентов позволяют
- 35. 7. F-тест Сравнение расчетного значения F-критерия с
- 36. 8. t-тест Сравнение модулей полученных t- статистик
- 37. 9. Расчет средней прогнозируемой величины арендной платы
- 38. ПОНЯТИЕ МУЛЬТИКОЛЛИНЕАРНОСТИ 4 вопрос Мультиколлинеарность - это
- 39. ДИАГРАММА ВЕННА Мультиколлинерность не позволяет однозначно разделить
- 40. ПОСЛЕДСТВИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ Увеличиваются стандартные ошибки оценок
- 41. ПРИЗНАКИ МУЛЬТИКОЛЛИНЕАРНОСТИ Высокий R2 Близкая к
- 42. Задача: Руководство коммерческого банка ищет пути уменьшения
- 43. 1. ВВОД ИСХОДНЫХ ДАННЫХ
- 44. 2. ПОСТРОЕНИЕ УРАВНЕНИЯ РЕГРЕССИИ
- 45. Полученный результат позволяет выдвинуть гипотезу о наличии коллинеарности факторов X1, X2!
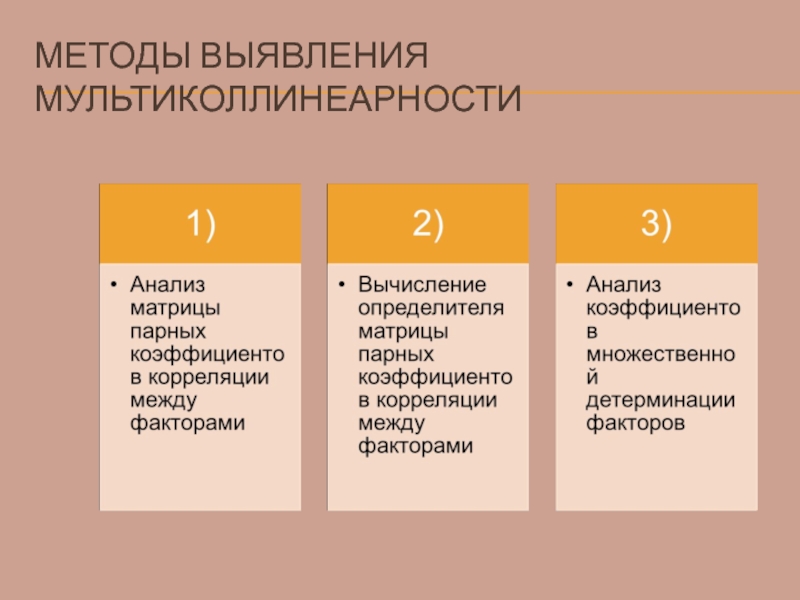
- 46. МЕТОДЫ ВЫЯВЛЕНИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ
- 47. Первый метод: Две переменные коллинеарны, т. е.
- 48. Предпочтение при этом отдается тому фактору, который
- 49. Второй метод: Если между факторами существует полная
- 50. 3.1. ПОСТРОЕНИЕ УРАВНЕНИЯ РЕГРЕССИИ С ФАКТОРОМ X1
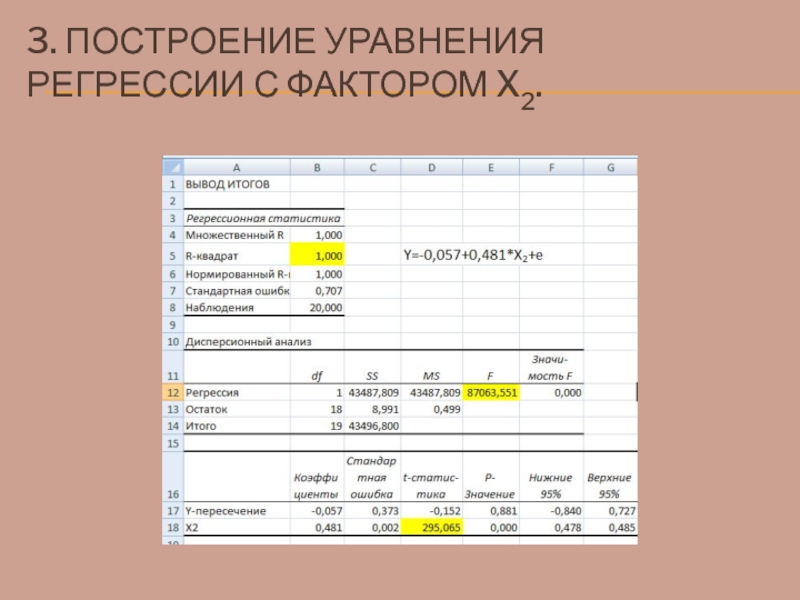
- 51. 3. ПОСТРОЕНИЕ УРАВНЕНИЯ РЕГРЕССИИ С ФАКТОРОМ X2.
- 52. Третий метод: Для расчета коэффициентов множественной
- 53. МЕТОДЫ УСТРАНЕНИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ Исключение из модели коррелированных
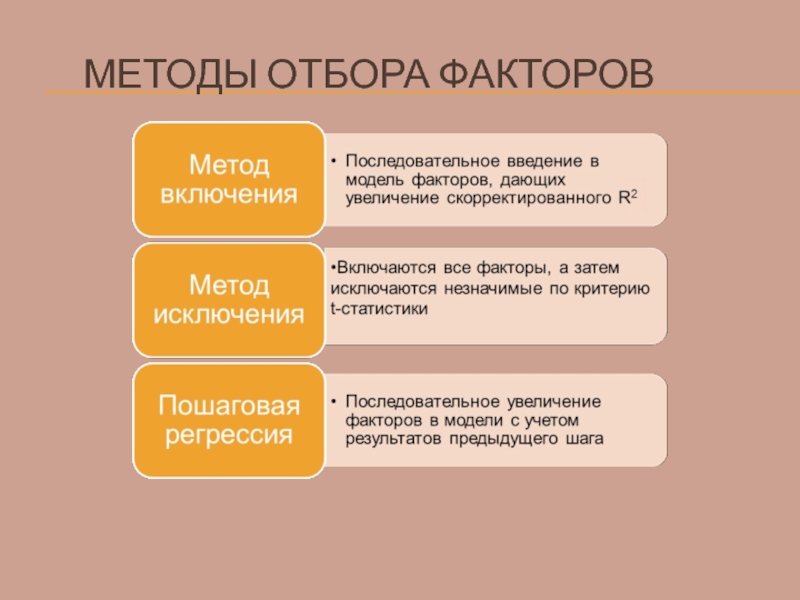
- 54. МЕТОДЫ ОТБОРА ФАКТОРОВ
- 55. ИСКЛЮЧЕНИЕ K ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ (исключение некорректно)
- 56. ВКЛЮЧЕНИЕ K ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ (включение оправдано)
Спецификация модели множественной регрессии Множественная регрессия представляет собой модель, где среднее значение зависимой переменной Y рассматри- вается как функция нескольких независимых переменных Xj. 1 вопрос
Слайд 1Тема 3. Линейная модель множественной регрессии, оценка ее параметров
Общая модель множественной
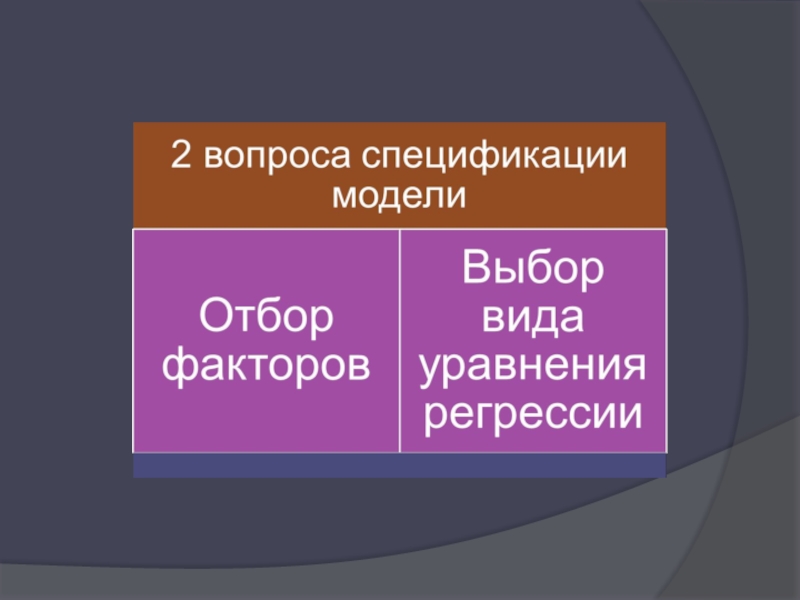
Слайд 2Спецификация модели множественной регрессии
Множественная регрессия представляет собой модель,
где среднее значение
зависимой переменной Y рассматри-
вается как функция нескольких независимых переменных Xj.
вается как функция нескольких независимых переменных Xj.
1 вопрос
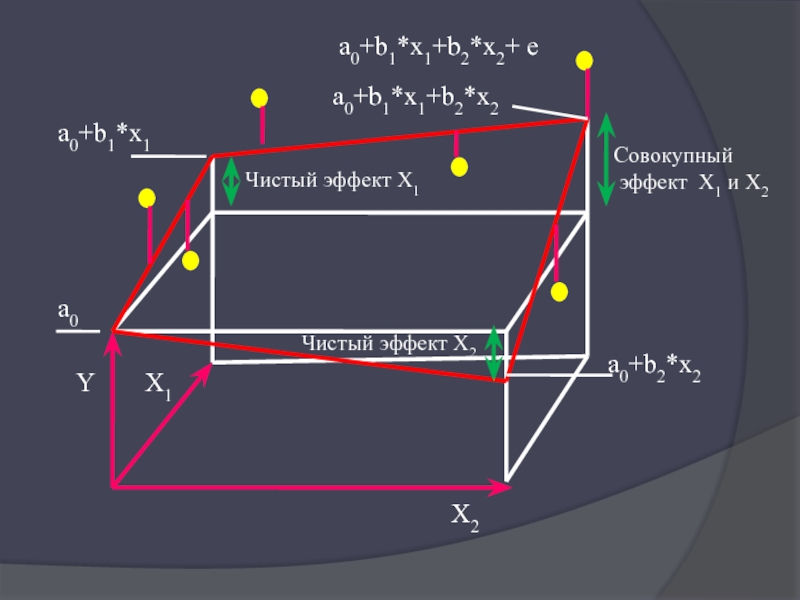
Слайд 3
Y
X1
X2
a0
Чистый эффект X2
Чистый эффект X1
Совокупный
эффект X1 и X2
a0+b2*x2
a0+b1*x1
a0+b1*x1+b2*x2
a0+b1*x1+b2*x2+ e
Слайд 4Y= a0+b1*x1+b2*x2+ e
Y-общая величина расходов на питание
X1- располагаемый личный доход,
X2- цена
продуктов питания
Экономическая интерпретация: При каждом увеличении
располагаемого личного доходаX1 на 1 единицу собственного
измерения, расходы на питание (Y) увеличиваются на b1
единиц измерения при сохранении постоянных цен.
На каждую единицу индекса цен X2 эти расходы уменьшаются
на b2 единиц измерения при сохранении постоянных доходов.
Если a0>0, то вариация расходов меньше вариации факторов;
если a0<0, то вариация расходов больше вариации факторов.
Слайд 6Линейная модель множественной регрессии
Факторы, включаемые во множественную регрессию:
должны быть количественно
измеримы;
не должны быть коррелированы между собой и тем более
находиться в точной функциональной связи.
не должны быть коррелированы между собой и тем более
находиться в точной функциональной связи.
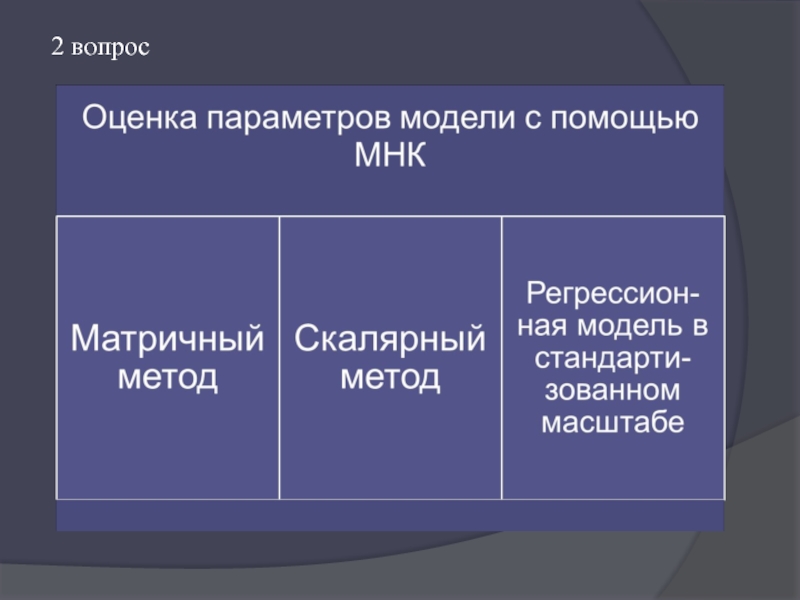
Слайд 8Матричный метод
вектор значений Y;
-вектор параметров
регрессии;
вектор остатков
регрессии .
матрица значений
X.
Слайд 15Благодаря тому, что в стандартизованном
уравнении все переменные заданы как
центрированные
и нормированные,
β-коэффициенты сравнимы между собой.
Сравнивая друг с другом β-коэффициенты,
можно ранжировать факторы по силе их
влияния на зависимую переменную Y.
Коэффициенты «чистой» регрессии (bj)
несравнимы между собой.
β-коэффициенты сравнимы между собой.
Сравнивая друг с другом β-коэффициенты,
можно ранжировать факторы по силе их
влияния на зависимую переменную Y.
Коэффициенты «чистой» регрессии (bj)
несравнимы между собой.
Слайд 16Стандартизованные коэффициенты регрессии показывают, на сколько средних квадратических отклонений (σy) изменится
в среднем результат, если соответствующий фактор xj изменится на одну сигму (σxi) при неизменном среднем уровне других факторов
Слайд 17В парной зависимости стандартизованный коэффициент регрессии есть линейный коэффициент корреляции:
Во множественной
регрессии зависимость следующая:
Слайд 18Частный коэффициент эластичности
показывает, на сколько % изменяется в среднем
результативный
признак Y при изменении фактора Xj на
1% и при неизменных других факторах, включенных в модель
1% и при неизменных других факторах, включенных в модель
Слайд 19Индекс множественной корреляции
3 вопрос
Индекс множественной корреляции независимо от формы
связи оценивает тесноту
совместного влияния факторов
на результативный признак Y:
на результативный признак Y:
При линейной регрессии:
Слайд 20Коэффициент детерминации:
Скорректированный коэффициент детерминации:
Коэффициент детерминации
Слайд 21Когда m - число параметров при Xj –
приближается к объему
наблюдений (n), то
остаточная дисперсия будет близка к нулю и
R2 приблизится к 1 даже при слабой связи
факторов с результатом. Скорректированный
R2 содержит поправку на число степеней
свободы, что не допускает возможного
преувеличения тесноты связи.
остаточная дисперсия будет близка к нулю и
R2 приблизится к 1 даже при слабой связи
факторов с результатом. Скорректированный
R2 содержит поправку на число степеней
свободы, что не допускает возможного
преувеличения тесноты связи.
Слайд 23Частные коэффициенты корреляции
R2yx1x2…xj…xm – множественный коэффициент детерминации
всего комплекса факторов с результатом;
R2yx1x2…xj-1xj+1…xm
– тот же показатель детерминации, но без введения в модель фактора xj
Слайд 24Порядок частного коэффициента корреляции определяется
количеством факторов, влияние которых исключается.
Коэффициенты частной корреляции
первого порядка:
Коэффициенты парной корреляции называются
коэффициентами нулевого порядка
Слайд 25F-критерий Фишера
Значимость уравнения множественной регрессии в целом,
так же как и
в парной регрессии, оценивается с помощью
F-критерия Фишера:
F-критерия Фишера:
2 вопрос
Слайд 27Задача: Предприниматель желает сдать в аренду на один год принадлежащий ему
отель (80 комнат), расположенный в престижной курортной зоне, обладающий собственным пляжем, общая площадь территории отеля составляет 3,42 кв. км. Для установления величины арендной платы, предприниматель решил изучить объявления владельцев подобных отелей и смоделировать величину арендной платы.
Слайд 31Таким образом, построенная модель может быть
записана в виде Y=101,84+3,58*X3+16,21*X4+e .
Коэффициент
b3 этой модели показывает, что наличие у отеля собственного пляжа приводит к удорожанию арендной платы в среднем на 3,58 тыс. руб. при неизменной общей территории, принадлежащей отелю.
Коэффициент b4 этой модели показывает, что увеличение
общей территории на 1 кв.км приводит к удорожанию
арендной платы на 16,21 тыс.руб.
Коэффициент b4 этой модели показывает, что увеличение
общей территории на 1 кв.км приводит к удорожанию
арендной платы на 16,21 тыс.руб.
Слайд 324.Множественный коэффициент корреляции
Множественный коэффициент корреляции достаточно высокий, что свидетельствует о
существенной зависимости величины арендной платы от включенных в модель факторов.
Слайд 335. Скорректированный коэффициент детерминации
Скорректированный коэффициент детерминации
свидетельствует, что 99,12% дисперсии арендной
платы
формируется под влиянием факторов, включенных в модель.
формируется под влиянием факторов, включенных в модель.
Слайд 346. Расчет бетта-коэффициентов
Полученные значения бетта-коэффициентов позволяют проранжировать факторы по степени их
влияния на арендную плату следующим образом:
общая площадь территории, принадлежащей отелю;
наличие собственного пляжа.
общая площадь территории, принадлежащей отелю;
наличие собственного пляжа.
Слайд 357. F-тест
Сравнение расчетного значения F-критерия с табличным
(1069,9398 > 3,5915) с
вероятностью 95% позволяет сделать
вывод об адекватности и статистической значимости модели
в целом.
вывод об адекватности и статистической значимости модели
в целом.
Слайд 368. t-тест
Сравнение модулей полученных t- статистик с табличным значением (2,1098) подтверждает
значимость коэффициентов регрессии b0,b3,b4.
Слайд 379. Расчет средней прогнозируемой величины арендной платы
Y=101,84+3,58*X3+16,21*X4+e; X3=1; X4=3,42 кв.км
Yx=101,84+3,58*1+16,21*3,42=160,8846≈161
тыс.руб.
Слайд 38ПОНЯТИЕ МУЛЬТИКОЛЛИНЕАРНОСТИ
4 вопрос
Мультиколлинеарность - это линейная взаимосвязь нескольких объясняющих переменных (х1,
х2, … хm). Если объясняющие переменные связаны строгой функциональной зависимостью, то говорят о совершенной мультиколлинеарности.
Слайд 39ДИАГРАММА ВЕННА
Мультиколлинерность не позволяет однозначно разделить
вклады объясняющих переменных x1,x2,…xm в
их влияние
на зависимую переменную Y.
на зависимую переменную Y.
X2
X1
X2
Y
Y
X1
X1=X2
Y
х1 и х2 коллинеарны
х1 и х2 не коллинеарны
совершенная коллинеарность х1 и х2
Слайд 40ПОСЛЕДСТВИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ
Увеличиваются стандартные ошибки оценок
Уменьшаются t-статистики МНК-оценок регрессии
МНК-оценки чувствительны к изменениям
данных
Возможность неверного знака МНК-оценок
Трудность в определении вклада независимых переменных в дисперсию зависимой переменной
Возможность неверного знака МНК-оценок
Трудность в определении вклада независимых переменных в дисперсию зависимой переменной
Слайд 41ПРИЗНАКИ МУЛЬТИКОЛЛИНЕАРНОСТИ
Высокий R2
Близкая к 1 парная корреляция между малозначимыми независимыми переменными
Высокие
частные коэффициенты корреляции
Сильная дополнительная регрессия между независимыми переменными
Сильная дополнительная регрессия между независимыми переменными
2 вопрос
Слайд 42Задача: Руководство коммерческого банка ищет пути уменьшения расходов, связанных с основным
видом деятельности – размещением вкладов физических лиц. С этой целью по данным за последние 20 кварталов было решено проанализировать , в какой мере среднеквартальное число клиентов (Y) определяется величиной затрат на рекламу (X1) и суммой расходов на связи с общественностью (X2).
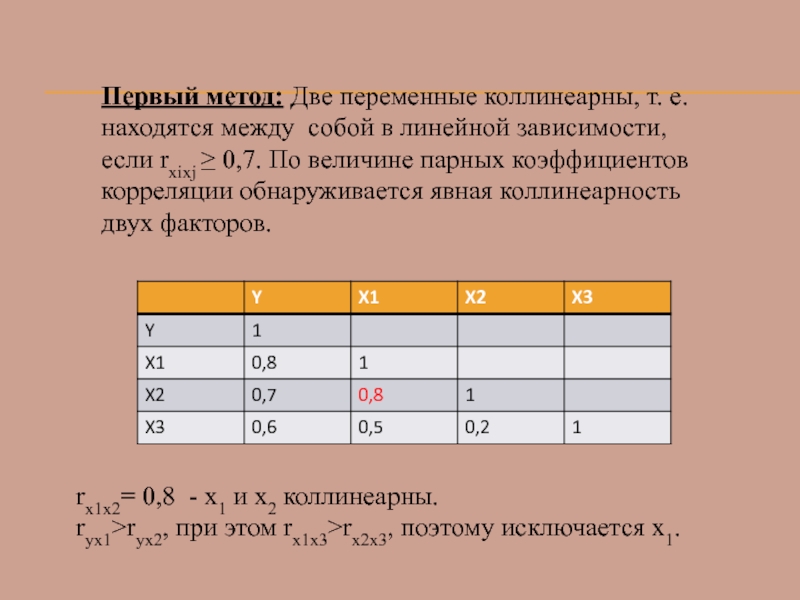
Слайд 47Первый метод: Две переменные коллинеарны, т. е. находятся между собой в
линейной зависимости, если rxixj ≥ 0,7. По величине парных коэффициентов корреляции обнаруживается явная коллинеарность двух факторов.
rx1x2= 0,8 - x1 и x2 коллинеарны.
ryx1>ryx2, при этом rx1x3>rx2x3, поэтому исключается x1.
Слайд 48Предпочтение при этом отдается тому фактору, который при достаточно тесной связи
с результатом имеет наименьшую тесноту связи с другими факторами!
Слайд 49Второй метод: Если между факторами существует полная
линейная зависимость, и все
коэффициенты межфакторной
корреляции равны единице, то определитель такой матрицы
равен нулю. Следовательно, чем ближе к нулю определитель,
тем сильнее мультиколлинеарность факторов.
корреляции равны единице, то определитель такой матрицы
равен нулю. Следовательно, чем ближе к нулю определитель,
тем сильнее мультиколлинеарность факторов.
Δ=1*1-1*1=0. Равенство определителя нулю говорит о наличии
мультиколлинеарности в строгом смысле. Следовательно, необходимо
исключить один из факторов и перестроить модель заново.
Слайд 52Третий метод: Для расчета коэффициентов множественной
детерминации факторов в качестве зависимой
переменной
рассматривается каждый из факторов. Например,
рассматривается каждый из факторов. Например,
Чем ближе такой коэффициент множественной детерминации
к единице, тем сильнее проявляется мультиколлинеарность
факторов. В уравнении регрессии оставляют факторы с
минимальным коэффициентом множественной детерминации.
Если коэффициент детерминации статистически значим, то в
этом случае xj является линейной комбинацией других факторов, и его можно исключить из регрессии.
Слайд 53МЕТОДЫ УСТРАНЕНИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ
Исключение из модели коррелированных переменных ( при отборе факторов)
Сбор
дополнительных данных или новая выборка
Изменение спецификации модели
Использование предварительной информации о параметрах
Преобразование переменных
Изменение спецификации модели
Использование предварительной информации о параметрах
Преобразование переменных
