- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Справочник по геометрии 7-9 класс презентация
Содержание
- 1. Справочник по геометрии 7-9 класс
- 2. Не секрет, что порою для
- 3. Цели и задачи создания справочника: систематизировать материал
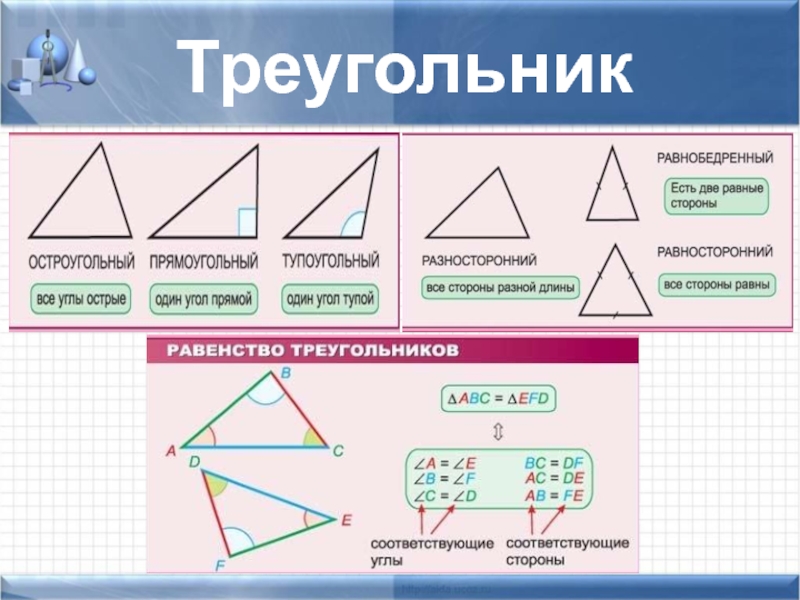
- 4. Треугольник
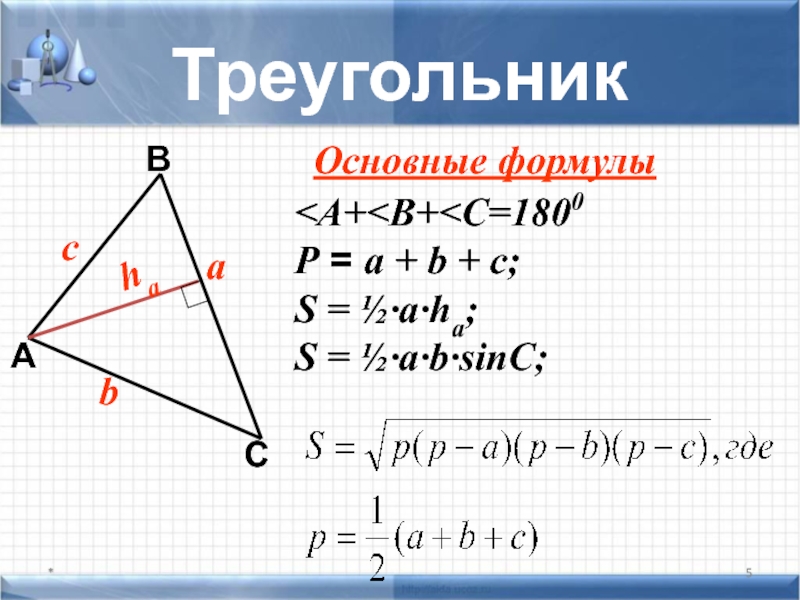
- 5. Треугольник * А С В b с а
- 6. Свойства равнобедренного треугольника В равнобедренном треугольнике углы
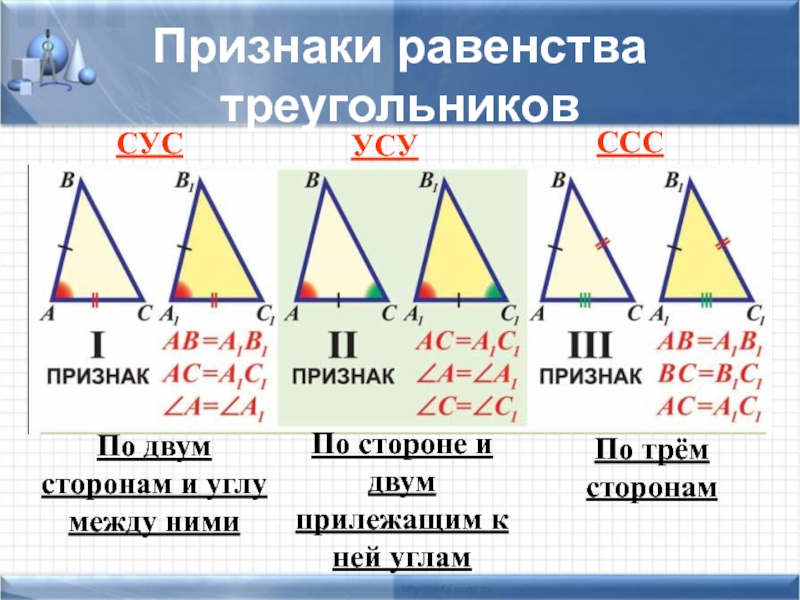
- 7. Признаки равенства треугольников СУС УСУ ССС По
- 8. Признаки равенства прямоугольных треугольников
- 9. Свойства прямоугольного треугольника В прямоугольном треугольнике сумма
- 10. С В А Соотношения между сторонами
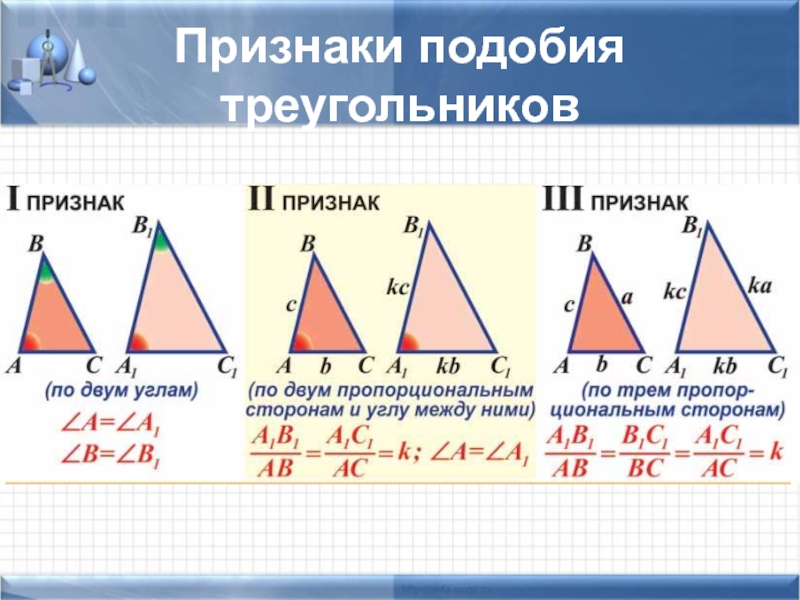
- 11. Признаки подобия треугольников
- 12. h
- 13. с2 =а2+b2 Теорема: В прямоугольном треугольнике квадрат
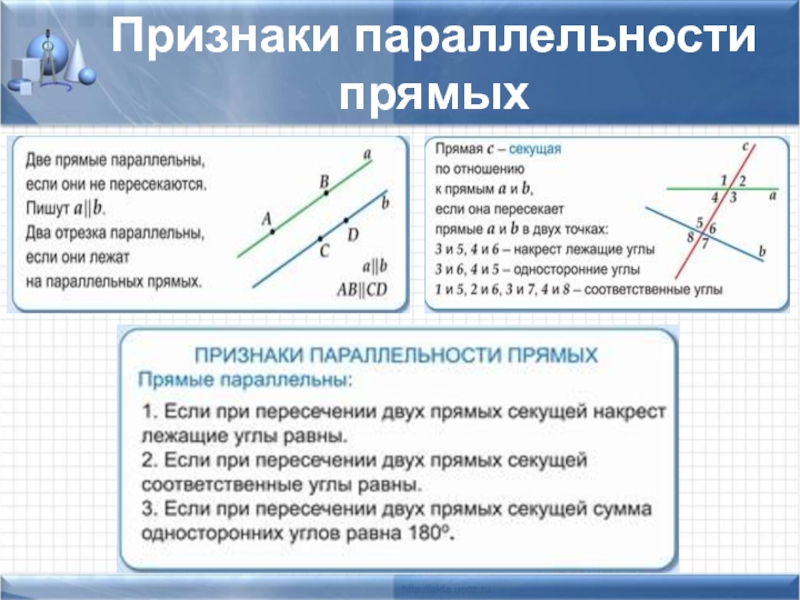
- 14. Признаки параллельности прямых
- 15. Параллелограммом называется четырехугольник, у которого противоположные стороны
- 16. D А В С Параллелограмм О
- 17. Квадрат - это прямоугольник, у которого все
- 18. Прямоугольником называется параллелограмм, у которого все углы
- 19. Прямоугольник А O D С В Основные формулы a b
- 20. Все стороны ромба равны
- 21. А В С D О Ромб
- 22. Четырехугольник, у которого две стороны параллельны, а
- 23. Соотношения между сторонами и углами в прямоугольном
- 24. Окружность О А ОА -
- 25. Окружность Основные формулы d = 2r C
- 26. Федеральный компонент государственного образовательного стандарта основного общего
Слайд 2 Не секрет, что порою для решения задачи не хватает
Важную роль играет использование математического справочника при самоподготовке к ЕГЭ в 11 классе и ГИА в 9 классе.
Создание справочника не закончено. Собраны основные формулы по курсу геометрии 7-9 классов. Работа над созданием справочника продолжается
Номинация: интерактивная презентация к урокам
Слайд 3Цели и задачи создания справочника:
систематизировать материал по основным математическим понятиям и
создать учащимся условия для беспроблемного решения многих математических задач при выполнении домашнего задания, при подготовке к контрольным и самостоятельным работам, к ЕГЭ и ГИА;
способствовать развитию познавательной активности учащихся через знакомство с формулами, облегчающими процесс решения задачи;
способствовать развитию математических способностей одарённых детей через знакомство с формулами, не входящими в школьную программу по математике.
Слайд 6Свойства равнобедренного треугольника
В равнобедренном треугольнике углы при основании равны
Медиана, проведенная к
ВD-биссектриса
ВD-высота
А
В
С
<А = <С
D
1
2
Слайд 7Признаки равенства треугольников
СУС
УСУ
ССС
По двум сторонам и углу между ними
По стороне и
По трём сторонам
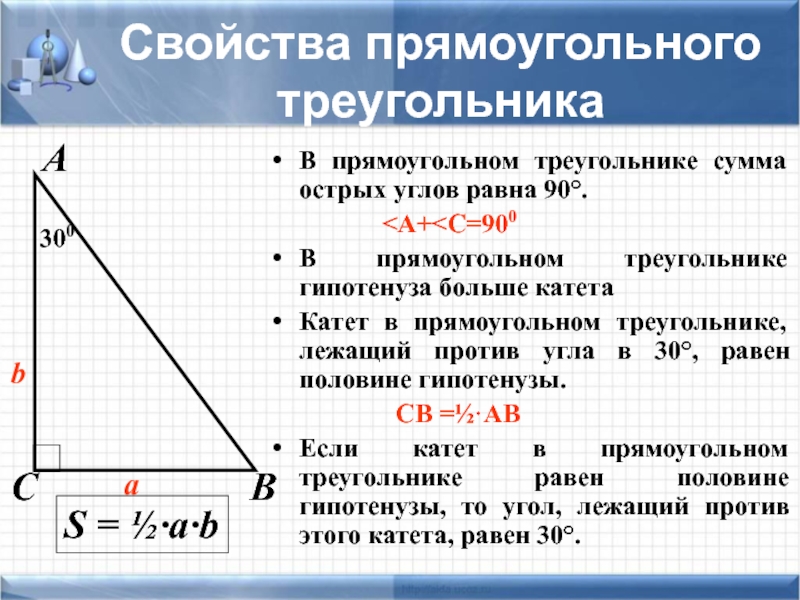
Слайд 9Свойства прямоугольного треугольника
В прямоугольном треугольнике сумма острых углов равна 90°.
Катет в прямоугольном треугольнике, лежащий против угла в 30°, равен половине гипотенузы.
CB =½·AB
Если катет в прямоугольном треугольнике равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
A
B
C
300
a
b
S = ½·a·b
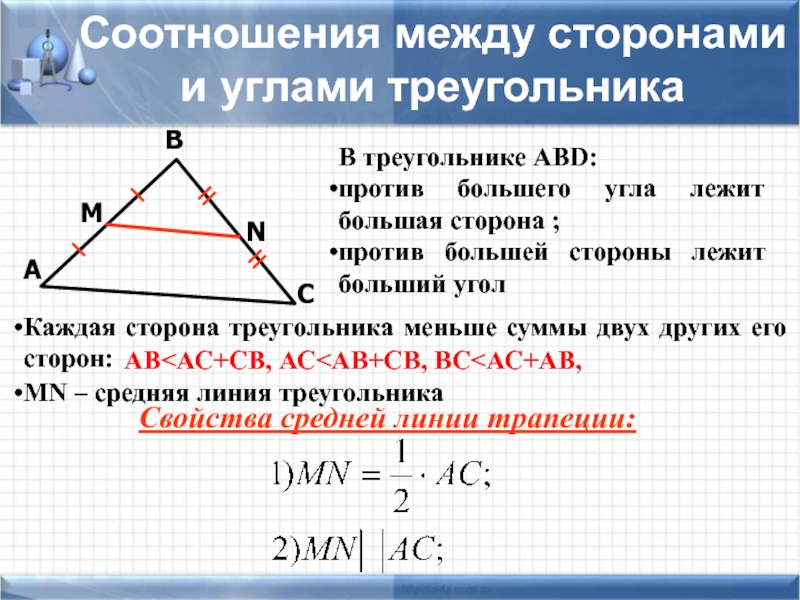
Слайд 10С
В
А
Соотношения между сторонами и углами треугольника
В треугольнике АВD:
против большего угла лежит
против большей стороны лежит больший угол
АВ<АС+СВ, АС<АВ+СВ, ВС<АС+АВ,
Каждая сторона треугольника меньше суммы двух других его сторон:
M
N
MN – средняя линия треугольника
Свойства средней линии трапеции:
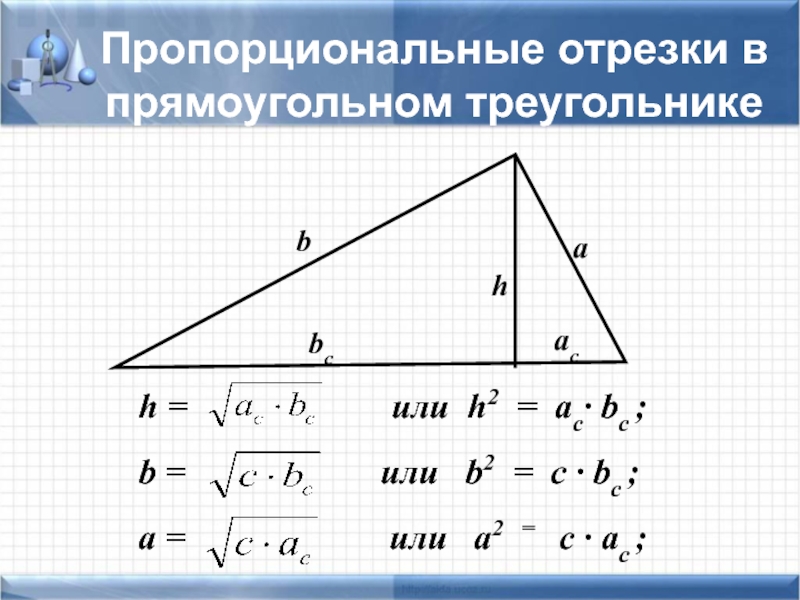
Слайд 12 h =
b = или b2 = c · bc ;
a = или a2 = c · ac ;
b
a
h
bc
ac
Пропорциональные отрезки в прямоугольном треугольнике
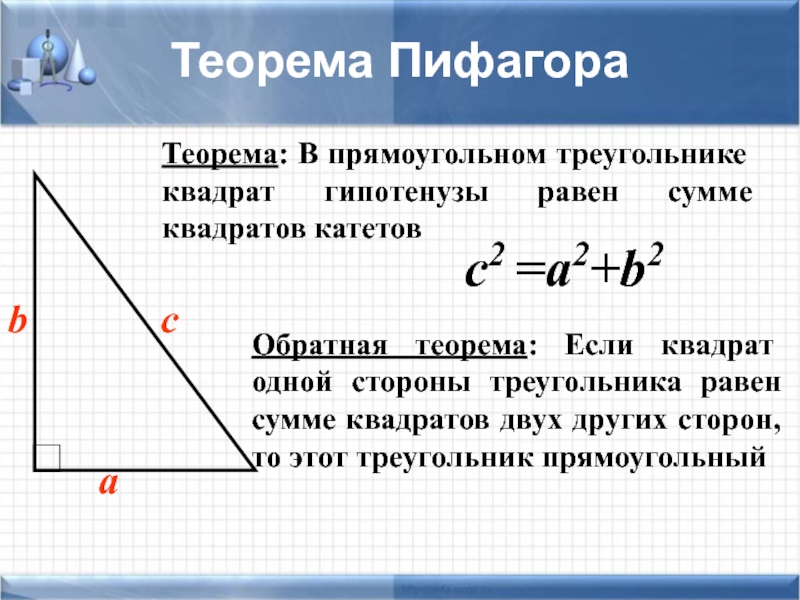
Слайд 13с2 =а2+b2
Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Теорема
Обратная теорема: Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то этот треугольник прямоугольный
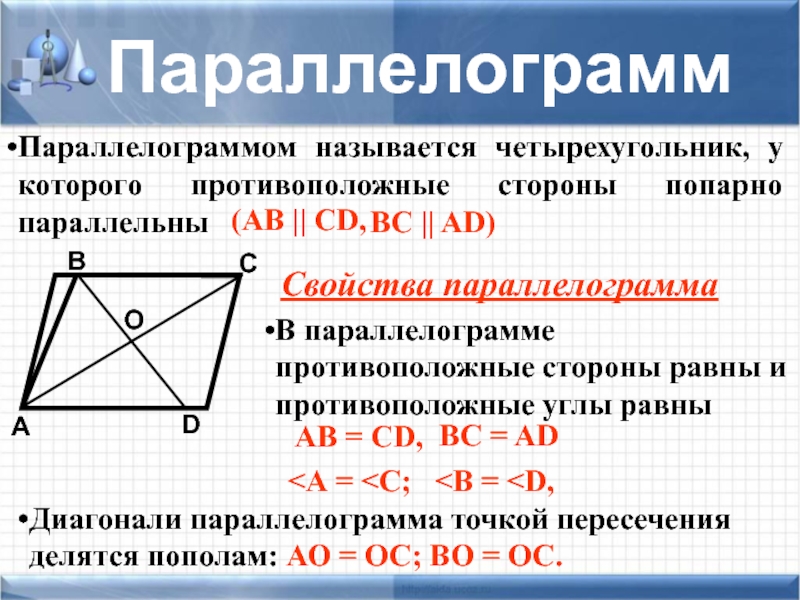
Слайд 15Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны
D
А
В
С
(АB || CD,
BC
Параллелограмм
В параллелограмме противоположные стороны равны и противоположные углы равны
Диагонали параллелограмма точкой пересечения делятся пополам: АО = ОС; ВО = ОС.
АB = CD,
BC = AD
<А = <С;
О
Свойства параллелограмма
Слайд 16
D
А
В
С
Параллелограмм
О
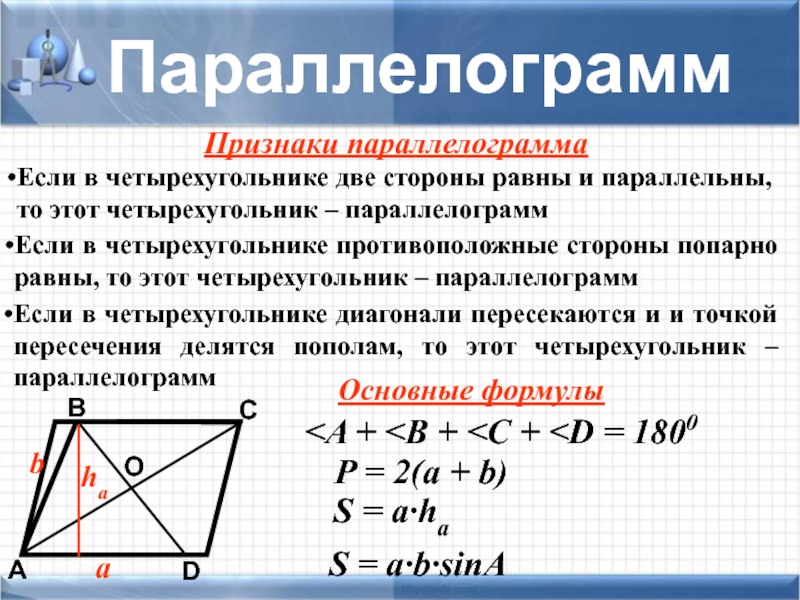
S = a·ha
ha
S = a·b·sinA
Признаки параллелограмма
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм
Если в четырехугольнике диагонали пересекаются и и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм
Основные формулы
Слайд 17Квадрат - это прямоугольник, у которого все стороны равны.
а
а
Квадрат
Квадрат обладает всеми
Основные формулы
А D С В P = 4a S = a2 S = ½·P·r (R-радиус описанной окружности)
(r-радиус вписанной окружности)
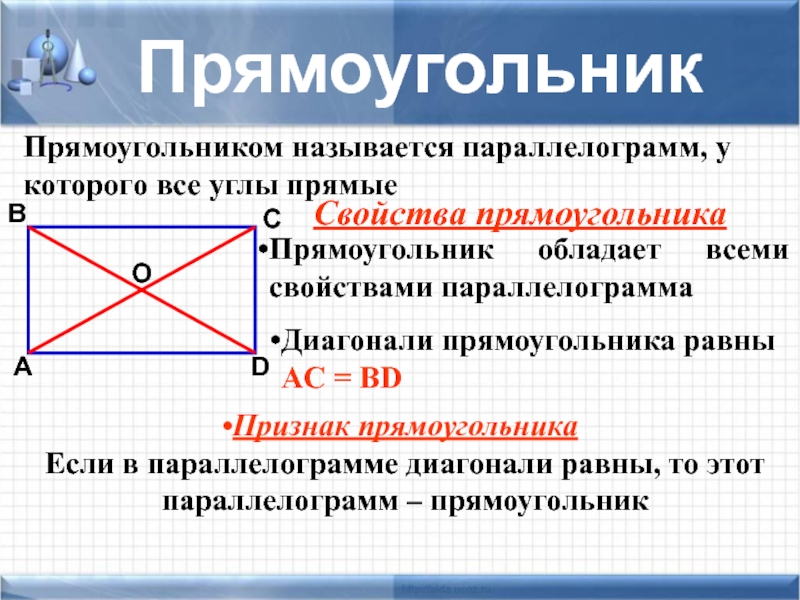
Слайд 18Прямоугольником называется параллелограмм, у которого все углы прямые
Прямоугольник
А
O
D
С
В
Диагонали прямоугольника равны
Признак прямоугольника
Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник
Свойства прямоугольника
Прямоугольник обладает всеми свойствами параллелограмма
Слайд 19Прямоугольник
А
O
D
С
В
Основные формулы
a
b
S = a·b
Прямоугольником называется параллелограмм, у которого все углы прямые
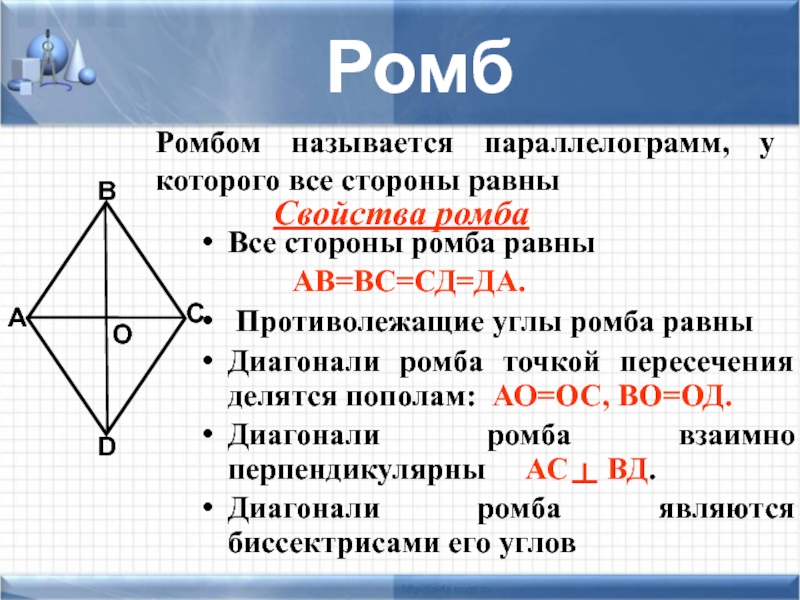
Слайд 20Все стороны ромба равны
АВ=ВС=СД=ДА.
Противолежащие углы ромба
Диагонали ромба точкой пересечения делятся пополам: АО=ОС, ВО=ОД.
Диагонали ромба взаимно перпендикулярны АС ВД.
Диагонали ромба являются биссектрисами его углов
А
В
С
D
О
Ромб
Ромбом называется параллелограмм, у которого все стороны равны
Свойства ромба
Слайд 21
А
В
С
D
О
Ромб
Ромбом называется параллелограмм, у которого все стороны равны
Основные формулы
AВ = BС
P = 4a
a
d1
d2
S = ½·d1·d2
Слайд 22Четырехугольник, у которого две стороны параллельны, а две другие нет, называется
A
B
C
D
BC, AD–основания трапеции, ВС║АD
AB,CD – боковые стороны
Трапеция
M
N
MN –средняя линия трапеции
Свойства
средней линии трапеции:
P = АВ+ВС+СD+AD
Основные формулы
a
b
h
В равнобедренной трапеции углы при основаниях равны
В равнобедренной трапеции диагонали равны
Слайд 23Соотношения между сторонами и углами в прямоугольном треугольнике
а
b
с
А
В
С
Противолежащий катет
Прилежащий катет
Гипотенуза
-основное
тождество
Таблица значений sinα, cosα, tgα для некоторых углов
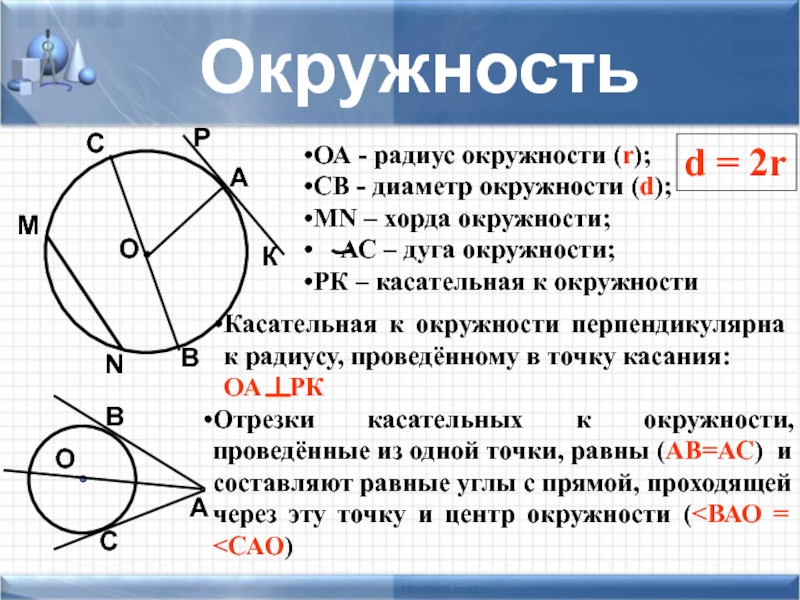
Слайд 24Окружность
О
А
ОА - радиус окружности (r);
СВ - диаметр окружности (d);
MN – хорда
АС – дуга окружности;
РК – касательная к окружности
С
В
М
N
Р
К
Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания:
ОА РК
Отрезки касательных к окружности, проведённые из одной точки, равны (АВ=АС) и составляют равные углы с прямой, проходящей через эту точку и центр окружности (<ВАО = <САО)
d = 2r
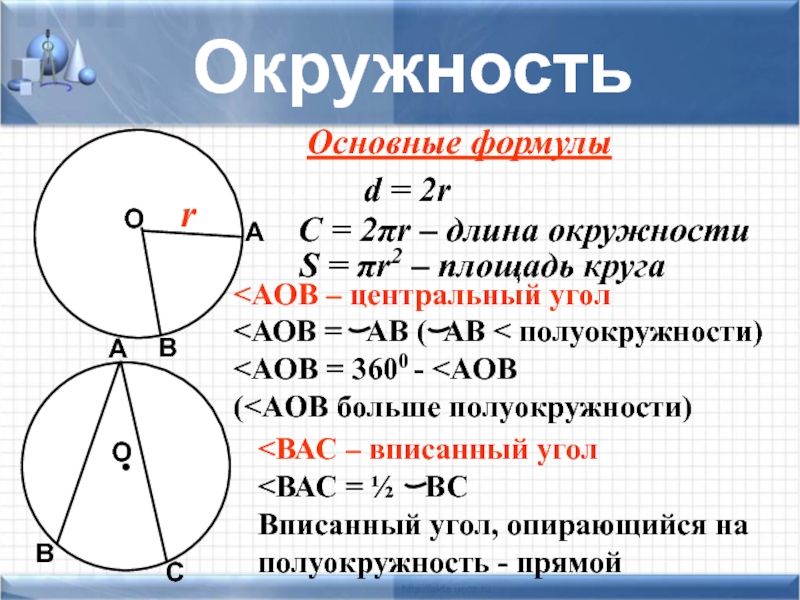
Слайд 25Окружность
Основные формулы
d = 2r
C = 2πr – длина окружности
S = πr2
r
А
В
О
А В О С <ВАС – вписанный угол
<ВАС = ½ ВС
Вписанный угол, опирающийся на
полуокружность - прямой
Слайд 26Федеральный компонент государственного образовательного стандарта основного общего образования по математике (пр.министерства
Авторская программа Атанасян Л.С., Бутузов В.Ф., Кодомцев С.Б. составитель БурмистроваТ.А., М. «Просвещение», 2009
УМК «Геометрия 7-9» Атанасян Л.С., Бутузов В.Ф.,и др- М.:Просвещение, 2009г
Интернет – ресурсы:
http://www.gcro.ru/index.php?option=com_content&view=article&id=208:matrp&catid=91:mathmat&Itemid=6922
http://www.it-n.ru/communities.aspx?cat_no=4510&lib_no=117550&tmpl=lib
Литература: