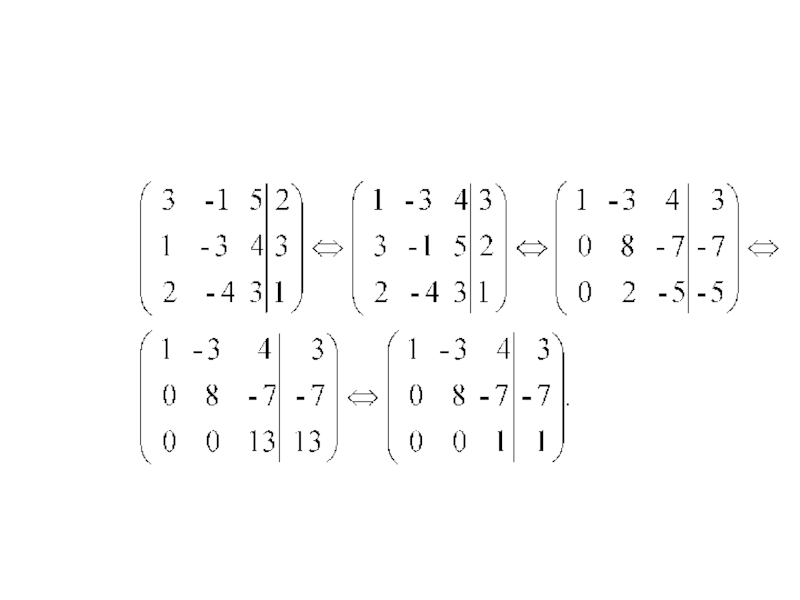- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейная алгебра. Ранг матрицы. (Тема 2) презентация
Содержание
- 1. Линейная алгебра. Ранг матрицы. (Тема 2)
- 3. С помощью элементарных преобразований можно привести
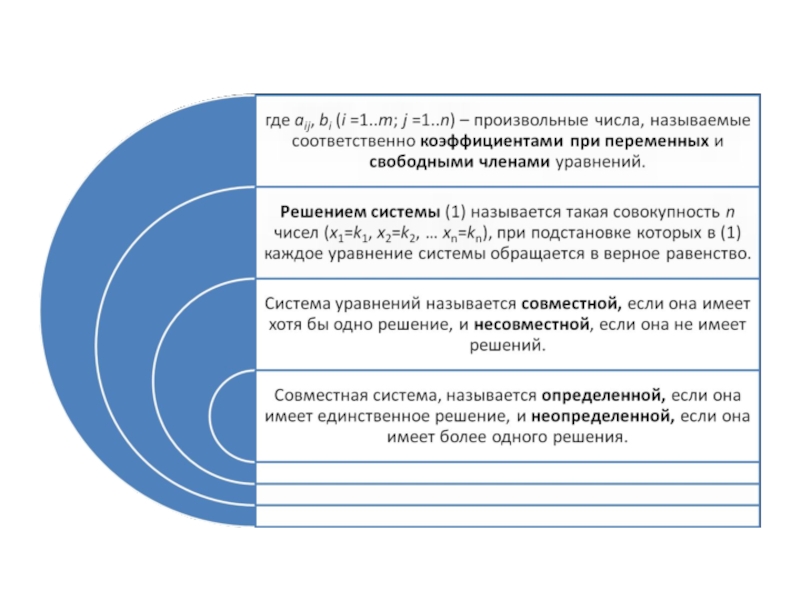
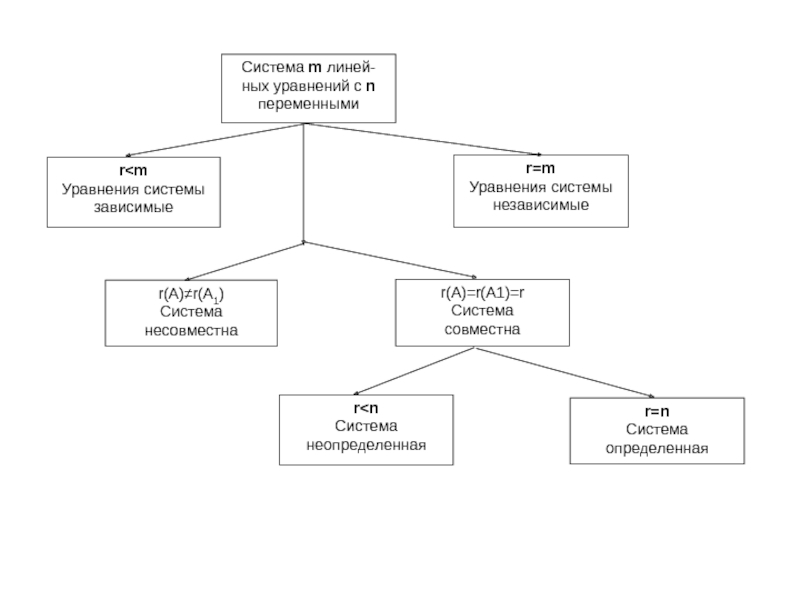
- 4. Система линейных уравнений Система m линейных уравнений с n переменными имеет вид:
- 6. Запишем систему (1) в матричной
- 7. Системы n линейных уравнений с n переменными
- 8. Метод Крамера Теорема Крамера. Пусть Δ –
- 9. Метод Гаусса Метод Гаусса – метод
- 10. П р и м е р 1.
- 12. Обратный ход метода Гаусса.
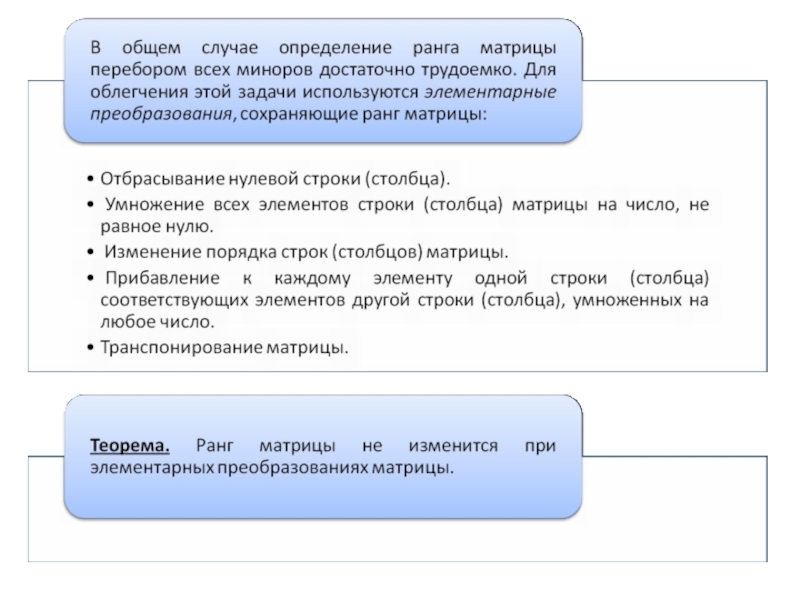
Слайд 3С помощью элементарных преобразований
можно привести матрицу к ступенчатому виду:
Ранг ступенчатой
матрицы равен r ,
так как имеется минор r-го порядка неравный нулю
│А│= а11∙а22 ∙…∙аrr.
так как имеется минор r-го порядка неравный нулю
│А│= а11∙а22 ∙…∙аrr.
Слайд 6
Запишем систему (1) в матричной форме.
Обозначим: А – матрица коэффициентов
при переменных, или матрица системы, Х – матрица-столбец переменных; В – матрица-столбец свободных членов.
Систему (1) можно записать в виде:
АХ=В.
Систему (1) можно записать в виде:
АХ=В.
Слайд 7Системы n линейных уравнений с n переменными
Пусть число уравнений системы (1)
равно числу переменных, т.е. m=n. Тогда матрица системы является квадратной, а её определитель Δ=│А│называется определителем системы.
Предположим, что │А│не равен нулю, тогда существует обратная матрица А-1.
Умножая слева обе части матричного равенства на обратную матрицу А-1 получим:
А-1 (АХ)= А-1 В.
(А-1 А)Х =ЕХ =Х
Решением системы уравнений методом обратной матрицы будет матрица-столбец:
Х= А-1В.
Предположим, что │А│не равен нулю, тогда существует обратная матрица А-1.
Умножая слева обе части матричного равенства на обратную матрицу А-1 получим:
А-1 (АХ)= А-1 В.
(А-1 А)Х =ЕХ =Х
Решением системы уравнений методом обратной матрицы будет матрица-столбец:
Х= А-1В.
Слайд 8Метод Крамера
Теорема Крамера. Пусть Δ – определитель матрицы системы А, а
Δj – определитель матрицы, полученный из матрицы заменой j-го столбца столбцом свободных членов. Тогда если Δ не равен нулю, то система имеет единственное решение, определённое по формулам Крамера:
Слайд 9Метод Гаусса
Метод Гаусса – метод последовательного исключения переменных – заключается
в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого или треугольного вида.
Рассмотрим матрицу:
эта матрица называется расширенной матрицей системы (1), так как в нее кроме матрицы системы А, дополнительно включен столбец свободных членов.
Рассмотрим матрицу:
эта матрица называется расширенной матрицей системы (1), так как в нее кроме матрицы системы А, дополнительно включен столбец свободных членов.
Слайд 10П р и м е р 1. Методом Гаусса решить систему:
Р
е ш е н и е.
Прямой ход метода Гаусса.
Запишем расширенную матрицу системы
и с помощью элементарных преобразований приведём матрицу к треугольному виду:
1. Поменяем местами 1-ю и 2-ю строки.
2. 1-ю строку умножим на (-3) и прибавим ко 2-й,
потом 1-ю умножим на (-2) и прибавим к 3-й.
3. 3-ю строку умножим на (-4) и прибавим ко 2-й, получим эквивалентную матрицу.
4. 3-ю строку разделим на 13
Прямой ход метода Гаусса.
Запишем расширенную матрицу системы
и с помощью элементарных преобразований приведём матрицу к треугольному виду:
1. Поменяем местами 1-ю и 2-ю строки.
2. 1-ю строку умножим на (-3) и прибавим ко 2-й,
потом 1-ю умножим на (-2) и прибавим к 3-й.
3. 3-ю строку умножим на (-4) и прибавим ко 2-й, получим эквивалентную матрицу.
4. 3-ю строку разделим на 13