- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 08. Однородные координаты презентация
Содержание
- 1. Лекция 08. Однородные координаты
- 2. 1. Вводные замечания
- 3. В аналитической геометрии под «координатами» геометрического объекта
- 4. Примеры 1) Точка определяется своими
- 5. Примеры 1) Точка определяется своими
- 6. Примеры 1) Точка определяется своими
- 7. Примеры 1) Точка определяется своими
- 8. Примеры 1) Точка определяется своими
- 9. То есть, отталкиваемся от множества чисел x,
- 10. То есть, отталкиваемся от множества чисел x,
- 11. То есть, отталкиваемся от множества чисел x,
- 12. То есть, отталкиваемся от множества чисел x,
- 13. 2. Однородные координаты
- 14. Обыкновенная аналитическая геометрия: прямоугольные
- 15. Обыкновенная аналитическая геометрия: прямоугольные
- 16. Обыкновенная аналитическая геометрия: прямоугольные
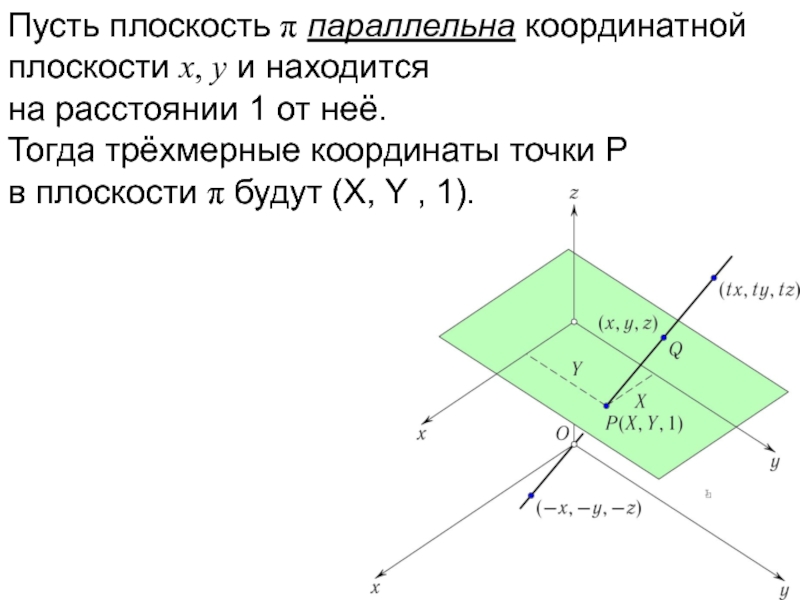
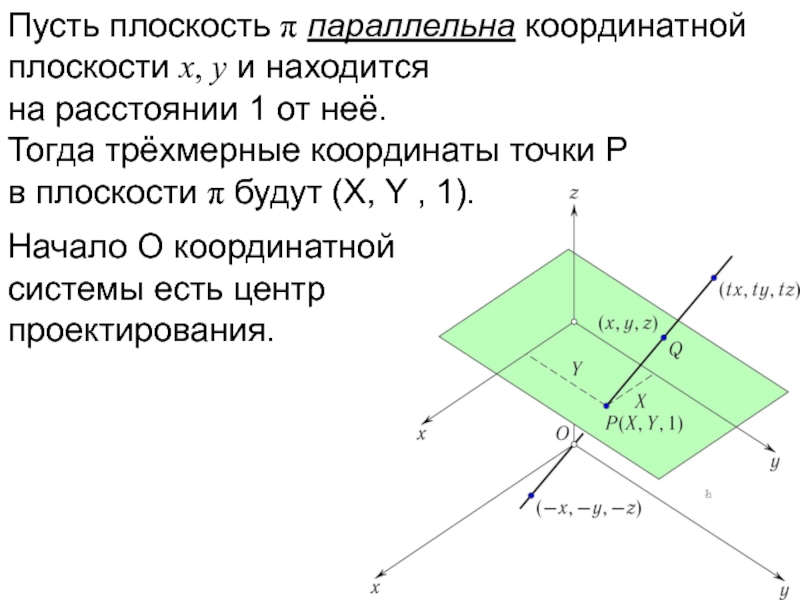
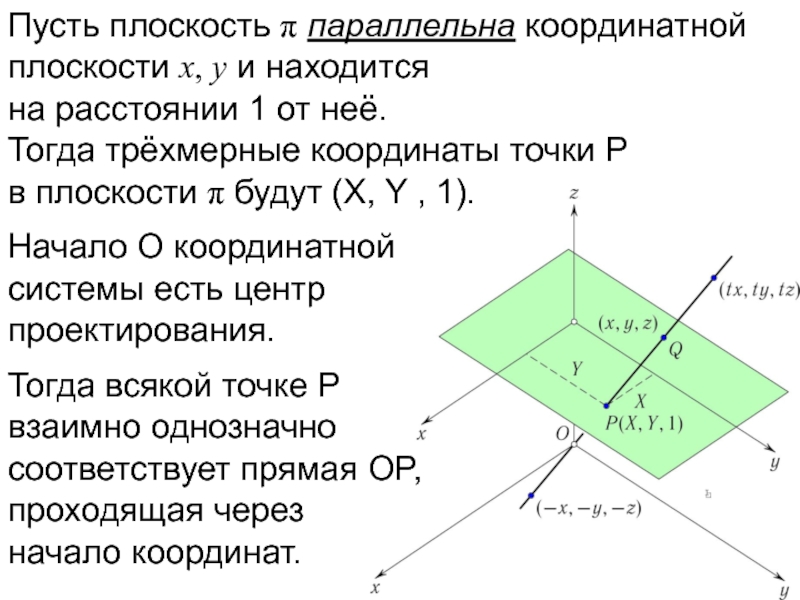
- 17. Пусть плоскость π параллельна координатной плоскости x,
- 18. Пусть плоскость π параллельна координатной плоскости x,
- 19. Пусть плоскость π параллельна координатной плоскости x,
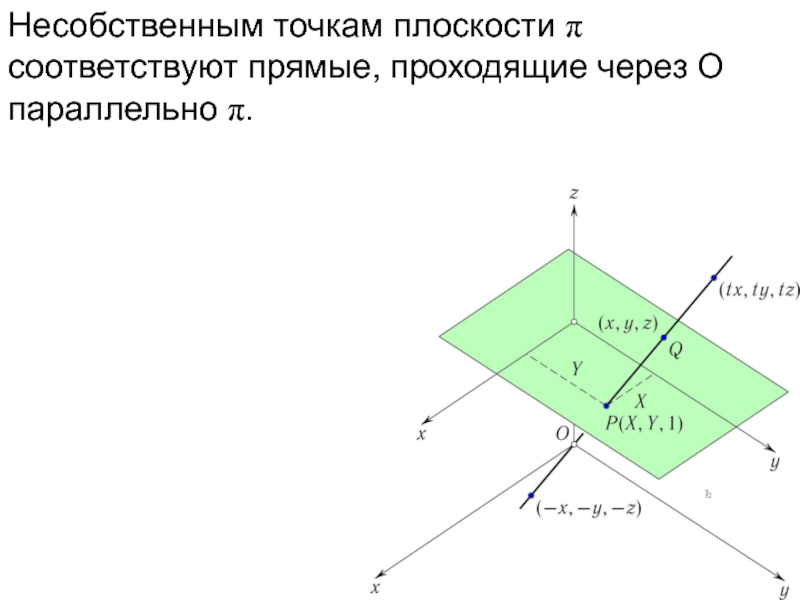
- 20. Несобственным точкам плоскости π соответствуют прямые, проходящие через O параллельно π.
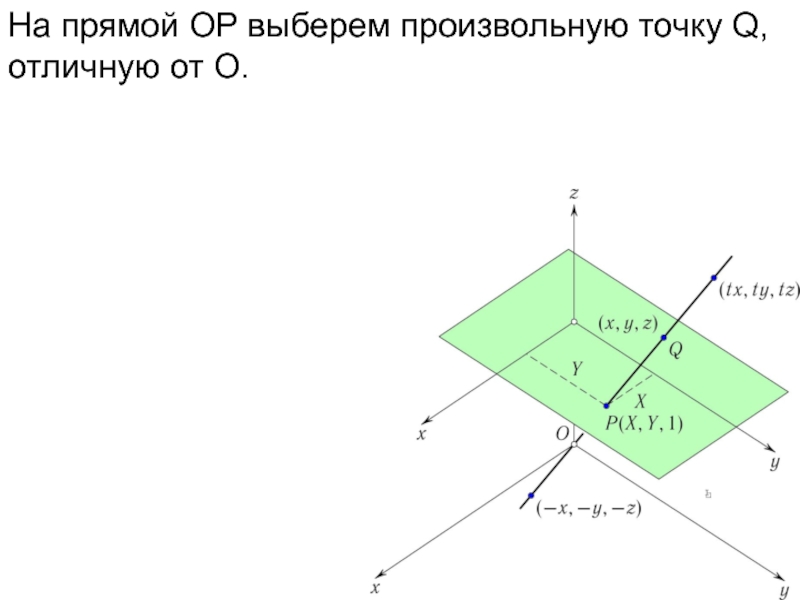
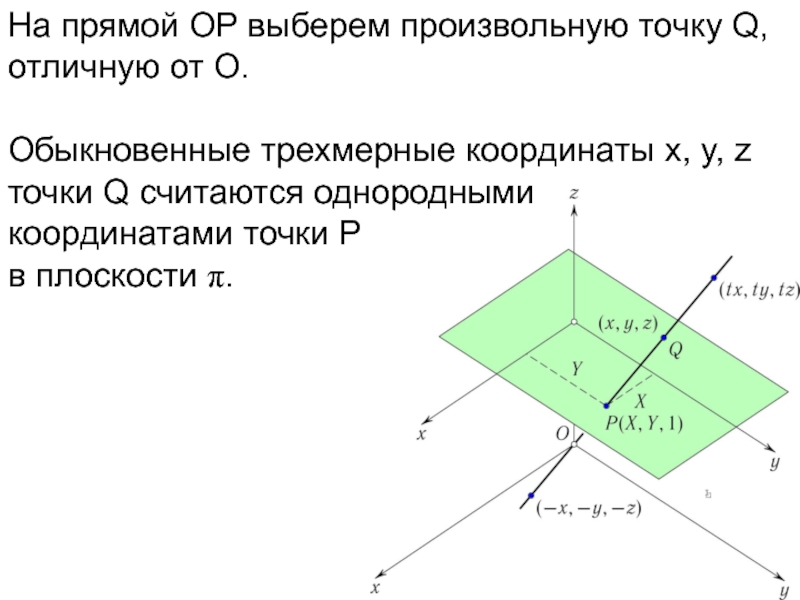
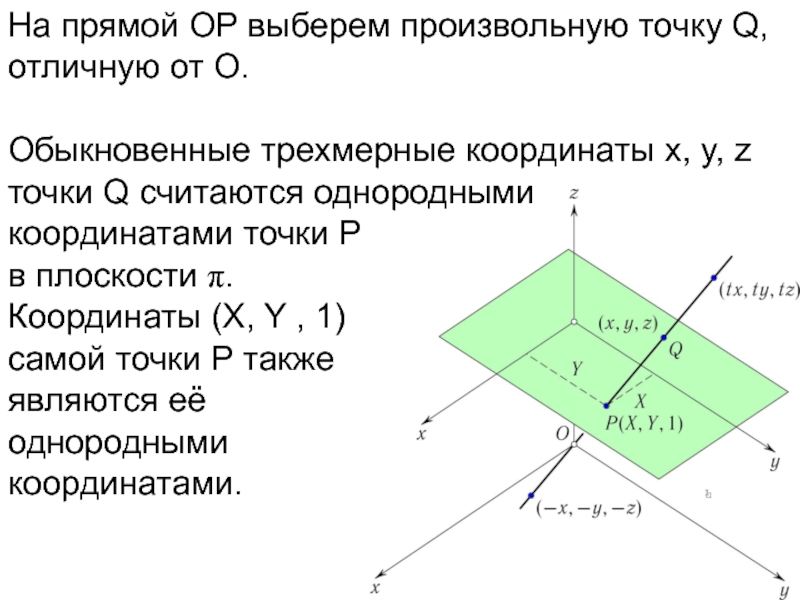
- 21. На прямой OP выберем произвольную точку Q, отличную от O.
- 22. На прямой OP выберем произвольную точку Q,
- 23. На прямой OP выберем произвольную точку Q,
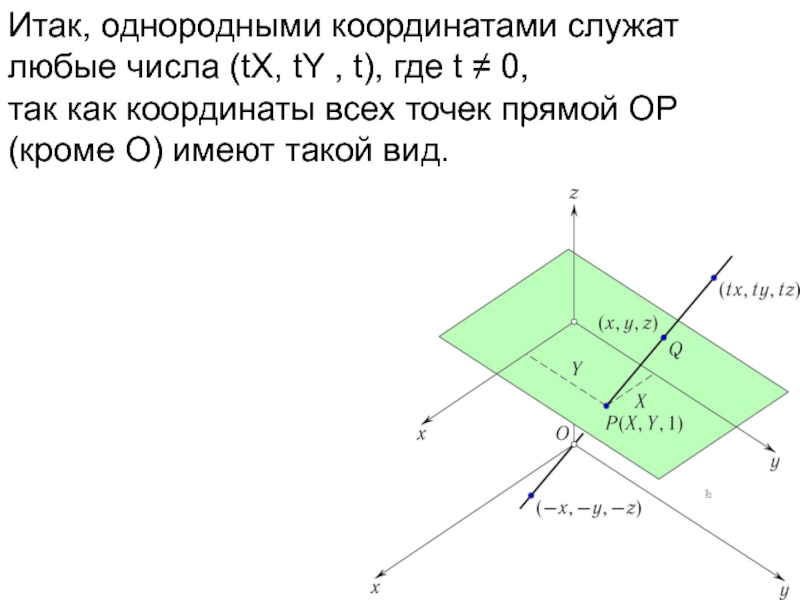
- 24. Итак, однородными координатами служат любые числа (tX,
- 25. Итак, однородными координатами служат любые числа (tX,
- 26. В системе однородных координат нужны три числа вместо двух для определения точки.
- 27. В системе однородных координат нужны три числа
- 28. В системе однородных координат нужны три числа
- 29. Несобственной точке P соответствует прямая, проходящая через
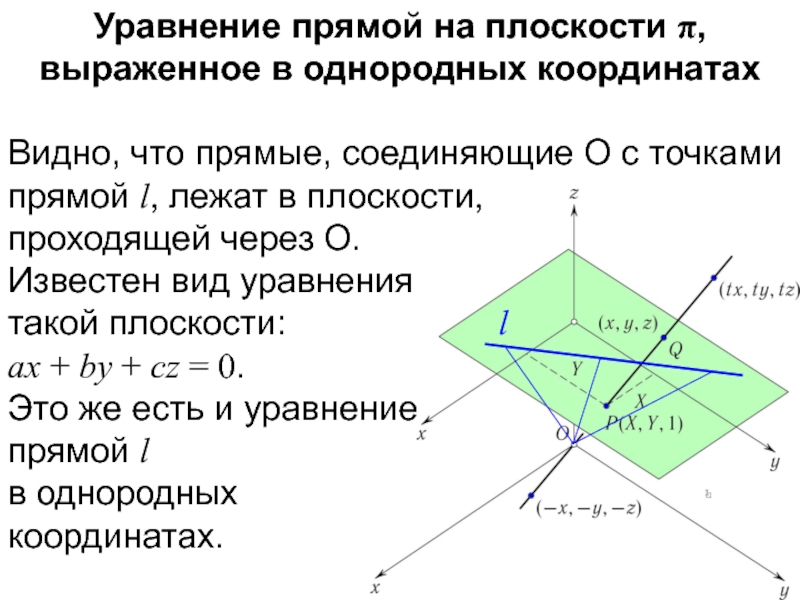
- 30. Уравнение прямой на плоскости π, выраженное в однородных координатах l
- 31. Уравнение прямой на плоскости π, выраженное в
- 32. Уравнение прямой на плоскости π, выраженное в
- 33. Уравнение прямой на плоскости π, выраженное в
- 34. Рассмотрим чисто аналитическое определение проективной плоскости.
- 35. Рассмотрим чисто аналитическое определение проективной плоскости.
- 36. Рассмотрим чисто аналитическое определение проективной плоскости.
- 37. Рассмотрим чисто аналитическое определение проективной плоскости.
- 38. Рассмотрим чисто аналитическое определение проективной плоскости.
- 39. Прямая линия в плоскости π состоит из
- 40. Прямая линия в плоскости π состоит из
- 41. Прямая линия в плоскости π состоит из
- 42. При произвольном t ≠ 0 тройка чисел
- 43. Эти определения полностью симметричны между точкой и
- 44. Эти определения полностью симметричны между точкой и
- 45. Эти определения полностью симметричны между точкой и
- 46. Например, тождество 2 · 3 + 1
- 47. Например, тождество 2 · 3 + 1
- 48. Например, тождество 2 · 3 + 1
- 49. Замечание: В евклидовой плоскости X, Y о
- 50. Замечание: В евклидовой плоскости X, Y о
- 51. Для перехода от однородных координат x, y,
- 52. Для перехода от однородных координат x, y,
- 53. l Уравнение aX + bY + c
- 54. Например, уравнение прямой 2x − 3y +
- 55. Например, уравнение прямой 2x − 3y +
- 56. Можно показать, что проективное преобразование, задается аналитически
- 57. Можно показать, что проективное преобразование, задается аналитически
- 58. 3. Треугольник цветов
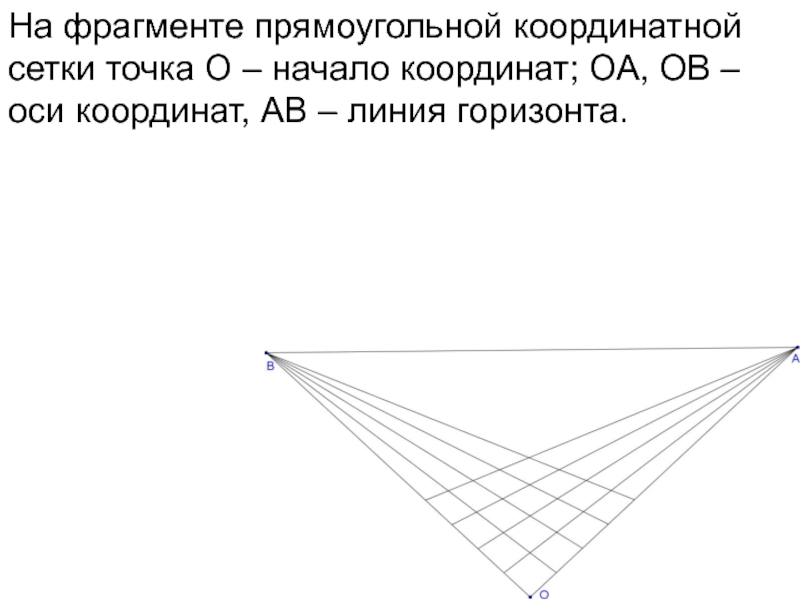
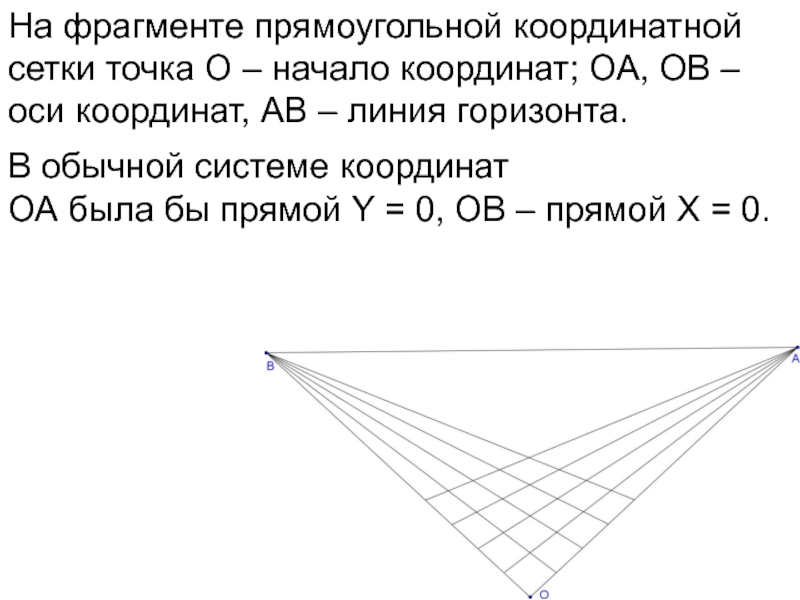
- 59. На фрагменте прямоугольной координатной сетки точка О
- 60. На фрагменте прямоугольной координатной сетки точка О
- 61. На фрагменте прямоугольной координатной сетки точка О
- 62. Линия горизонта АВ – прямая в бесконечности.
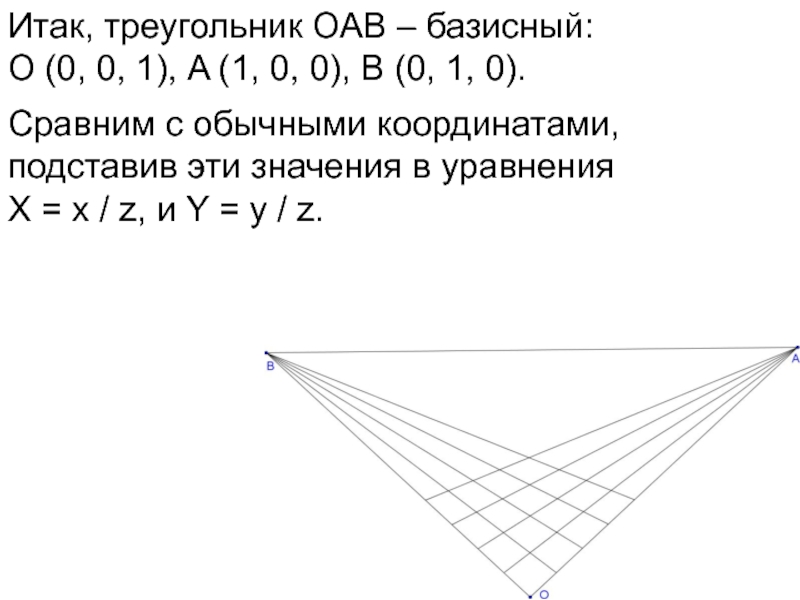
- 63. Итак, треугольник ОАВ – базисный: О (0,
- 64. Итак, треугольник ОАВ – базисный: О (0,
- 65. Итак, треугольник ОАВ – базисный: О (0,
- 66. Итак, треугольник ОАВ – базисный: О (0,
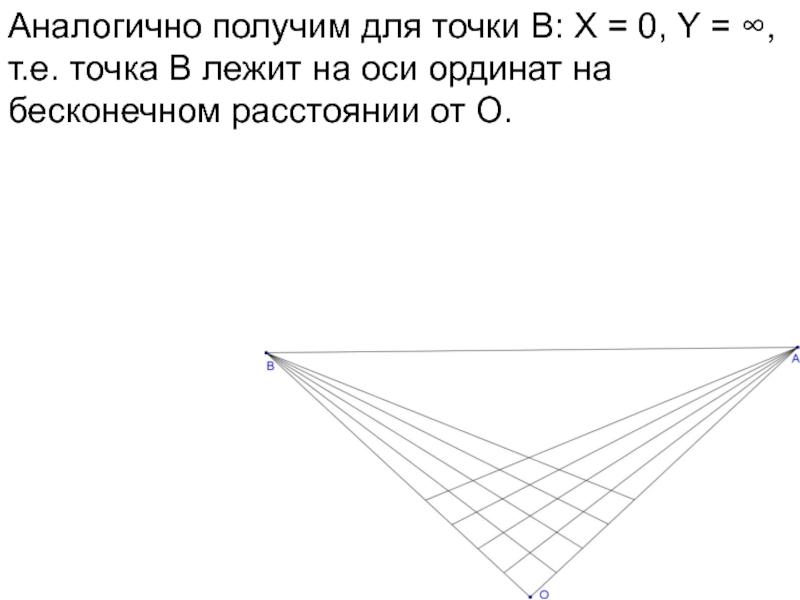
- 67. Аналогично получим для точки В: Х =
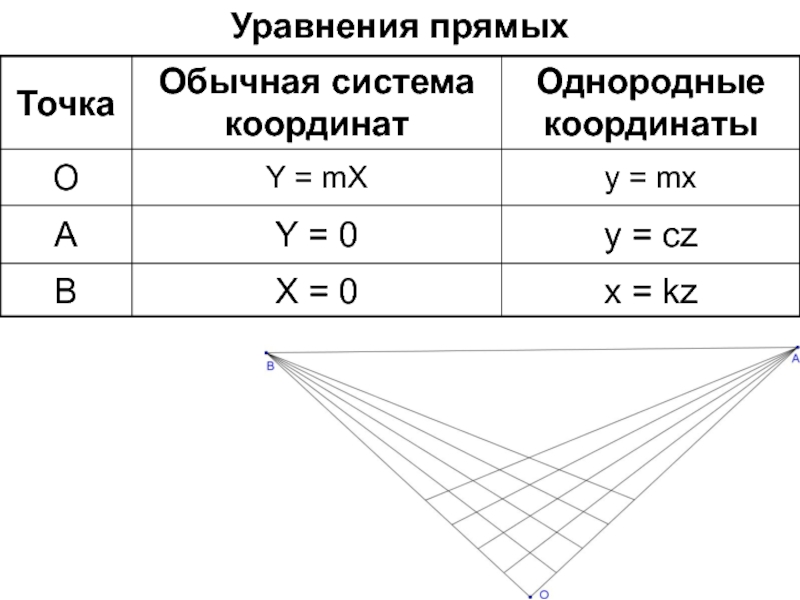
- 68. Уравнения прямых
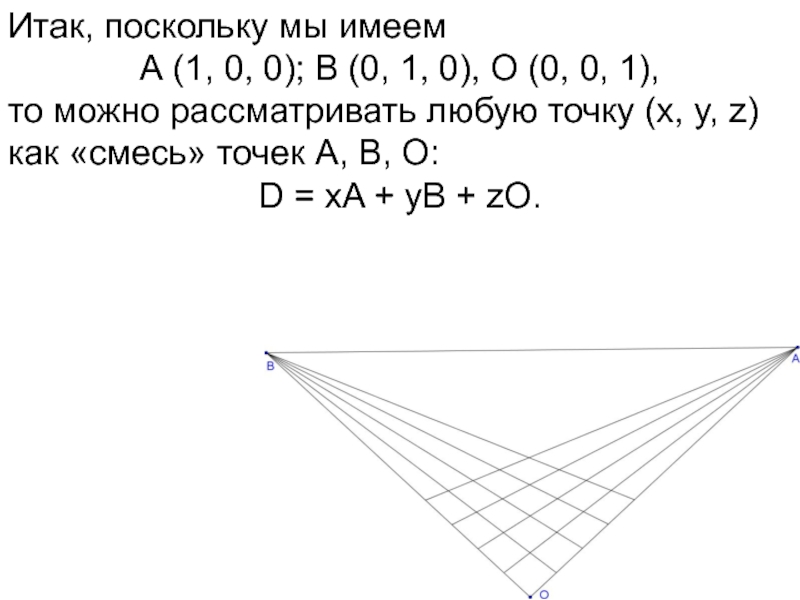
- 69. Итак, поскольку мы имеем А (1, 0,
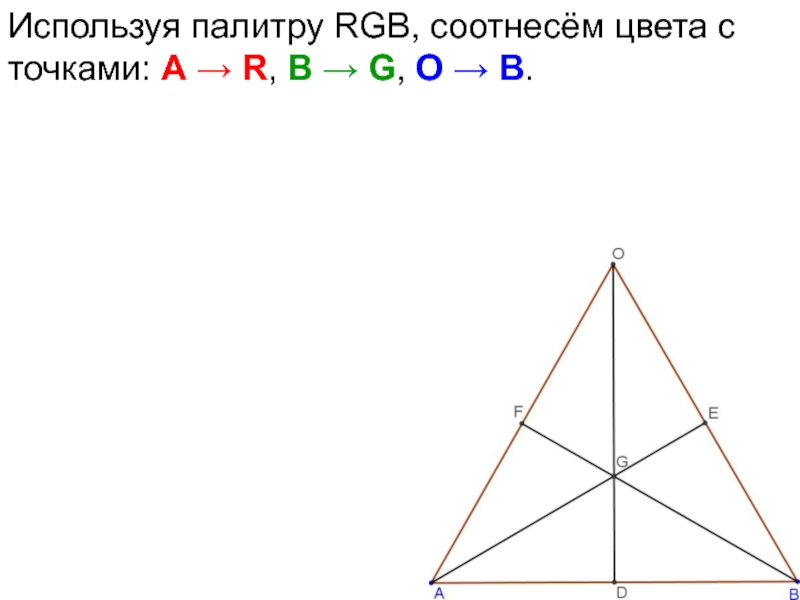
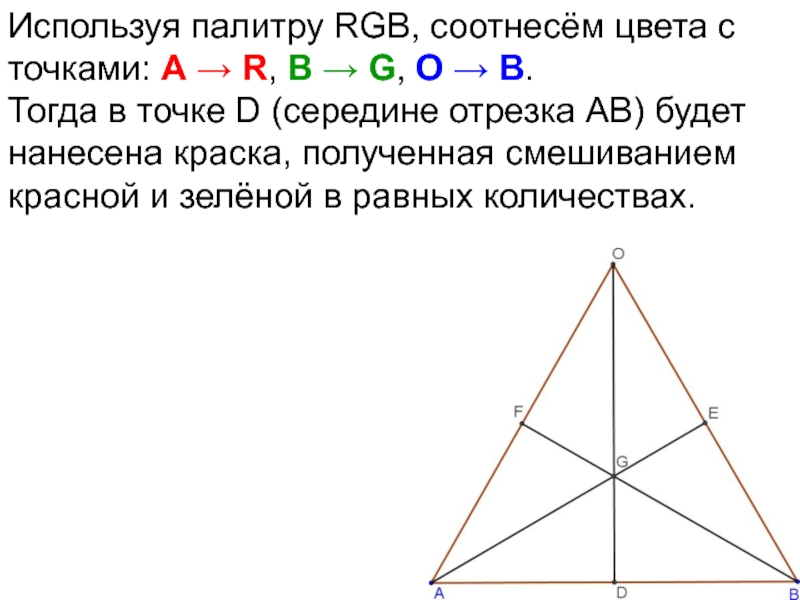
- 70. Используя палитру RGB, соотнесём цвета с точками:
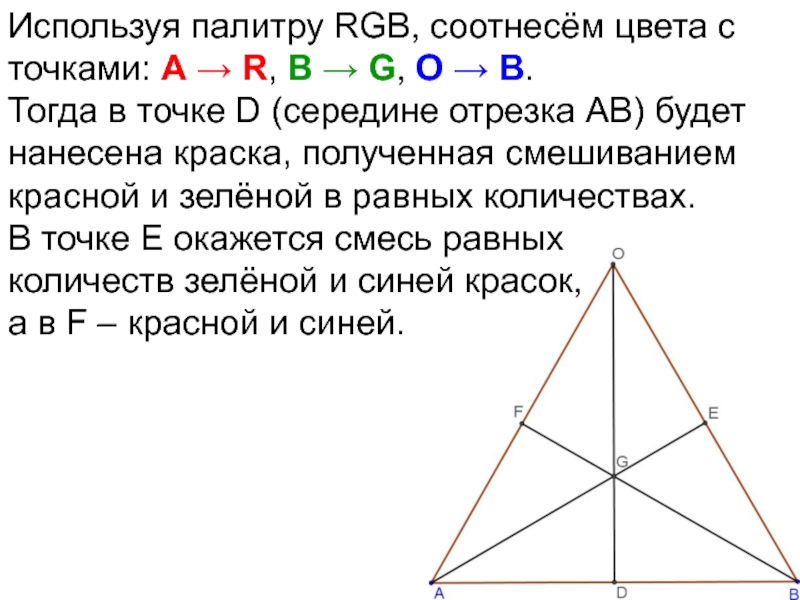
- 71. Используя палитру RGB, соотнесём цвета с точками:
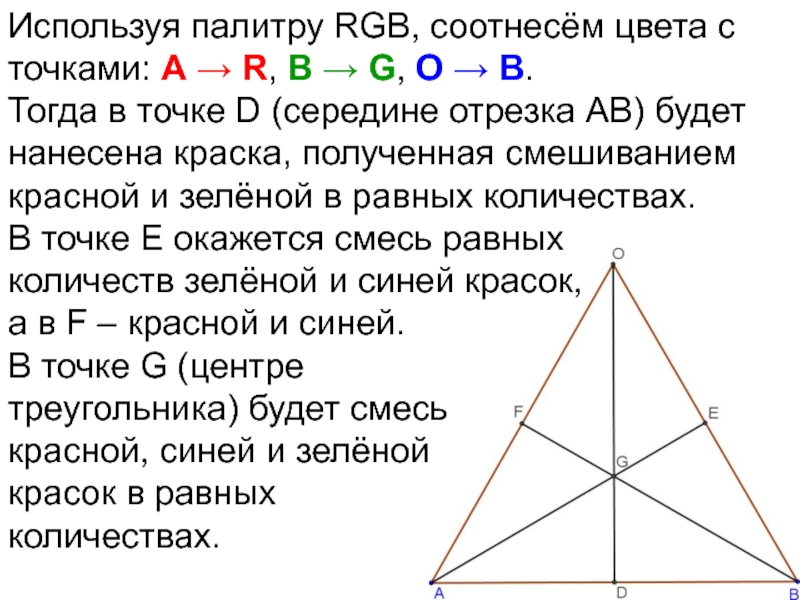
- 72. Используя палитру RGB, соотнесём цвета с точками:
- 73. Используя палитру RGB, соотнесём цвета с точками:
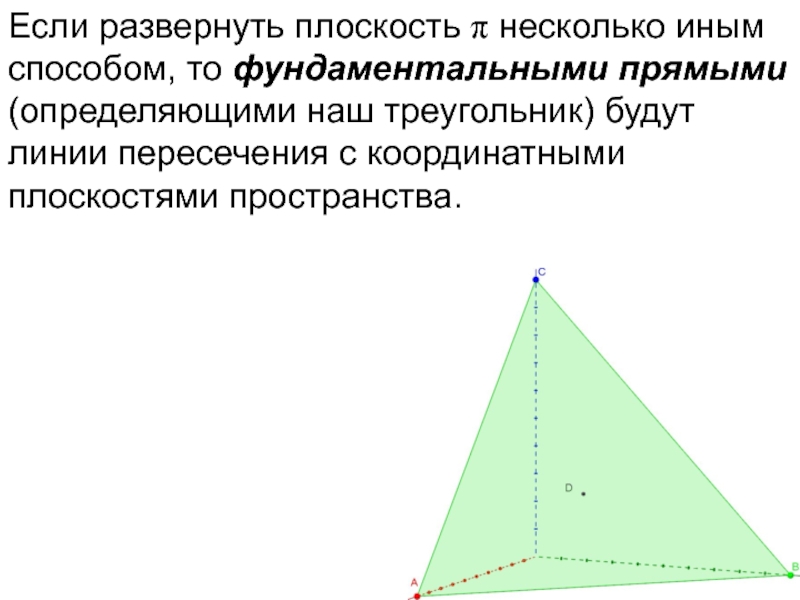
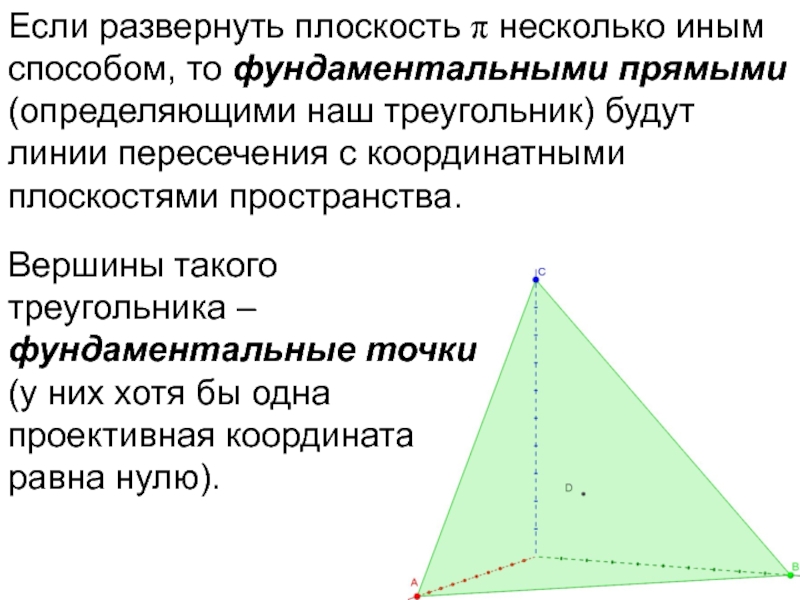
- 74. Если развернуть плоскость π несколько иным способом,
- 75. Если развернуть плоскость π несколько иным способом,
Слайд 3В аналитической геометрии
под «координатами»
геометрического объекта
понимается
любая совокупность чисел,
позволяющая
однозначно определить этот объект.
Слайд 4Примеры
1) Точка определяется
своими прямоугольными координатами x, y
или
своими полярными координатами r, ϕ.
Слайд 5Примеры
1) Точка определяется
своими прямоугольными координатами x, y
или
своими полярными координатами r, ϕ.
2) Треугольник определяется координатами трех вершин (шесть координат).
2) Треугольник определяется координатами трех вершин (шесть координат).
Слайд 6Примеры
1) Точка определяется
своими прямоугольными координатами x, y
или
своими полярными координатами r, ϕ.
2) Треугольник определяется координатами трех вершин (шесть координат).
3) Прямая линия в плоскости x, y – это геометрическое место всех точек P(x, y), координаты которых удовлетворяют уравнению ax + by + c = 0.
2) Треугольник определяется координатами трех вершин (шесть координат).
3) Прямая линия в плоскости x, y – это геометрическое место всех точек P(x, y), координаты которых удовлетворяют уравнению ax + by + c = 0.
Слайд 7Примеры
1) Точка определяется
своими прямоугольными координатами x, y
или
своими полярными координатами r, ϕ.
2) Треугольник определяется координатами трех вершин (шесть координат).
3) Прямая линия в плоскости x, y – это геометрическое место всех точек P(x, y), координаты которых удовлетворяют уравнению ax + by + c = 0. Поэтому три числа a, b, c можно назвать «координатами» этой прямой.
2) Треугольник определяется координатами трех вершин (шесть координат).
3) Прямая линия в плоскости x, y – это геометрическое место всех точек P(x, y), координаты которых удовлетворяют уравнению ax + by + c = 0. Поэтому три числа a, b, c можно назвать «координатами» этой прямой.
Слайд 8Примеры
1) Точка определяется
своими прямоугольными координатами x, y
или
своими полярными координатами r, ϕ.
2) Треугольник определяется координатами трех вершин (шесть координат).
3) Прямая линия в плоскости x, y – это геометрическое место всех точек P(x, y), координаты которых удовлетворяют уравнению ax + by + c = 0. Поэтому три числа a, b, c можно назвать «координатами» этой прямой.
4) Конические сечения: окружность, эллипс...
2) Треугольник определяется координатами трех вершин (шесть координат).
3) Прямая линия в плоскости x, y – это геометрическое место всех точек P(x, y), координаты которых удовлетворяют уравнению ax + by + c = 0. Поэтому три числа a, b, c можно назвать «координатами» этой прямой.
4) Конические сечения: окружность, эллипс...
Слайд 9То есть, отталкиваемся от множества чисел x,
всевозможных пар чисел (x, y),
троек
чисел (x, y, z) и т.д.
Слайд 10То есть, отталкиваемся от множества чисел x,
всевозможных пар чисел (x, y),
троек
чисел (x, y, z) и т.д.
Каждый такой элемент (число, пару, тройку...) называем точкой и можем, при необходимости, наглядно интерпретировать.
Каждый такой элемент (число, пару, тройку...) называем точкой и можем, при необходимости, наглядно интерпретировать.
Слайд 11То есть, отталкиваемся от множества чисел x,
всевозможных пар чисел (x, y),
троек
чисел (x, y, z) и т.д.
Каждый такой элемент (число, пару, тройку...) называем точкой и можем, при необходимости, наглядно интерпретировать.
Приходим к тому, что в физике называют фазовым пространством.
Каждый такой элемент (число, пару, тройку...) называем точкой и можем, при необходимости, наглядно интерпретировать.
Приходим к тому, что в физике называют фазовым пространством.
Слайд 12То есть, отталкиваемся от множества чисел x,
всевозможных пар чисел (x, y),
троек
чисел (x, y, z) и т.д.
Каждый такой элемент (число, пару, тройку...) называем точкой и можем, при необходимости, наглядно интерпретировать.
Приходим к тому, что в физике называют фазовым пространством.
То есть, мы можем уходить из чисто геометрического пространства.
Каждый такой элемент (число, пару, тройку...) называем точкой и можем, при необходимости, наглядно интерпретировать.
Приходим к тому, что в физике называют фазовым пространством.
То есть, мы можем уходить из чисто геометрического пространства.
Слайд 14Обыкновенная аналитическая геометрия:
прямоугольные координаты точки
на
плоскости – это снабжённые знаками
расстояния точки от двух
взаимно перпендикулярных осей.
Слайд 15Обыкновенная аналитическая геометрия:
прямоугольные координаты точки
на
плоскости – это снабжённые знаками
расстояния точки от двух
взаимно перпендикулярных осей.
В такой системе координат нет места для несобственных точек проективной плоскости.
В такой системе координат нет места для несобственных точек проективной плоскости.
Слайд 16Обыкновенная аналитическая геометрия:
прямоугольные координаты точки
на
плоскости – это снабжённые знаками
расстояния точки от двух
взаимно перпендикулярных осей.
В такой системе координат нет места для несобственных точек проективной плоскости.
Поэтому для использования аналитических методов в проективной геометрии необходимо найти координатную систему, которая включает несобственные точки наравне с обыкновенными.
В такой системе координат нет места для несобственных точек проективной плоскости.
Поэтому для использования аналитических методов в проективной геометрии необходимо найти координатную систему, которая включает несобственные точки наравне с обыкновенными.
Слайд 17Пусть плоскость π параллельна координатной плоскости x, y и находится
на расстоянии
1 от неё.
Тогда трёхмерные координаты точки P в плоскости π будут (X, Y , 1).
Тогда трёхмерные координаты точки P в плоскости π будут (X, Y , 1).
Слайд 18Пусть плоскость π параллельна координатной плоскости x, y и находится
на расстоянии
1 от неё.
Тогда трёхмерные координаты точки P в плоскости π будут (X, Y , 1).
Начало O координатной системы есть центр проектирования.
Тогда трёхмерные координаты точки P в плоскости π будут (X, Y , 1).
Начало O координатной системы есть центр проектирования.
Слайд 19Пусть плоскость π параллельна координатной плоскости x, y и находится
на расстоянии
1 от неё.
Тогда трёхмерные координаты точки P в плоскости π будут (X, Y , 1).
Начало O координатной системы есть центр проектирования.
Тогда всякой точке P взаимно однозначно соответствует прямая OP, проходящая через
начало координат.
Тогда трёхмерные координаты точки P в плоскости π будут (X, Y , 1).
Начало O координатной системы есть центр проектирования.
Тогда всякой точке P взаимно однозначно соответствует прямая OP, проходящая через
начало координат.
Слайд 22На прямой OP выберем произвольную точку Q, отличную от O.
Обыкновенные трехмерные
координаты x, y, z точки Q считаются однородными
координатами точки P в плоскости π.
координатами точки P в плоскости π.
Слайд 23На прямой OP выберем произвольную точку Q, отличную от O.
Обыкновенные трехмерные
координаты x, y, z точки Q считаются однородными
координатами точки P в плоскости π.
Координаты (X, Y , 1) самой точки P также являются её однородными координатами.
координатами точки P в плоскости π.
Координаты (X, Y , 1) самой точки P также являются её однородными координатами.
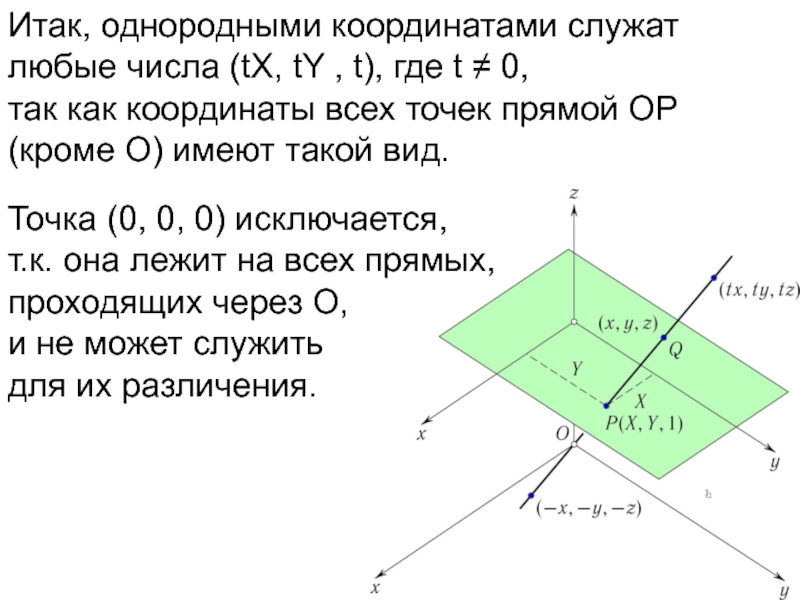
Слайд 24Итак, однородными координатами служат любые числа (tX, tY , t), где
t ≠ 0,
так как координаты всех точек прямой OP (кроме O) имеют такой вид.
так как координаты всех точек прямой OP (кроме O) имеют такой вид.
Слайд 25Итак, однородными координатами служат любые числа (tX, tY , t), где
t ≠ 0,
так как координаты всех точек прямой OP (кроме O) имеют такой вид.
Точка (0, 0, 0) исключается, т.к. она лежит на всех прямых, проходящих через O, и не может служить для их различения.
так как координаты всех точек прямой OP (кроме O) имеют такой вид.
Точка (0, 0, 0) исключается, т.к. она лежит на всех прямых, проходящих через O, и не может служить для их различения.
Слайд 27В системе однородных координат нужны три числа вместо двух для определения
точки.
Координаты точки определяются не однозначно, а с точностью до постоянного множителя.
Координаты точки определяются не однозначно, а с точностью до постоянного множителя.
Слайд 28В системе однородных координат нужны три числа вместо двух для определения
точки.
Координаты точки определяются не однозначно, а с точностью до постоянного множителя.
Но эта система охватывает обыкновенные и несобственные точки плоскости π.
Координаты точки определяются не однозначно, а с точностью до постоянного множителя.
Но эта система охватывает обыкновенные и несобственные точки плоскости π.
Слайд 29Несобственной точке P
соответствует прямая,
проходящая через O параллельно π.
Любая точка Q на
этой прямой
имеет координаты вида (x, y, 0).
Это значит, что однородные координаты несобственных точек плоскости π имеют вид (x, y, 0).
Это значит, что однородные координаты несобственных точек плоскости π имеют вид (x, y, 0).
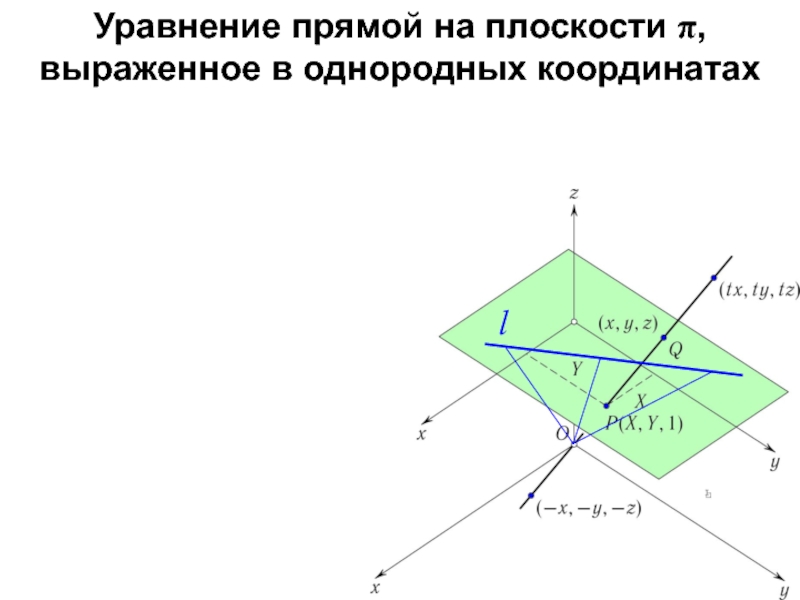
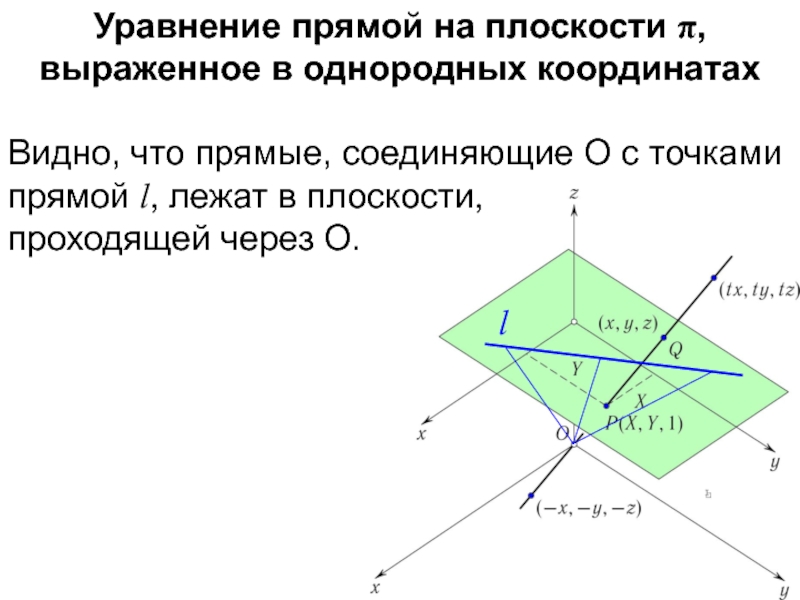
Слайд 31Уравнение прямой на плоскости π, выраженное в однородных координатах
Видно, что прямые,
соединяющие O с точками прямой l, лежат в плоскости,
проходящей через O.
проходящей через O.
l
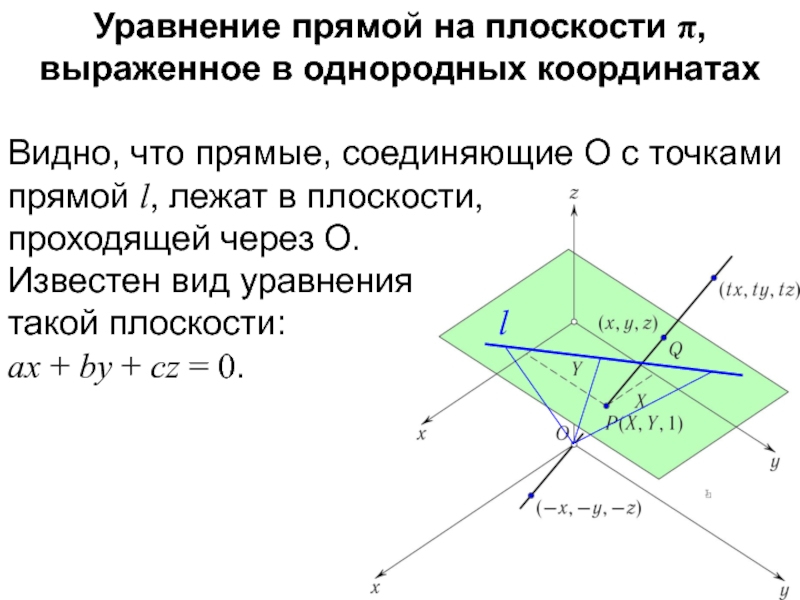
Слайд 32Уравнение прямой на плоскости π, выраженное в однородных координатах
Видно, что прямые,
соединяющие O с точками прямой l, лежат в плоскости,
проходящей через O.
Известен вид уравнения такой плоскости:
ax + by + cz = 0.
проходящей через O.
Известен вид уравнения такой плоскости:
ax + by + cz = 0.
l
Слайд 33Уравнение прямой на плоскости π, выраженное в однородных координатах
Видно, что прямые,
соединяющие O с точками прямой l, лежат в плоскости,
проходящей через O.
Известен вид уравнения такой плоскости:
ax + by + cz = 0.
Это же есть и уравнение прямой l в однородных координатах.
проходящей через O.
Известен вид уравнения такой плоскости:
ax + by + cz = 0.
Это же есть и уравнение прямой l в однородных координатах.
l
Слайд 35Рассмотрим чисто аналитическое определение проективной плоскости.
1) Точка есть тройка действительных
чисел
(x, y, z), из которых не все равны нулю.
Слайд 36Рассмотрим чисто аналитическое определение проективной плоскости.
1) Точка есть тройка действительных
чисел
(x, y, z), из которых не все равны нулю.
2) Две такие тройки (x1, y1, z1) и (x2, y2, z2)
определяют одну и ту же точку, если существует такое t ≠ 0, что
x2 = tx1, y2 = ty1, z2 = tz1.
2) Две такие тройки (x1, y1, z1) и (x2, y2, z2)
определяют одну и ту же точку, если существует такое t ≠ 0, что
x2 = tx1, y2 = ty1, z2 = tz1.
Слайд 37Рассмотрим чисто аналитическое определение проективной плоскости.
1) Точка есть тройка действительных
чисел
(x, y, z), из которых не все равны нулю.
2) Две такие тройки (x1, y1, z1) и (x2, y2, z2)
определяют одну и ту же точку, если существует такое t ≠ 0, что
x2 = tx1, y2 = ty1, z2 = tz1.
Потому эти координаты называются однородными.
2) Две такие тройки (x1, y1, z1) и (x2, y2, z2)
определяют одну и ту же точку, если существует такое t ≠ 0, что
x2 = tx1, y2 = ty1, z2 = tz1.
Потому эти координаты называются однородными.
Слайд 38Рассмотрим чисто аналитическое определение проективной плоскости.
1) Точка есть тройка действительных
чисел
(x, y, z), из которых не все равны нулю.
2) Две такие тройки (x1, y1, z1) и (x2, y2, z2)
определяют одну и ту же точку, если существует такое t ≠ 0, что
x2 = tx1, y2 = ty1, z2 = tz1.
Потому эти координаты называются однородными.
3) Точка (x, y, z) обыкновенная, если z ≠ 0, и несобственная, если z = 0.
2) Две такие тройки (x1, y1, z1) и (x2, y2, z2)
определяют одну и ту же точку, если существует такое t ≠ 0, что
x2 = tx1, y2 = ty1, z2 = tz1.
Потому эти координаты называются однородными.
3) Точка (x, y, z) обыкновенная, если z ≠ 0, и несобственная, если z = 0.
Слайд 39Прямая линия в плоскости π состоит из всех точек (x, y, z),
удовлетворяющих уравнению вида
ax + by + cz = 0,
где a, b, c – постоянные числа, не все равные нулю.
ax + by + cz = 0,
где a, b, c – постоянные числа, не все равные нулю.
Слайд 40Прямая линия в плоскости π состоит из всех точек (x, y, z),
удовлетворяющих уравнению вида
ax + by + cz = 0,
где a, b, c – постоянные числа, не все равные нулю.
Несобственные точки плоскости π удовлетворяют уравнению z = 0.
ax + by + cz = 0,
где a, b, c – постоянные числа, не все равные нулю.
Несобственные точки плоскости π удовлетворяют уравнению z = 0.
Слайд 41Прямая линия в плоскости π состоит из всех точек (x, y, z),
удовлетворяющих уравнению вида
ax + by + cz = 0,
где a, b, c – постоянные числа, не все равные нулю.
Несобственные точки плоскости π удовлетворяют уравнению z = 0.
Это уравнение несобственной прямой.
ax + by + cz = 0,
где a, b, c – постоянные числа, не все равные нулю.
Несобственные точки плоскости π удовлетворяют уравнению z = 0.
Это уравнение несобственной прямой.
Слайд 42При произвольном t ≠ 0 тройка чисел (ta, tb, tc) есть
координаты той же прямой, поскольку уравнение
(ta)x + (tb)y + (tc)z = 0
удовлетворяется теми же координатными тройками (x, y, z), что и уравнение
ax + by + cz = 0.
(ta)x + (tb)y + (tc)z = 0
удовлетворяется теми же координатными тройками (x, y, z), что и уравнение
ax + by + cz = 0.
Слайд 43Эти определения полностью симметричны между точкой и прямой:
они обе определяются тройкой
чисел – однородными координатами (u, v, w).
Слайд 44Эти определения полностью симметричны между точкой и прямой:
они обе определяются тройкой
чисел – однородными координатами (u, v, w).
Условие того, что точка (x, y, z) лежит на прямой (a, b, c), выражается равенством
ax + by + cz = 0.
Условие того, что точка (x, y, z) лежит на прямой (a, b, c), выражается равенством
ax + by + cz = 0.
Слайд 45Эти определения полностью симметричны между точкой и прямой:
они обе определяются тройкой
чисел – однородными координатами (u, v, w).
Условие того, что точка (x, y, z) лежит на прямой (a, b, c), выражается равенством
ax + by + cz = 0.
Это же есть условие того, что точка с координатами (a, b, c) лежит на прямой с координатами (x, y, z).
Условие того, что точка (x, y, z) лежит на прямой (a, b, c), выражается равенством
ax + by + cz = 0.
Это же есть условие того, что точка с координатами (a, b, c) лежит на прямой с координатами (x, y, z).
Слайд 46Например, тождество
2 · 3 + 1 · 4 + (−5) ·
2 = 0
означает, что точка (3, 4, 2) лежит на прямой (2, 1, −5), и что точка (2, 1, −5) лежит на прямой (3, 4, 2).
означает, что точка (3, 4, 2) лежит на прямой (2, 1, −5), и что точка (2, 1, −5) лежит на прямой (3, 4, 2).
Слайд 47Например, тождество
2 · 3 + 1 · 4 + (−5) ·
2 = 0
означает, что точка (3, 4, 2) лежит на прямой (2, 1, −5), и что точка (2, 1, −5) лежит на прямой (3, 4, 2).
Эта симметрия есть основа двойственности «точка ↔ прямая» в проективной геометрии:
означает, что точка (3, 4, 2) лежит на прямой (2, 1, −5), и что точка (2, 1, −5) лежит на прямой (3, 4, 2).
Эта симметрия есть основа двойственности «точка ↔ прямая» в проективной геометрии:
Слайд 48Например, тождество
2 · 3 + 1 · 4 + (−5) ·
2 = 0
означает, что точка (3, 4, 2) лежит на прямой (2, 1, −5), и что точка (2, 1, −5) лежит на прямой (3, 4, 2).
Эта симметрия есть основа двойственности «точка ↔ прямая» в проективной геометрии: всякое соотношение между точками и прямыми становится некоторым соотношением между прямыми и точками, если координаты точек считать координатами прямых, а координаты прямых – координатами точек.
означает, что точка (3, 4, 2) лежит на прямой (2, 1, −5), и что точка (2, 1, −5) лежит на прямой (3, 4, 2).
Эта симметрия есть основа двойственности «точка ↔ прямая» в проективной геометрии: всякое соотношение между точками и прямыми становится некоторым соотношением между прямыми и точками, если координаты точек считать координатами прямых, а координаты прямых – координатами точек.
Слайд 49Замечание:
В евклидовой плоскости X, Y о двойственности не может быть речи,
т.к. уравнение прямой в обыкновенных
координатах
aX + bY + c = 0
несимметрично относительно X, Y и a, b, c.
координатах
aX + bY + c = 0
несимметрично относительно X, Y и a, b, c.
Слайд 50Замечание:
В евклидовой плоскости X, Y о двойственности не может быть речи,
т.к. уравнение прямой в обыкновенных
координатах
aX + bY + c = 0
несимметрично относительно X, Y и a, b, c.
Только включение в рассмотрение
бесконечно удаленных элементов
(точек и прямой)
обеспечивает применимость
принципа двойственности.
координатах
aX + bY + c = 0
несимметрично относительно X, Y и a, b, c.
Только включение в рассмотрение
бесконечно удаленных элементов
(точек и прямой)
обеспечивает применимость
принципа двойственности.
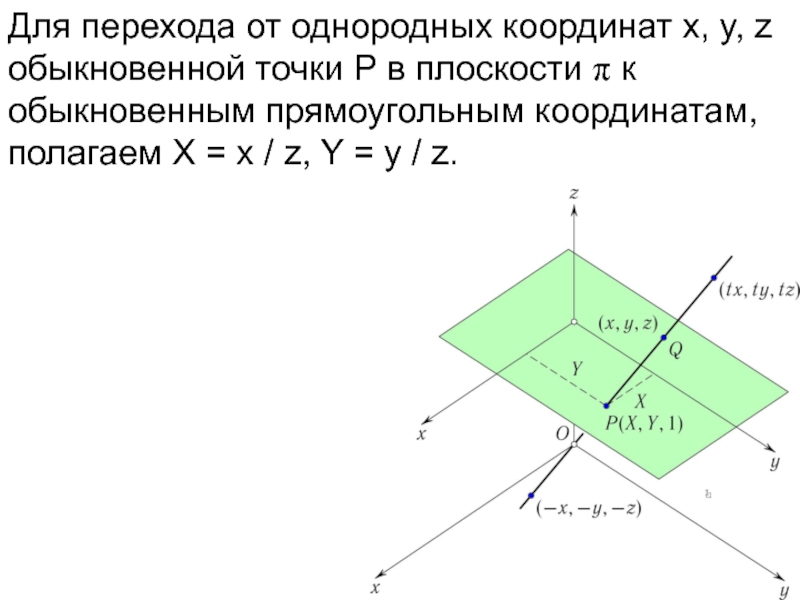
Слайд 51Для перехода от однородных координат x, y, z обыкновенной точки P
в плоскости π к обыкновенным прямоугольным координатам, полагаем X = x / z, Y = y / z.
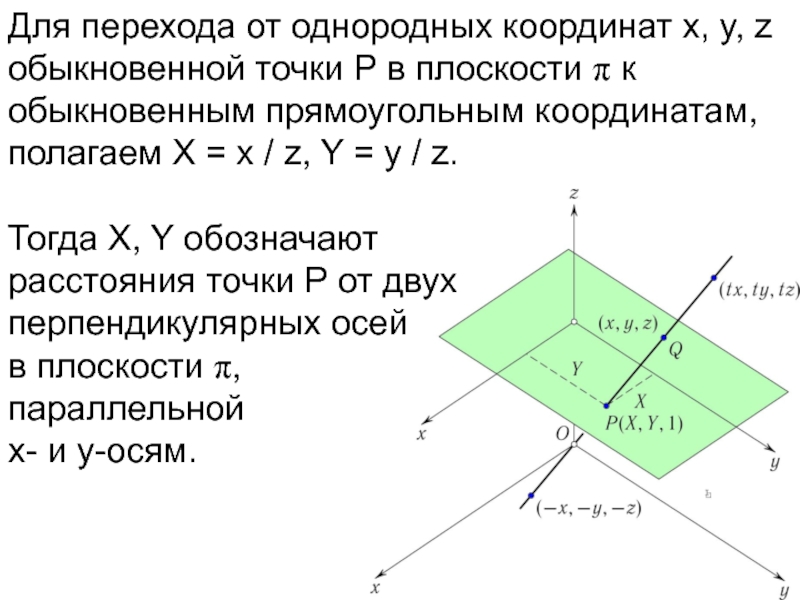
Слайд 52Для перехода от однородных координат x, y, z обыкновенной точки P
в плоскости π к обыкновенным прямоугольным координатам, полагаем X = x / z, Y = y / z.
Тогда X, Y обозначают
расстояния точки P от двух
перпендикулярных осей
в плоскости π,
параллельной
x- и y-осям.
Тогда X, Y обозначают
расстояния точки P от двух
перпендикулярных осей
в плоскости π,
параллельной
x- и y-осям.
Слайд 53l
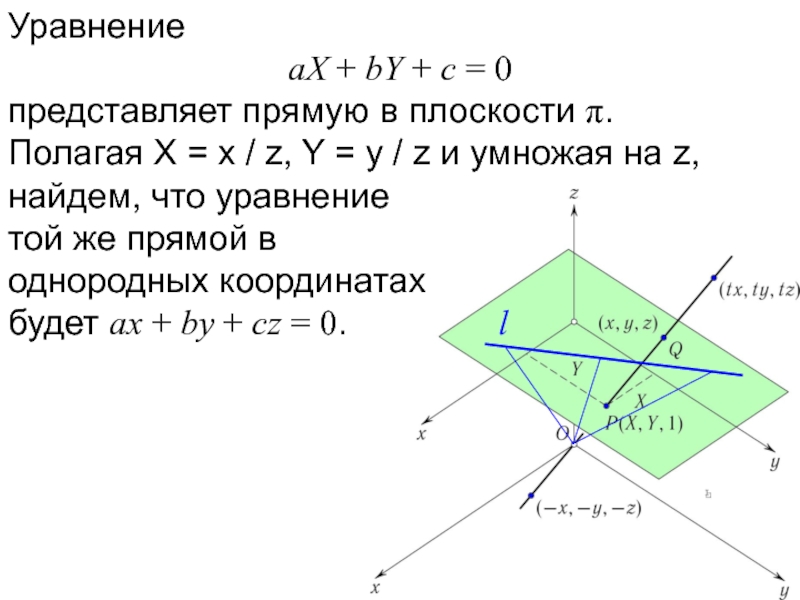
Уравнение
aX + bY + c = 0
представляет прямую в плоскости π.
Полагая
X = x / z, Y = y / z и умножая на z,
найдем, что уравнение той же прямой в однородных координатах будет ax + by + cz = 0.
найдем, что уравнение той же прямой в однородных координатах будет ax + by + cz = 0.
Слайд 54Например, уравнение прямой
2x − 3y + z = 0
в обыкновенных прямоугольных
координатах X, Y примет вид
2X − 3Y + 1 = 0.
2X − 3Y + 1 = 0.
Слайд 55Например, уравнение прямой
2x − 3y + z = 0
в обыкновенных прямоугольных
координатах X, Y примет вид
2X − 3Y + 1 = 0.
Замечание. Последнему уравнению несобственная точка рассматриваемой прямой с однородными координатами (3, 2, 0) уже не отвечает.
2X − 3Y + 1 = 0.
Замечание. Последнему уравнению несобственная точка рассматриваемой прямой с однородными координатами (3, 2, 0) уже не отвечает.
Слайд 56Можно показать, что проективное преобразование, задается аналитически системой линейных уравнений
связывающих однородные
координаты x', y', z�' точек в плоскости π' с однородными координатами x, y, z точек в плоскости π.
Слайд 57Можно показать, что проективное преобразование, задается аналитически системой линейных уравнений
связывающих однородные
координаты x', y', z�' точек в плоскости π' с однородными координатами x, y, z точек в плоскости π.
Тогда теоремы проективной геометрии становятся теоремами о поведении числовых троек (x, y, z) при таких преобразованиях.
Тогда теоремы проективной геометрии становятся теоремами о поведении числовых троек (x, y, z) при таких преобразованиях.
Слайд 59На фрагменте прямоугольной координатной сетки точка О – начало координат; ОА,
ОВ – оси координат, АВ – линия горизонта.
Слайд 60На фрагменте прямоугольной координатной сетки точка О – начало координат; ОА,
ОВ – оси координат, АВ – линия горизонта.
В обычной системе координат ОА была бы прямой Y = 0, ОВ – прямой Х = 0.
В обычной системе координат ОА была бы прямой Y = 0, ОВ – прямой Х = 0.
Слайд 61На фрагменте прямоугольной координатной сетки точка О – начало координат; ОА,
ОВ – оси координат, АВ – линия горизонта.
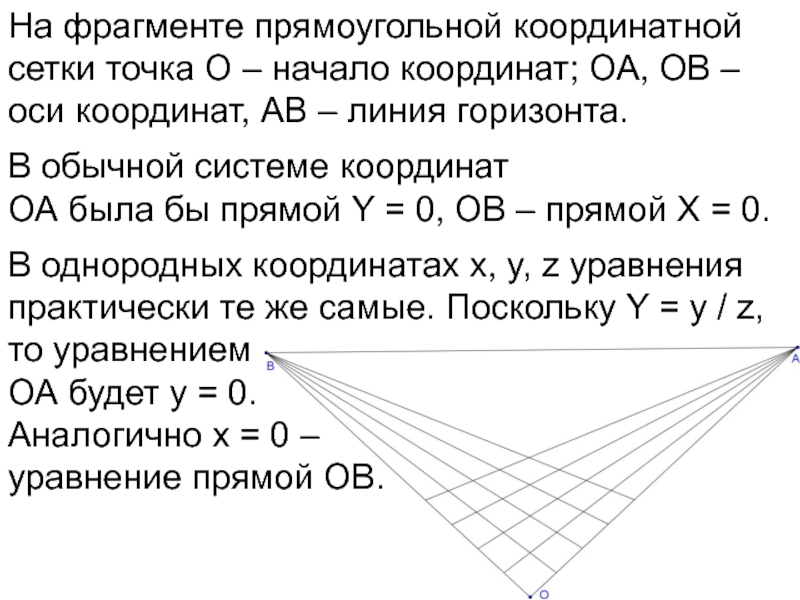
В обычной системе координат ОА была бы прямой Y = 0, ОВ – прямой X = 0.
В однородных координатах x, y, z уравнения практически те же самые. Поскольку Y = y / z, то уравнением ОА будет y = 0. Аналогично x = 0 – уравнение прямой ОВ.
В обычной системе координат ОА была бы прямой Y = 0, ОВ – прямой X = 0.
В однородных координатах x, y, z уравнения практически те же самые. Поскольку Y = y / z, то уравнением ОА будет y = 0. Аналогично x = 0 – уравнение прямой ОВ.
Слайд 62Линия горизонта АВ – прямая в бесконечности. Её уравнение – z
= 0.
Итак, имеем трехстороннюю симметрию (в отличие от обычной координатной сетки с двусторонней симметрией).
То есть, имеем три равноправные прямые: ОВ (x = 0); ОА (y = 0); АВ (z = 0).
Итак, имеем трехстороннюю симметрию (в отличие от обычной координатной сетки с двусторонней симметрией).
То есть, имеем три равноправные прямые: ОВ (x = 0); ОА (y = 0); АВ (z = 0).
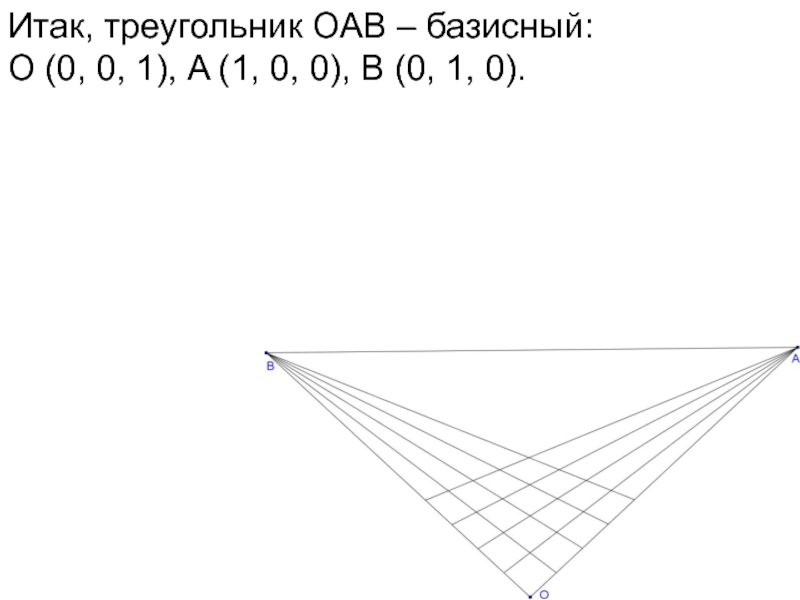
Слайд 64Итак, треугольник ОАВ – базисный: О (0, 0, 1), A (1, 0,
0), В (0, 1, 0).
Сравним с обычными координатами, подставив эти значения в уравнения X = x / z, и Y = y / z.
Сравним с обычными координатами, подставив эти значения в уравнения X = x / z, и Y = y / z.
Слайд 65Итак, треугольник ОАВ – базисный: О (0, 0, 1), A (1, 0,
0), В (0, 1, 0).
Сравним с обычными координатами, подставив эти значения в уравнения X = x / z, и Y = y / z.
Для точки О затруднений нет, т.к. Х = 0, Y = 0.
Сравним с обычными координатами, подставив эти значения в уравнения X = x / z, и Y = y / z.
Для точки О затруднений нет, т.к. Х = 0, Y = 0.
Слайд 66Итак, треугольник ОАВ – базисный: О (0, 0, 1), A (1, 0,
0), В (0, 1, 0).
Сравним с обычными координатами, подставив эти значения в уравнения X = x / z, и Y = y / z.
Для точки О затруднений нет, т.к. Х = 0, Y = 0.
Для точки А имеем X = ∞, Y = 0. Она должна находиться на оси Ох на бесконечно большом расстоянии от начала координат. Она там и находится.
Сравним с обычными координатами, подставив эти значения в уравнения X = x / z, и Y = y / z.
Для точки О затруднений нет, т.к. Х = 0, Y = 0.
Для точки А имеем X = ∞, Y = 0. Она должна находиться на оси Ох на бесконечно большом расстоянии от начала координат. Она там и находится.
Слайд 67Аналогично получим для точки В: Х = 0, Y = ∞,
т.е. точка В лежит на оси ординат на бесконечном расстоянии от О.
Слайд 69Итак, поскольку мы имеем
А (1, 0, 0); В (0, 1, 0),
О (0, 0, 1),
то можно рассматривать любую точку (x, y, z) как «смесь» точек А, В, О:
D = xA + yB + zO.
то можно рассматривать любую точку (x, y, z) как «смесь» точек А, В, О:
D = xA + yB + zO.
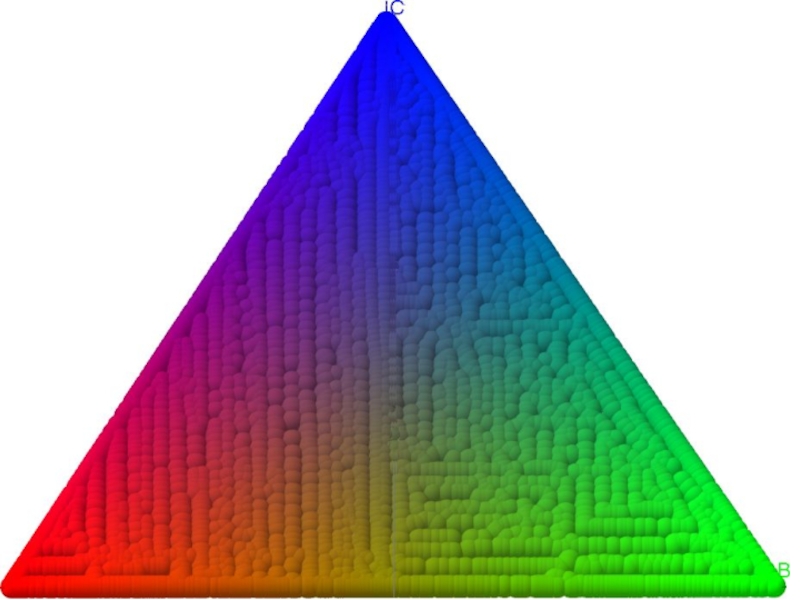
Слайд 71Используя палитру RGB, соотнесём цвета с точками: А → R, В
→ G, О → B.
Тогда в точке D (середине отрезка АВ) будет нанесена краска, полученная смешиванием красной и зелёной в равных количествах.
Слайд 72Используя палитру RGB, соотнесём цвета с точками: А → R, В
→ G, О → B.
Тогда в точке D (середине отрезка АВ) будет нанесена краска, полученная смешиванием красной и зелёной в равных количествах.
В точке Е окажется смесь равных
количеств зелёной и синей красок,
а в F – красной и синей.
Слайд 73Используя палитру RGB, соотнесём цвета с точками: А → R, В
→ G, О → B.
Тогда в точке D (середине отрезка АВ) будет нанесена краска, полученная смешиванием красной и зелёной в равных количествах.
В точке Е окажется смесь равных
количеств зелёной и синей красок,
а в F – красной и синей.
В точке G (центре
треугольника) будет смесь
красной, синей и зелёной
красок в равных
количествах.
Слайд 74Если развернуть плоскость π несколько иным способом, то фундаментальными прямыми (определяющими
наш треугольник) будут линии пересечения с координатными плоскостями пространства.
Слайд 75Если развернуть плоскость π несколько иным способом, то фундаментальными прямыми (определяющими
наш треугольник) будут линии пересечения с координатными плоскостями пространства.
Вершины такого треугольника – фундаментальные точки (у них хотя бы одна проективная координата равна нулю).
Вершины такого треугольника – фундаментальные точки (у них хотя бы одна проективная координата равна нулю).