- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 06. Основные понятия проективной геометрии (продолжение) презентация
Содержание
- 1. Лекция 06. Основные понятия проективной геометрии (продолжение)
- 2. 1. Некоторые воспоминания
- 5. Проективные свойства (инварианты)
- 6. Проективные свойства (инварианты) инцидентность коллинеарность конкуррентность
- 7. 2. Принцип двойственности
- 8. Взаимно-двойственные элементы точка прямая
- 9. Взаимно-двойственные элементы точка
- 10. Пример замены «точка ↔ прямая»
- 11. Пример замены «точка ↔ прямая»
- 12. Пример замены «точка ↔ прямая»
- 13. Пример замены «точка ↔ прямая»
- 14. Пример замены «точка ↔ прямая»
- 15. Принцип двойственности Из каждого проективного
- 16. Принцип двойственности Две фигуры взаимно
- 17. Принцип двойственности Две теоремы взаимно
- 18. Принцип двойственности Явление двойственности резко
- 19. Принцип двойственности Явление двойственности резко
- 20. Принцип двойственности Каждой верной теореме
- 21. Принцип двойственности Каждой верной теореме
- 22. Перспективность относительно точки Есть две
- 23. Перспективность относительно точки Есть две
- 24. Перспективность относительно точки Есть две
- 25. Перспективность относительно прямой Есть две
- 26. Перспективность относительно прямой Есть две
- 27. Перспективность относительно прямой Есть две
- 28. Экзотические случаи Ось перспективы – несобственная прямая
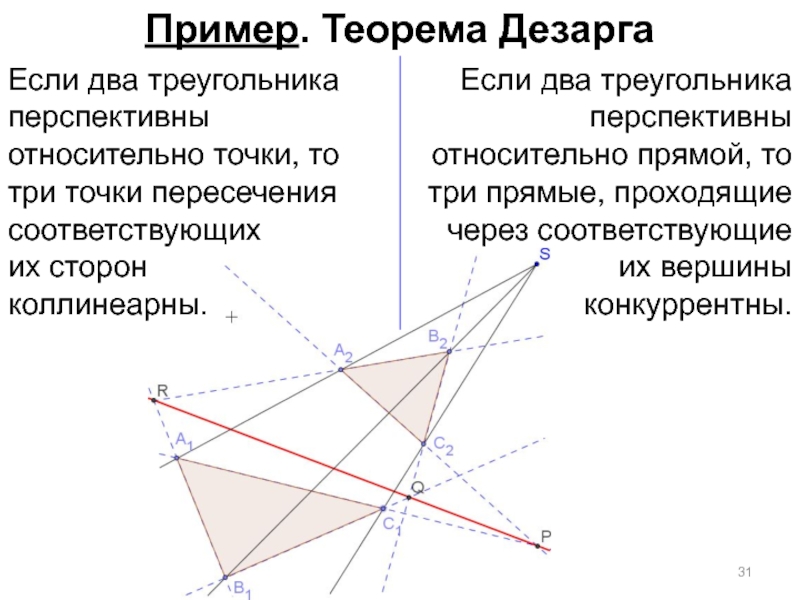
- 29. Пример. Теорема Дезарга
- 30. Пример. Теорема Дезарга
- 31. Пример. Теорема Дезарга
- 32. Пример. Теорема Дезарга
- 33. Пример. Теорема Дезарга
- 34. Вспомогательные теоремы
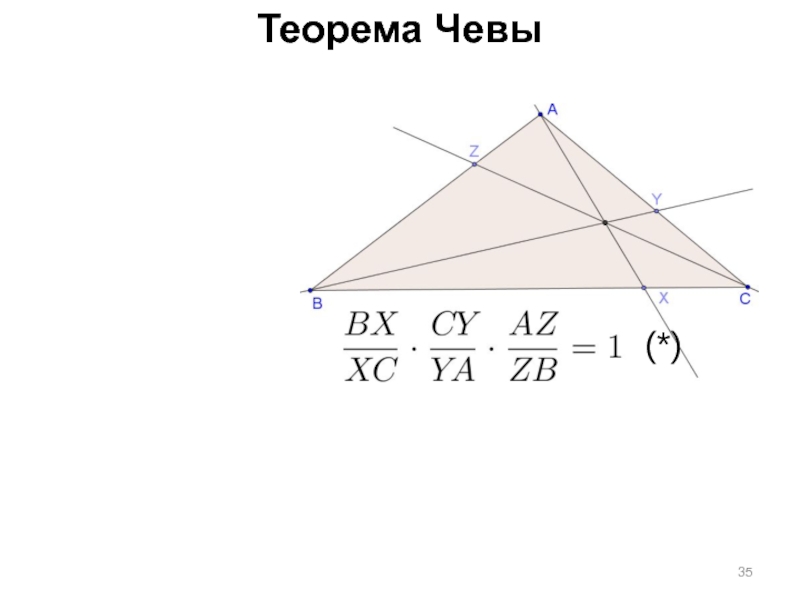
- 35. Теорема Чевы (*)
- 36. Теорема Чевы Если три чевианы AX, BY,
- 37. Теорема Чевы Если три чевианы AX, BY,
- 38. Теорема Менелая (*)
- 39. Теорема Менелая Если точки X, Y, Z,
- 40. Теорема Менелая Если точки X, Y, Z,
- 41. Резюме Теорема Чевы – критерий конкуррентности. Теорема Менелая – критерий коллинеарности.
- 42. Домашнее задание Доказать теоремы Чевы и
- 43. Теорема Чевы (доказательство)
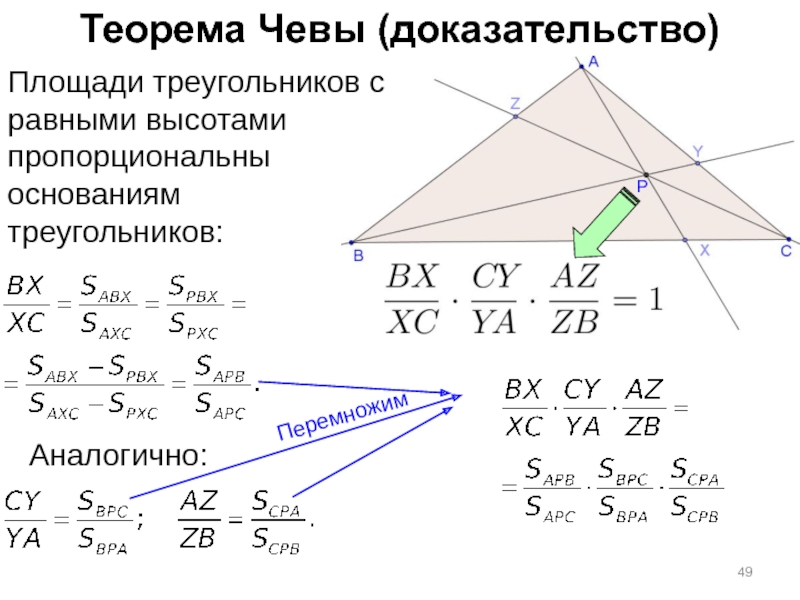
- 44. Теорема Чевы (доказательство) Площади треугольников с равными высотами пропорциональны основаниям треугольников:
- 45. Теорема Чевы (доказательство) Площади треугольников с равными высотами пропорциональны основаниям треугольников:
- 46. Теорема Чевы (доказательство) Площади треугольников с равными высотами пропорциональны основаниям треугольников:
- 47. Теорема Чевы (доказательство) Площади треугольников с равными высотами пропорциональны основаниям треугольников: Аналогично:
- 48. Теорема Чевы (доказательство) Площади треугольников с равными высотами пропорциональны основаниям треугольников: Аналогично: Перемножим
- 49. Теорема Чевы (доказательство) Площади треугольников с равными высотами пропорциональны основаниям треугольников: Аналогично: Перемножим
- 50. Теорема Чевы (доказательство) Площади треугольников с равными высотами пропорциональны основаниям треугольников: Аналогично: Перемножим
- 51. Теорема Чевы (доказательство) P
- 52. Теорема Чевы (доказательство) P Пусть AX
- 53. Теорема Чевы (доказательство) P Пусть AX
- 54. Теорема Чевы (доказательство) P Пусть AX
- 55. Теорема Чевы (доказательство) P Пусть AX
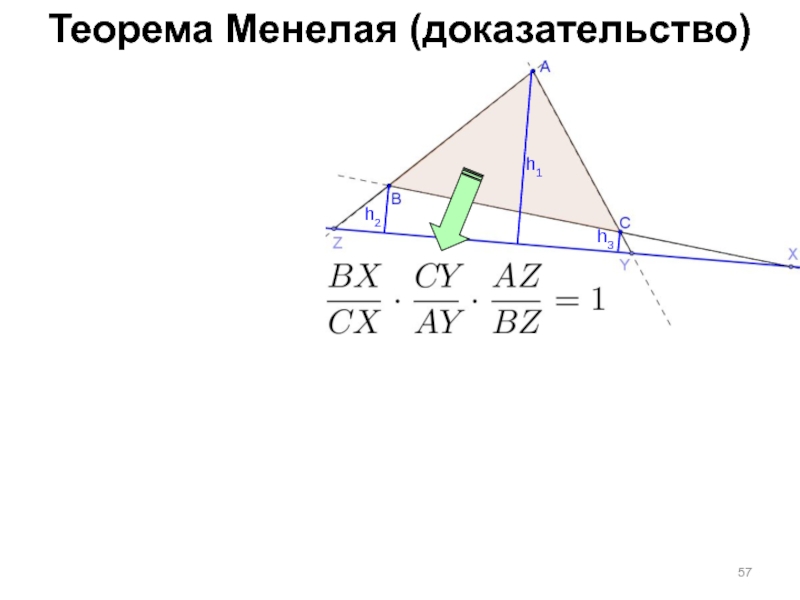
- 56. Теорема Менелая (доказательство)
- 57. Теорема Менелая (доказательство) h1 h3 h2
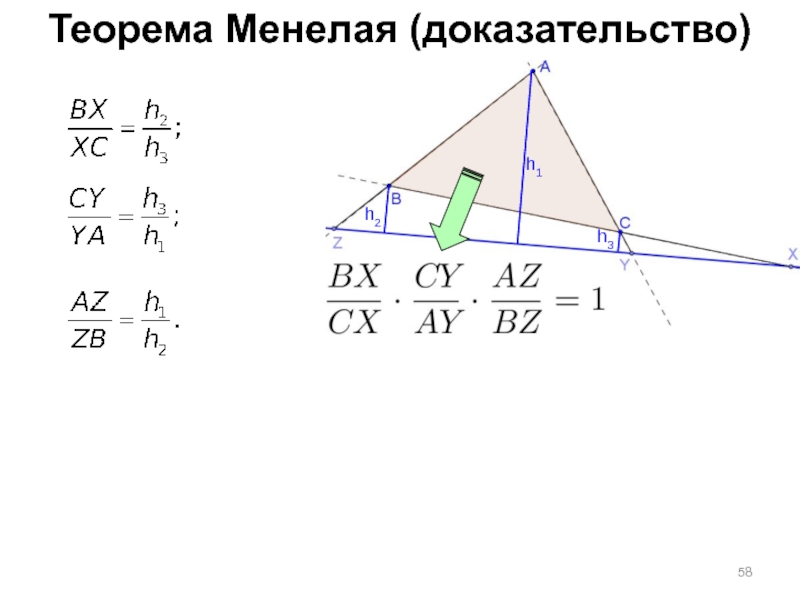
- 58. Теорема Менелая (доказательство) h1 h3 h2
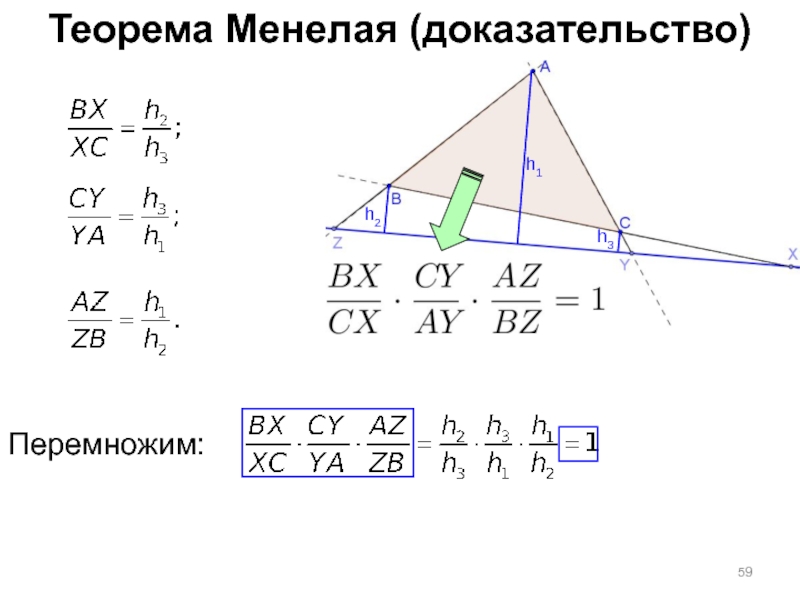
- 59. Теорема Менелая (доказательство) h1 h3 h2 Перемножим:
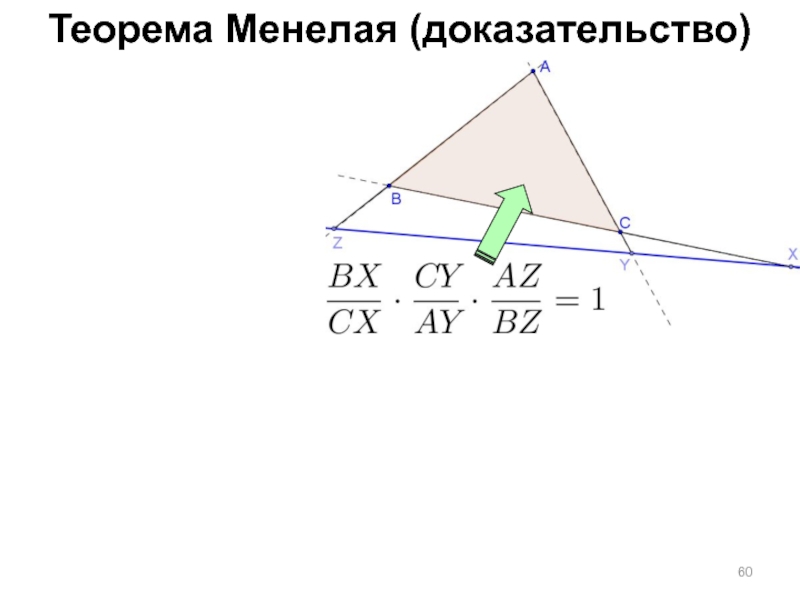
- 60. Теорема Менелая (доказательство)
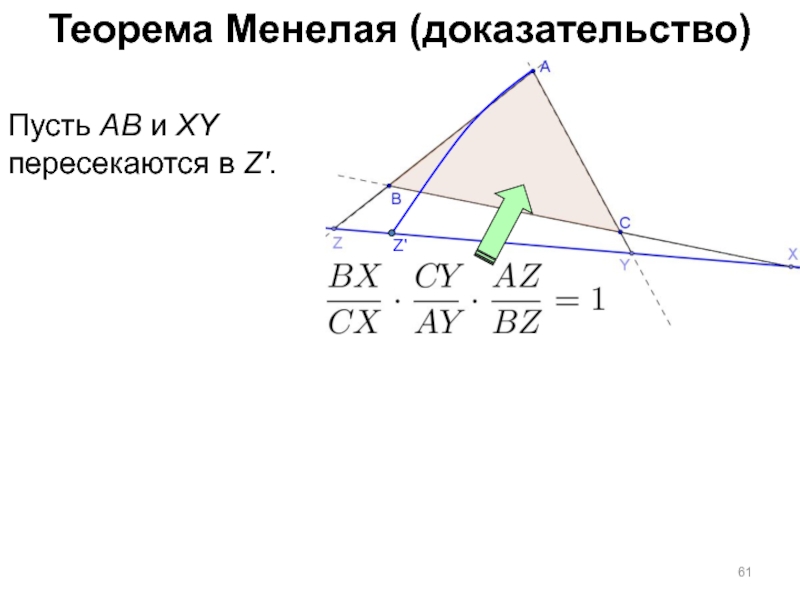
- 61. Теорема Менелая (доказательство) Пусть AB и XY пересекаются в Z'. Z'
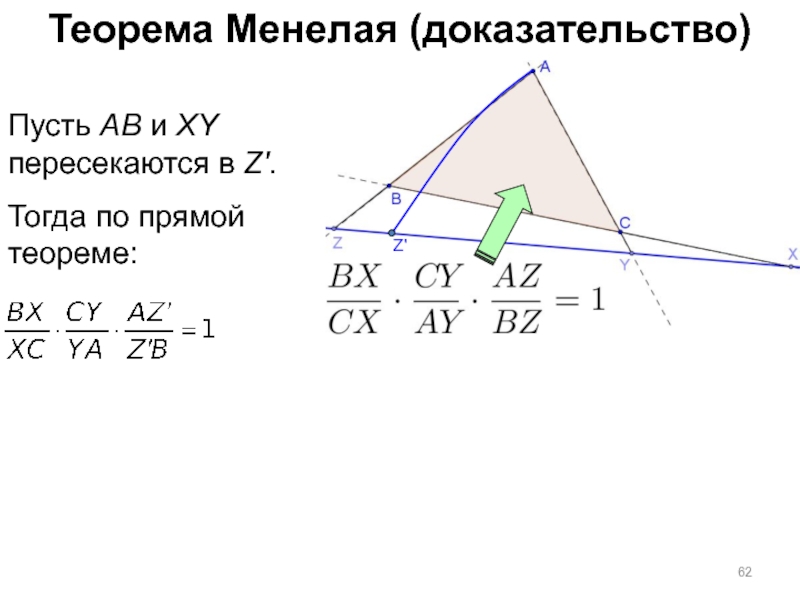
- 62. Теорема Менелая (доказательство) Пусть AB и
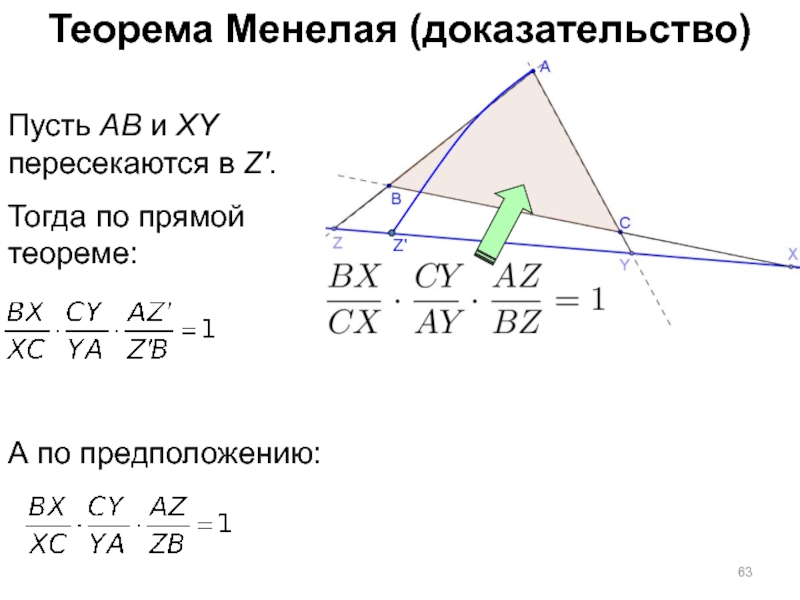
- 63. Теорема Менелая (доказательство) Пусть AB и
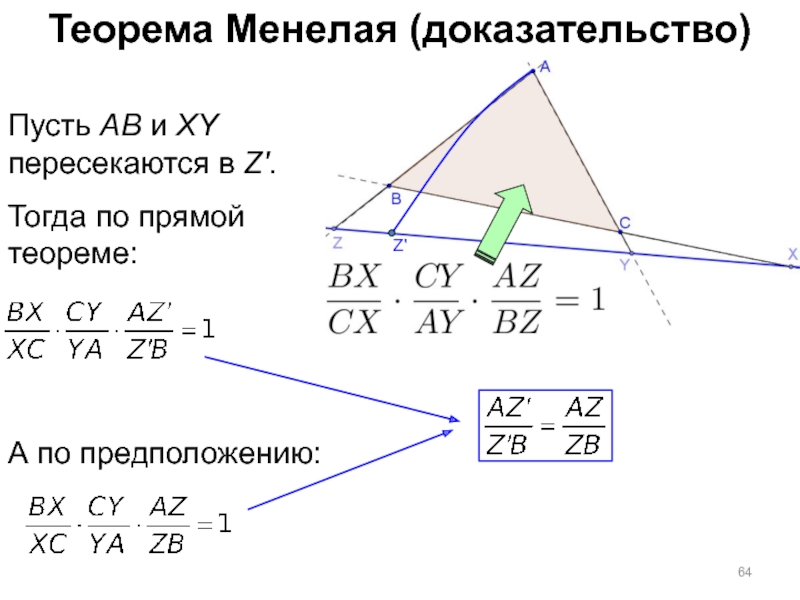
- 64. Теорема Менелая (доказательство) Пусть AB и
1. Некоторые воспоминания
Слайд 9Взаимно-двойственные элементы
точка
прямая
Взаимно-двойственные операции
провести прямую через точку
отметить точку
на прямой
Слайд 15Принцип двойственности
Из каждого проективного предложения относительно точек и прямых на
плоскости может быть получено второе предложение путём замены
слова «точка» словом «прямая»
и наоборот.
Жан Виктор Понселе
офицер инженерного корпуса.
Написано в г.Саратове в 1812-1815 г.г.
Жан Виктор Понселе
офицер инженерного корпуса.
Написано в г.Саратове в 1812-1815 г.г.
Слайд 16Принцип двойственности
Две фигуры взаимно двойственны,
если одна может быть получена из
другой посредством замены
каждого элемента и каждой операции двойственным элементом
и двойственной операцией.
Слайд 17Принцип двойственности
Две теоремы взаимно двойственны,
если одна превращается в другую
при замене
каждого элемента
и каждой операции
двойственным элементом
и двойственной
операцией.
операцией.
Слайд 18Принцип двойственности
Явление двойственности резко отличает проективную геометрию
от элементарной (метрической),
в которой
никакой двойственности не наблюдается.
Слайд 19Принцип двойственности
Явление двойственности резко отличает проективную геометрию
от элементарной (метрической),
в которой
никакой двойственности не наблюдается.
Например, бессмысленно искать какое-нибудь «двойственное» утверждение по отношению к тому факту, что данный угол содержит 37° или что данный отрезок равен 2 линейным единицам.
Например, бессмысленно искать какое-нибудь «двойственное» утверждение по отношению к тому факту, что данный угол содержит 37° или что данный отрезок равен 2 линейным единицам.
Слайд 20Принцип двойственности
Каждой верной теореме
проективной геометрии
сопоставляется двойственная ей,
также верная теорема.
Слайд 21Принцип двойственности
Каждой верной теореме
проективной геометрии
сопоставляется двойственная ей,
также верная теорема.
Следствие. Двойственную
теорему
можно не доказывать.
Слайд 22Перспективность относительно точки
Есть две конфигурации из точек
(могут быть и проходящие
через них прямые).
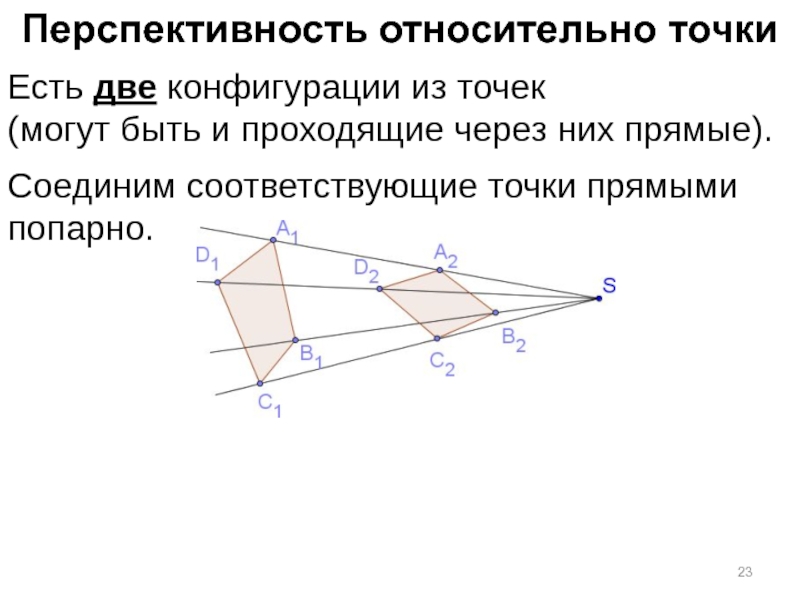
Слайд 23Перспективность относительно точки
Есть две конфигурации из точек
(могут быть и проходящие
через них прямые).
Соединим соответствующие точки прямыми попарно.
Соединим соответствующие точки прямыми попарно.
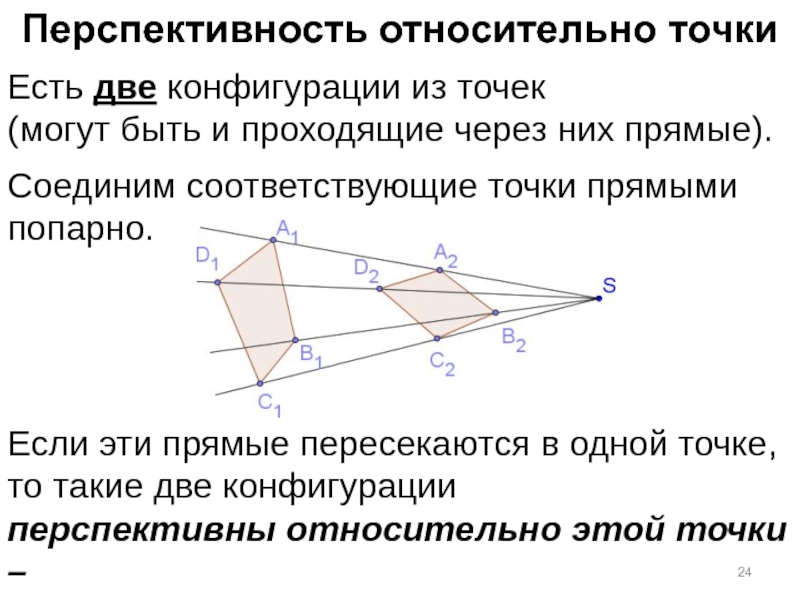
Слайд 24Перспективность относительно точки
Есть две конфигурации из точек
(могут быть и проходящие
через них прямые).
Соединим соответствующие точки прямыми попарно.
Если эти прямые пересекаются в одной точке,
то такие две конфигурации перспективны относительно этой точки – центра перспективы.
Соединим соответствующие точки прямыми попарно.
Если эти прямые пересекаются в одной точке,
то такие две конфигурации перспективны относительно этой точки – центра перспективы.
Слайд 25Перспективность относительно прямой
Есть две конфигурации из прямых
(могут быть выделены точки
их пересечения).
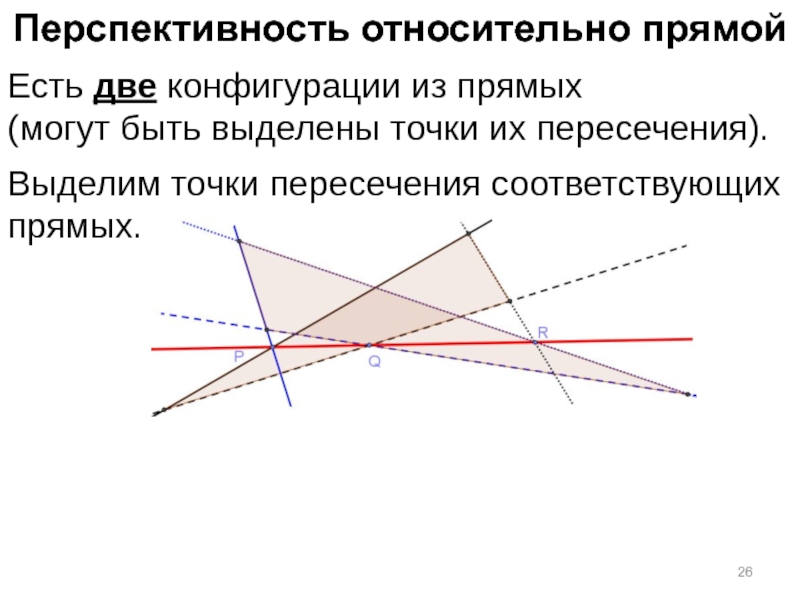
Слайд 26Перспективность относительно прямой
Есть две конфигурации из прямых
(могут быть выделены точки
их пересечения).
Выделим точки пересечения соответствующих прямых.
Выделим точки пересечения соответствующих прямых.
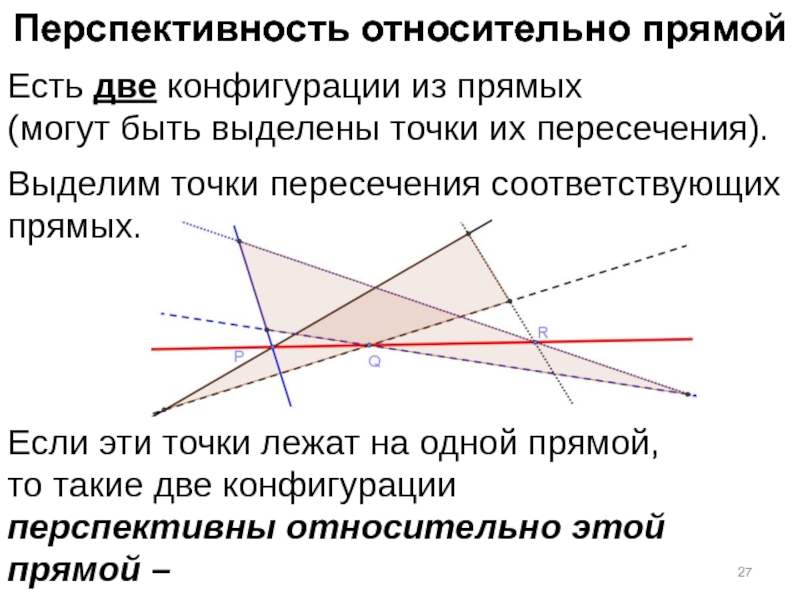
Слайд 27Перспективность относительно прямой
Есть две конфигурации из прямых
(могут быть выделены точки
их пересечения).
Выделим точки пересечения соответствующих прямых.
Если эти точки лежат на одной прямой,
то такие две конфигурации перспективны относительно этой прямой – оси перспективы.
Выделим точки пересечения соответствующих прямых.
Если эти точки лежат на одной прямой,
то такие две конфигурации перспективны относительно этой прямой – оси перспективы.
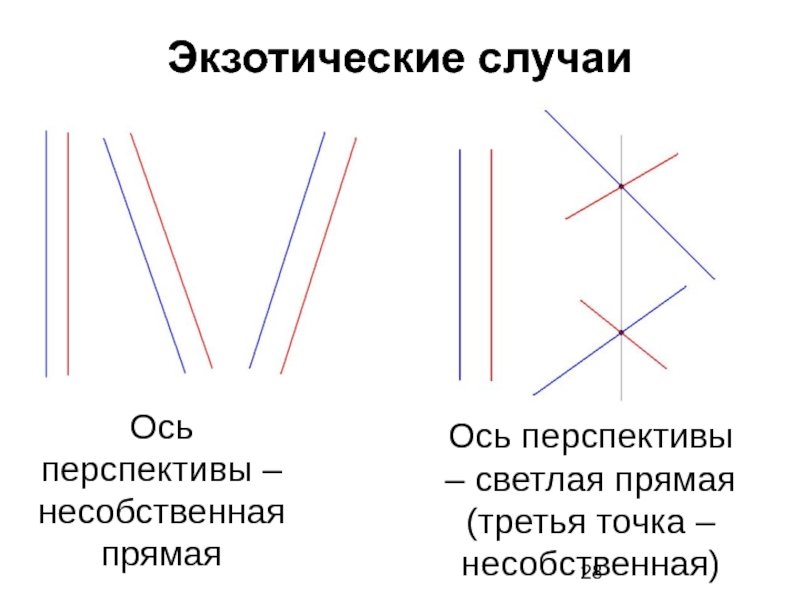
Слайд 28Экзотические случаи
Ось перспективы – несобственная прямая
Ось перспективы – светлая прямая (третья
точка – несобственная)
Слайд 36Теорема Чевы
Если три чевианы AX, BY, CZ треугольника ABC конкуррентны,
то выполняется
соотношение (*).
(*)
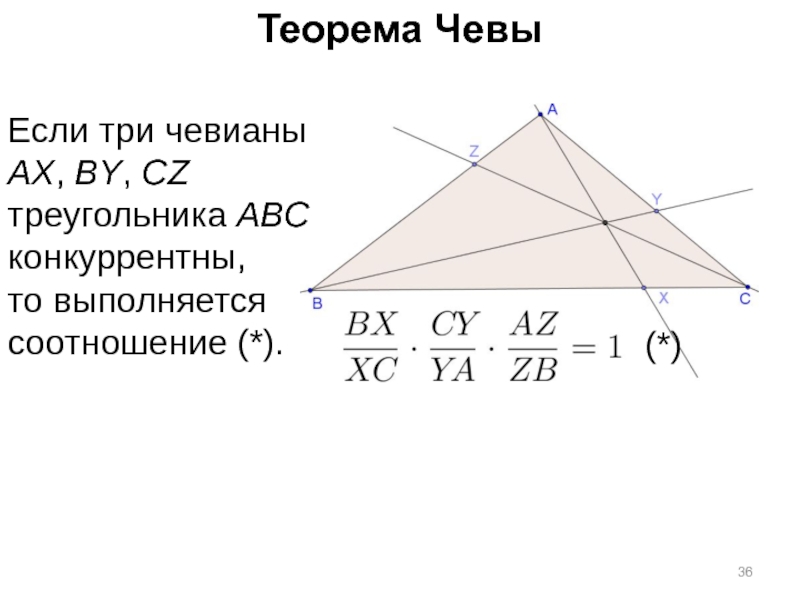
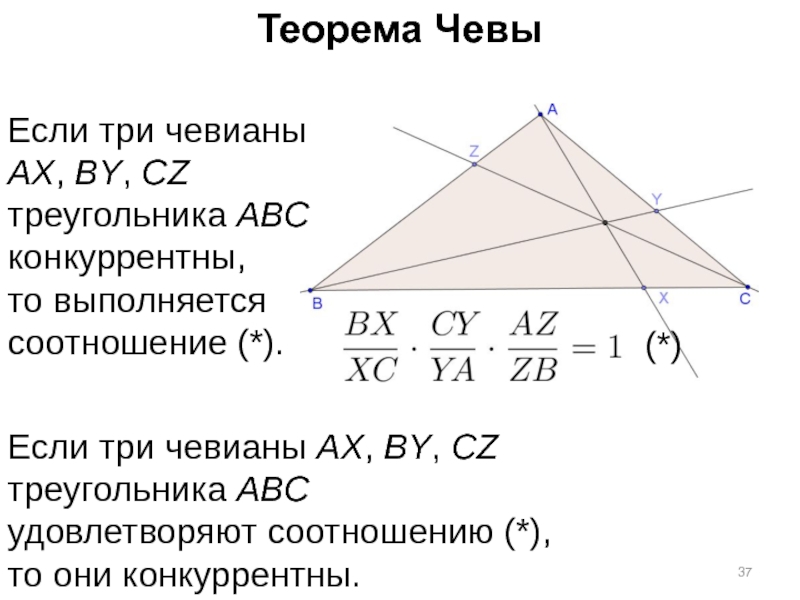
Слайд 37Теорема Чевы
Если три чевианы AX, BY, CZ треугольника ABC конкуррентны,
то выполняется
соотношение (*).
Если три чевианы AX, BY, CZ
треугольника ABC
удовлетворяют соотношению (*), то они конкуррентны.
(*)
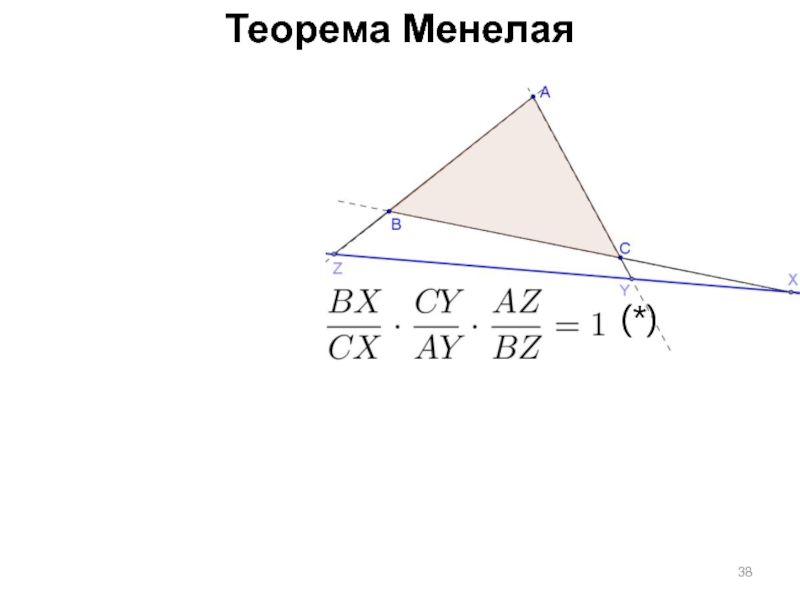
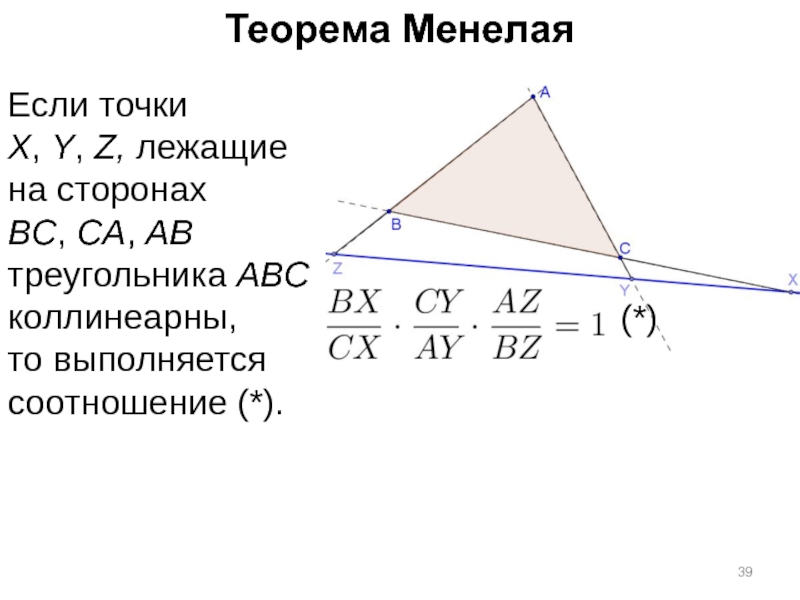
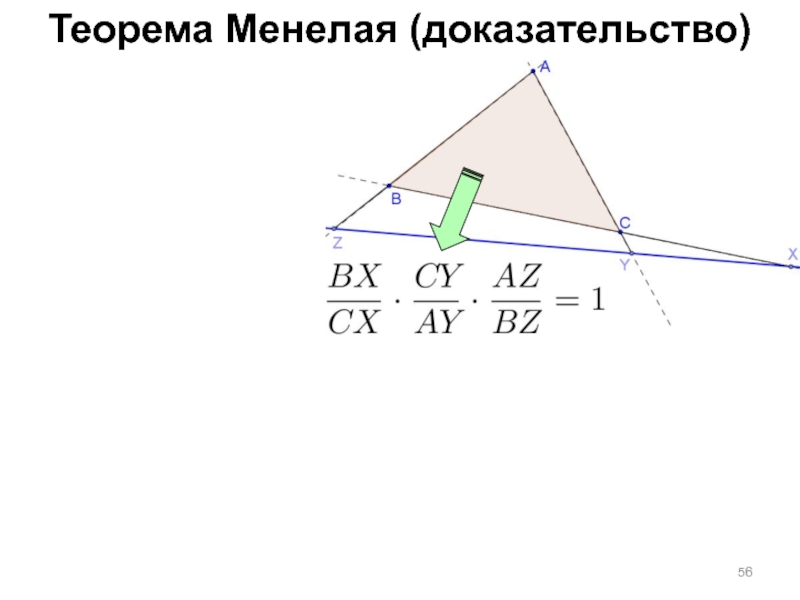
Слайд 39Теорема Менелая
Если точки
X, Y, Z, лежащие на сторонах
BC, CA, AB треугольника
ABC коллинеарны,
то выполняется соотношение (*).
(*)
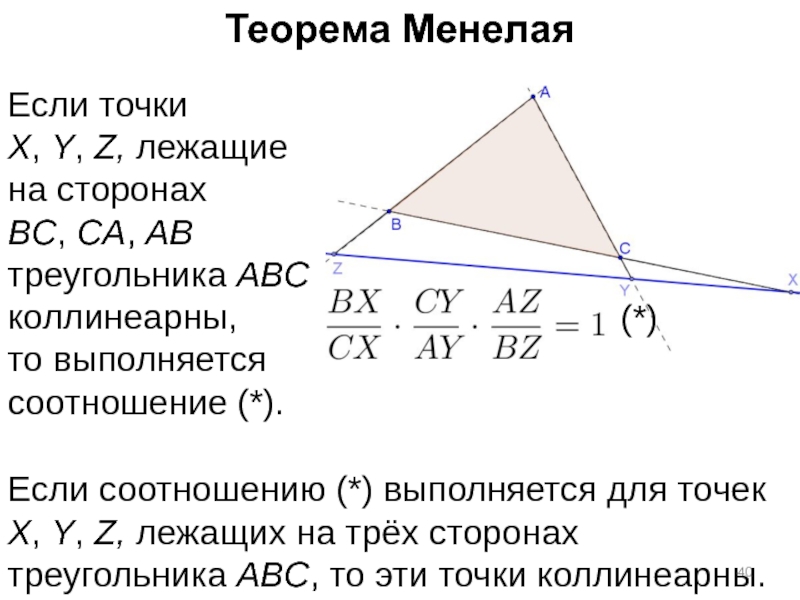
Слайд 40Теорема Менелая
Если точки
X, Y, Z, лежащие на сторонах
BC, CA, AB треугольника
ABC коллинеарны,
то выполняется соотношение (*).
Если соотношению (*) выполняется для точек X, Y, Z, лежащих на трёх сторонах треугольника ABC, то эти точки коллинеарны.
(*)
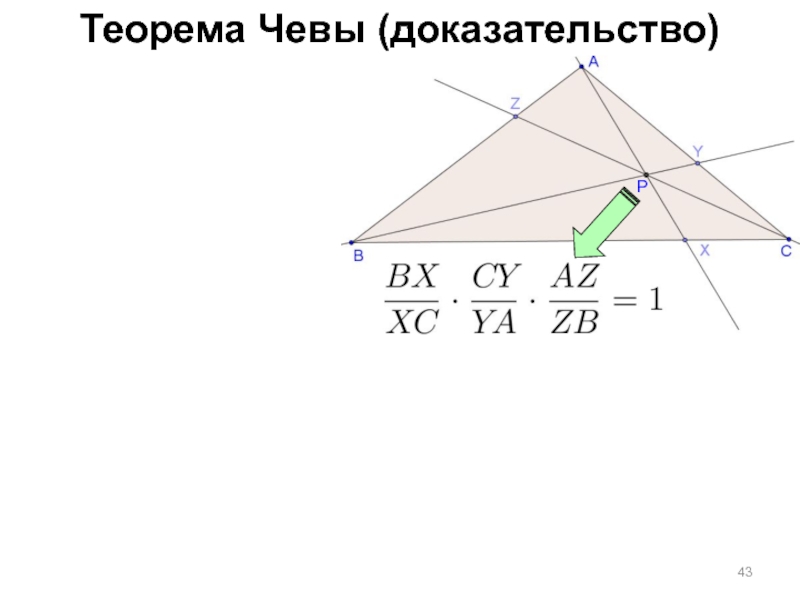
Слайд 44Теорема Чевы (доказательство)
Площади треугольников с равными высотами пропорциональны основаниям
треугольников:
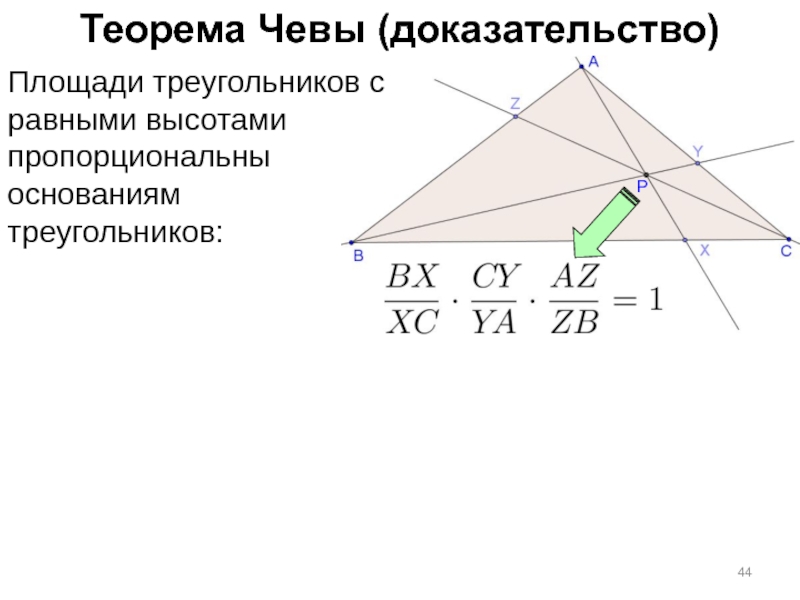
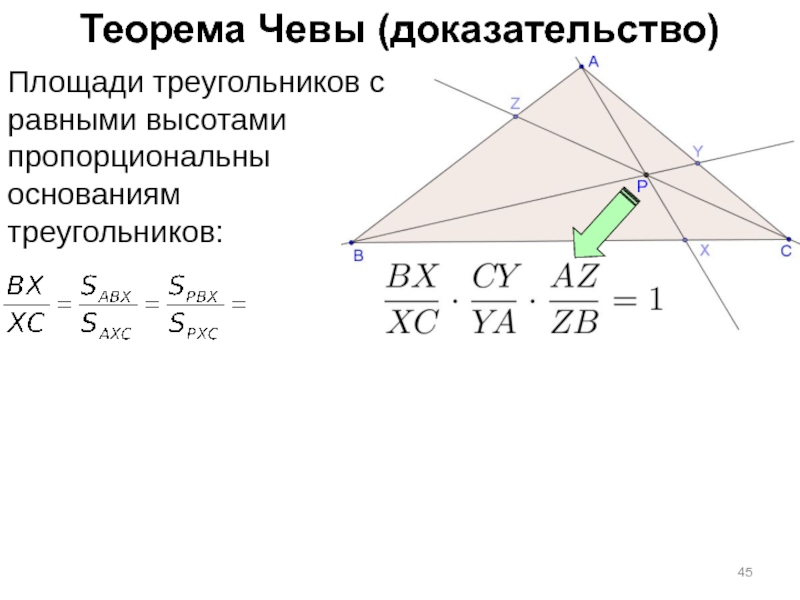
Слайд 45Теорема Чевы (доказательство)
Площади треугольников с равными высотами пропорциональны основаниям
треугольников:
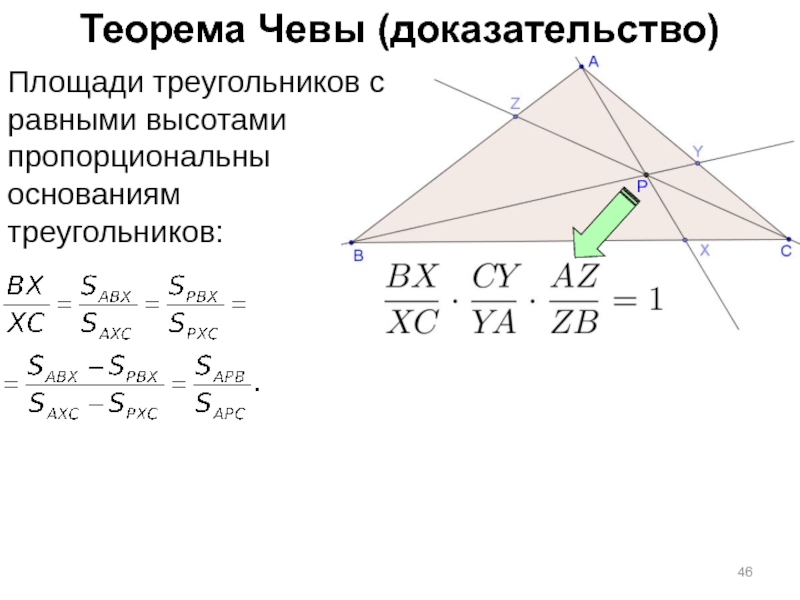
Слайд 46Теорема Чевы (доказательство)
Площади треугольников с равными высотами пропорциональны основаниям
треугольников:
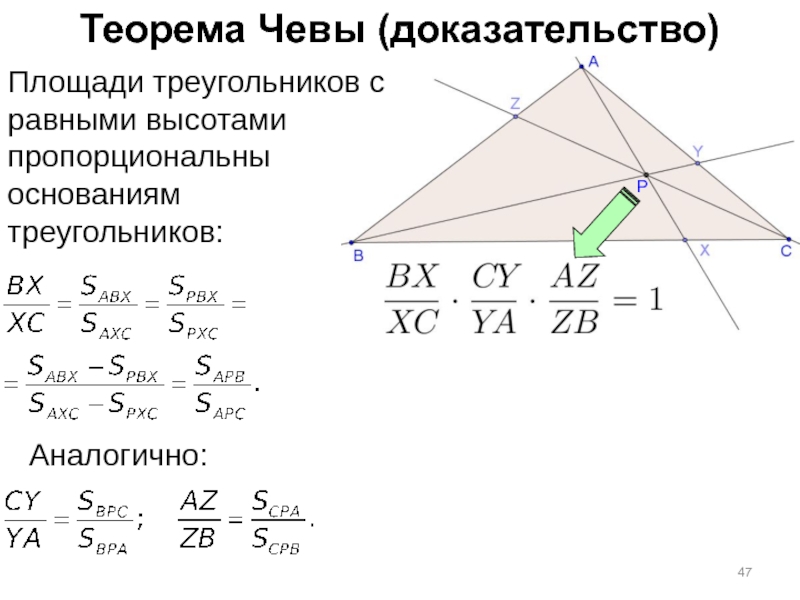
Слайд 47Теорема Чевы (доказательство)
Площади треугольников с равными высотами пропорциональны основаниям
треугольников:
Аналогично:
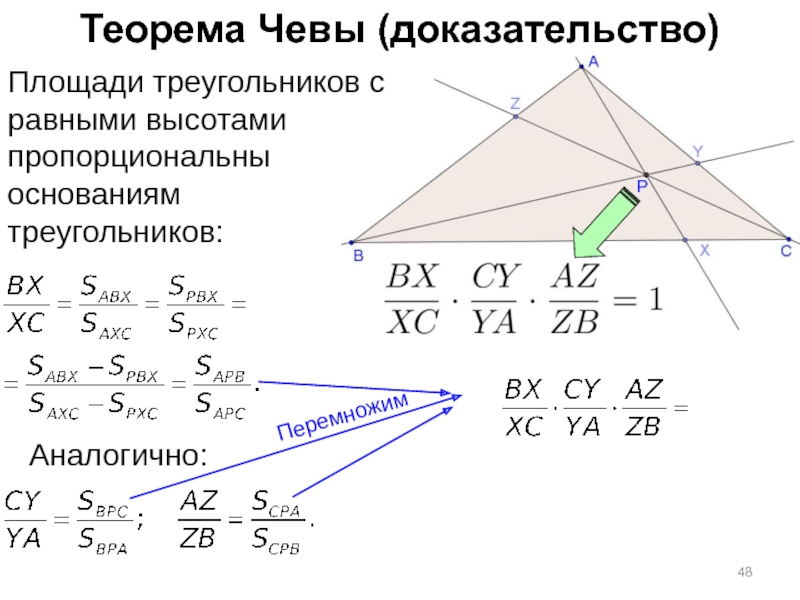
Слайд 48Теорема Чевы (доказательство)
Площади треугольников с равными высотами пропорциональны основаниям
треугольников:
Аналогично:
Перемножим
Слайд 49Теорема Чевы (доказательство)
Площади треугольников с равными высотами пропорциональны основаниям
треугольников:
Аналогично:
Перемножим
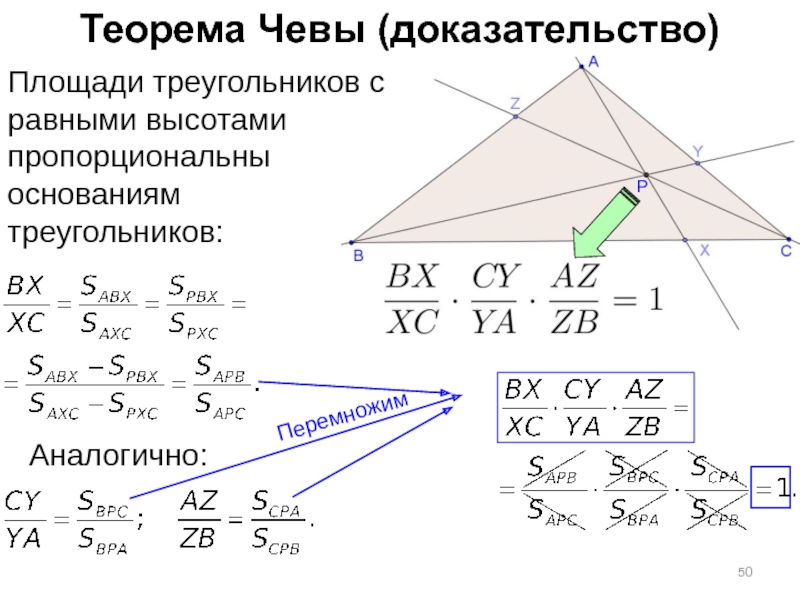
Слайд 50Теорема Чевы (доказательство)
Площади треугольников с равными высотами пропорциональны основаниям
треугольников:
Аналогично:
Перемножим
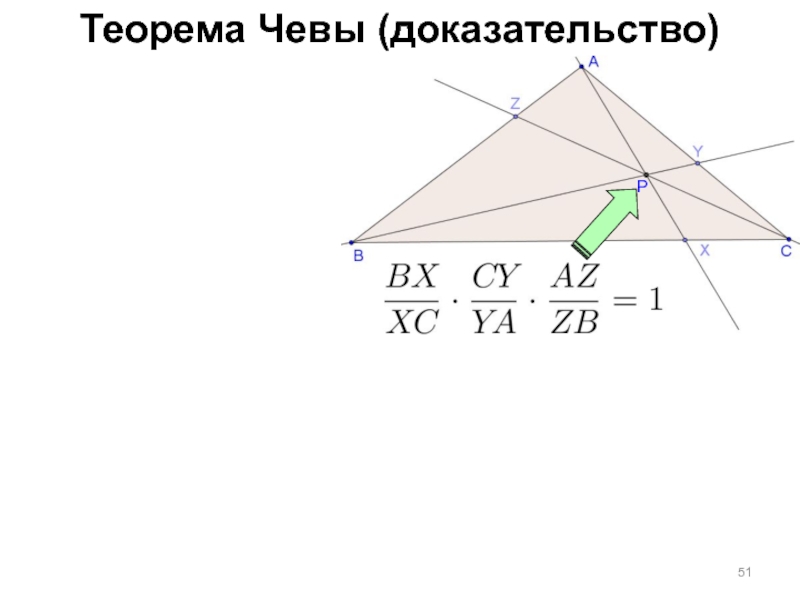
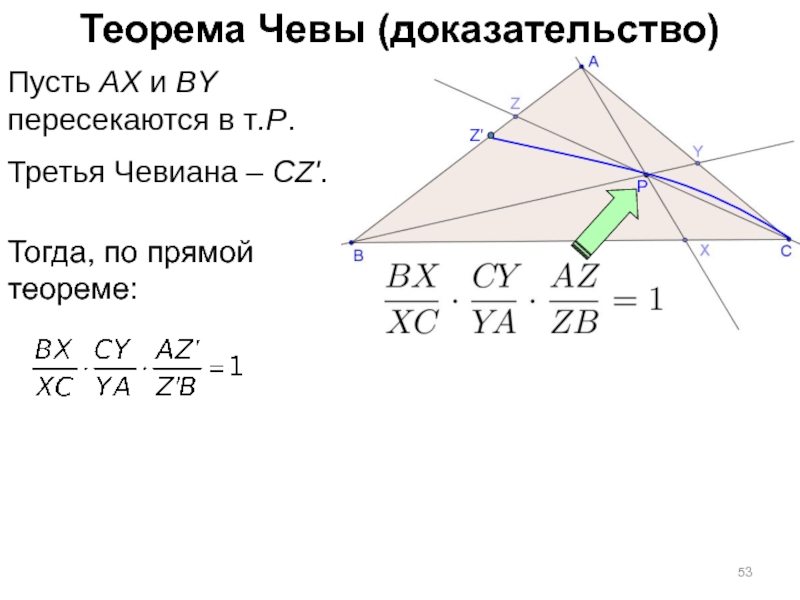
Слайд 53Теорема Чевы (доказательство)
P
Пусть AX и BY
пересекаются в т.P.
Третья Чевиана –
CZ'.
Z'
Тогда, по прямой
теореме:
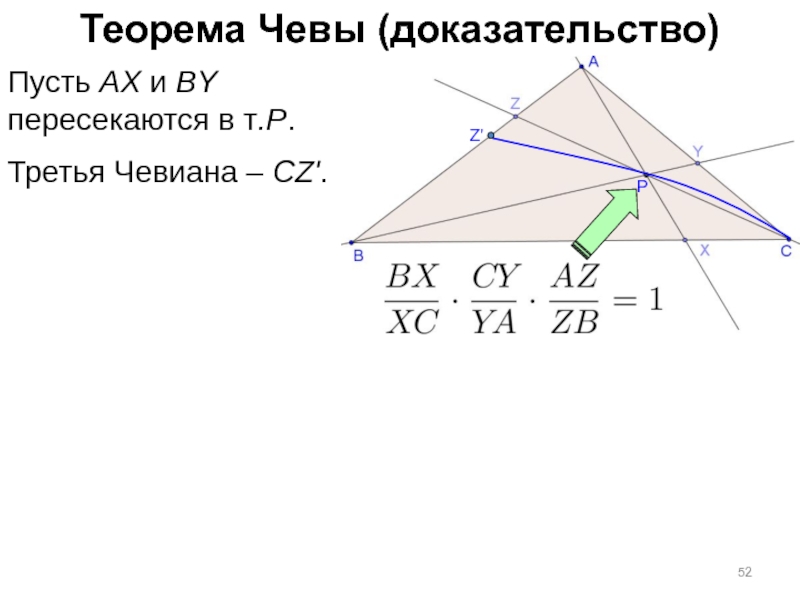
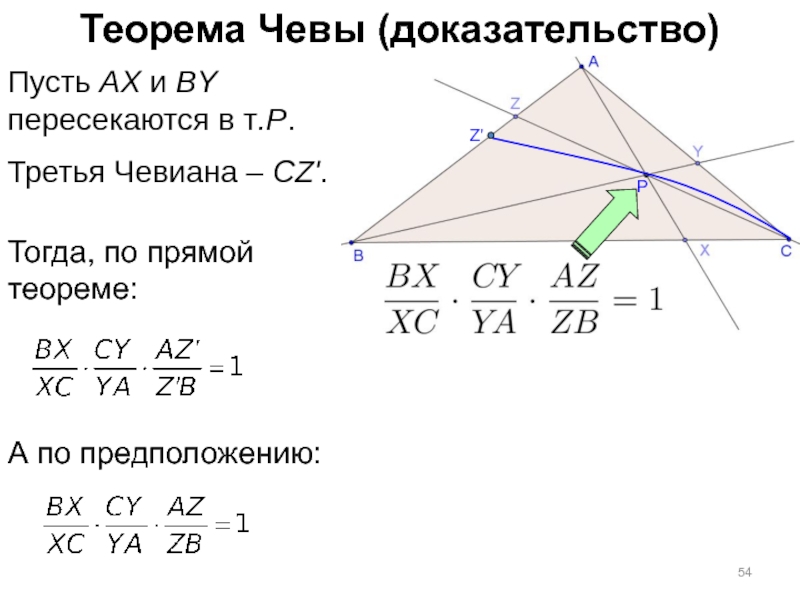
Слайд 54Теорема Чевы (доказательство)
P
Пусть AX и BY
пересекаются в т.P.
Третья Чевиана –
CZ'.
Z'
Тогда, по прямой
теореме:
А по предположению:
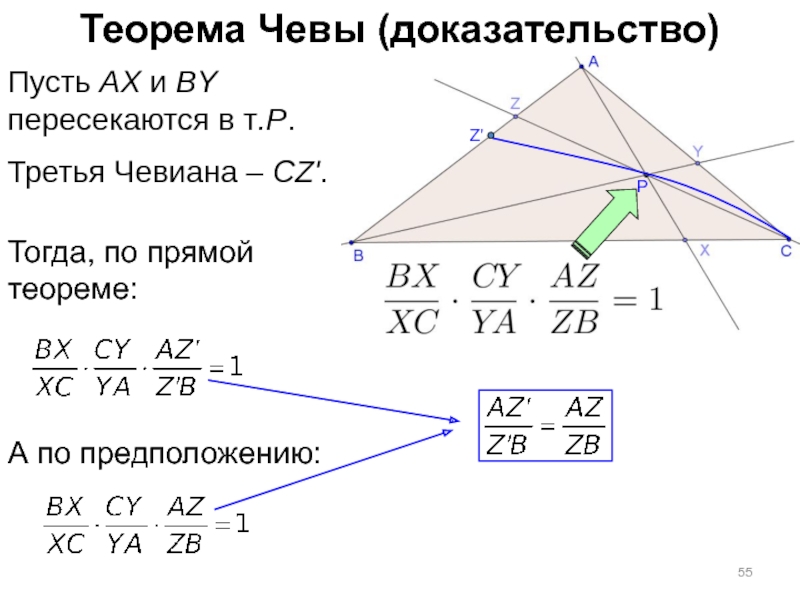
Слайд 55Теорема Чевы (доказательство)
P
Пусть AX и BY
пересекаются в т.P.
Третья Чевиана –
CZ'.
Z'
Тогда, по прямой
теореме:
А по предположению:
Слайд 63Теорема Менелая (доказательство)
Пусть AB и XY пересекаются в Z'.
Тогда по прямой
теореме:
А
по предположению:
Z'
Слайд 64Теорема Менелая (доказательство)
Пусть AB и XY пересекаются в Z'.
Тогда по прямой
теореме:
А
по предположению:
Z'
