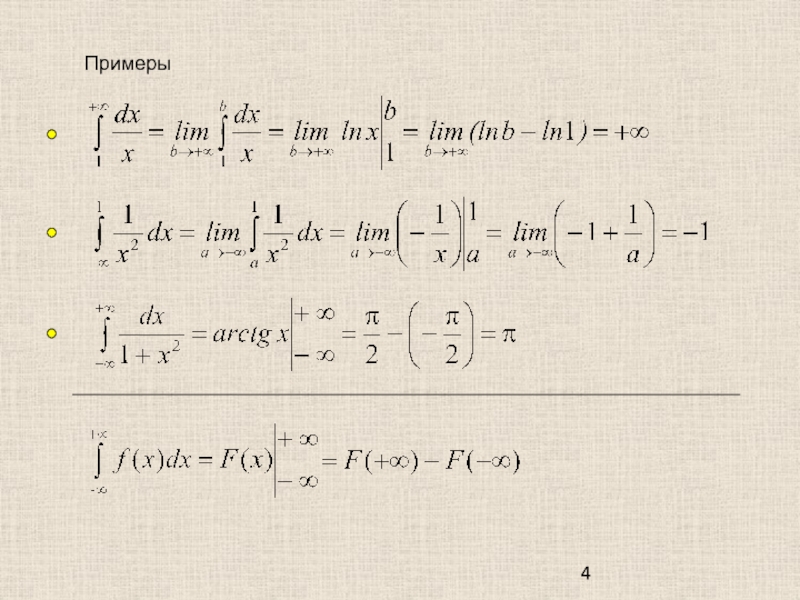- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Несобственные интегралы (лекция 7) презентация
Содержание
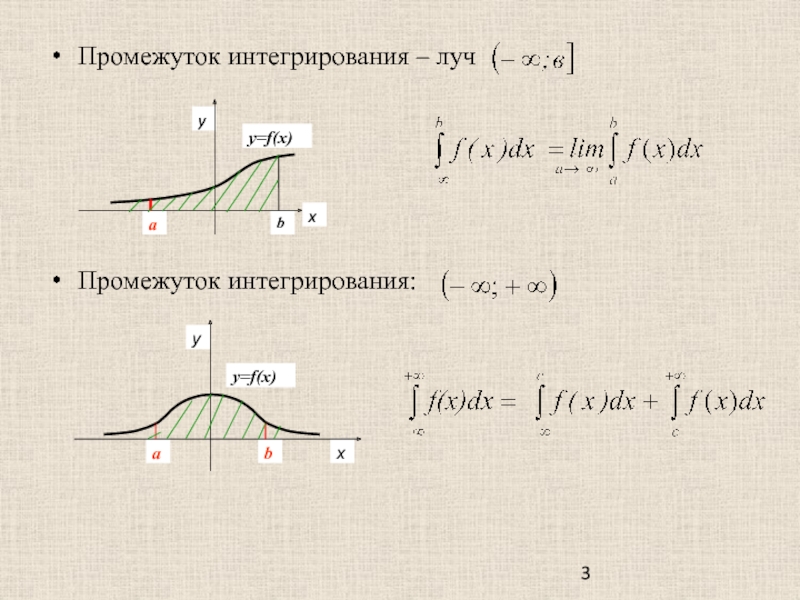
Слайд 2Несобственные интегралы с бесконечными пределами интегрирования ( I рода)
Пусть промежутком интегрирования
является луч , а функция y=f(x) интегрируема на каждом конечном отрезке [a,b].
Геометрически задача состоит в нахождении площади под кривой.
Возьмем точку в, найдем площадь криволинейной трапеции через определенный интеграл и устремим в к .
Геометрически задача состоит в нахождении площади под кривой.
Возьмем точку в, найдем площадь криволинейной трапеции через определенный интеграл и устремим в к .
в
x
y
y=f(x)
а
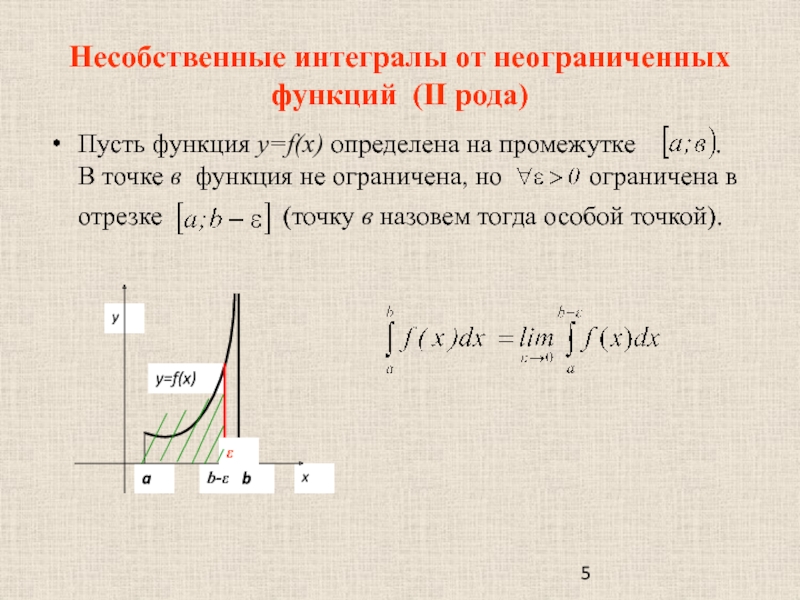
Слайд 5Несобственные интегралы от неограниченных функций (II рода)
Пусть функция y=f(x) определена на
промежутке . В точке в функция не ограничена, но ограничена в отрезке (точку в назовем тогда особой точкой).
b-ε
y
x
b
a
y=f(x)
ε
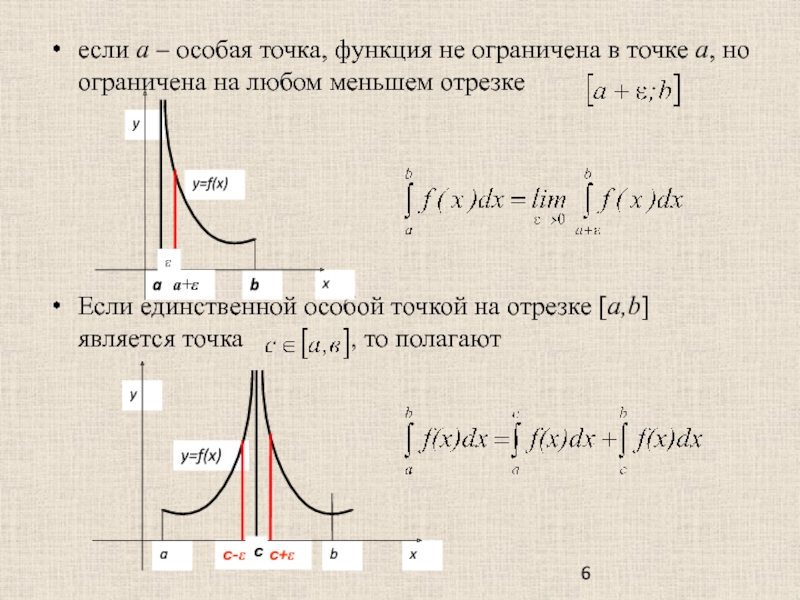
Слайд 6если а – особая точка, функция не ограничена в точке а,
но ограничена на любом меньшем отрезке
Если единственной особой точкой на отрезке [a,b] является точка , то полагают
Если единственной особой точкой на отрезке [a,b] является точка , то полагают
x
y
b
a
y=f(x)
ε
a+ε
x
с+ε
с-ε
y
b
a
y=f(x)
с