- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЛА-УП-Л3 презентация
Содержание
- 1. ЛА-УП-Л3
- 2. План лекции Система линейных алгебраических уравнений Совместность,
- 3. Системы линейных уравнений (СЛУ) Под
- 4. Матричная запись СЛУ A
- 5. Решение СЛУ Решением СЛУ
- 6. Матричная запись решения СЛУ
- 7. Типы СЛУ СЛУ называется совместной, если у
- 8. Расширенная матрица СЛУ Вся информация о СЛУ
- 9. по
- 10. Пусть дана совместная СЛУ от n неизвестных
- 11. Найти решение СЛУ
- 12. Пусть дана совместная СЛАУ от n неизвестных
- 13. Метод Гаусса решения СЛУ Суть метода состоит
- 14. Пример (тот же): или Метод Гаусса решения СЛАУ. Пример
- 15. Алгоритм решения произвольной СЛУ полагая
- 16. В результате преобразований система примет вид
- 17. б) полагая
- 18. 2. Укороченная система 2. Отбросив
- 19. 3. Назовем неизвестные x1, x2,…,xr базисными,
- 20. 4. Для каждого набора свободных неизвестных
- 21. Найти общее решение СЛУ Положим x3=c1, x2=c2
- 22. Теорема о числе решений СЛУ
- 23. Следствия из теоремы о числе решений
- 24. Общее решение однородной системы имеет вид
- 25. Найти фундаментальное множество решений СЛУ Фундаментальное множество
- 26. Общее решение системы может быть записано так:
- 27. Общее решение неоднородной системы A.X =
- 28. Найти множество решений СЛУ n-r = 2
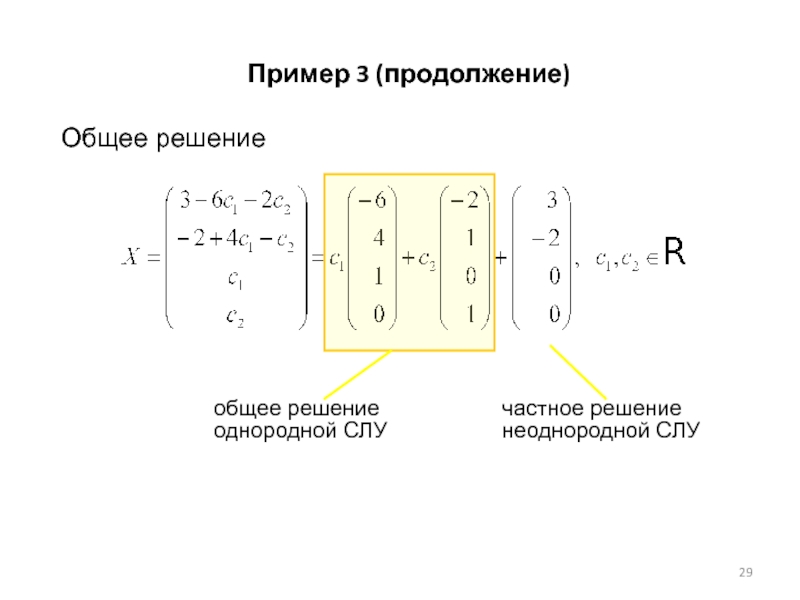
- 29. Пример 3 (продолжение) Общее решение
Слайд 2План лекции
Система линейных алгебраических уравнений
Совместность, определенность и равносильность систем
Методы решения систем:
Метод
Метод обратной матрицы;
Метод Гаусса.
Количество решений системы
Случай однородных систем
Слайд 3 Системы линейных уравнений (СЛУ)
Под системой линейных уравнений (СЛУ) будем
где – «неизвестные» системы,
– коэффициенты системы,
m – число уравнений, n – число неизвестных.
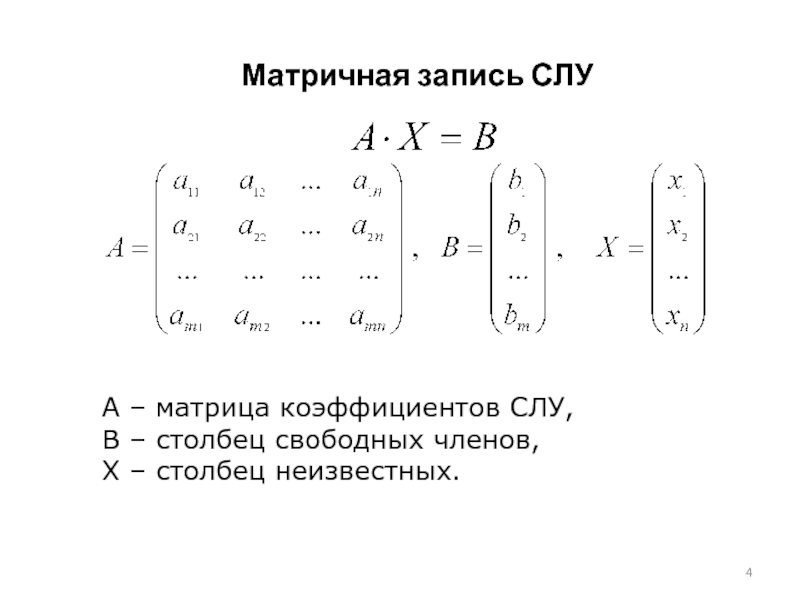
Слайд 4 Матричная запись СЛУ
A – матрица коэффициентов СЛУ,
B
X – столбец неизвестных.
Слайд 5 Решение СЛУ
Решением СЛУ называется совокупность чисел
,
удовлетворяющая всем уравнениям системы, т.е. обращающая их в верные числовые равенства:
Слайд 7 Типы СЛУ
СЛУ называется совместной, если у неё имеется хотя бы одно
Совместная СЛУ называется определённой, если она имеет одно единственное решение и неопределённой в противном случае.
Две системы называются равносильными, если их множества решений совпадают.
СЛАУ A.X=B называется однородной, если B=0 , в противном случае СЛУ называется неоднородной.
Слайд 9
по правилу Крамера,
методом обратной матрицы,
методом Гаусса.
Пусть дана совместная определенная СЛАУ
Тогда:
если система однородна, то она имеет только тривиальное решение xi = 0, i=1,…,n;
если система не однородна, то она имеет единственное решение, которое может быть найдено
Совместная СЛУ
Слайд 10 Пусть дана совместная СЛУ от n неизвестных
Тогда система имеет единственное решение
где
Правило Крамера решения СЛУ
Слайд 12Пусть дана совместная СЛАУ от n неизвестных
Тогда существует A-1 и
Пример (тот же).
Метод обратной матрицы решения СЛУ
Слайд 13 Метод Гаусса решения СЛУ
Суть метода состоит в последовательном исключении неизвестных: сначала
Слайд 15 Алгоритм решения произвольной СЛУ
полагая
к 2-му уравнению прибавим 1-ое, умноженное на ,
к 3-му уравнению прибавим 1-ое, умноженное на ,
. . . . . . . . . ,
к n-ому уравнению прибавим 1-ое, умноженное на .
1. Приведем СЛУ к системе с матрицей A1 трапециевидного (ступенчатого) вида:
Слайд 17
б) полагая ,
. . . . . . . . . ,
к n-ому уравнению прибавим 2-ое, умноженное на .
в) и т.д.
Слайд 18 2. Укороченная система
2. Отбросив последние n – r уравнений,
Слайд 193. Назовем неизвестные x1, x2,…,xr базисными, xr+1, xr+2,…,xn – свободными.
Запишем
3. Свободные и базисные неизвестные
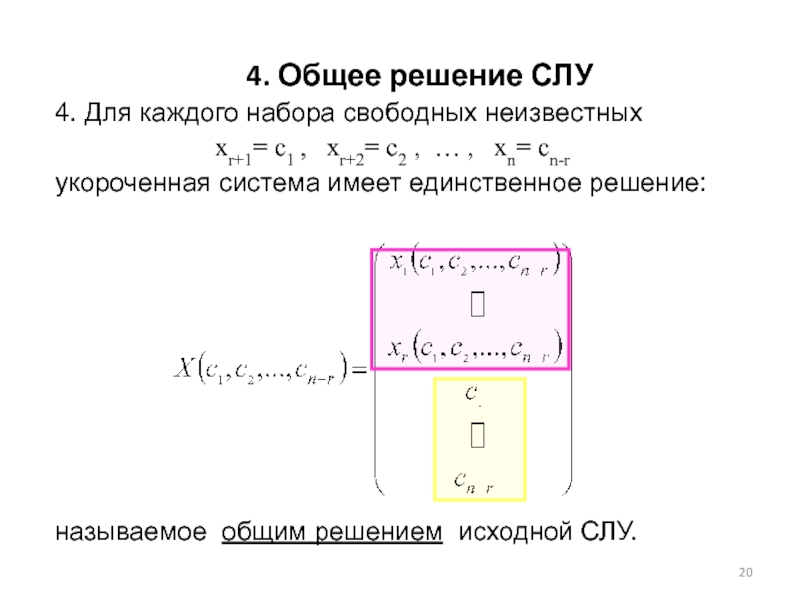
Слайд 204. Для каждого набора свободных неизвестных
xr+1= с1 , xr+2=
укороченная система имеет единственное решение:
называемое общим решением исходной СЛУ.
4. Общее решение СЛУ
Слайд 21Найти общее решение СЛУ
Положим x3=c1, x2=c2 .
Укороченная система имеет вид
Общее решение .
Общее решение СЛУ. Пример 2
Слайд 22 Теорема о числе решений СЛУ
Пусть дана совместная СЛУ от
Тогда:
1. если r = n , то система имеет единственное решение;
2. если r < n , то система имеет бесконечно много решений, причем (n – r) неизвестным можно присвоить произвольные значения, а остальные r неизвестных выражаются через них единственным образом.
Слайд 23 Следствия из теоремы о числе решений СЛУ
Система n линейных уравнений
Однородная система A.X= 0 всегда совместна, т.к. имеет тривиальное решение X= 0. Для существования нетривиального решения однородной системы необходимо и достаточно, чтобы выполнялось r < n.
Слайд 24Общее решение однородной системы имеет вид
где с1, с2,…,сn-r – произвольные
Фундаментальное множество решений
может быть получено из общего решения, если свободным неизвестным придавать поочередно значение 1, полагая остальные равными 0.
Фундаментальное множество решений
однородной СЛУ
Слайд 25Найти фундаментальное множество решений СЛУ
Фундаментальное множество решений
однородной СЛУ. Пример 2
Общее решение
При c1=1, c2=0 , при c2=1, c1=0 .
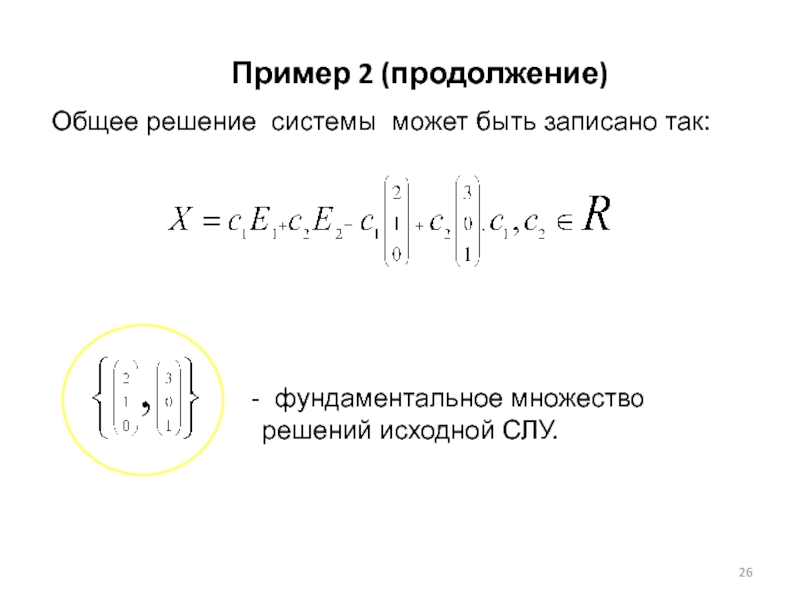
Слайд 26Общее решение системы может быть записано так:
- фундаментальное множество
Пример 2 (продолжение)
Слайд 27Общее решение неоднородной системы A.X = B может быть
и произвольного частного решения неоднородной системы.
Структура общего решения неоднородной СЛУ
Слайд 28Найти множество решений СЛУ
n-r = 2 . Полагаем x3 = c1
Структура множества решений неоднородной СЛУ. Пример 3
Укороченная система имеет вид