- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кубические уравнения презентация
Содержание
- 1. Кубические уравнения
- 2. Понятие кубического уравнения Кубическое
- 3. Для нахождения корней кубического многочлена существует несколько
- 4. 1. Решение кубических уравнений с помощью вынесения
- 5. 1. 2. 3. 4.
- 6. 2. Решение кубических уравнений с помощью деления
- 7. 1. 2. 3.
- 8. 3. Теорема Виета Алгоритм решения:
- 10. 4. Схема Горнера Алгоритм решения: 1.
- 13. 5. Решение возвратных кубических уравнений Алгоритм
- 15. 6. Графический способ Алгоритм решения: 1.
- 17. Заключение Просмотрев множество способов решения кубических
Слайд 2
Понятие кубического
уравнения
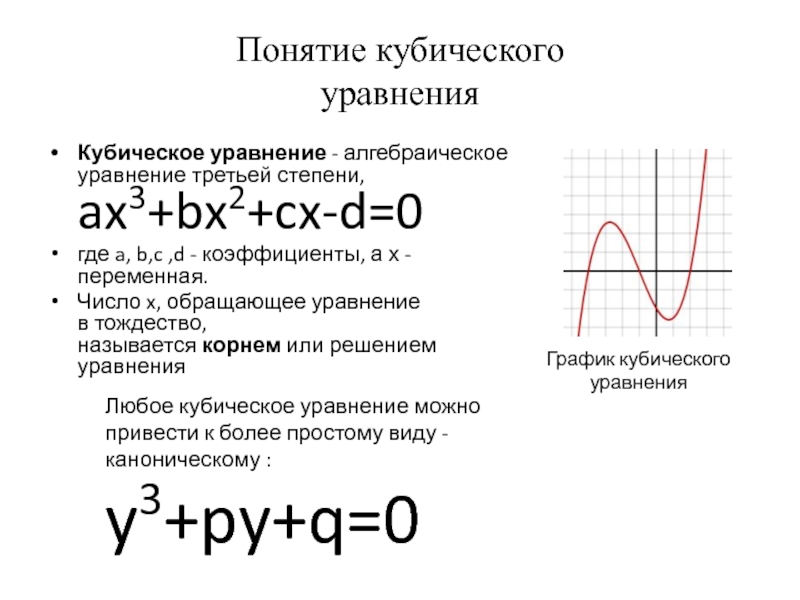
Кубическое уравнение - алгебраическое уравнение третьей степени, ax3+bx2+cx-d=0
где
Число x, обращающее уравнение в тождество, называется корнем или решением уравнения
График кубического уравнения
Любое кубическое уравнение можно привести к более простому виду -каноническому :
y3+py+q=0
Слайд 3Для нахождения корней кубического многочлена существует несколько способов:
1. С помощью вынесения
2. С помощью деления на многочлен;
3. С помощью теоремы Виета;
4. С помощью схемы Горнера;
5. Решение возвратных уравнений;
6. Графический способ.
Слайд 41. Решение кубических уравнений с помощью вынесения общего множителя за скобки
Алгоритм решения:
1. Перегруппировать члены данного уравнения
2. Вынести общий множитель за скобки
3. Получить произведение равное нулю
4. Решить полученные уравнения.
Слайд 62. Решение кубических уравнений с помощью деления многочлен на многочлен
Алгоритм решения:
1.
2. Поделить многочлен на многочлен
3.Найти корни в получившемся квадратном уравнении
Слайд 83. Теорема Виета
Алгоритм решения:
Подобрать корни, удовлетворяющие системе
ax3 + bx2 + cx
x1+x2+x3=-b/a
x1x2+x2x3+x3x1=c/a
x1x2x3=-d/a
,где x1, x2, x3 – корни уравнения
Слайд 104. Схема Горнера
Алгоритм решения:
1. По схеме Горнера найти корень уравнения
2.
Слайд 135. Решение возвратных кубических уравнений
Алгоритм решения:
1. Корнем уравнения является x=-1
2.
3. Найти корни в получившемся
квадратном уравнении
Слайд 156. Графический способ
Алгоритм решения:
1. Разбить кубическое уравнение на два уравнения
2.
3. Абсциссы точек пересечения графиков – корни заданного уравнения
Слайд 17Заключение
Просмотрев множество способов решения кубических уравнений, я остался верен двум
Теперь, выбирая между ними, мне стоит лишь посмотреть на сложность коэффициента уравнения.
Просмотрев множество способов решения кубических уравнений, я остался верен двум на мой взгляд самым надёжным и практичным способам - это теорема Виета и схема Горнера, они позволяют быть уверенным в своем ответе.
Теперь, выбирая между ними, мне стоит лишь посмотреть на сложность коэффициента уравнения.
Просмотрев множество способов решения кубических уравнений, я остался верен двум на мой взгляд самым надёжным и практичным способам - это теорема Виета и схема Горнера, они позволяют быть уверенным в своем ответе.
Теперь, выбирая между ними, мне стоит лишь посмотреть на сложность коэффициента уравнения.