кафедры РК-1 Сенченкова Л.С., Палий Н.В.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кривые линии. Образование и задание поверхностей. (Лекция 3) презентация
Содержание
- 1. Кривые линии. Образование и задание поверхностей. (Лекция 3)
- 2. 6. Кривые линии 1, 2, 3 –
- 3. Плоские кривые Проекции окружности (рис. 25)
- 4. Плоские кривые Проекции окружности (рис. 25)
- 5. Плоские кривые Проекции окружности (рис. 25)
- 6. Плоские кривые Проекции окружности (рис. 25)
- 7. Плоские кривые Проекции окружности (рис. 25)
- 8. Плоские кривые Проекции окружности (рис. 25)
- 9. Плоские кривые Проекции окружности (рис. 25)
- 10. Плоские кривые Проекции окружности (рис. 25)
- 11. Плоские кривые Проекции окружности (рис. 25)
- 12. Плоские кривые Проекции окружности (рис. 25)
- 13. Плоские кривые Проекции окружности (рис. 25)
- 14. Плоские кривые Проекции окружности (рис. 25)
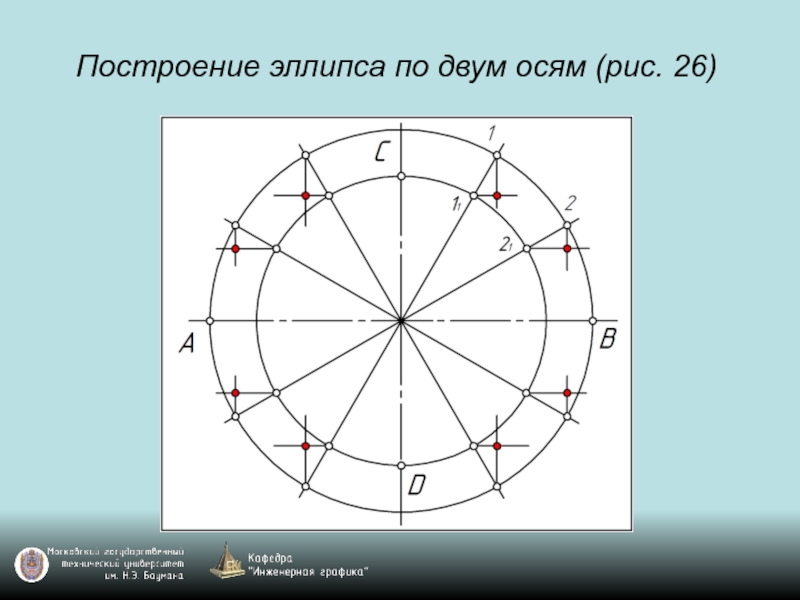
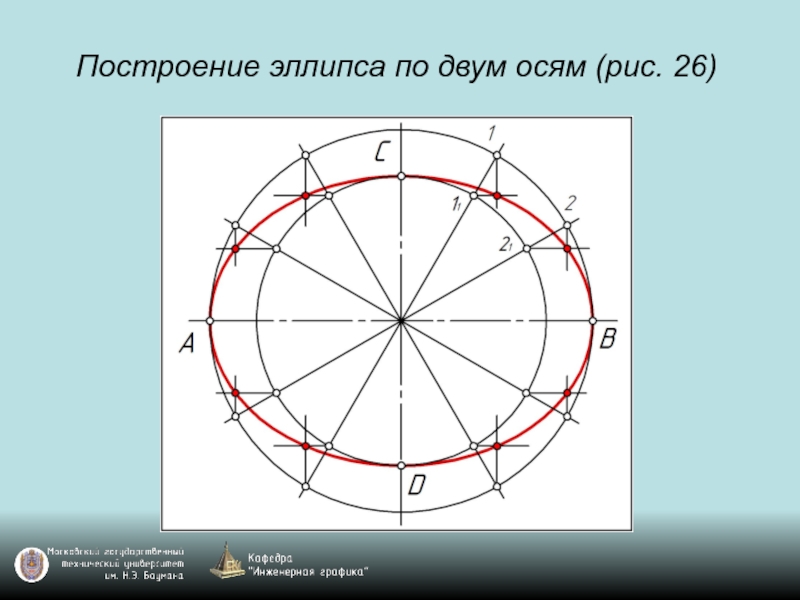
- 15. Построение эллипса по двум осям (рис. 26)
- 16. Построение эллипса по двум осям (рис. 26)
- 17. Построение эллипса по двум осям (рис. 26)
- 18. Построение эллипса по двум осям (рис. 26)
- 19. Построение эллипса по двум осям (рис. 26)
- 20. Построение эллипса по двум осям (рис. 26)
- 21. Построение эллипса по двум осям (рис. 26)
- 22. Построение эллипса по двум осям (рис. 26)
- 23. Построение эллипса по двум осям (рис. 26)
- 24. Построение эллипса по двум осям (рис. 26)
- 25. Построение эллипса по двум осям (рис. 26)
- 26. Построение эллипса по двум осям (рис. 26)
- 27. Построение эллипса по двум осям (рис. 26)
- 28. Построение эллипса по двум осям (рис. 26)
- 29. Пространственные кривые Винтовая линия Винтовая линия
- 30. Пространственные кривые Проекции винтовой линии (рис. 27)
- 31. Пространственные кривые Проекции винтовой линии (рис. 27)
- 32. Пространственные кривые Проекции винтовой линии (рис. 27)
- 33. Пространственные кривые Проекции винтовой линии (рис. 27)
- 34. Пространственные кривые Проекции винтовой линии (рис. 27)
- 35. Пространственные кривые Проекции винтовой линии (рис. 27)
- 36. Пространственные кривые Проекции винтовой линии (рис. 27)
- 37. Пространственные кривые Проекции винтовой линии (рис. 27)
- 38. Пространственные кривые Проекции винтовой линии (рис. 27)
- 39. 7. Образование и задание поверхностей Задание поверхности
- 40. Очерк поверхности Для большей наглядности в ряде случаев используют очерк поверхности (рис. 30).
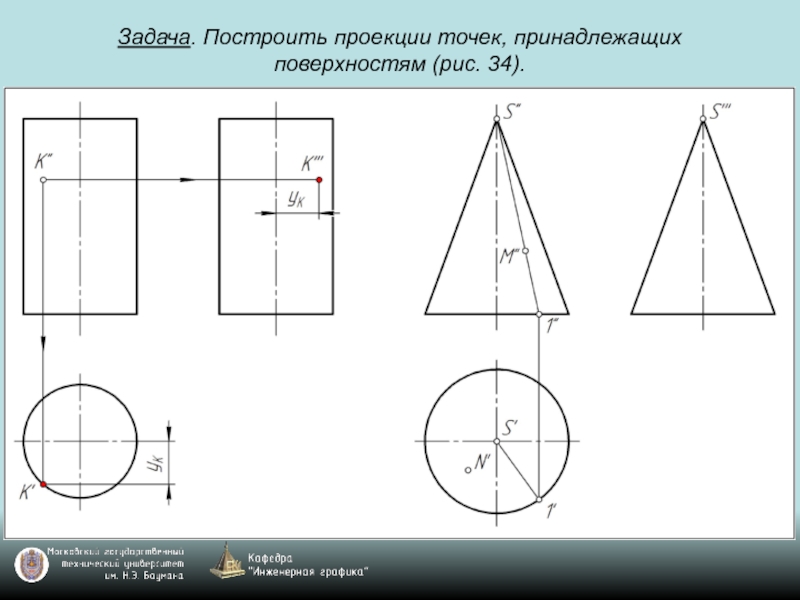
- 41. Общее правило построения проекции точки, принадлежащей поверхности:
- 42. Обзор поверхностей Можно группировать поверхности: по форме
- 43. Одна и та же поверхность может быть
- 44. Одна и та же поверхность может быть
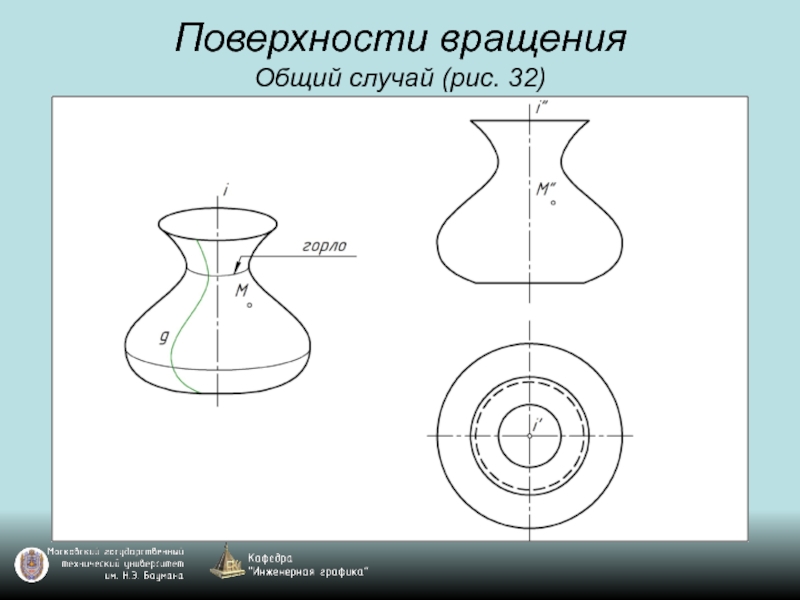
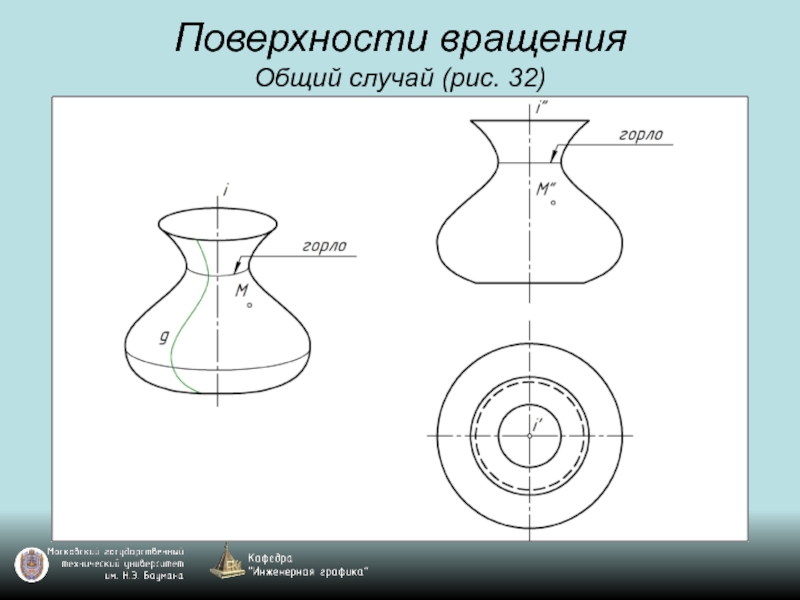
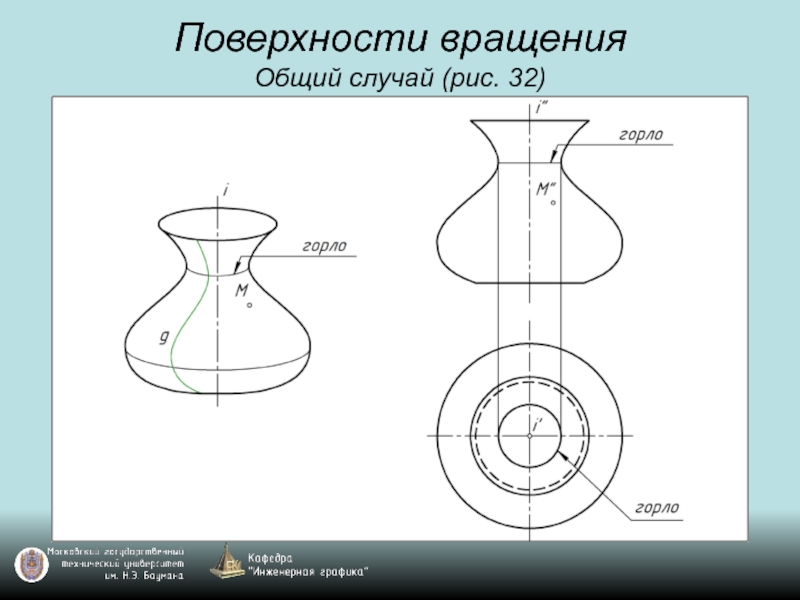
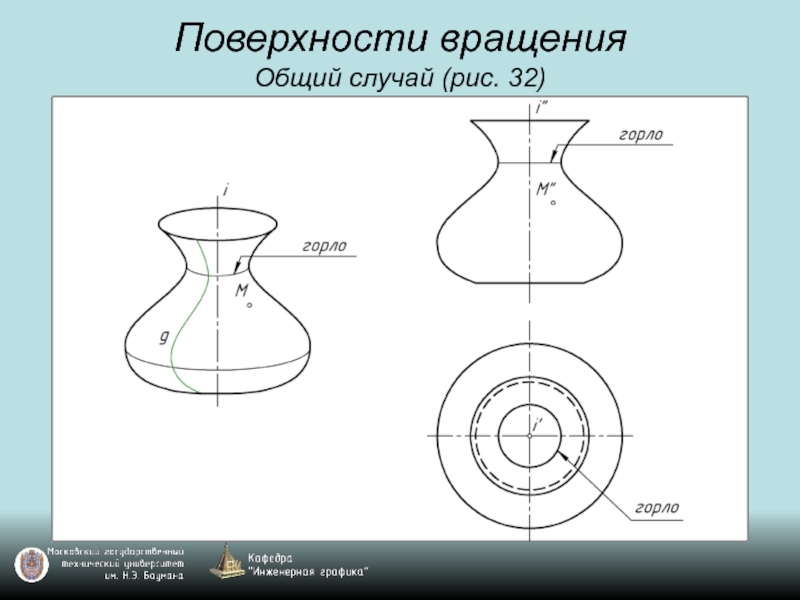
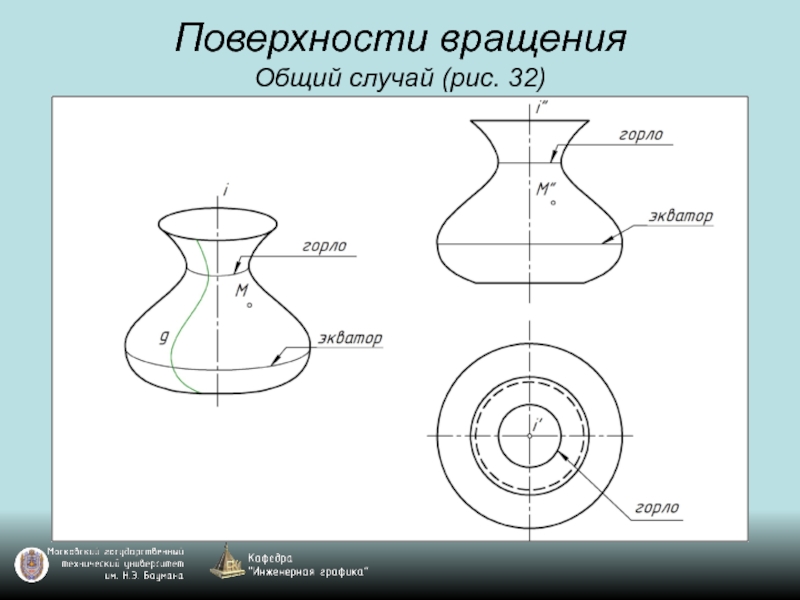
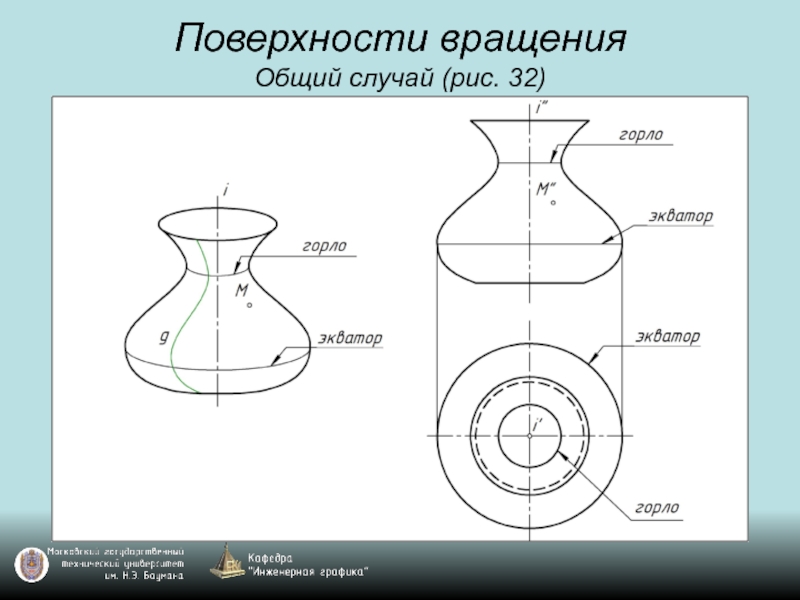
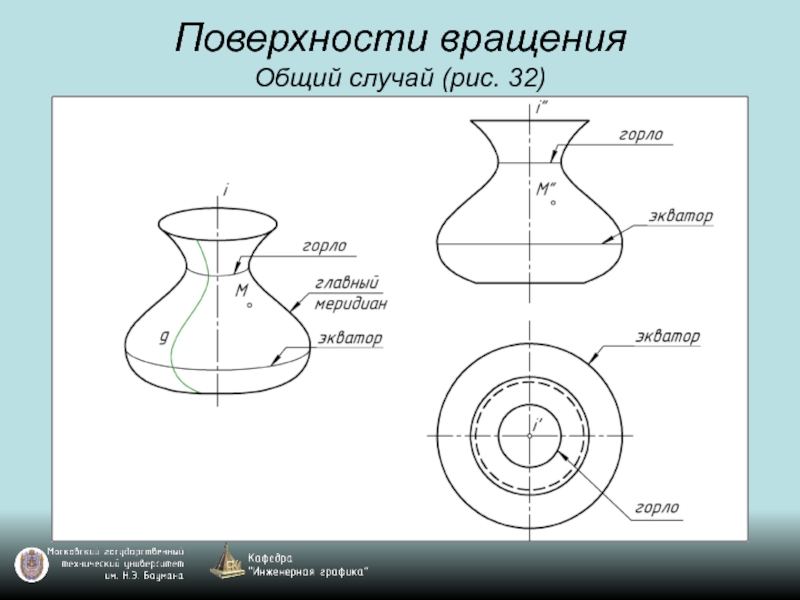
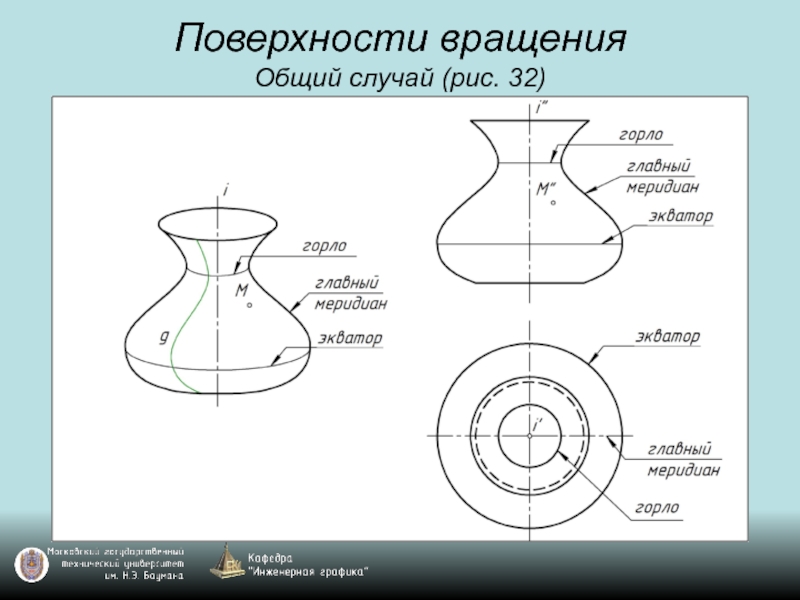
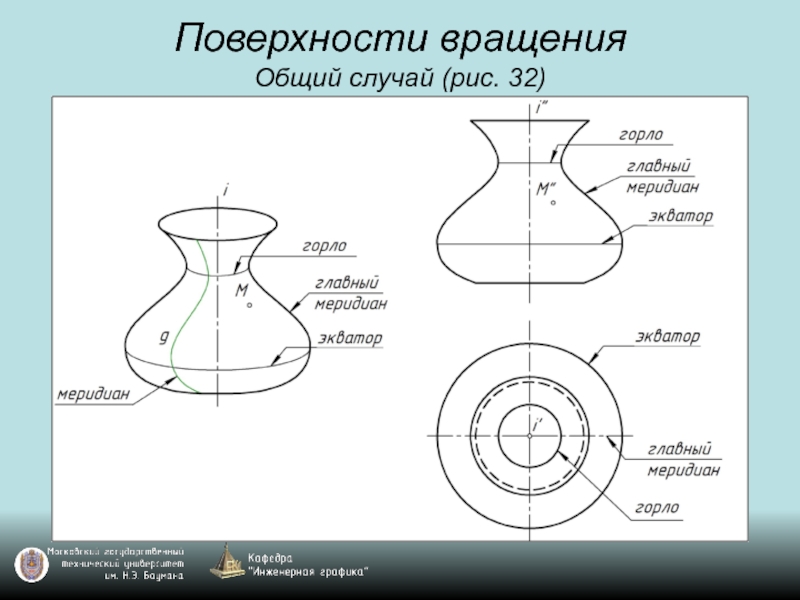
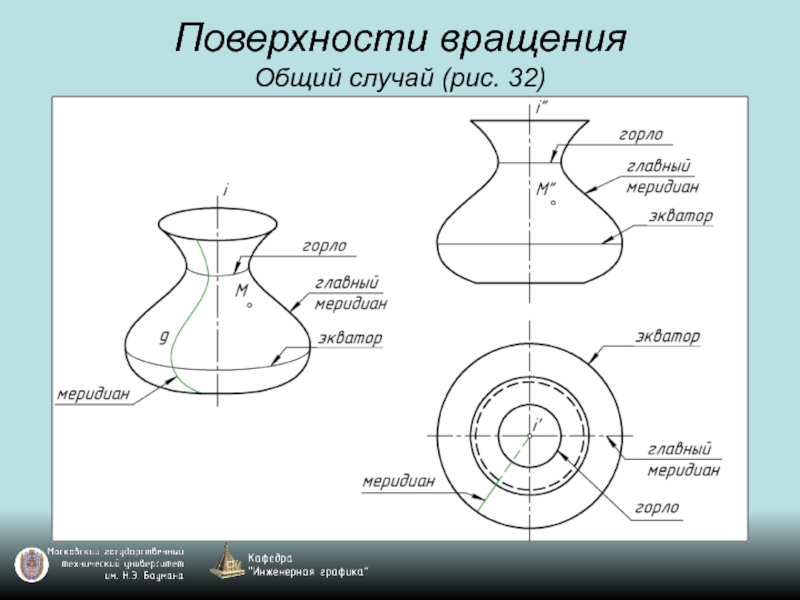
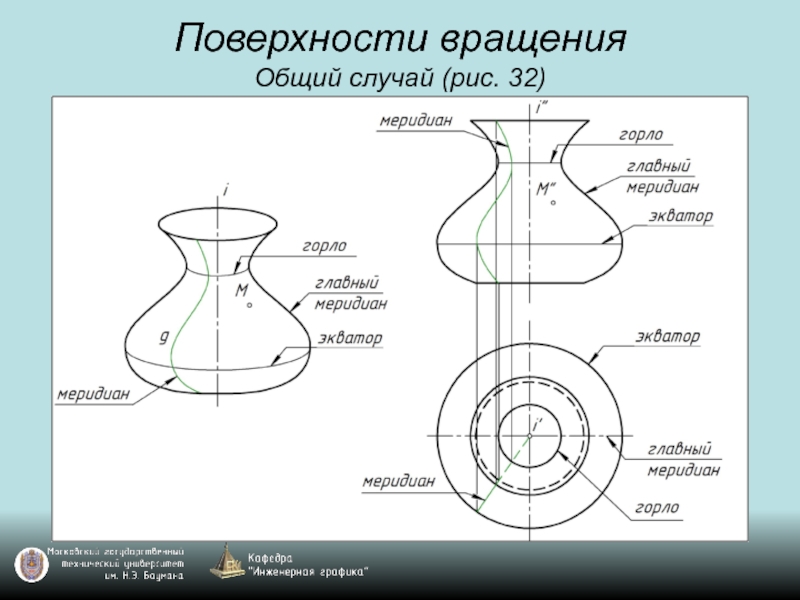
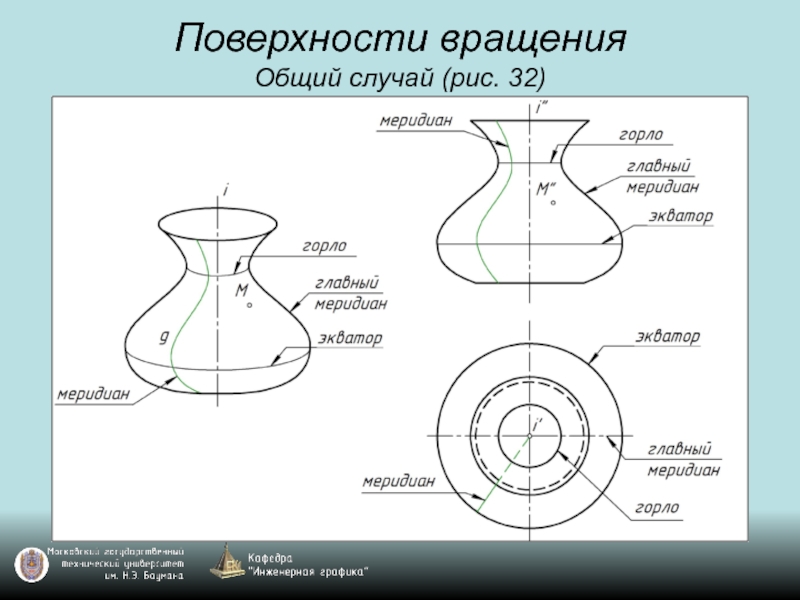
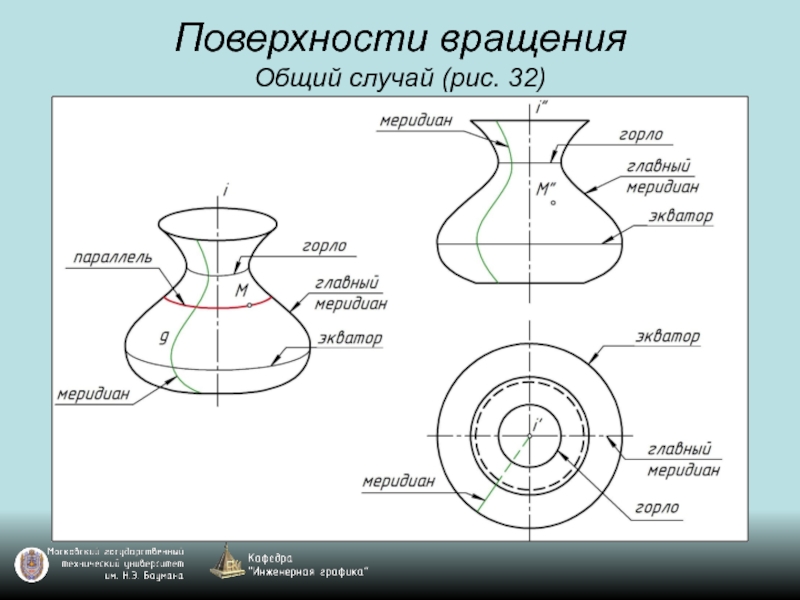
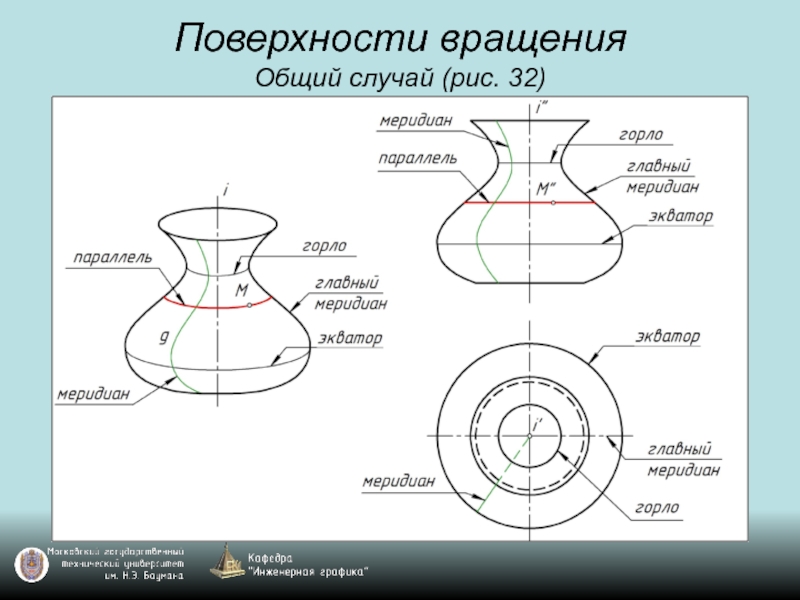
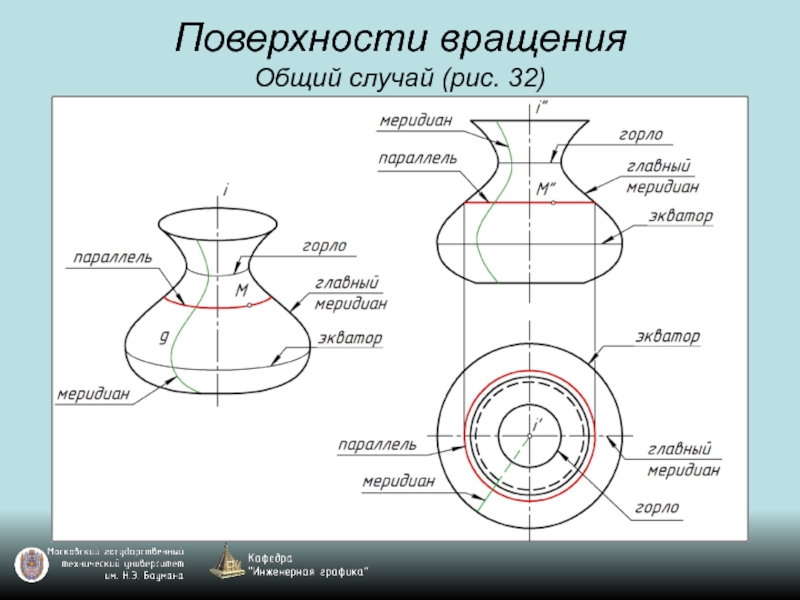
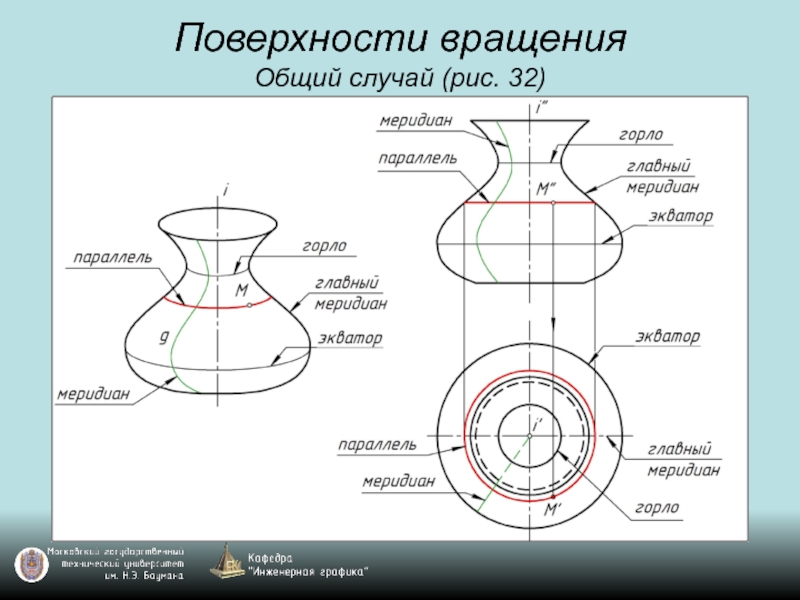
- 45. Поверхности вращения Общий случай (рис. 32)
- 46. Поверхности вращения Общий случай (рис. 32)
- 47. Поверхности вращения Общий случай (рис. 32)
- 48. Поверхности вращения Общий случай (рис. 32)
- 49. Поверхности вращения Общий случай (рис. 32)
- 50. Поверхности вращения Общий случай (рис. 32)
- 51. Поверхности вращения Общий случай (рис. 32)
- 52. Поверхности вращения Общий случай (рис. 32)
- 53. Поверхности вращения Общий случай (рис. 32)
- 54. Поверхности вращения Общий случай (рис. 32)
- 55. Поверхности вращения Общий случай (рис. 32)
- 56. Поверхности вращения Общий случай (рис. 32)
- 57. Поверхности вращения Общий случай (рис. 32)
- 58. Поверхности вращения Общий случай (рис. 32)
- 59. Поверхности вращения Общий случай (рис. 32)
- 60. Поверхности вращения Общий случай (рис. 32)
- 61. Поверхности вращения Общий случай (рис. 32)
- 62. Поверхности вращения Общий случай (рис. 32)
- 63. Поверхности вращения Общий случай (рис. 32)
- 64. Поверхности вращения Общий случай (рис. 32)
- 65. Поверхности вращения с образующей g – прямой
- 66. Поверхности вращения с образующей g – прямой
- 67. Поверхности вращения с образующей g – прямой
- 68. Поверхности вращения с образующей g – прямой
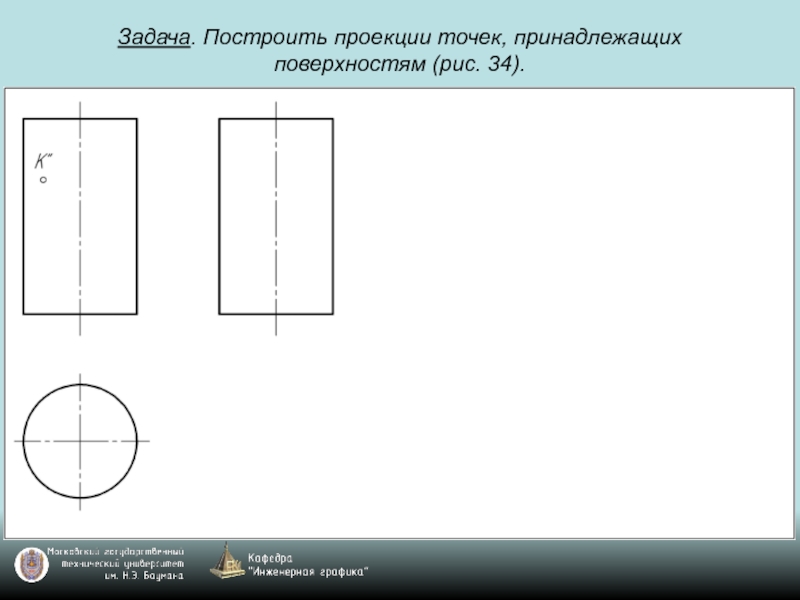
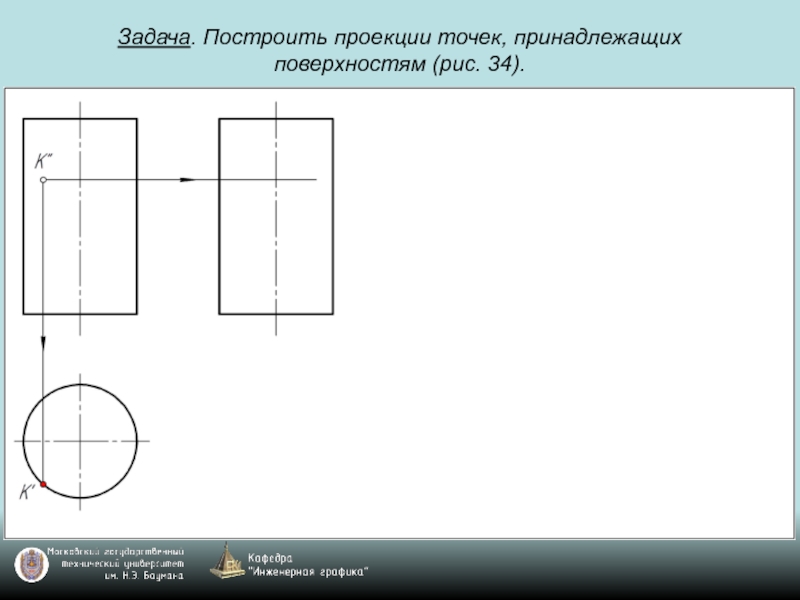
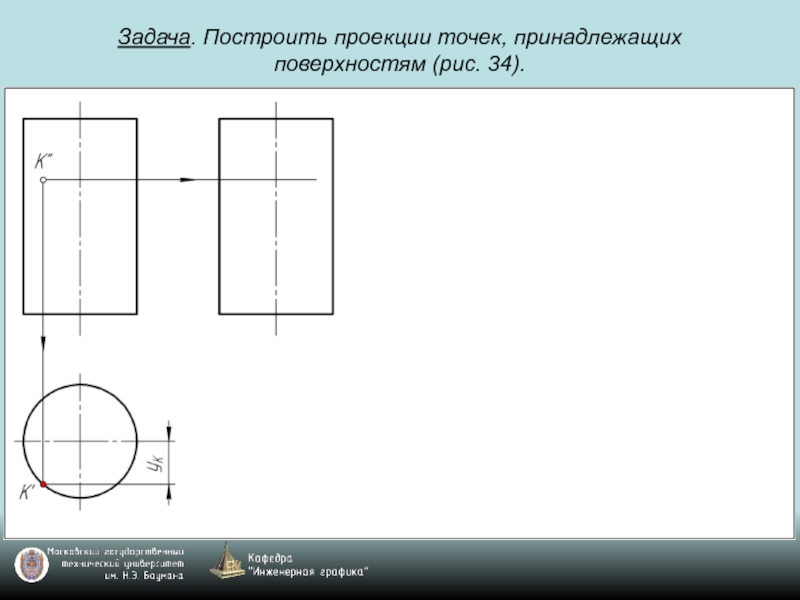
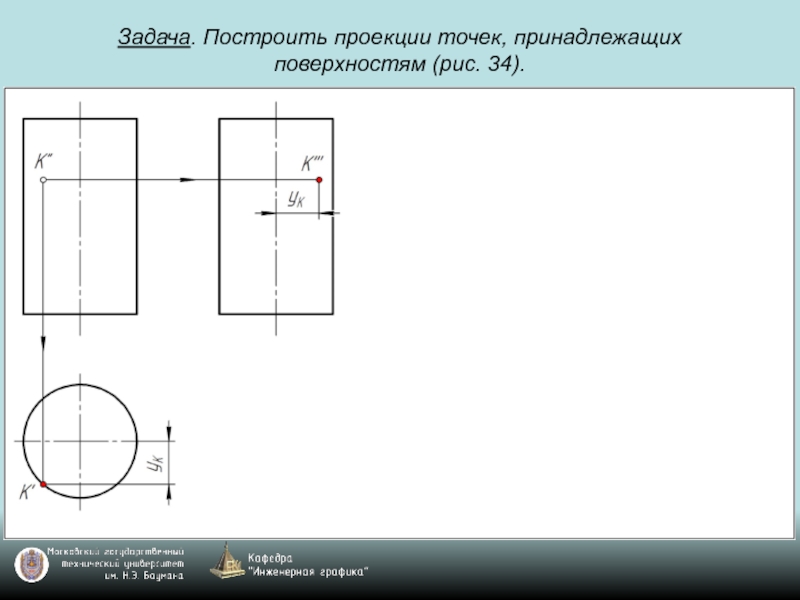
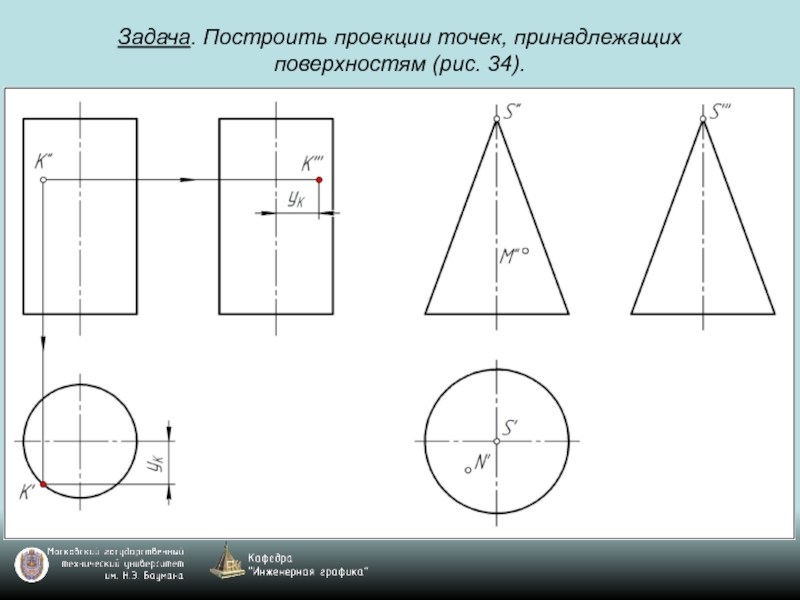
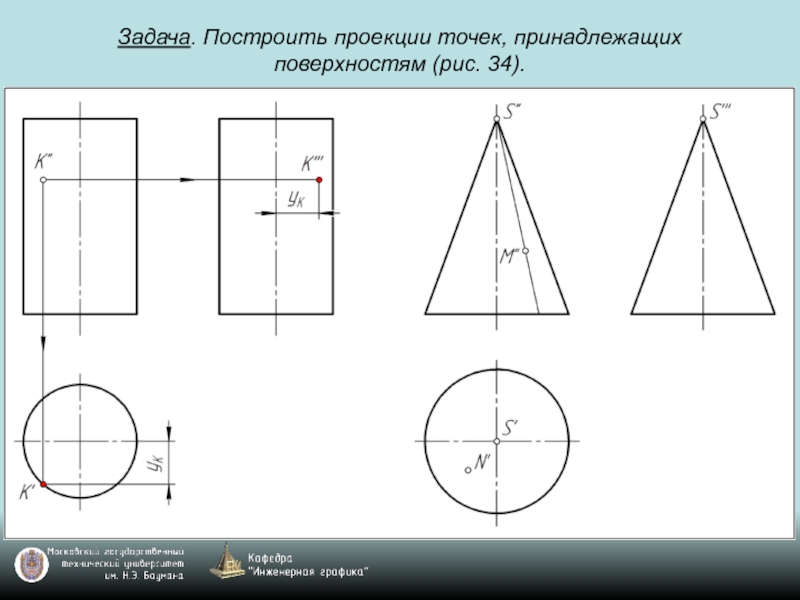
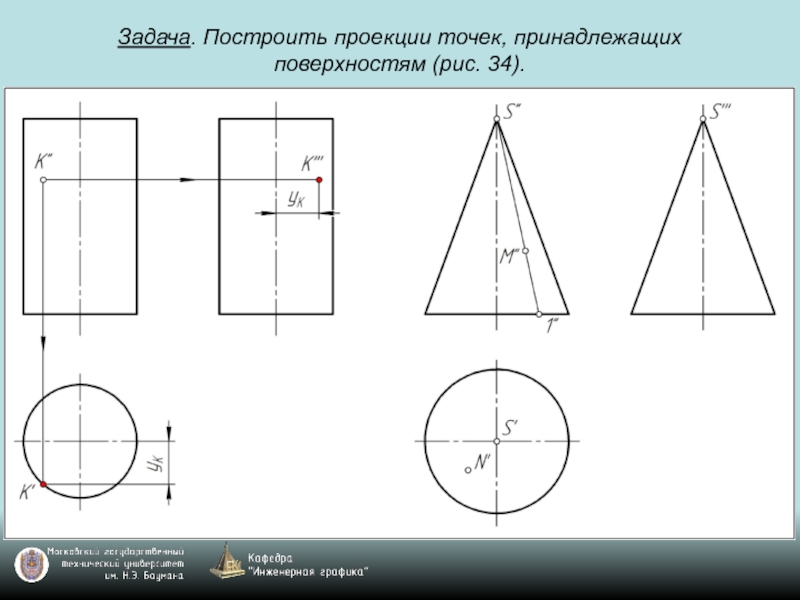
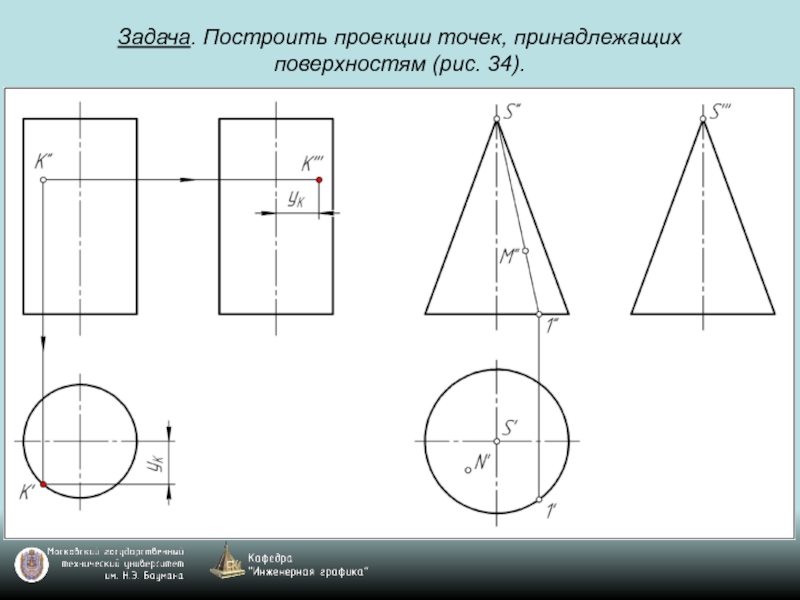
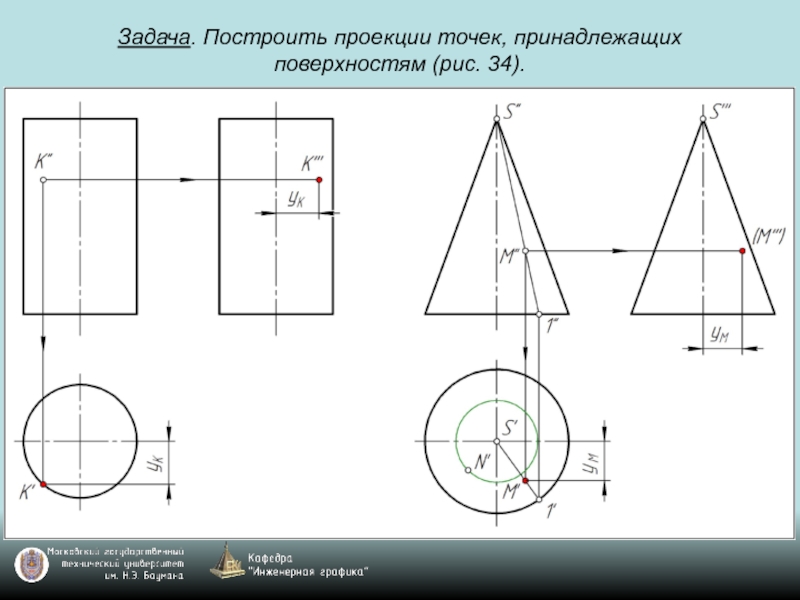
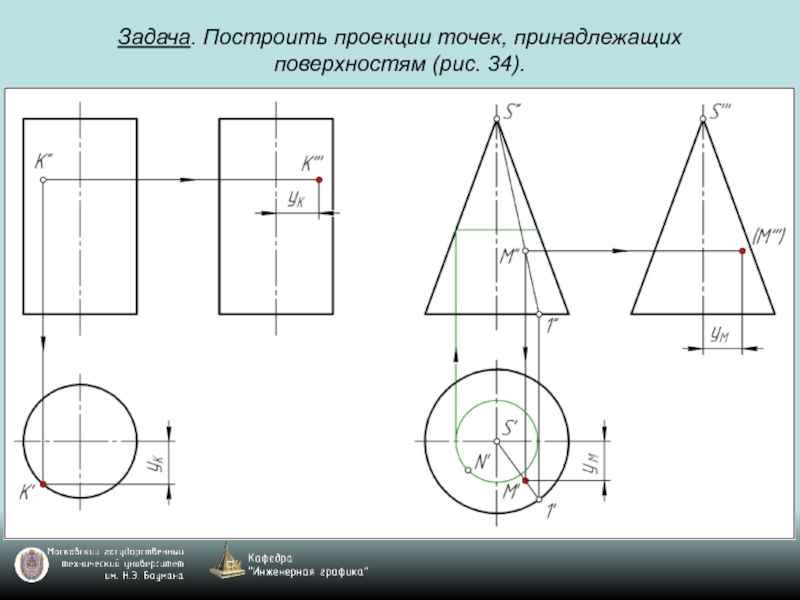
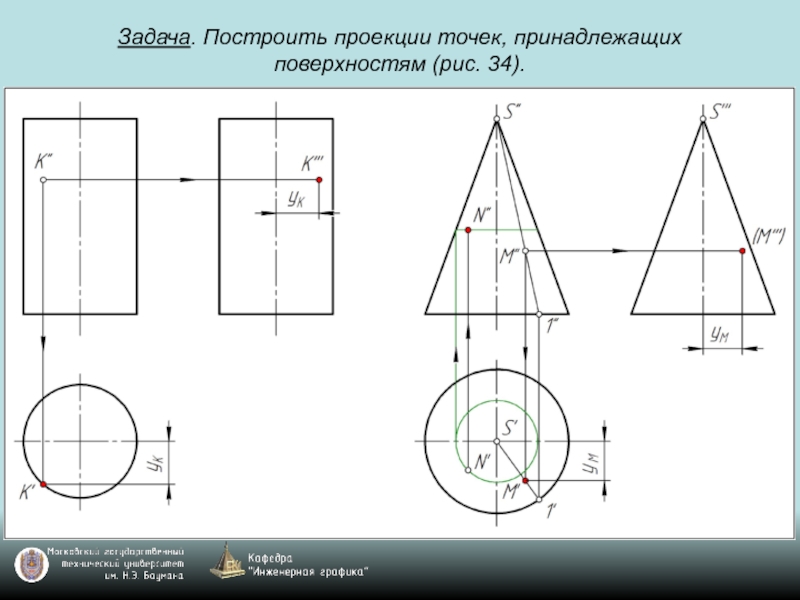
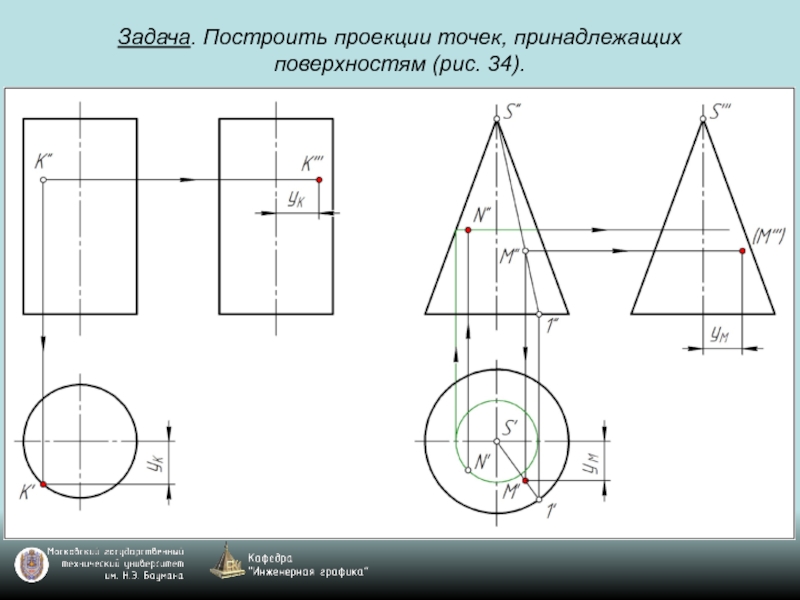
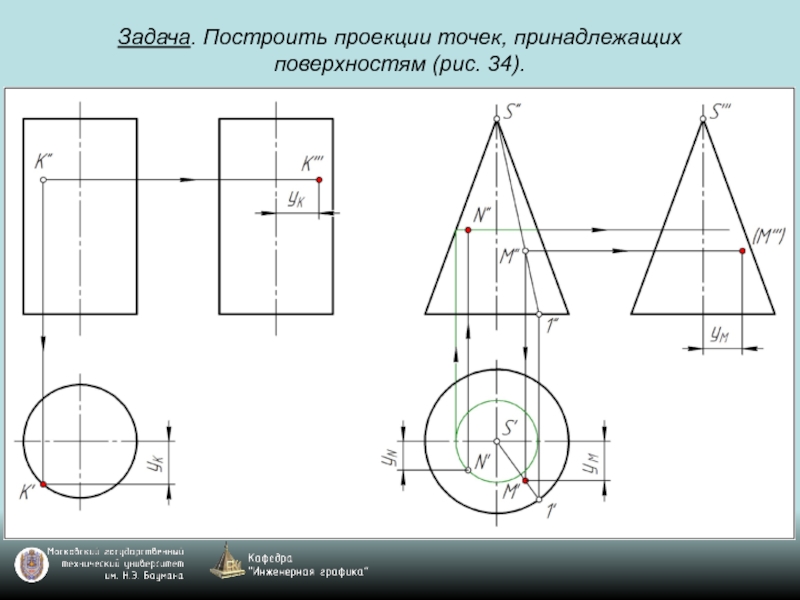
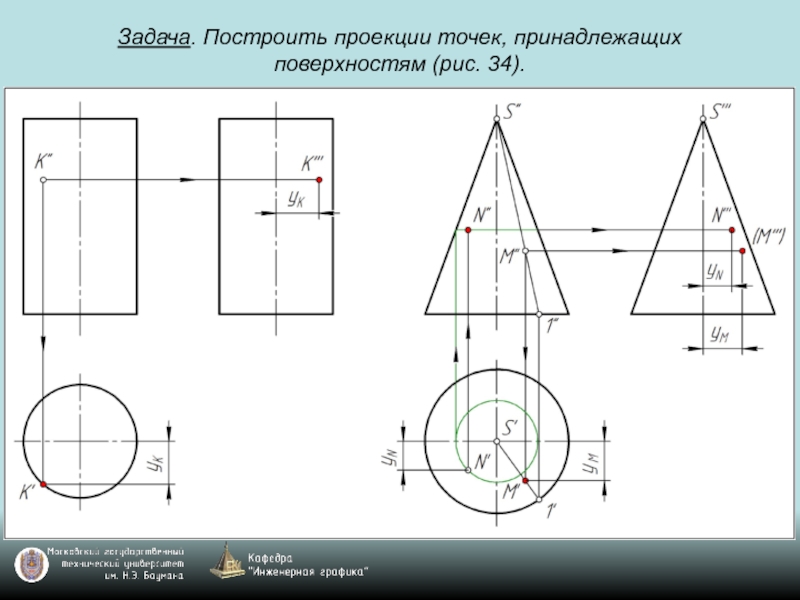
- 69. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
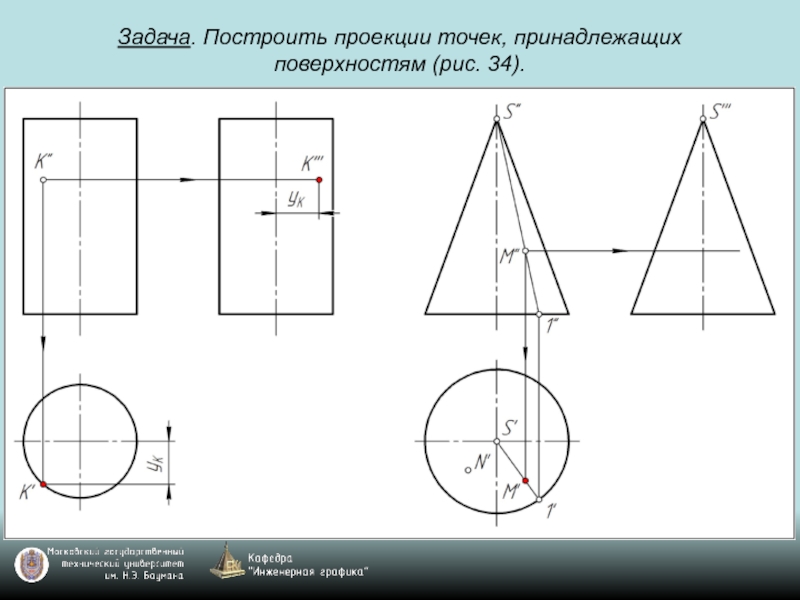
- 70. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
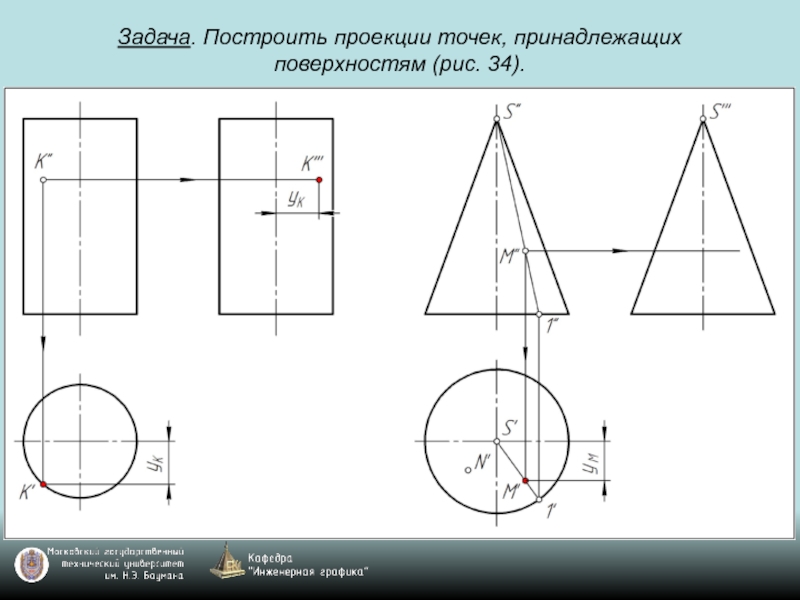
- 71. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
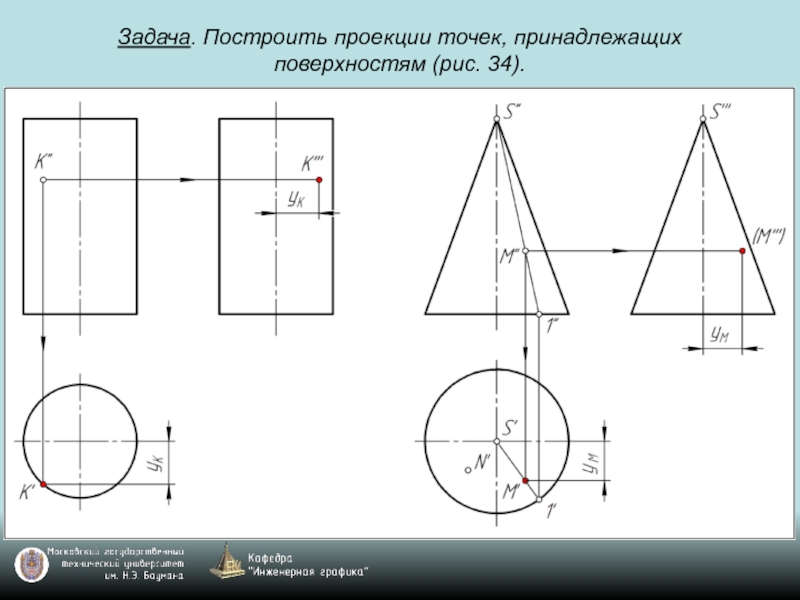
- 72. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
- 73. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
- 74. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
- 75. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
- 76. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
- 77. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
- 78. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
- 79. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
- 80. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
- 81. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
- 82. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
- 83. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
- 84. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
- 85. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
- 86. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
- 87. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
- 88. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
- 89. Поверхности вращения с образующей g – дугой
- 90. Поверхности вращения с образующей g – дугой
- 91. Поверхности вращения с образующей g – дугой
- 92. Поверхности вращения с образующей g – дугой
- 93. Поверхности вращения с образующей g – дугой
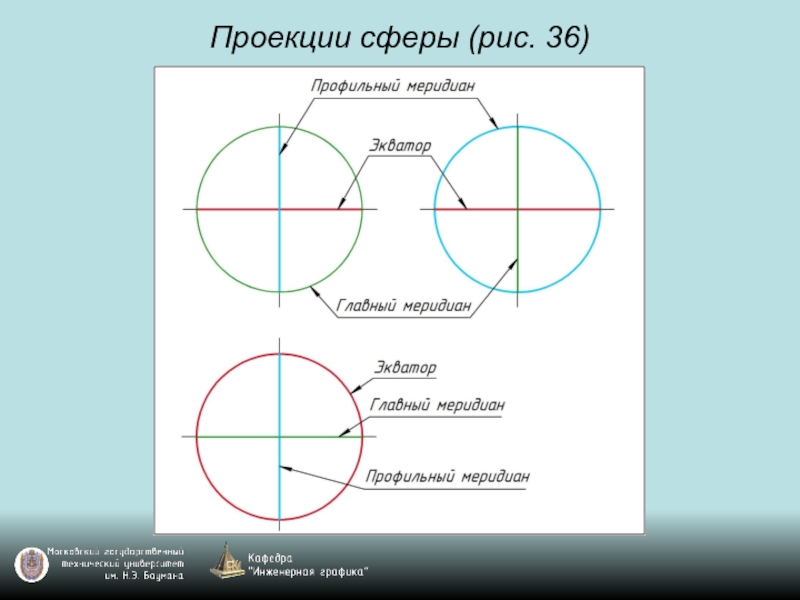
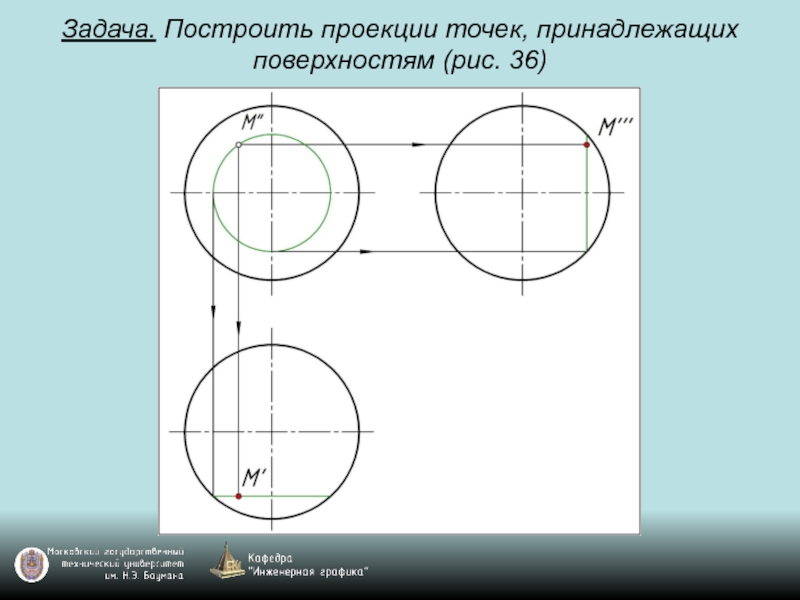
- 94. Проекции сферы (рис. 36)
- 95. Проекции сферы (рис. 36)
- 96. Проекции сферы (рис. 36)
- 97. Проекции сферы (рис. 36)
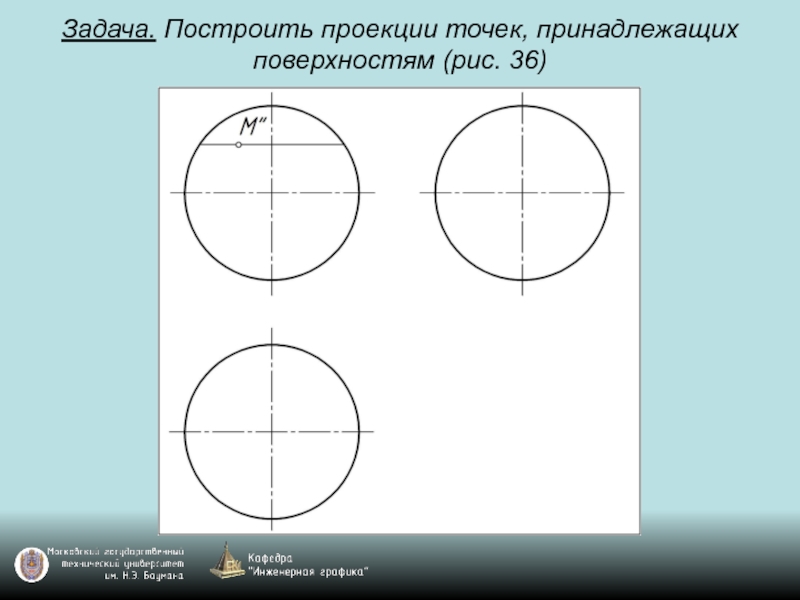
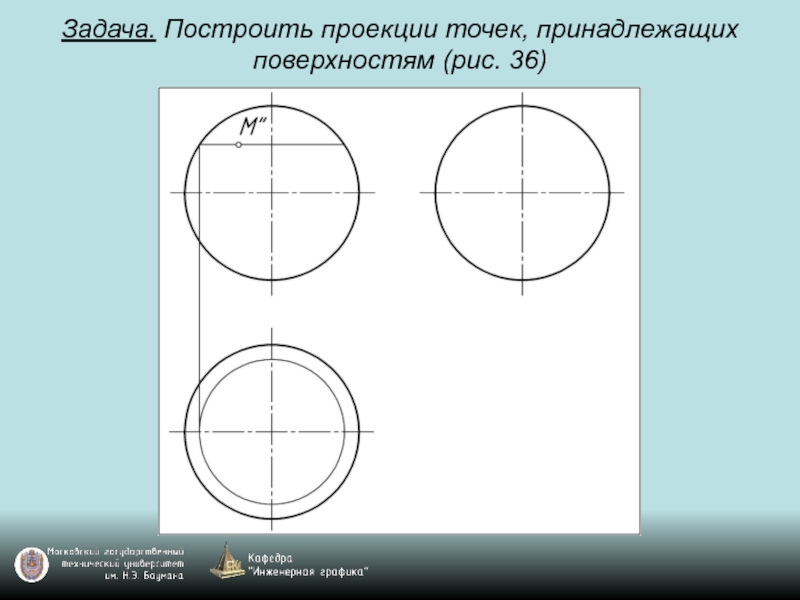
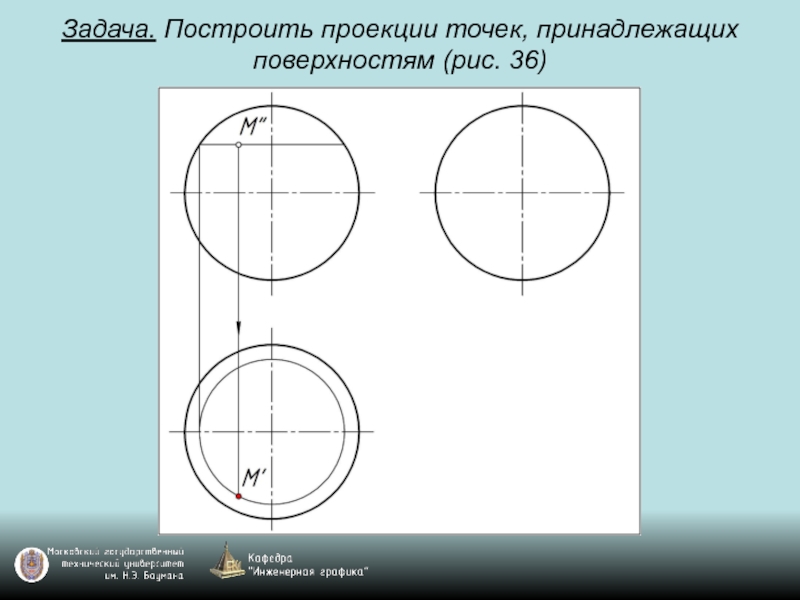
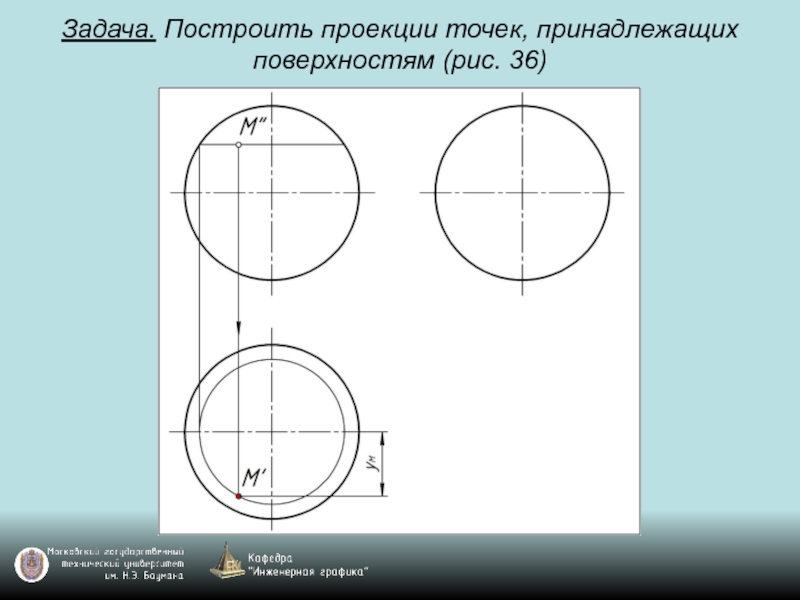
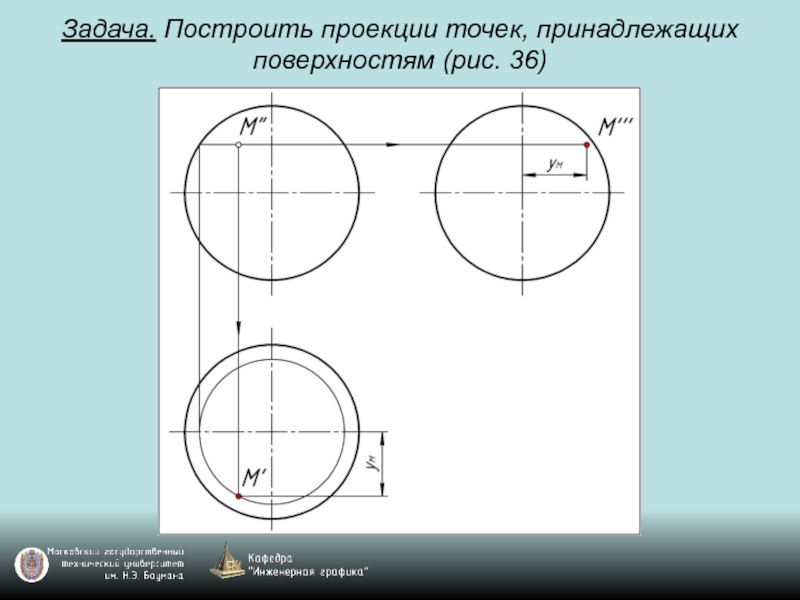
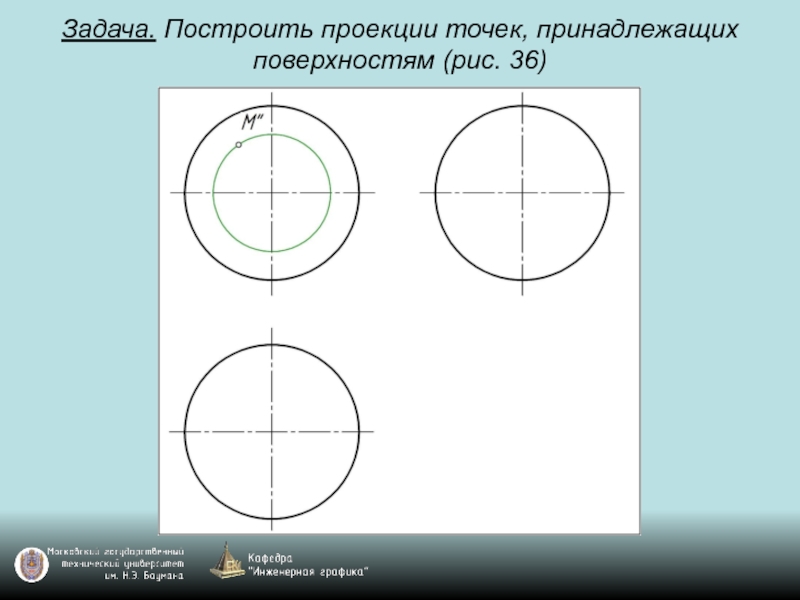
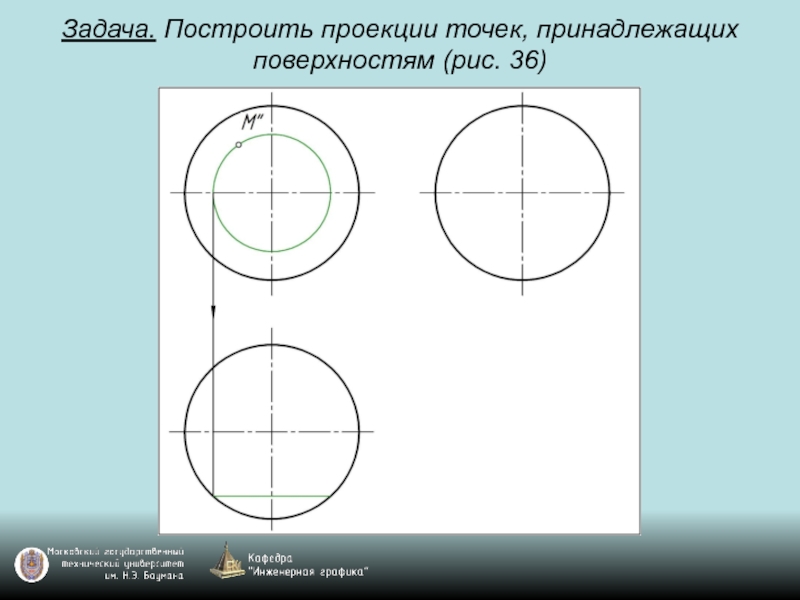
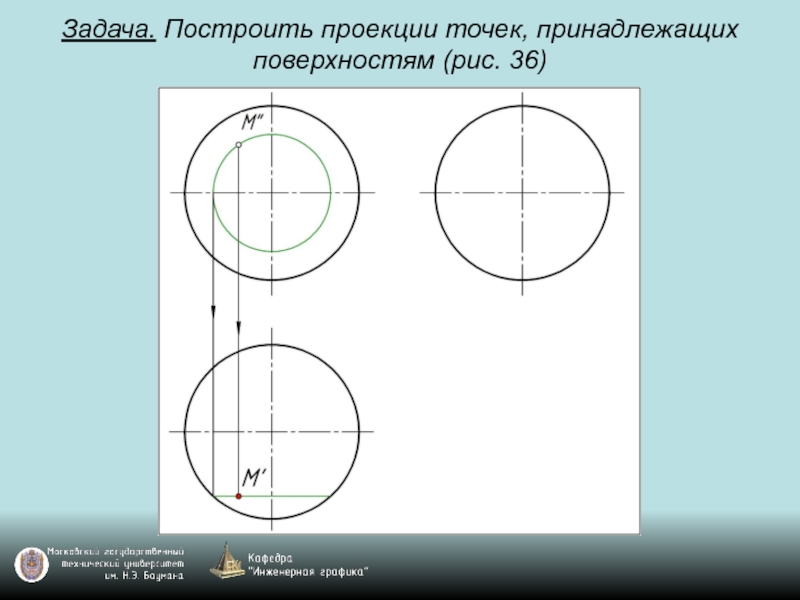
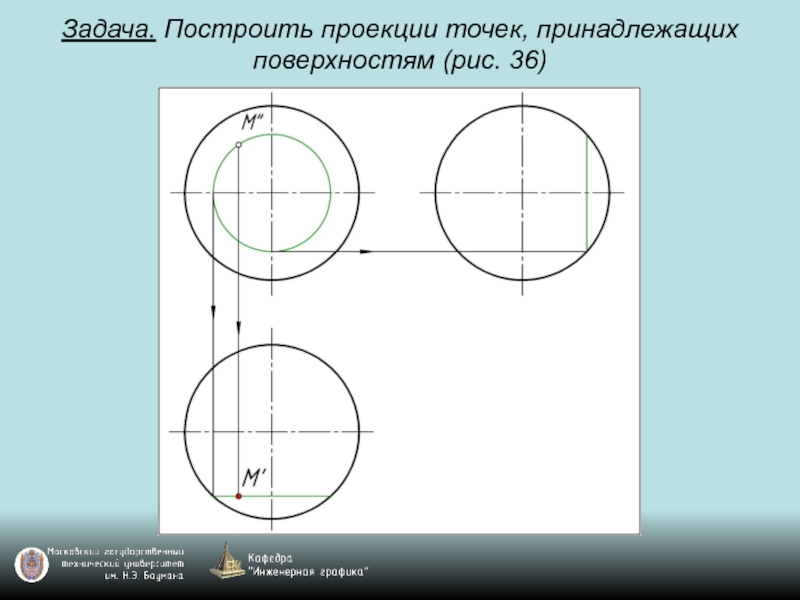
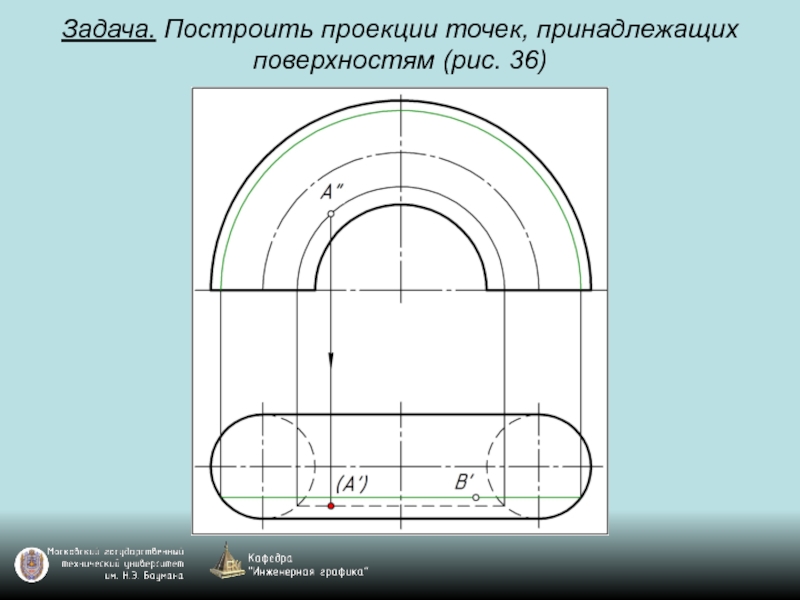
- 98. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 99. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 100. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 101. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 102. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 103. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 104. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 105. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 106. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 107. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 108. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 109. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 110. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 111. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 112. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 113. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 114. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 115. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 116. Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
- 117. Винтовые поверхности Винтовая поверхность
- 118. Чаще всего в технике применяют в качестве
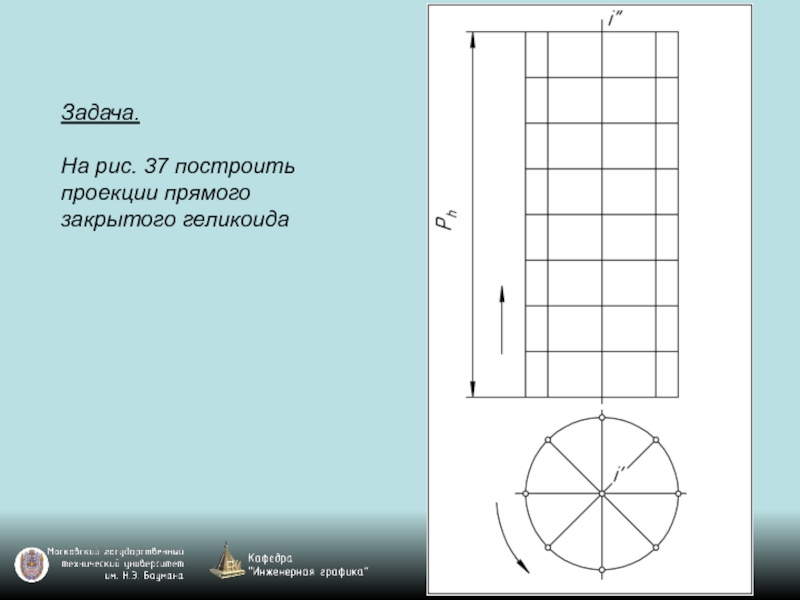
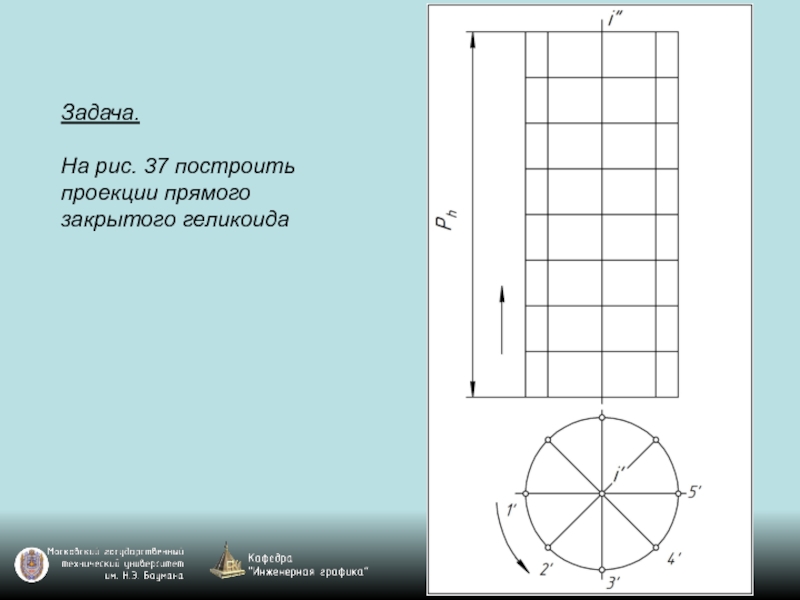
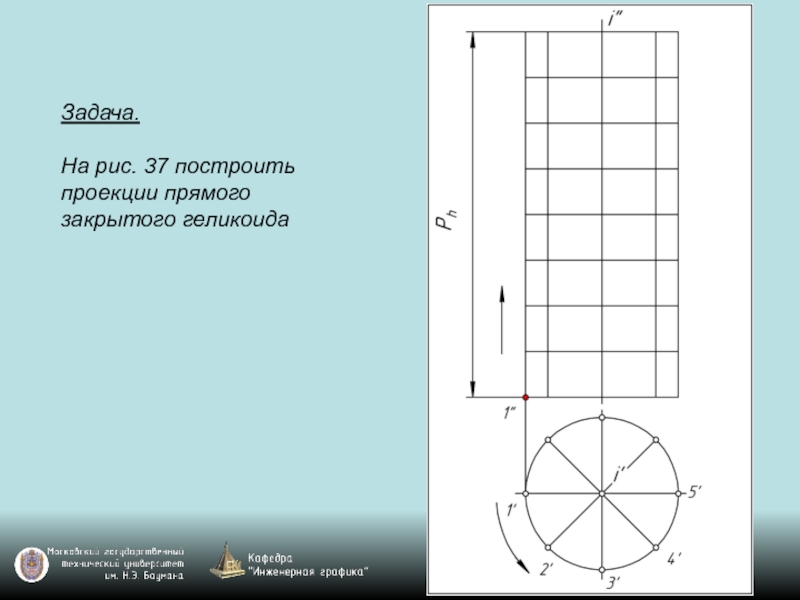
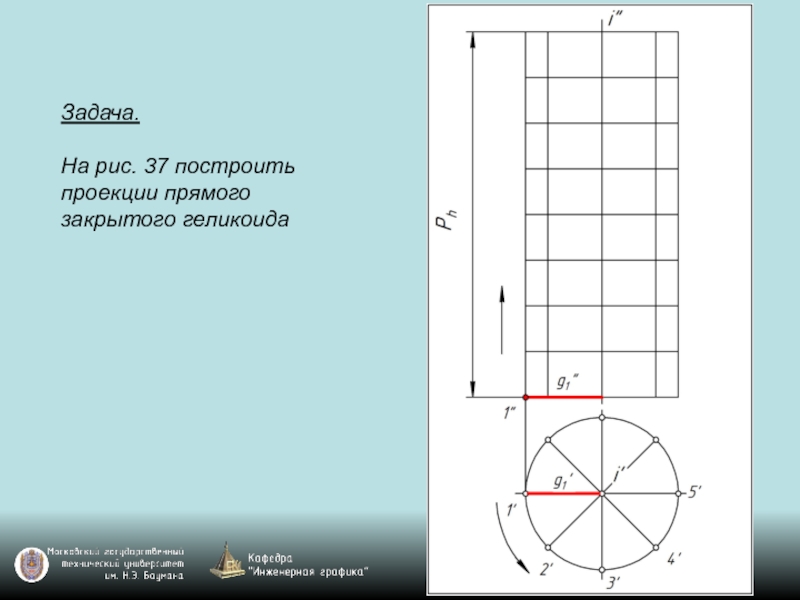
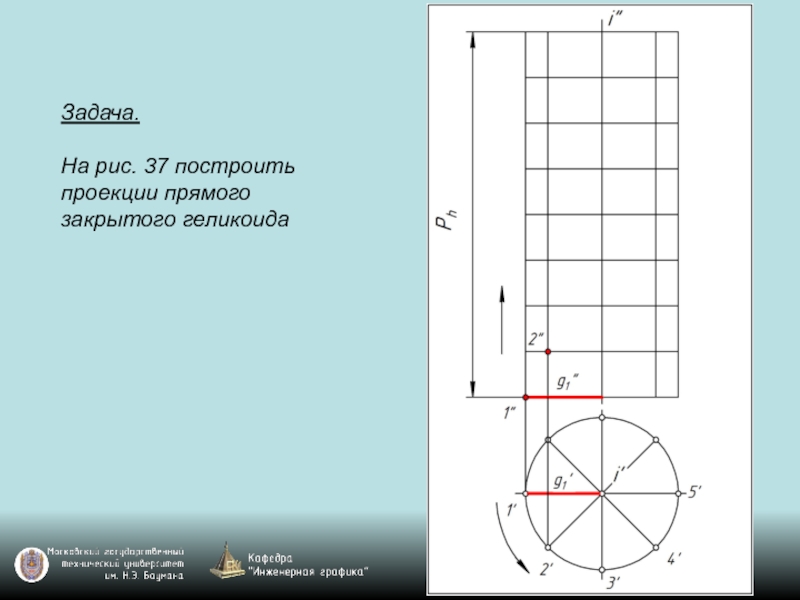
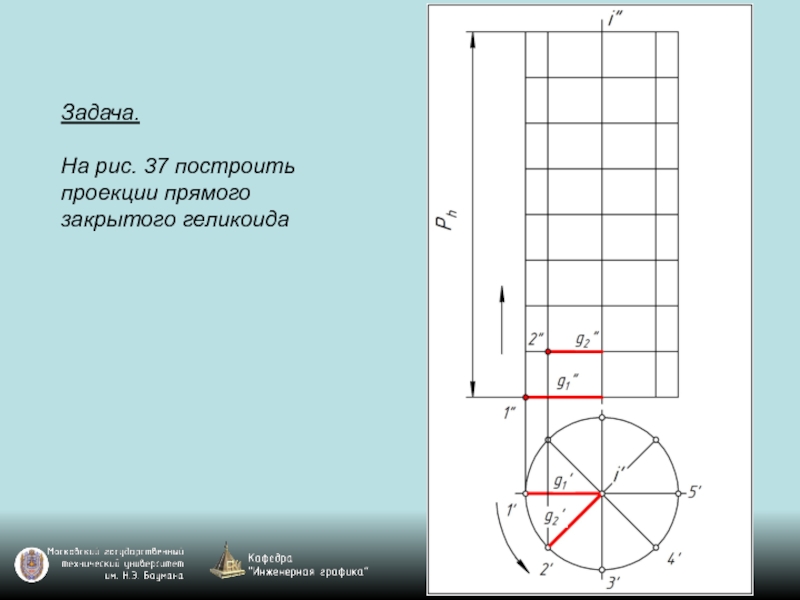
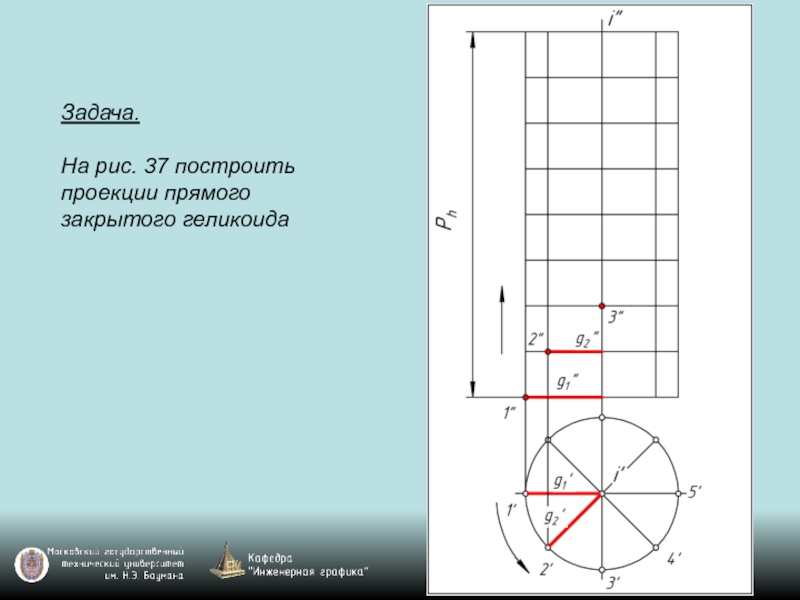
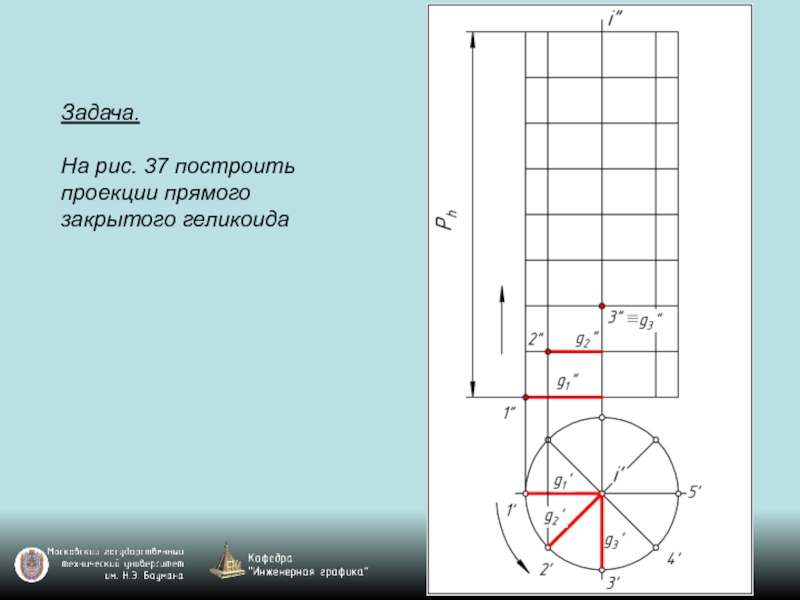
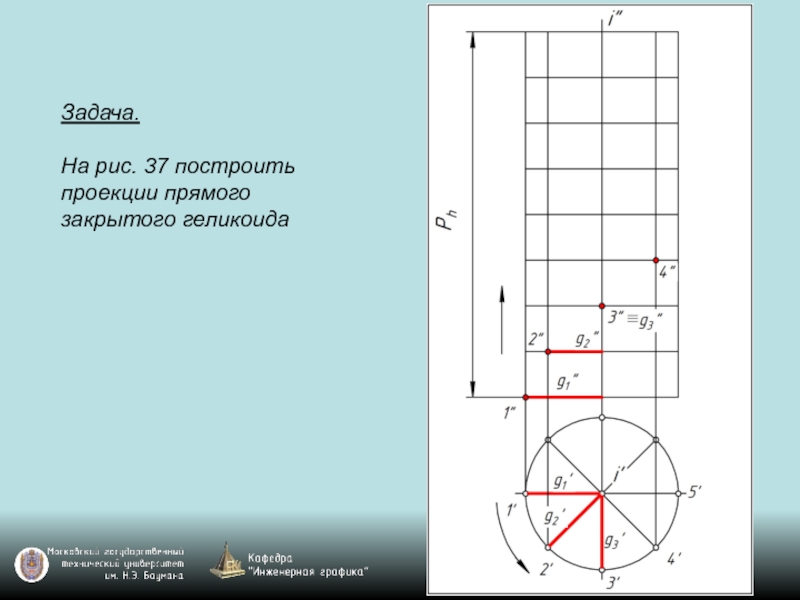
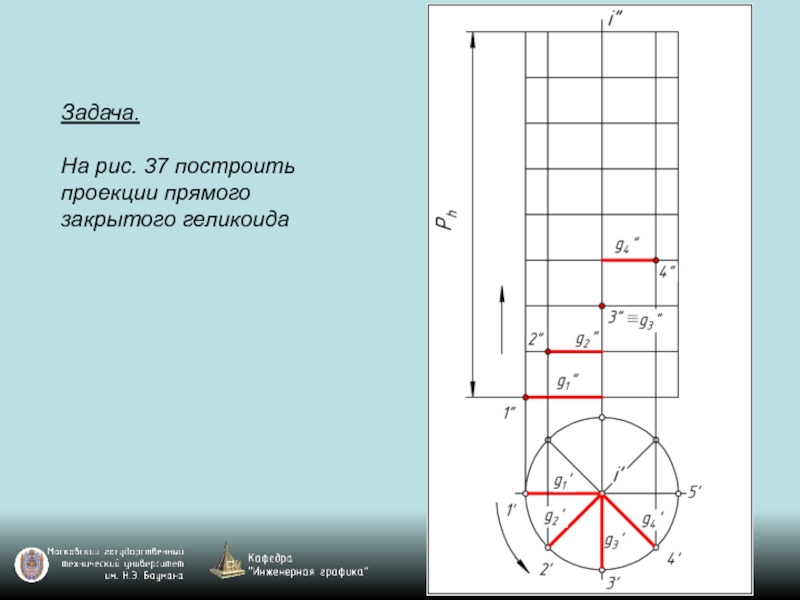
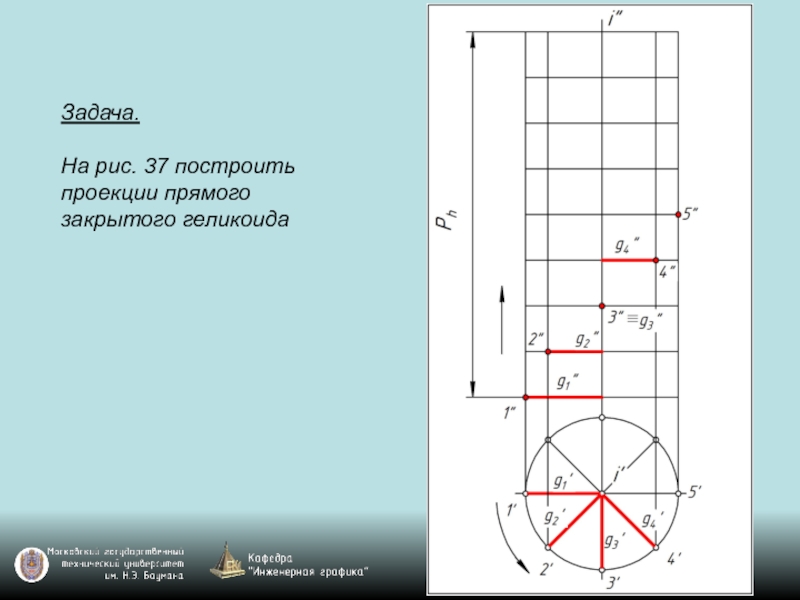
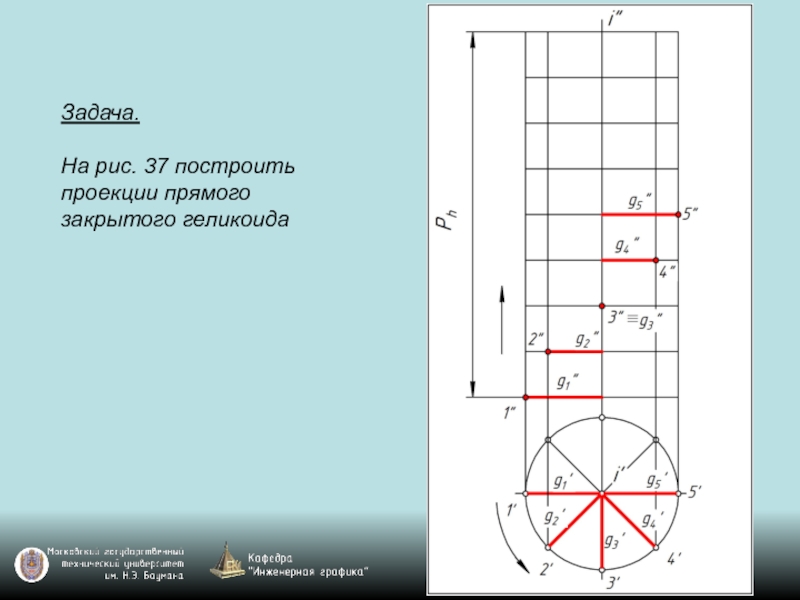
- 119. Задача. На рис. 37 построить проекции прямого закрытого геликоида
- 120. Задача. На рис. 37 построить проекции прямого закрытого геликоида
- 121. Задача. На рис. 37 построить проекции прямого закрытого геликоида
- 122. Задача. На рис. 37 построить проекции прямого закрытого геликоида
- 123. Задача. На рис. 37 построить проекции прямого закрытого геликоида
- 124. Задача. На рис. 37 построить проекции прямого закрытого геликоида
- 125. Задача. На рис. 37 построить проекции прямого закрытого геликоида
- 126. Задача. На рис. 37 построить проекции прямого закрытого геликоида
- 127. Задача. На рис. 37 построить проекции прямого закрытого геликоида
- 128. Задача. На рис. 37 построить проекции прямого закрытого геликоида
- 129. Задача. На рис. 37 построить проекции прямого закрытого геликоида
- 130. Задача. На рис. 37 построить проекции прямого закрытого геликоида
- 131. Задача. На рис. 37 построить проекции прямого закрытого геликоида
- 132. Задача. На рис. 37 построить проекции прямого закрытого геликоида
- 133. Задача. На рис. 37 построить проекции прямого закрытого геликоида
- 134. Рис. 38а. Наклонный (косой) закрытый геликоид (Архимедов винт)
- 135. Рис. 38б. Прямой открытый геликоид
Слайд 1ЛЕКЦИЯ 3
Кривые линии.
Образование и задание поверхностей.
Начертательная геометрия
1 семестр
для студентов ф-та ИУ
Подготовили:
доценты
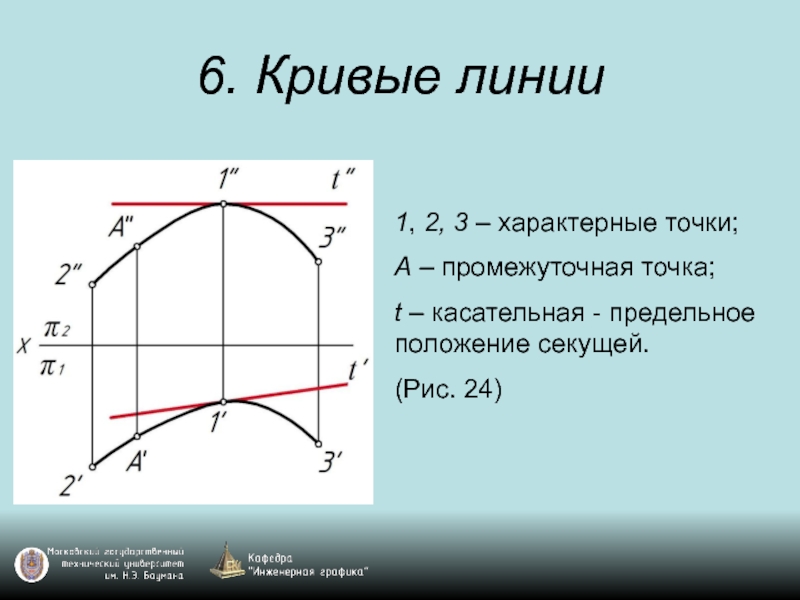
Слайд 26. Кривые линии
1, 2, 3 – характерные точки;
А – промежуточная точка;
t
– касательная - предельное положение секущей.
(Рис. 24)
(Рис. 24)
Слайд 29Пространственные кривые
Винтовая линия
Винтовая линия образуется при винтовом движении точки, т.е. при
повороте точки вокруг неподвижной оси и одновременном перемещении точки вдоль оси.
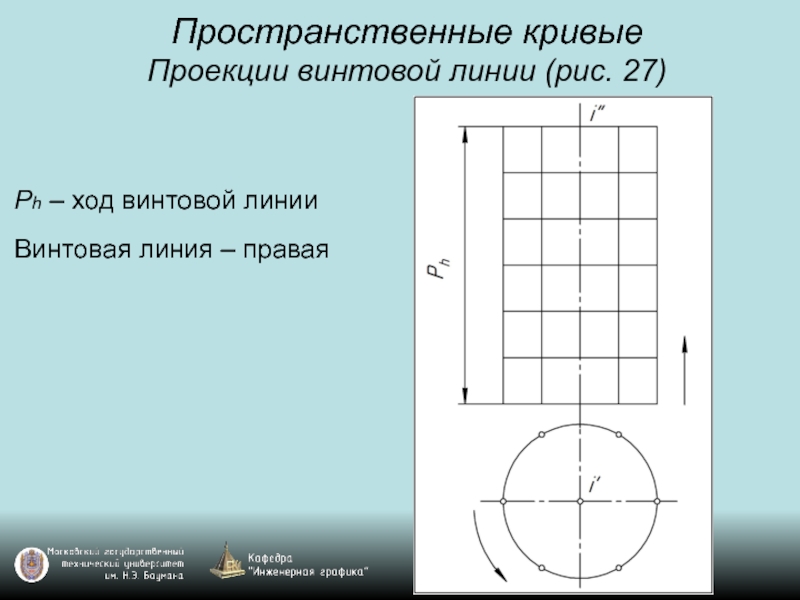
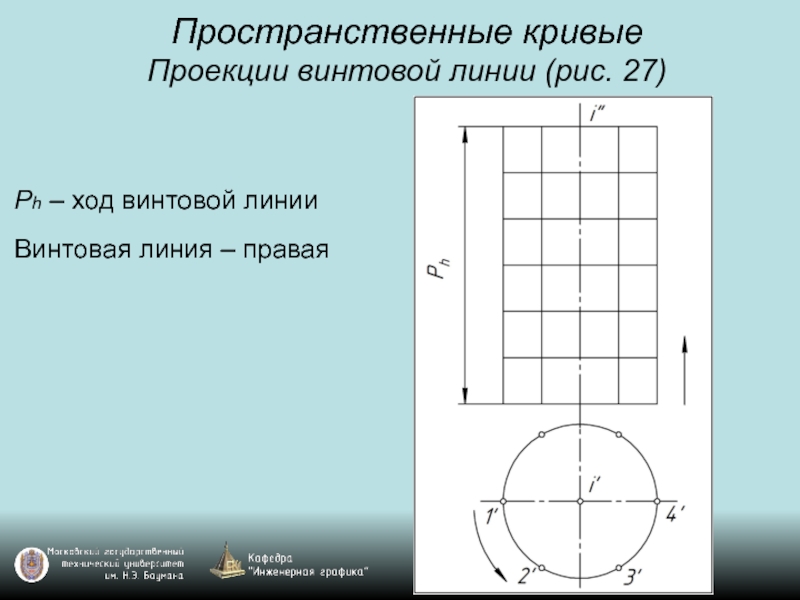
Слайд 30Пространственные кривые
Проекции винтовой линии (рис. 27)
Ph – ход винтовой линии
Винтовая линия
– правая
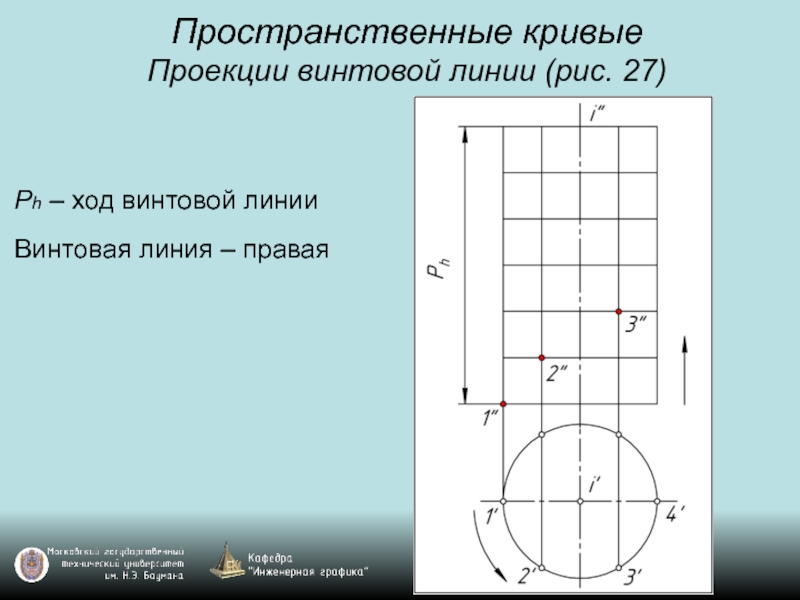
Слайд 31Пространственные кривые
Проекции винтовой линии (рис. 27)
Ph – ход винтовой линии
Винтовая линия
– правая
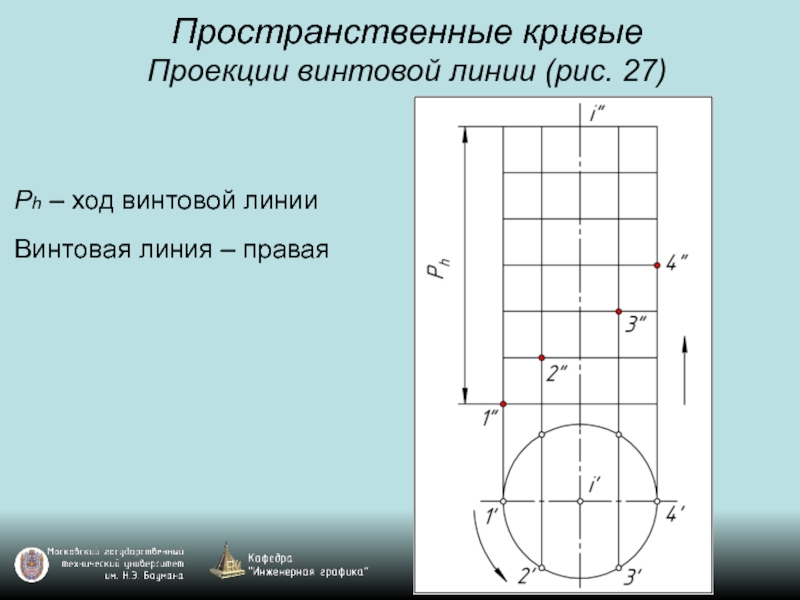
Слайд 32Пространственные кривые
Проекции винтовой линии (рис. 27)
Ph – ход винтовой линии
Винтовая линия
– правая
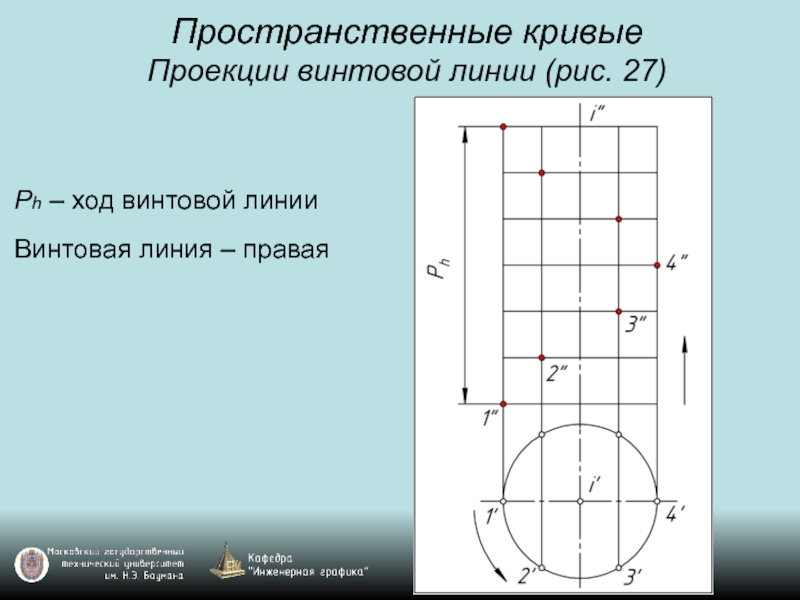
Слайд 33Пространственные кривые
Проекции винтовой линии (рис. 27)
Ph – ход винтовой линии
Винтовая линия
– правая
Слайд 34Пространственные кривые
Проекции винтовой линии (рис. 27)
Ph – ход винтовой линии
Винтовая линия
– правая
Слайд 35Пространственные кривые
Проекции винтовой линии (рис. 27)
Ph – ход винтовой линии
Винтовая линия
– правая
Слайд 36Пространственные кривые
Проекции винтовой линии (рис. 27)
Ph – ход винтовой линии
Винтовая линия
– правая
Слайд 37Пространственные кривые
Проекции винтовой линии (рис. 27)
Ph – ход винтовой линии
Винтовая линия
– правая
Слайд 38Пространственные кривые
Проекции винтовой линии (рис. 27)
Ph – ход винтовой линии
Винтовая линия
– правая
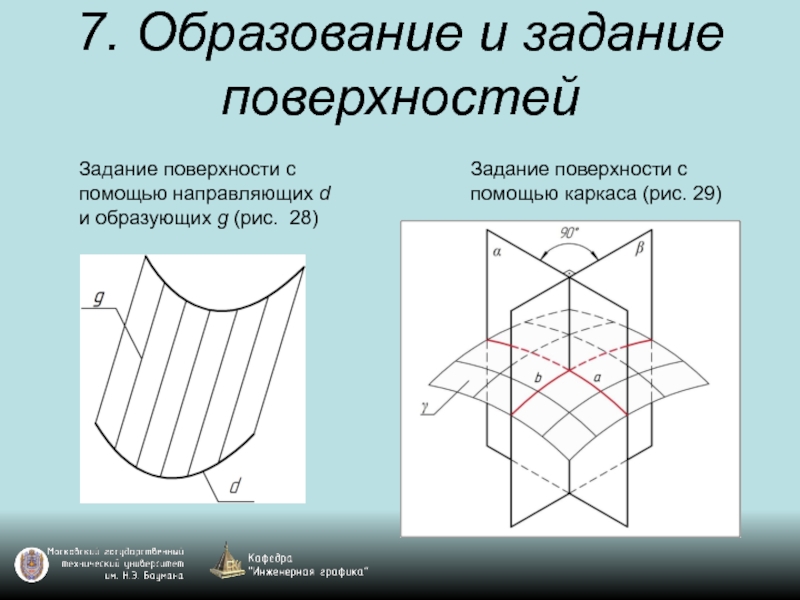
Слайд 397. Образование и задание поверхностей
Задание поверхности с помощью каркаса (рис. 29)
Задание
поверхности с помощью направляющих d и образующих g (рис. 28)
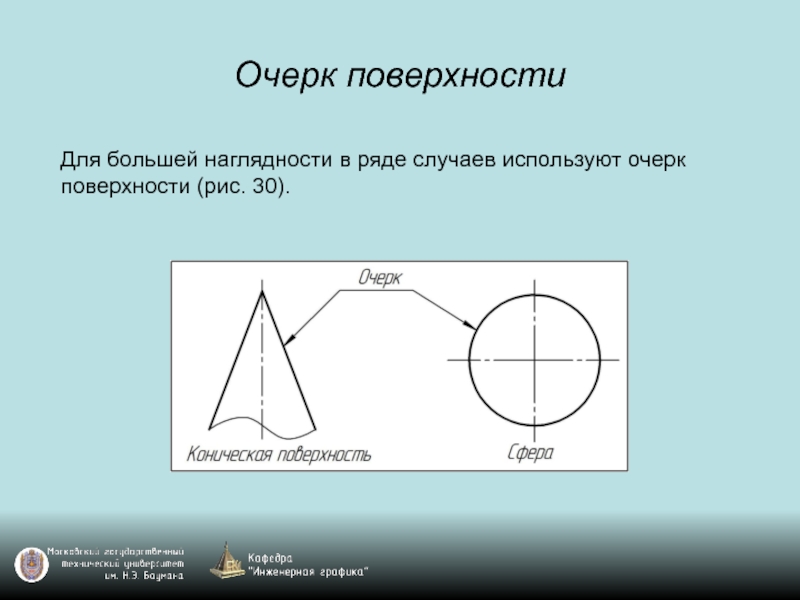
Слайд 40Очерк поверхности
Для большей наглядности в ряде случаев используют очерк поверхности (рис.
30).
Слайд 41Общее правило построения проекции точки, принадлежащей поверхности:
Для построения проекции точки, принадлежащей
поверхности, надо воспользоваться проекциями линии, принадлежащей поверхности и проходящей через заданную точку.
Слайд 42Обзор поверхностей
Можно группировать поверхности:
по форме образующей: линейчатые, нелинейчатые;
по движению образующей: параллельный
перенос, вращение, винтовое;
по возможности развернуть на плоскость: развертываемые, неразвертываемые.
по возможности развернуть на плоскость: развертываемые, неразвертываемые.
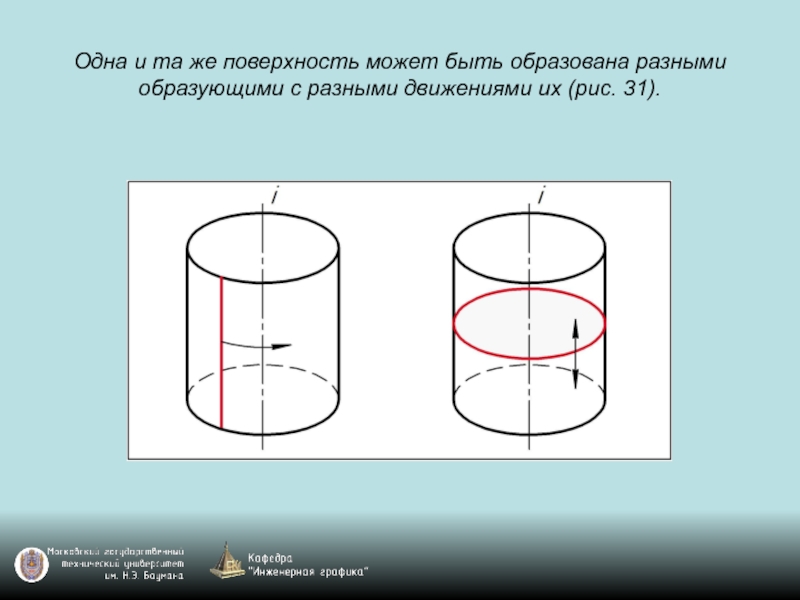
Слайд 43Одна и та же поверхность может быть образована разными образующими с
разными движениями их (рис. 31).
Слайд 44Одна и та же поверхность может быть образована разными образующими с
разными движениями их (рис. 31).
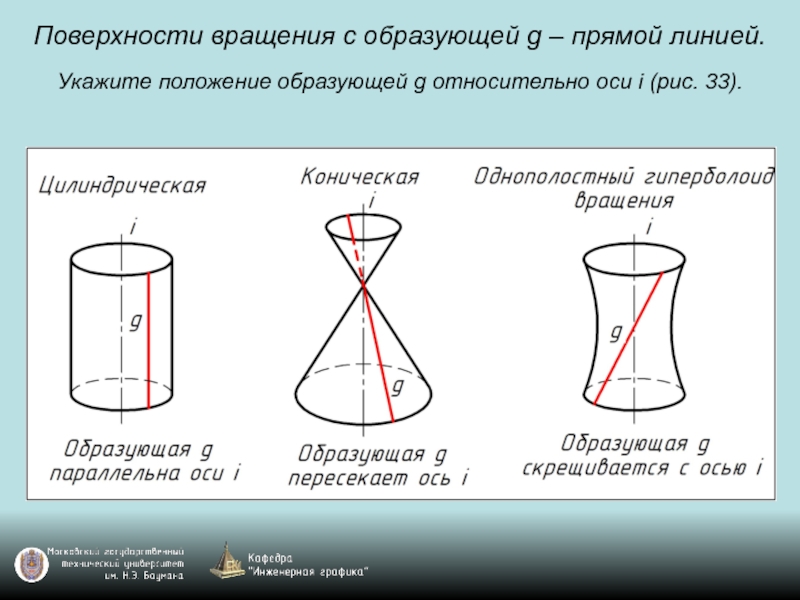
Слайд 65Поверхности вращения с образующей g – прямой линией. Укажите положение образующей g
относительно оси i (рис. 33).
Слайд 66Поверхности вращения с образующей g – прямой линией. Укажите положение образующей g
относительно оси i (рис. 33).
Слайд 67Поверхности вращения с образующей g – прямой линией. Укажите положение образующей g
относительно оси i (рис. 33).
Слайд 68Поверхности вращения с образующей g – прямой линией. Укажите положение образующей g
относительно оси i (рис. 33).
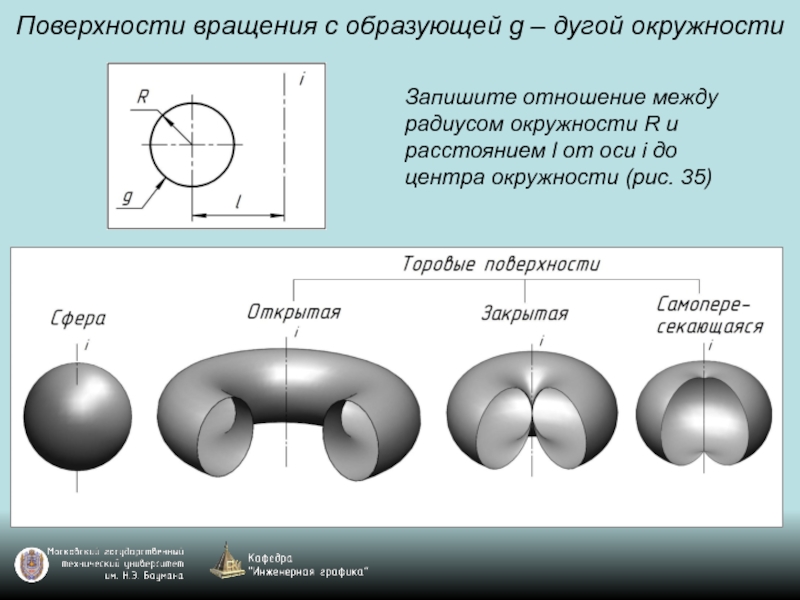
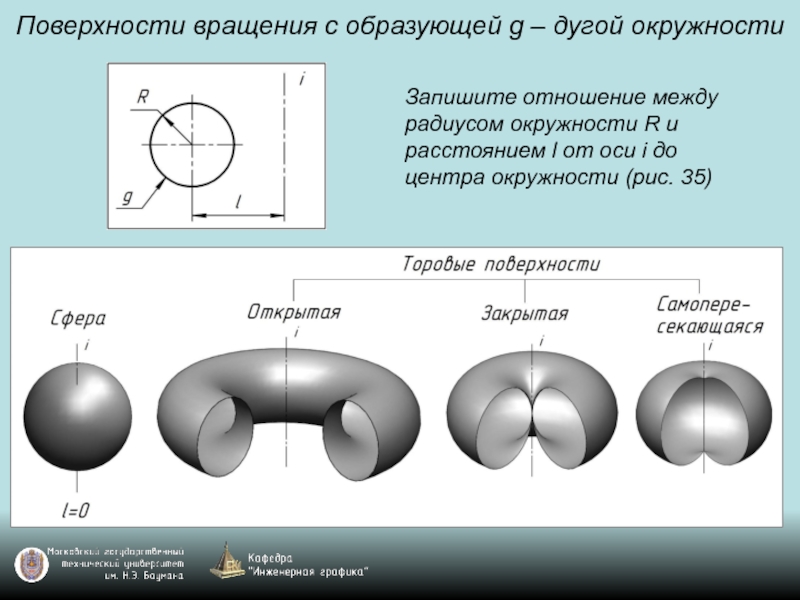
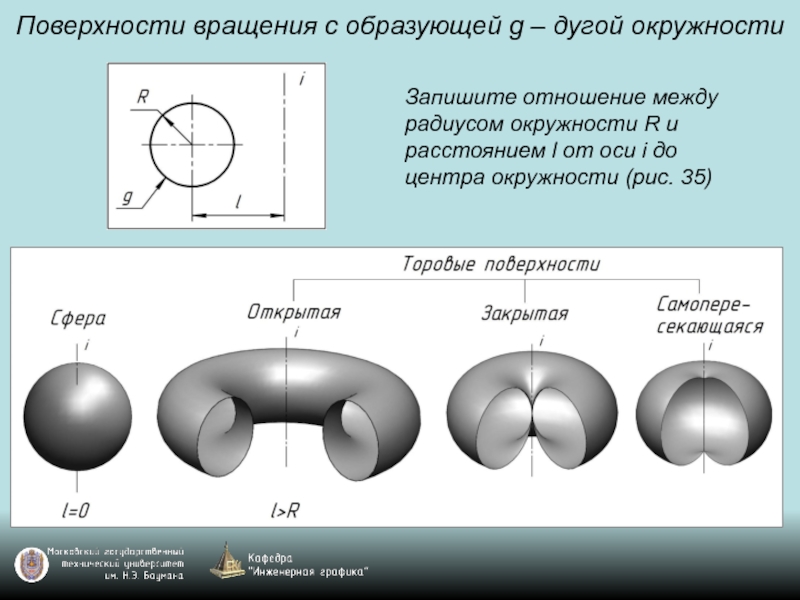
Слайд 89Поверхности вращения с образующей g – дугой окружности
Запишите отношение между радиусом
окружности R и расстоянием l от оси i до центра окружности (рис. 35)
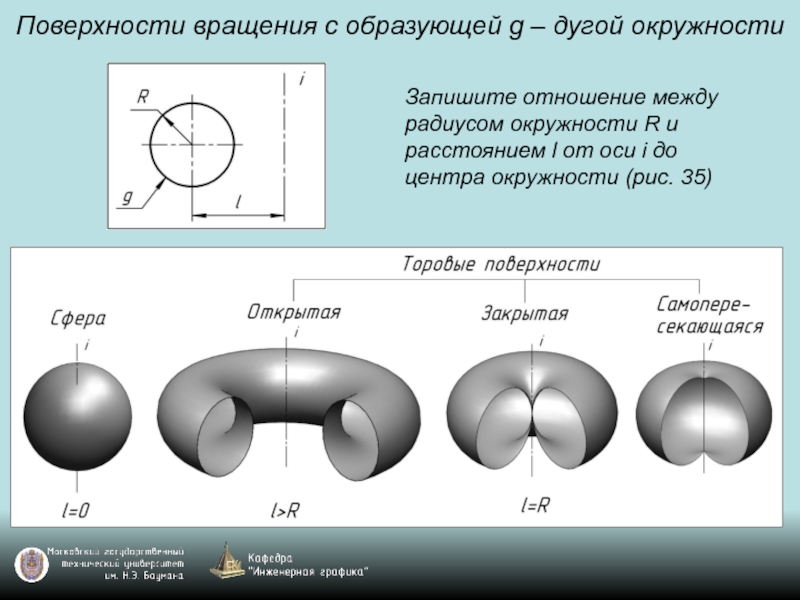
Слайд 90Поверхности вращения с образующей g – дугой окружности
Запишите отношение между радиусом
окружности R и расстоянием l от оси i до центра окружности (рис. 35)
Слайд 91Поверхности вращения с образующей g – дугой окружности
Запишите отношение между радиусом
окружности R и расстоянием l от оси i до центра окружности (рис. 35)
Слайд 92Поверхности вращения с образующей g – дугой окружности
Запишите отношение между радиусом
окружности R и расстоянием l от оси i до центра окружности (рис. 35)
Слайд 93Поверхности вращения с образующей g – дугой окружности
Запишите отношение между радиусом
окружности R и расстоянием l от оси i до центра окружности (рис. 35)
Слайд 117Винтовые поверхности
Винтовая поверхность образована винтовым движением образующей, т.е.
вращением образующей вокруг оси и одновременным перемещением вдоль оси i.
Все точки образующей gi перемещаются по винтовым линиям. Винтовая линия является направляющей d винтовой поверхности.
Ход винтовой поверхности Ph.– величина линейного перемещения точки винтовой поверхности при повороте этой точки на угол 360° вокруг оси поверхности. Ход винтовой поверхности определяется ходом винтовой линии
Винтовые поверхности различают в зависимости от параметров винтовой линии и формы образующей.
Все точки образующей gi перемещаются по винтовым линиям. Винтовая линия является направляющей d винтовой поверхности.
Ход винтовой поверхности Ph.– величина линейного перемещения точки винтовой поверхности при повороте этой точки на угол 360° вокруг оси поверхности. Ход винтовой поверхности определяется ходом винтовой линии
Винтовые поверхности различают в зависимости от параметров винтовой линии и формы образующей.
Слайд 118Чаще всего в технике применяют в качестве направляющей цилиндрическую винтовую линию,
называемую гелисой. Винтовая поверхность с прямолинейной образующей (линейчатая винтовая поверхность) с направляющей гелисой называется геликоидом.
Геликоиды разделяются на закрытые (g∩i), открытые (g ∙ i), прямые (g ┴ i), наклонные (g не ┴ i).
Геликоиды разделяются на закрытые (g∩i), открытые (g ∙ i), прямые (g ┴ i), наклонные (g не ┴ i).