Кригинг презентация

(Среднее значение и Дисперсия).
Предположение :
Стационарность
Среднее значение не должно меняться по латерали
Отсутствие трендов
Входные данные:
Набор значений
Вариограмма и функция распределения
Использование и ограничения:
Поиск тренда и визуализация трендов
Сглаженный и точный результат
Плохо работает с экстремально высокими значениями

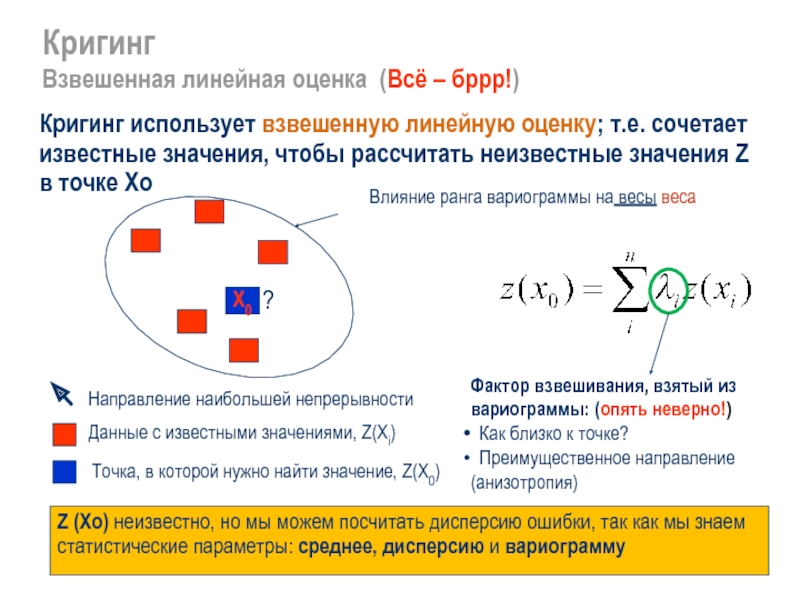
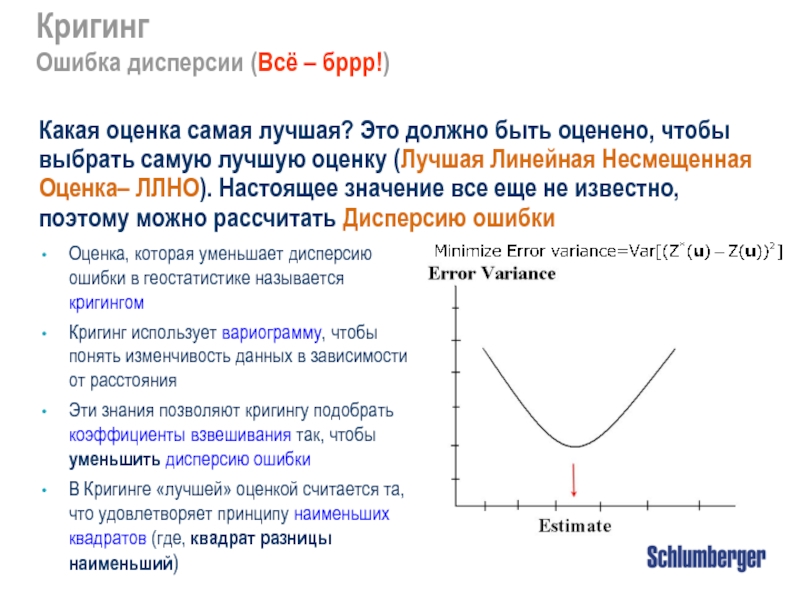
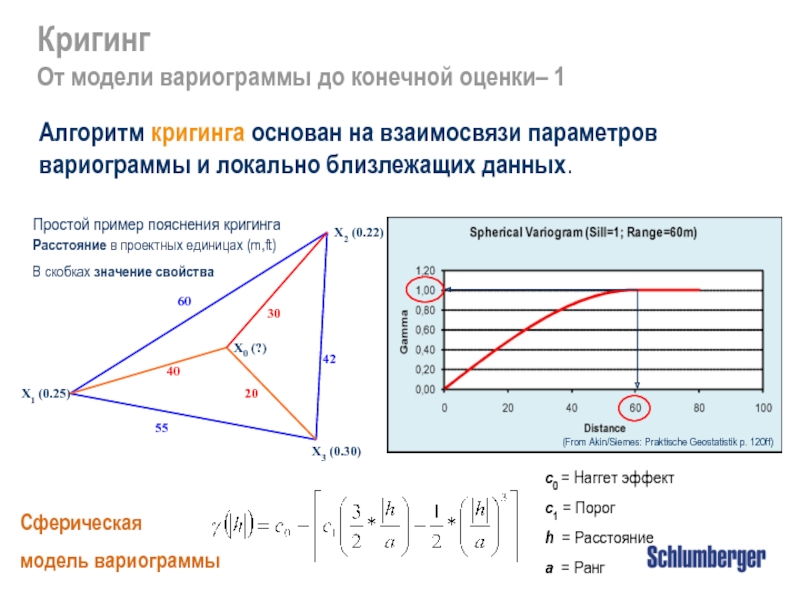
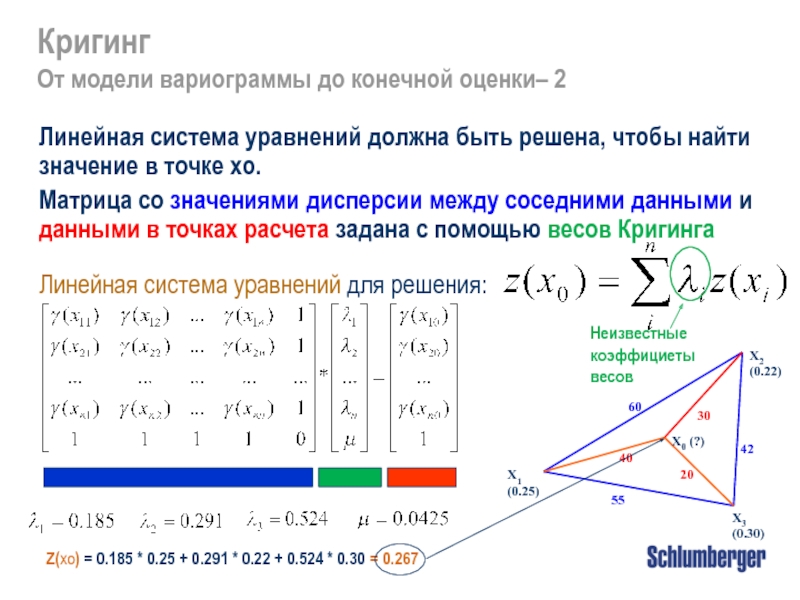
Кригинг Принципы

вычисляются по модели вариограммы (неверно – как решения нормальной системы, в которой коэфициенты “вычисляются по модели вариограммы”)
Известные значения z(xi),например, скважинные данные

Пример:
На 2D поверхности или 3D гриде известная значения (например, пористость) – это скважины. Все другие ячейки грида должны быть рассчитаны:

можем посчитать дисперсию ошибки, так как мы знаем статистические параметры: среднее, дисперсию и вариограмму

Кригинг использует взвешенную линейную оценку; т.е. сочетает известные значения, чтобы рассчитать неизвестные значения Z в точке Xo

Фактор взвешивания, взятый из
вариограммы: (опять неверно!)
Как близко к точке?
Преимущественное направление
(анизотропия)

Влияние ранга вариограммы на весы веса

геостатистике называется кригингом
Кригинг использует вариограмму, чтобы понять изменчивость данных в зависимости от расстояния
Эти знания позволяют кригингу подобрать коэффициенты взвешивания так, чтобы уменьшить дисперсию ошибки
В Кригинге «лучшей» оценкой считается та, что удовлетворяет принципу наименьших квадратов (где, квадрат разницы наименьший)

Какая оценка самая лучшая? Это должно быть оценено, чтобы выбрать самую лучшую оценку (Лучшая Линейная Несмещенная Оценка– ЛЛНО). Настоящее значение все еще не известно, поэтому можно рассчитать Дисперсию ошибки

может быть меньше, чем 1
Чем меньше весовые коэффициенты, тем большее влияние математического ожидания m на вычисленное значение Z в точке x0
Глобальное среднее используется кригинг алгоритмом для расчета весовых коэффициентов. И среднее значение предполагается известным
По умолчанию в Petrel используется этот кригинг алгоритм

Kригинг Tипы (Всё – бррр!)

ВСЕГДА равна 1
Значение локального математического ожидания используется в кригинг алгоритме при расчете весовых параметров. Среднее предполагается равное константе, но неизвестно

Kригинг Tипы

вариограммы

(From Akin/Siemes: Praktische Geostatistik p. 120ff)

Кригинг От модели вариограммы до конечной оценки– 1

Простой пример пояснения кригинга Расстояние в проектных единицах (m,ft)
В скобках значение свойства

Алгоритм кригинга основан на взаимосвязи параметров вариограммы и локально близлежащих данных.

Линейная система уравнений для решения:

Кригинг От модели вариограммы до конечной оценки– 2

Неизвестные
коэффициеты
весов

Линейная система уравнений должна быть решена, чтобы найти значение в точке xo.
Матрица со значениями дисперсии между соседними данными и данными в точках расчета задана с помощью весов Кригинга

Z(xo) = 0.185 * 0.25 + 0.291 * 0.22 + 0.524 * 0.30 = 0.267

5000м

Хорошо

Плохо

Кригинг Влияние параметров модели ваиограммы

Азимут (сферическая вариограмма)

5000m
Наггет: 0.99

Анизотропия: -45 градусов
Ранг : 10000m / 5000m
Наггет : 0.1

только внутри ранга вариограммы.
Кригинг Gsilb
Есть Collocated co-kriging и экспертные настройки,
но производительность ниже, чем у кригинга.
Кригинг
Работает с большим количеством данных, комбинируя многопоточность и алгоритмы умного поиска. Включает параллелизацию, быстрый алгоритм Collocated co-kriging и экспертные настройки.

Предпочтителен