- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Координаты вектора презентация
Содержание
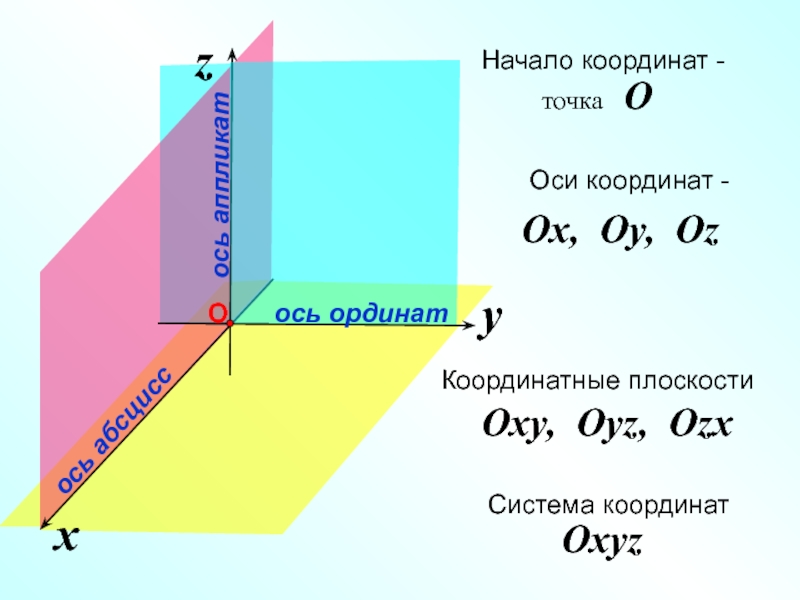
- 1. Координаты вектора
- 3. x
- 4. x z
- 5. y x z O (0;
- 7. В координатной плоскости Oxy
- 8. z A (4;-2,5; 7) S
- 9. y x z I
- 10. Вектор, начало которого совпадает с началом координат
- 11. y x z I
- 12. O (0; 0; 0) y x
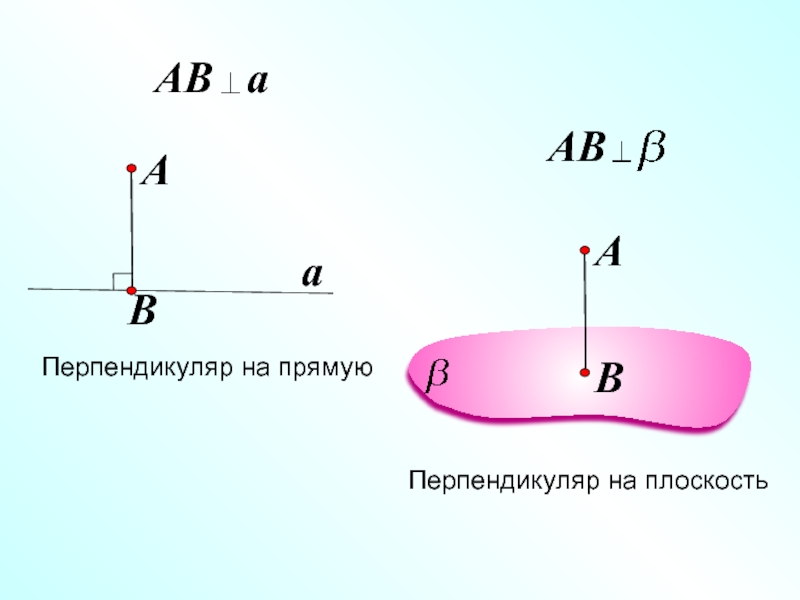
- 13. A A a Перпендикуляр на прямую Перпендикуляр на плоскость
- 14. x z
- 15. x z
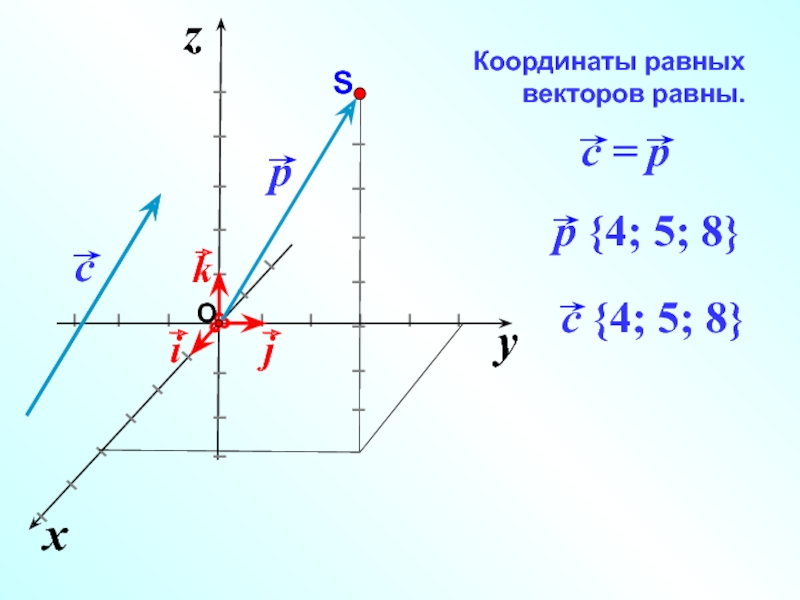
- 16. Координаты равных векторов равны. y x
- 17. 2) Напишите разложение вектора ОЕ
- 18. x z
- 19. a {-6; 9; 5} n {-8;
- 20. a {-6; 9; 5} n {-8;
- 21. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. 10
- 22. № 407 Даны векторы d {-2,7; 3,1; 0,5}
- 23. Каждая координата разности двух векторов равна разности
- 24. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. 30
- 25. 1 способ 2 способ
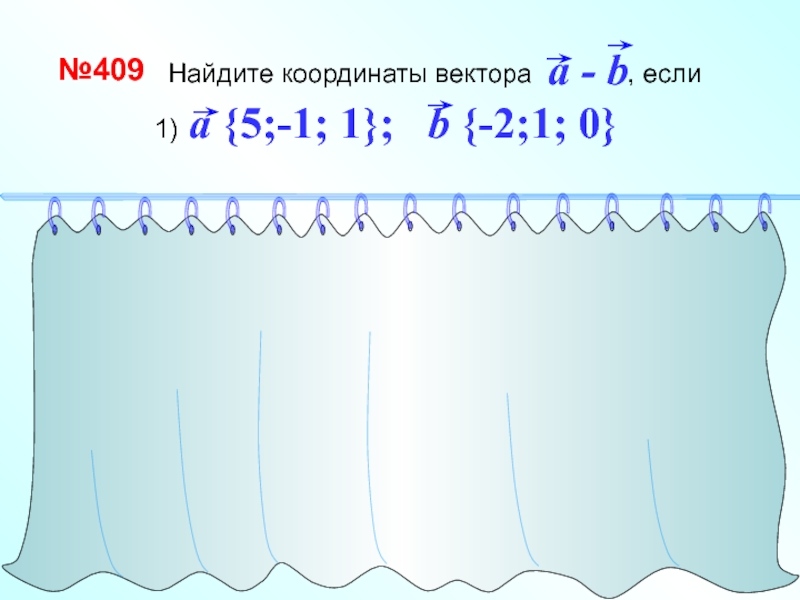
- 26. Найдите координаты вектора , если №409
- 27. + Даны векторы
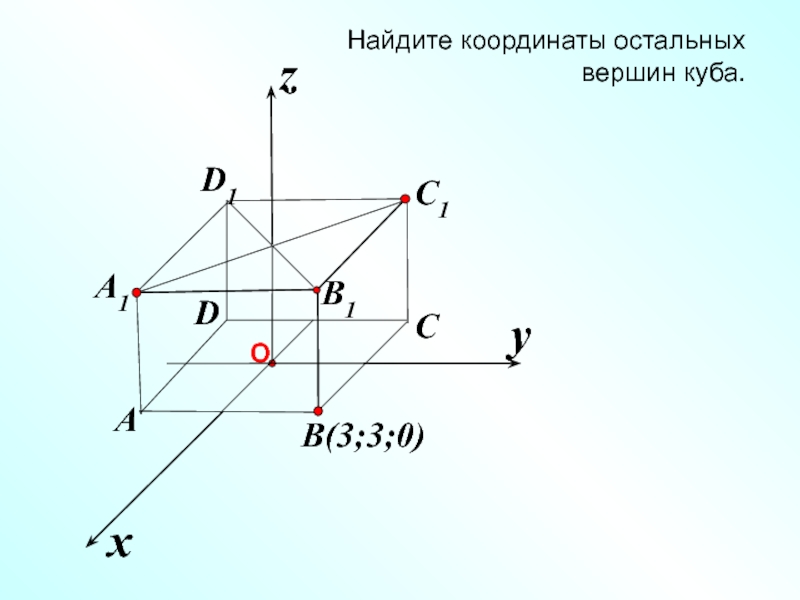
- 28. x z Найдите координаты остальных
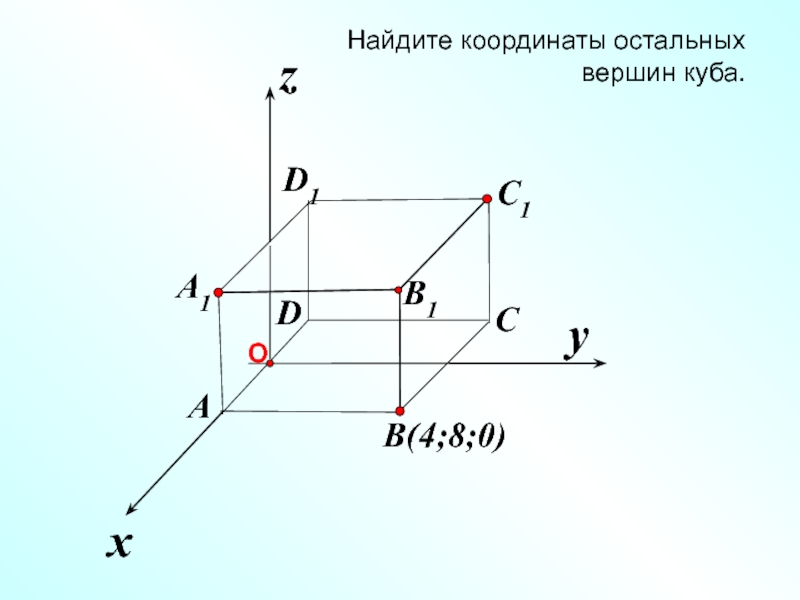
- 29. x z Найдите координаты остальных
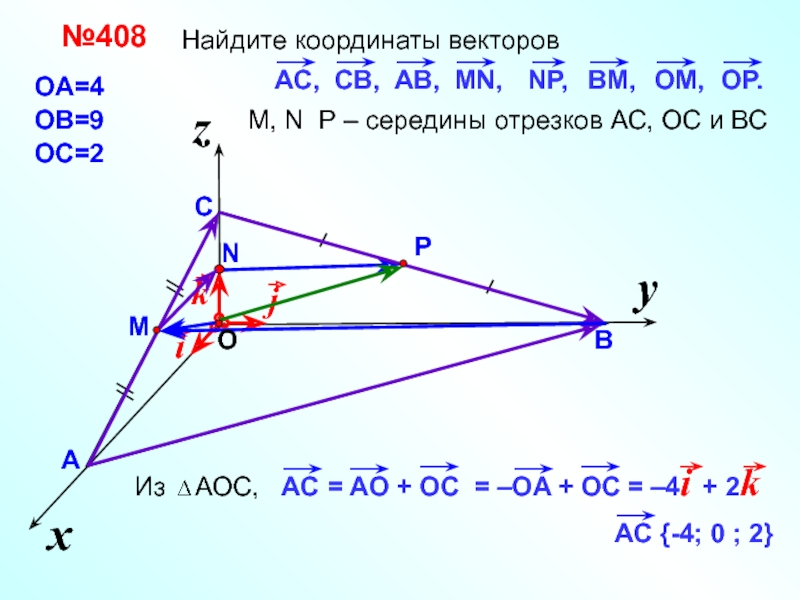
- 30. Найдите координаты векторов y x
Слайд 3
x
z
y
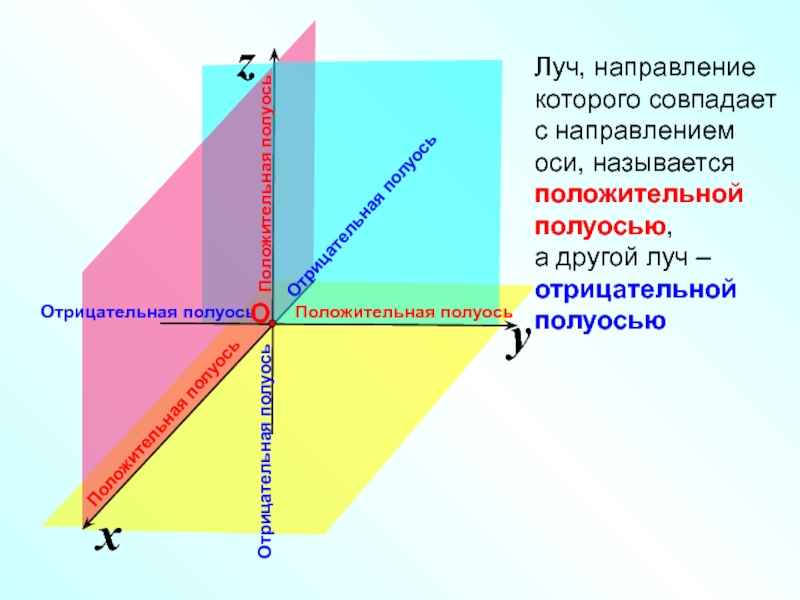
Луч, направление которого совпадает с направлением оси, называется положительной полуосью,
а
Слайд 4
x
z
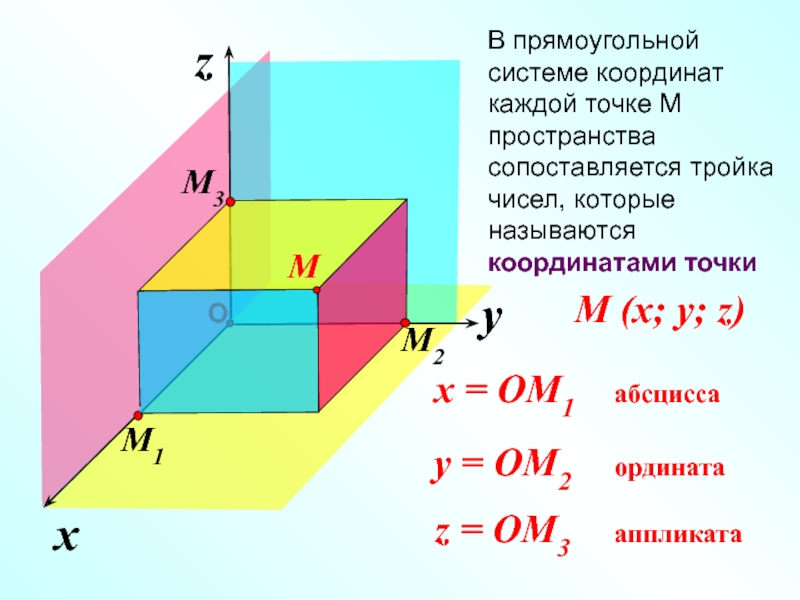
В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел,
y
M (x; y; z)
M
Слайд 5y
x
z
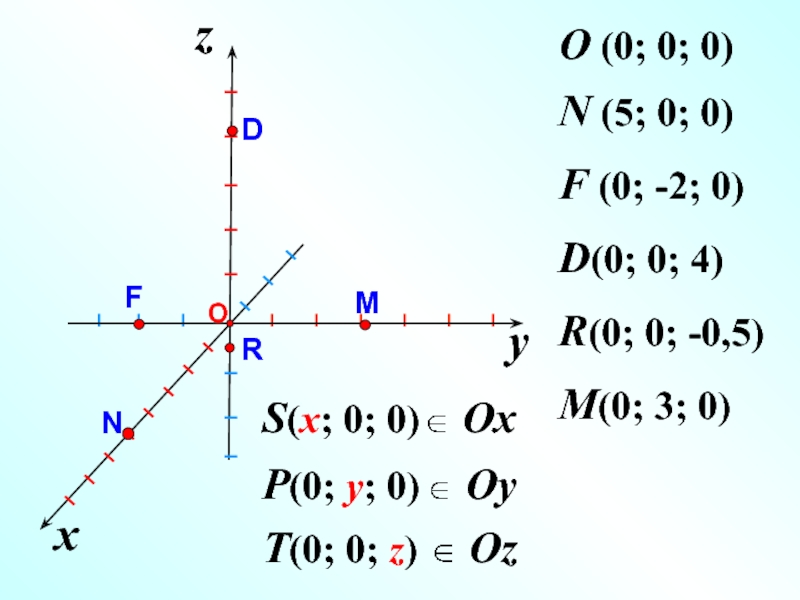
O (0; 0; 0)
N (5; 0; 0)
I I
I I I I I I I I I I I
F (0; -2; 0)
D(0; 0; 4)
R(0; 0; -0,5)
M(0; 3; 0)
S(x; 0; 0)
P(0; y; 0)
T(0; 0; z)
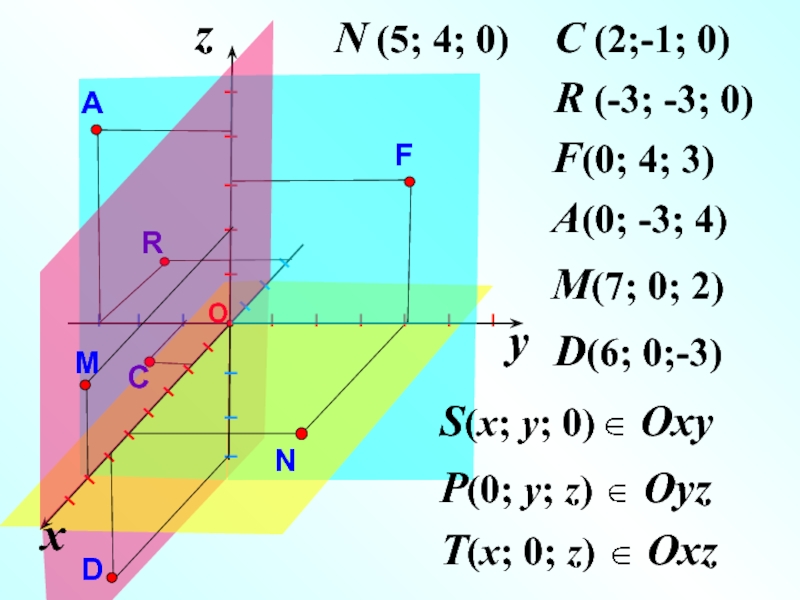
Слайд 6
z
N (5; 4; 0)
C (2;-1; 0)
I I
R (-3; -3; 0)
F(0; 4; 3)
A(0; -3; 4)
M(7; 0; 2)
S(x; y; 0)
P(0; y; z)
T(x; 0; z)
y
I I I I I I I I
x
D(6; 0;-3)
Слайд 7
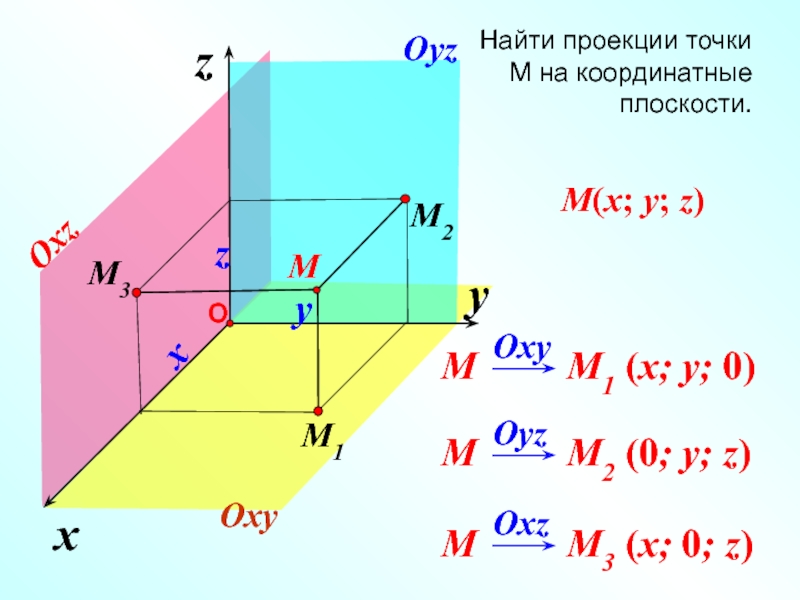
В координатной плоскости
Oxy (x; y; 0)
Oyz (0; y; z)
Oxz (x;
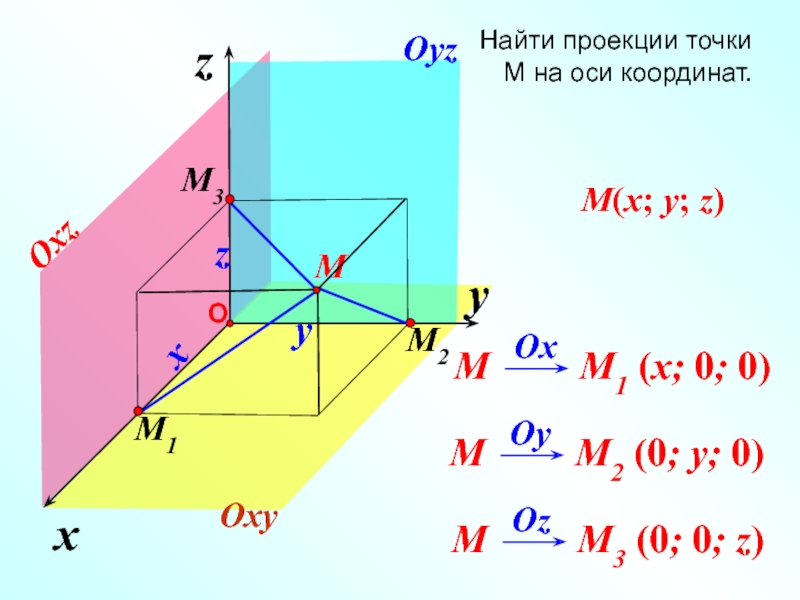
Ox (x; 0; 0)
Oy (0; y; 0)
Oz (0; 0; z)
На оси
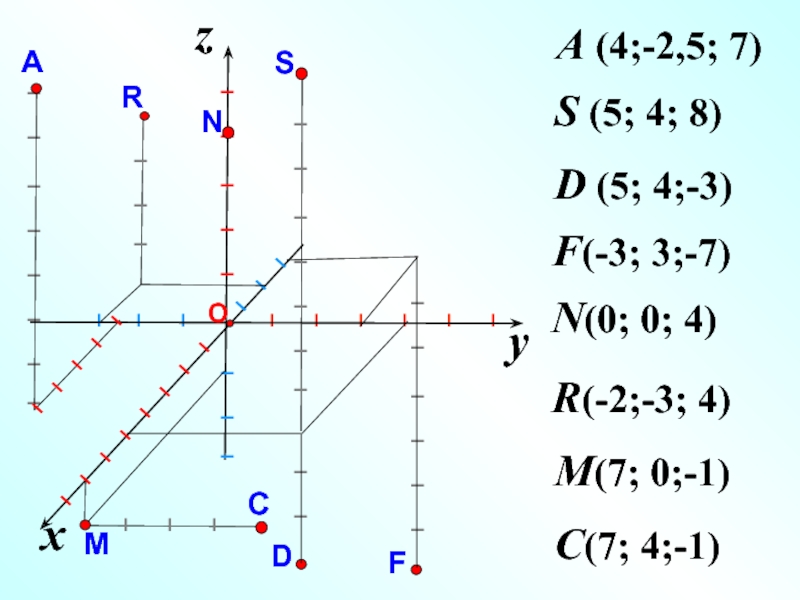
Слайд 8
z
A (4;-2,5; 7)
S (5; 4; 8)
I I
D (5; 4;-3)
F(-3; 3;-7)
N(0; 0; 4)
R(-2;-3; 4)
y
I I I I I I I I I
I I I I I I I I
x
M(7; 0;-1)
C(7; 4;-1)
Слайд 9y
x
z
I I I
I I I I I I I I
I I I I I I I I
разложение вектора по координатным векторам
F(x; y; z)
O
Координатные векторы не компланарны. Поэтому любой вектор можно разложить по координатным векторам, т.е. представить в виде
причем коэффициенты разложения определяются единственным образом.
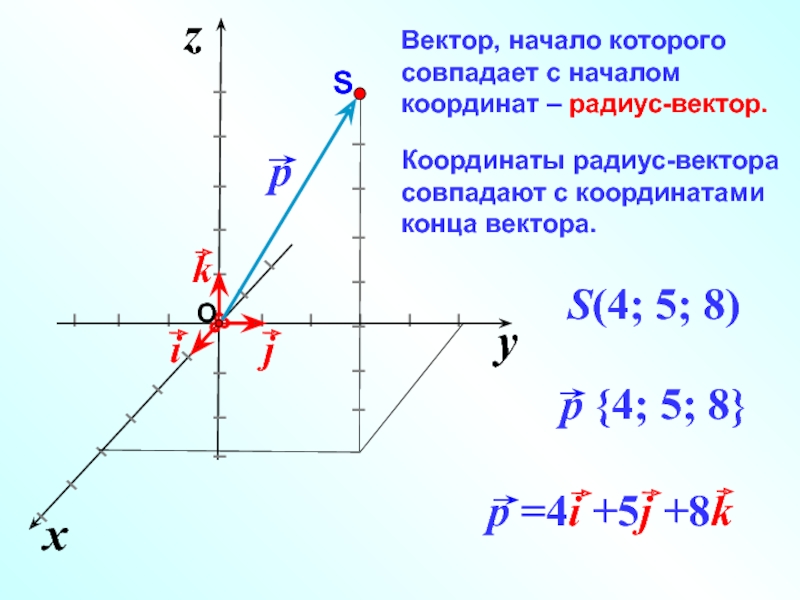
Слайд 10Вектор, начало которого совпадает с началом координат – радиус-вектор.
Координаты радиус-вектора совпадают
y
x
z
I I I I I I I I
I I I I I I I I
I I I I I I I I
S(4; 5; 8)
O
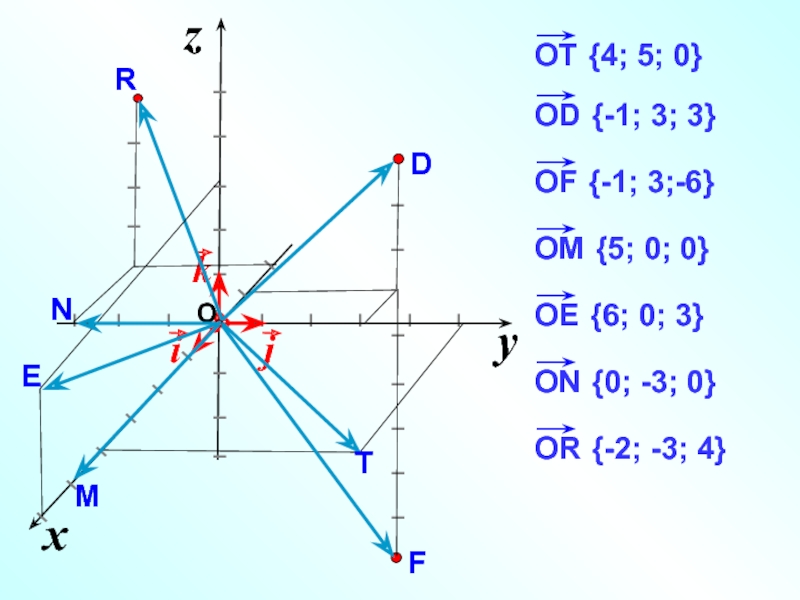
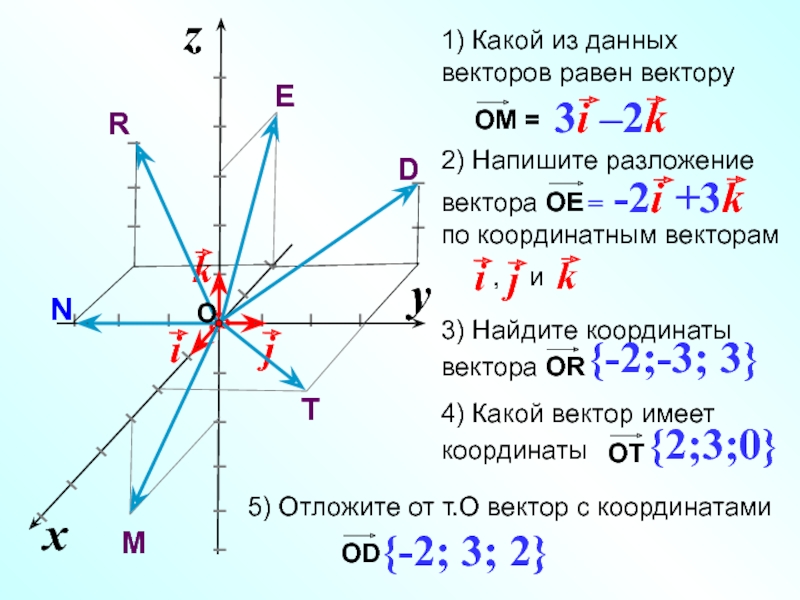
Слайд 172) Напишите разложение
вектора ОЕ
по координатным векторам
,
5) Отложите от т.О вектор с координатами
{-2; 3; 2}
{-2;-3; 3}
y
x
z
I I I I I I
I I I I I I I I I I
I I I I I I I I
I I I
R
I I
D
E
N
M
T
O
Слайд 18
x
z
АСВОА1С1В1О1 прямоугольный параллелепипед.
Найти координаты векторов
y
A
O1
B
C1
A1
B1
C
2
3
2
№ 405
OА1
{2; 0; 2}
OВ1
{0; 3; 2}
OО1
{0;
OС
{2; 3; 0}
OС1
{2; 3; 2}
ВС1
{2; 0; 2}
АС1
{0; 3; 2}
О1С
{2; 3; -2}
Слайд 21Каждая координата суммы двух или более векторов равна сумме соответствующих координат
10
Слайд 23Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
20
Слайд 24Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора
30