- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Координатные векторы презентация
Содержание
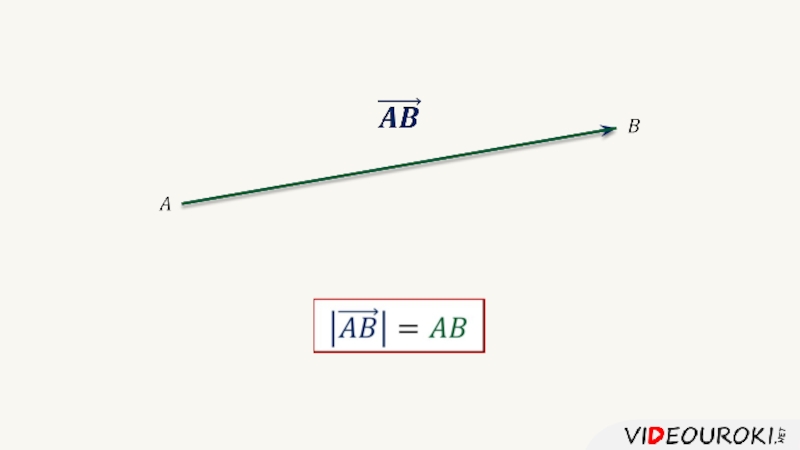
- 1. Координатные векторы
- 2.
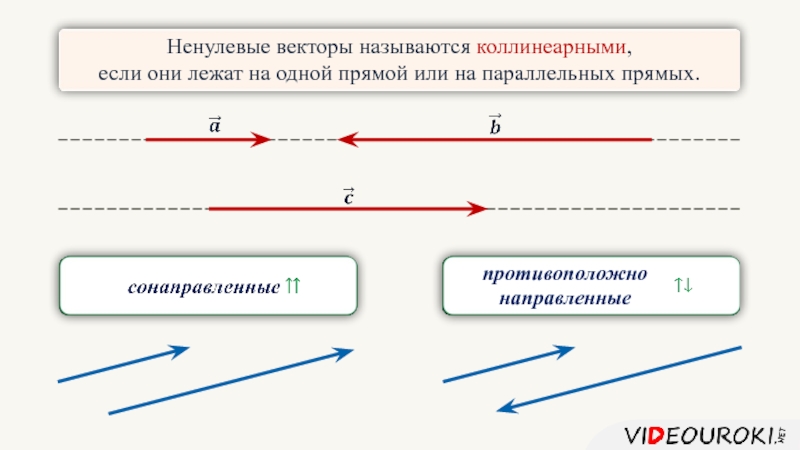
- 3. Ненулевые векторы называются коллинеарными, если они
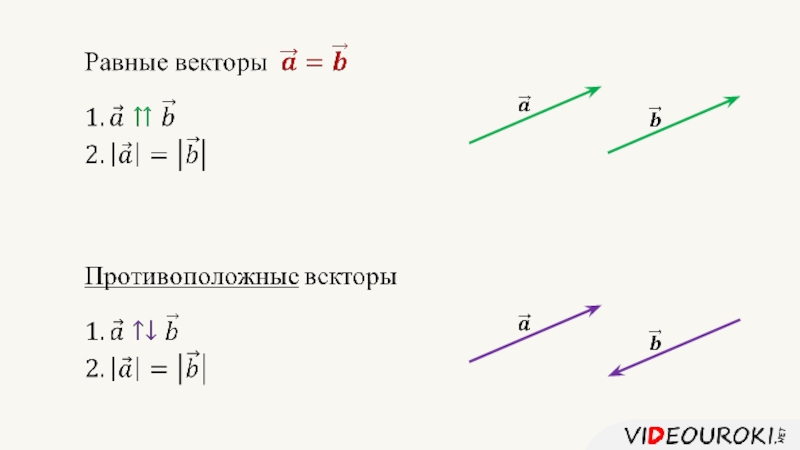
- 4.
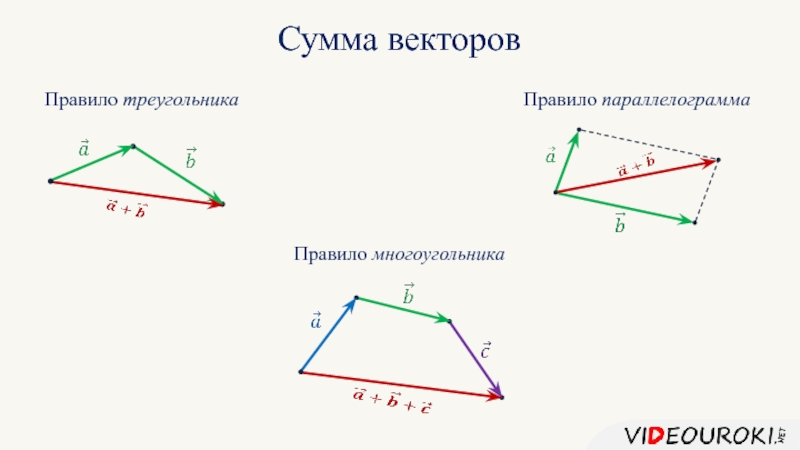
- 5. Сумма векторов
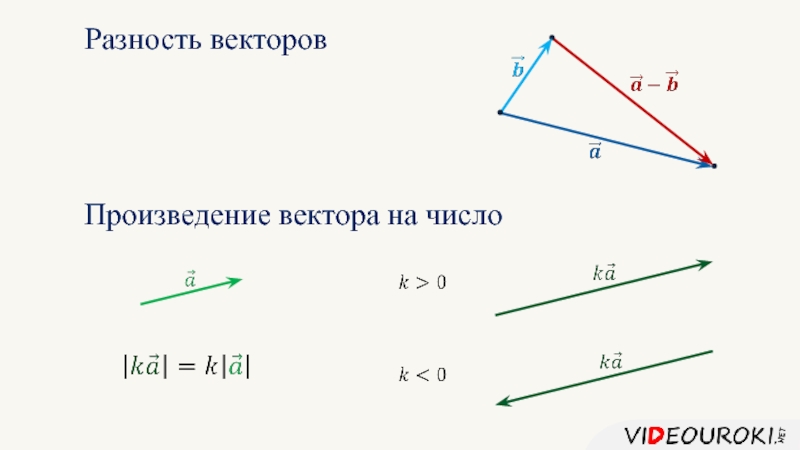
- 6. Разность векторов
- 7. Теорема. На плоскости
- 8.
- 9.
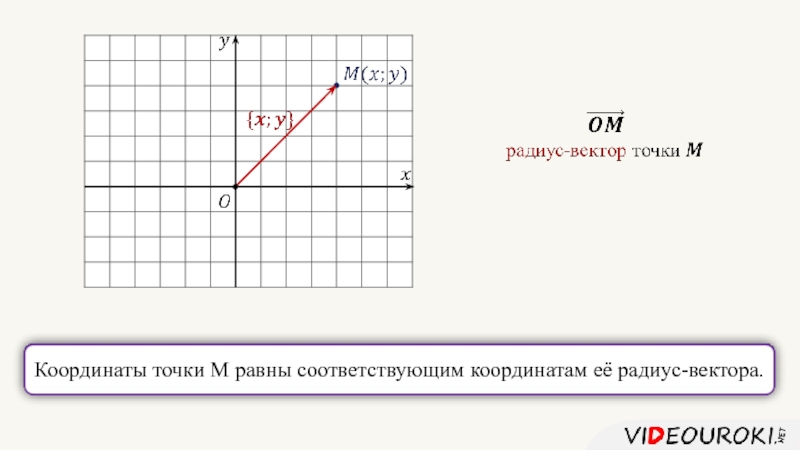
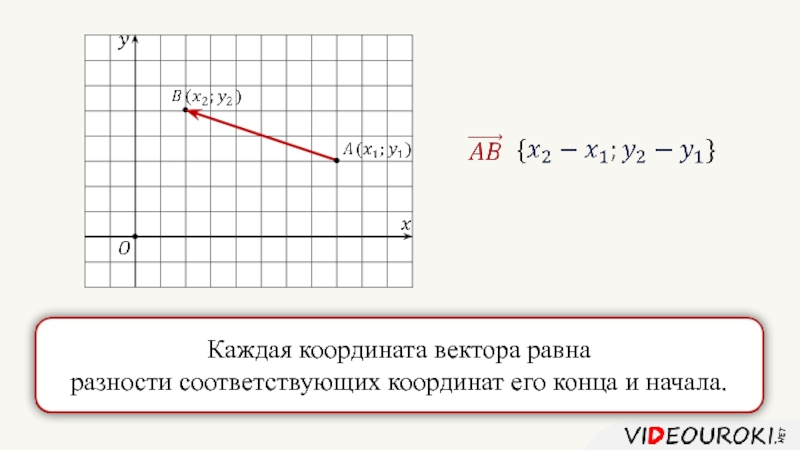
- 10. Координаты точки М равны соответствующим
- 11.
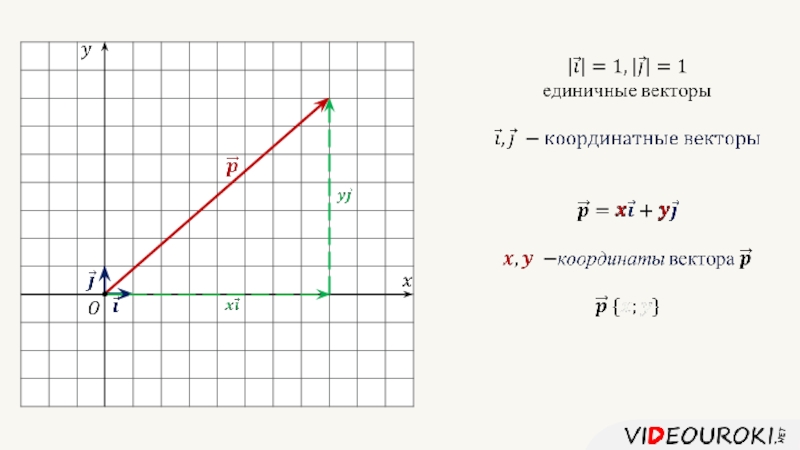
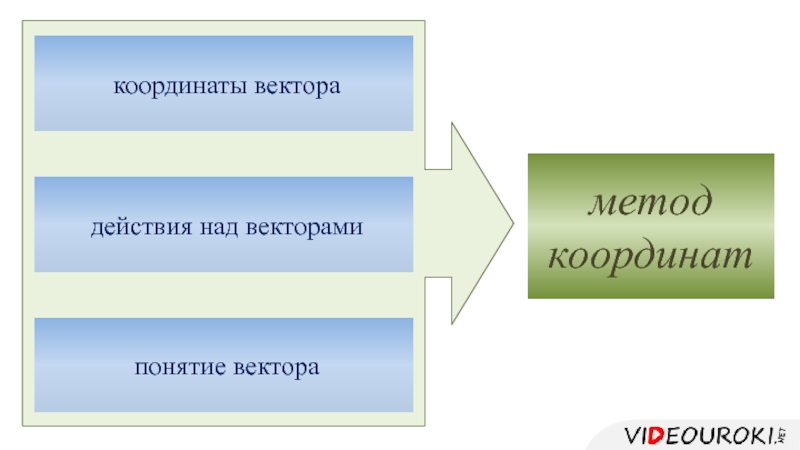
- 12. понятие вектора действия над векторами координаты вектора
- 13.
- 14. понятие вектора действия над векторами координаты вектора метод координат
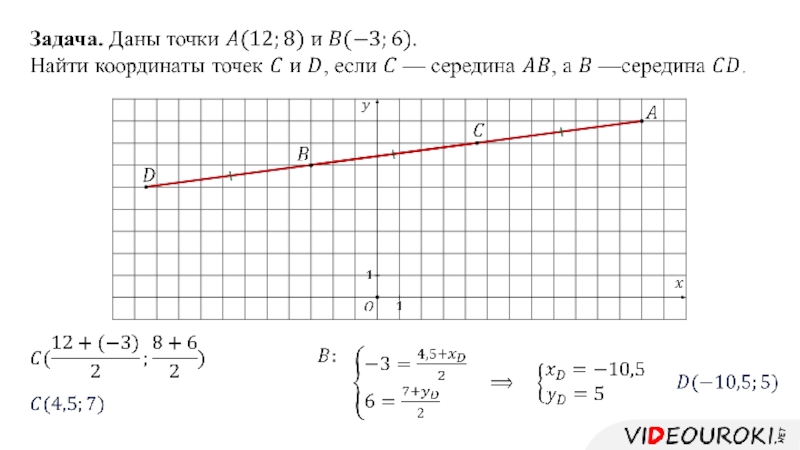
- 15. 1. Определение координат середины отрезка
- 17.
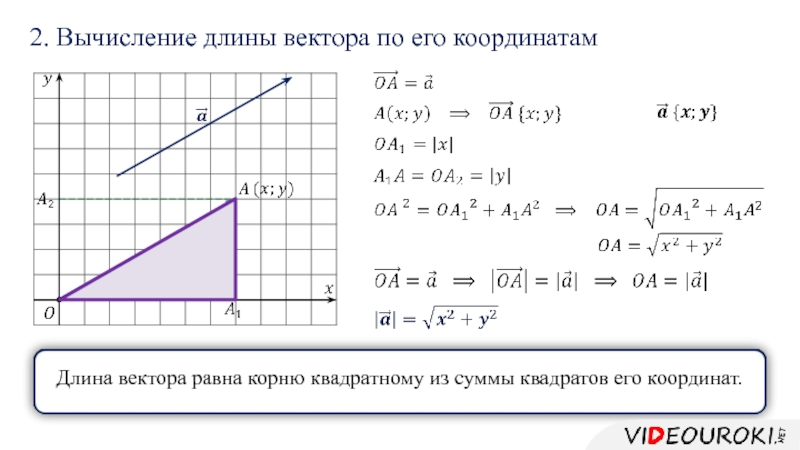
- 18. 2. Вычисление длины вектора по его координатам
- 19.
- 20.
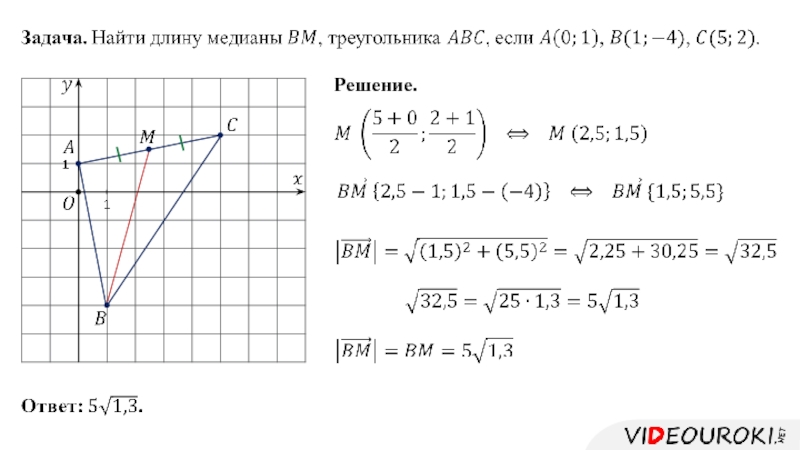
- 21. 3. Определение расстояния между двумя точками
- 22.
- 23.
Слайд 3
Ненулевые векторы называются коллинеарными,
если они лежат на одной прямой или на
параллельных прямых.
противоположно направленные
Слайд 7
Теорема. На плоскости любой вектор можно
разложить по двум данным неколлинеарным векторам,
причём
коэффициенты разложения определяются единственным образом.
Слайд 9
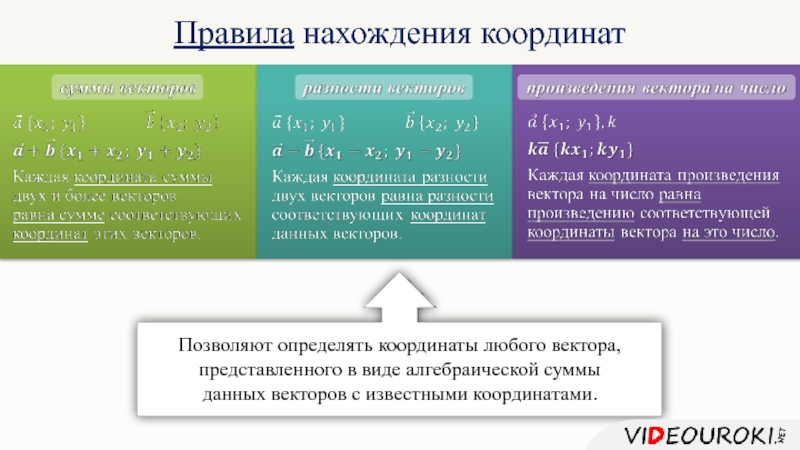
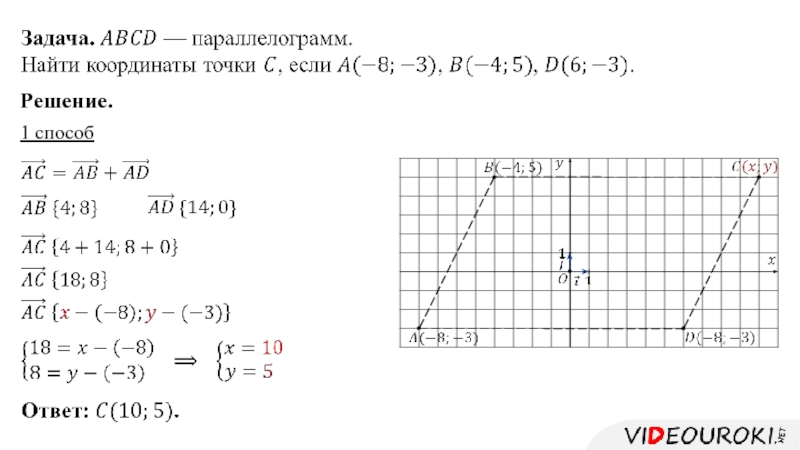
Правила нахождения координат
Позволяют определять координаты любого вектора,
представленного в виде алгебраической суммы
данных
векторов с известными координатами.
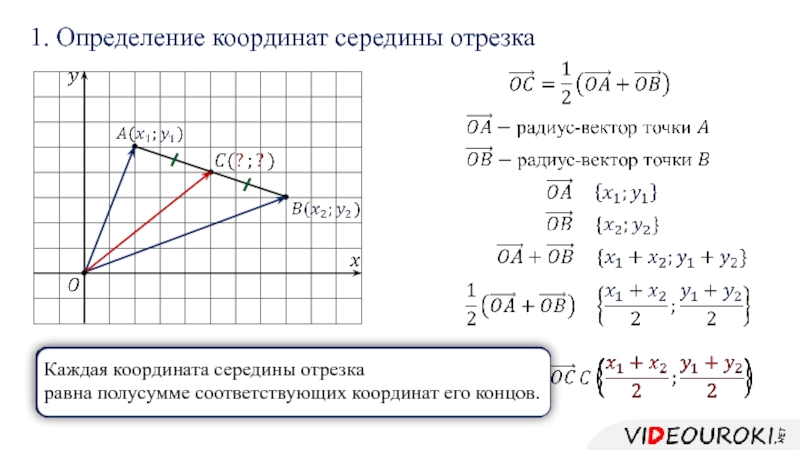
Слайд 151. Определение координат середины отрезка
Каждая координата середины отрезка
равна полусумме соответствующих координат
его концов.
Слайд 182. Вычисление длины вектора по его координатам
Длина вектора равна корню квадратному
из суммы квадратов его координат.