- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многогранники. Виды многогранников презентация
Содержание
- 1. Многогранники. Виды многогранников
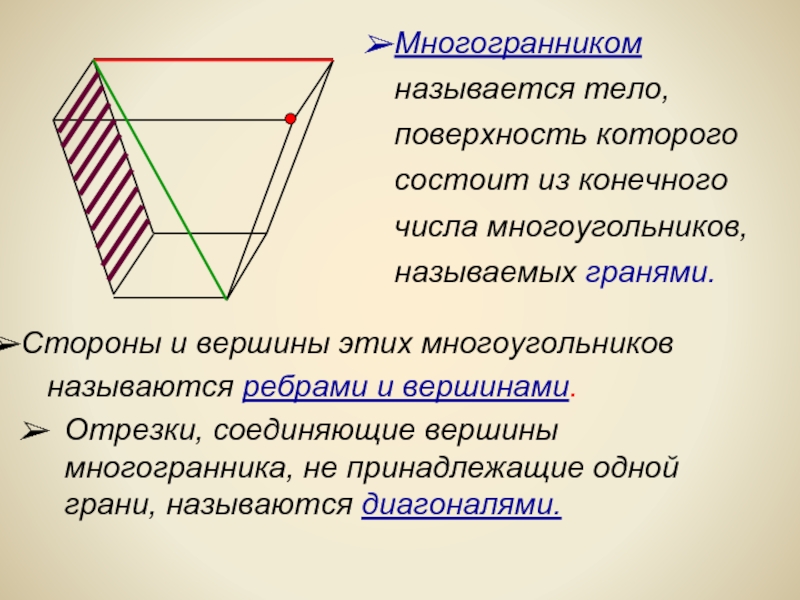
- 2. Отрезки, соединяющие вершины многогранника, не принадлежащие одной
- 3. Многогранник, поверхность которого состоит из двух
- 4. Многогранник, поверхность которого состоит из шести квадратов
- 5. Площадь призмы Sбок. + 2Sосн Sбок. =
- 6. Многогранник, поверхность которого состоит из многоугольника и
- 7. Основание правильный многоугольник, высота опущена в центр
- 8. Усеченная пирамида Боковые грани – трапеции
Слайд 2Отрезки, соединяющие вершины многогранника, не принадлежащие одной грани, называются диагоналями.
Многогранником
называется
поверхность которого
состоит из конечного
числа многоугольников,
называемых гранями.
Стороны и вершины этих многоугольников
называются ребрами и вершинами.
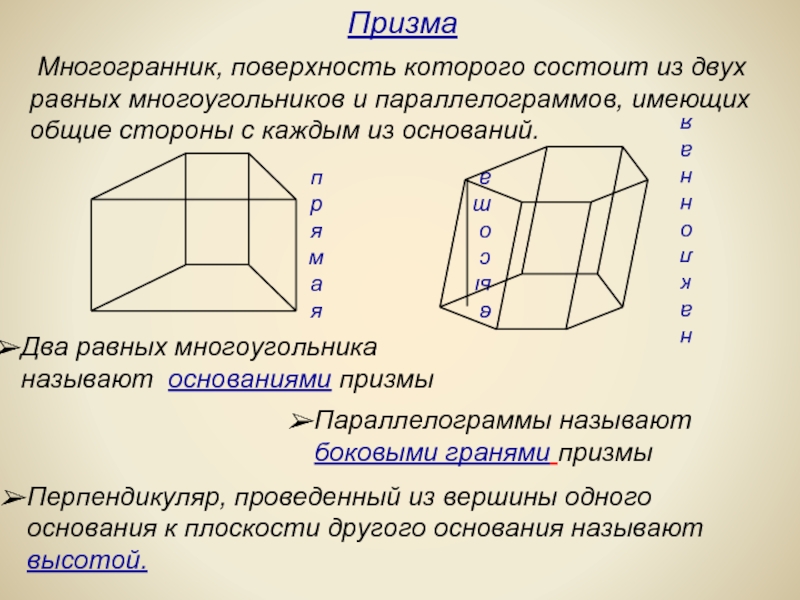
Слайд 3 Многогранник, поверхность которого состоит из двух равных многоугольников и параллелограммов,
вы
с
ота
п
р
я
м
а
я
н
а
к
л
о
н
н
а
я
Призма
Два равных многоугольника называют основаниями призмы
Параллелограммы называют
боковыми гранями призмы
Перпендикуляр, проведенный из вершины одного
основания к плоскости другого основания называют
высотой.
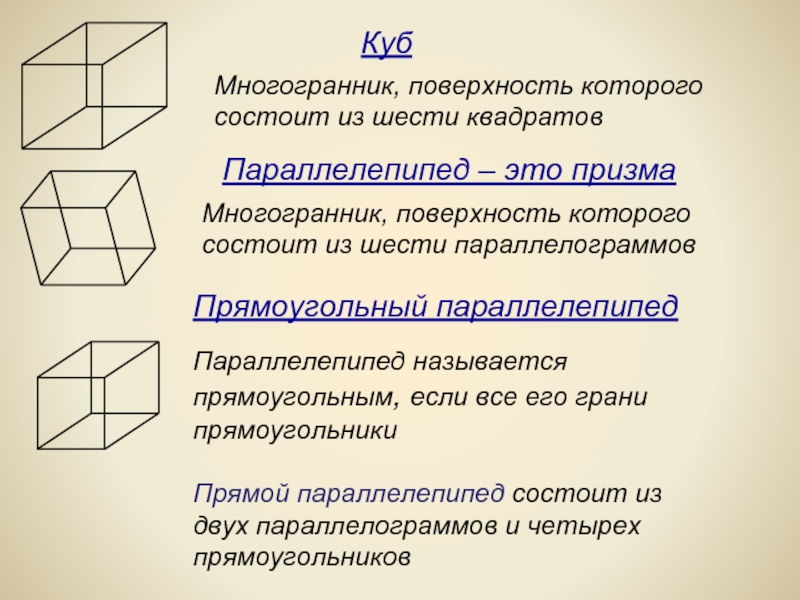
Слайд 4Многогранник, поверхность которого состоит из шести квадратов
Многогранник, поверхность которого
состоит из
Параллелепипед называется прямоугольным, если все его грани прямоугольники
Прямой параллелепипед состоит из двух параллелограммов и четырех прямоугольников
Куб
Прямоугольный параллелепипед
Параллелепипед – это призма
Слайд 5Площадь призмы
Sбок. + 2Sосн
Sбок. = Ph
a
b
h
Теорема: Площадь боковой поверхности прямой
призмы
на высоту.
Sполн. =
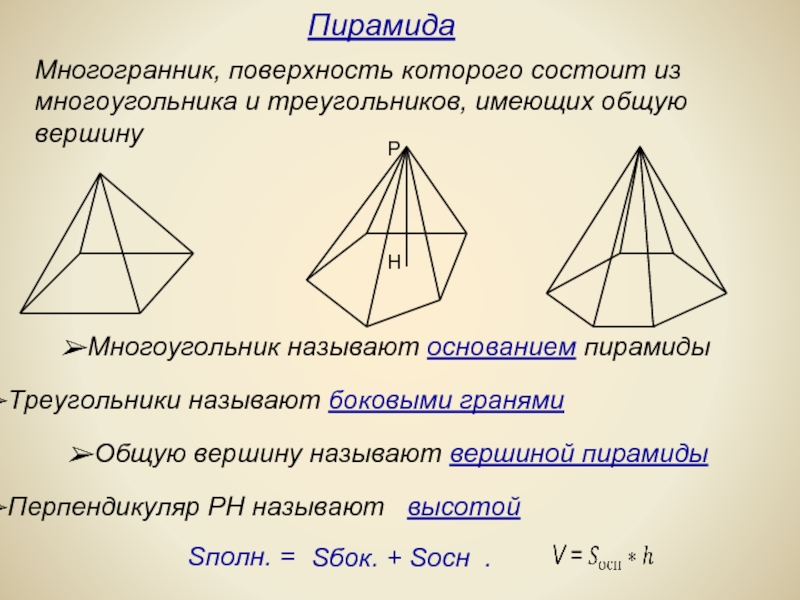
Слайд 6Многогранник, поверхность которого состоит из многоугольника и треугольников, имеющих общую вершину
Многоугольник
Треугольники называют боковыми гранями
Общую вершину называют вершиной пирамиды
Перпендикуляр РН называют высотой
Sбок. + Sосн .
Н
Р
Пирамида
Sполн. =
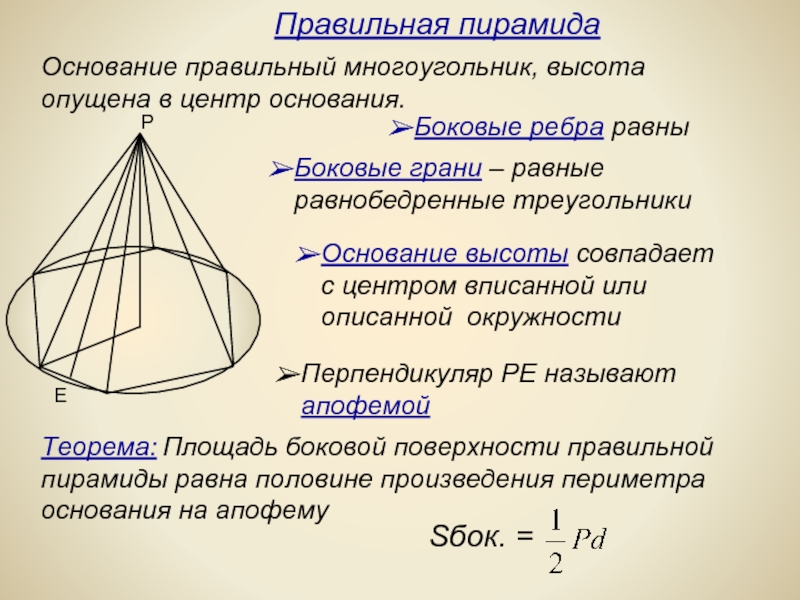
Слайд 7Основание правильный многоугольник, высота опущена в центр основания.
Перпендикуляр РЕ называют
Теорема: Площадь боковой поверхности правильной
пирамиды равна половине произведения периметра
основания на апофему
Р
Е
Правильная пирамида
Боковые ребра равны
Боковые грани – равные равнобедренные треугольники
Основание высоты совпадает
с центром вписанной или
описанной окружности
Слайд 8Усеченная пирамида
Боковые грани – трапеции
Теорема: Площадь боковой поверхности правильной
усеченной пирамиды
полусуммы периметров оснований на апофему