- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Контурный анализ презентация
Содержание
- 1. Контурный анализ
- 2. Взаимокорреляционная функция взаимокорреляционная функция (ВКФ) двух контуров
- 3. Взаимокорреляционная функция (2) Значения ВКФ показывают насколько
- 4. Взаимокорреляционная функция (3)
- 5. Автокорреляционная функция это скалярное произведение контура самого
- 6. Автокорреляционная функция (2) Свойства АКФ: не зависит
- 7. Автокорреляционная функция (3) АКФ контура можно считать
- 8. Практическое задание (ВКФ и АКФ)
- 9. Задача распознавания Последовательность действия при распознавании выглядит
- 10. Дескриптор контура Дескриптор – величина, характеризующая форму
- 11. Свертка АКФ АКФ - вектор с k/2
- 12. Особенности сравнения АКФ: Сравнение АКФ, в общем
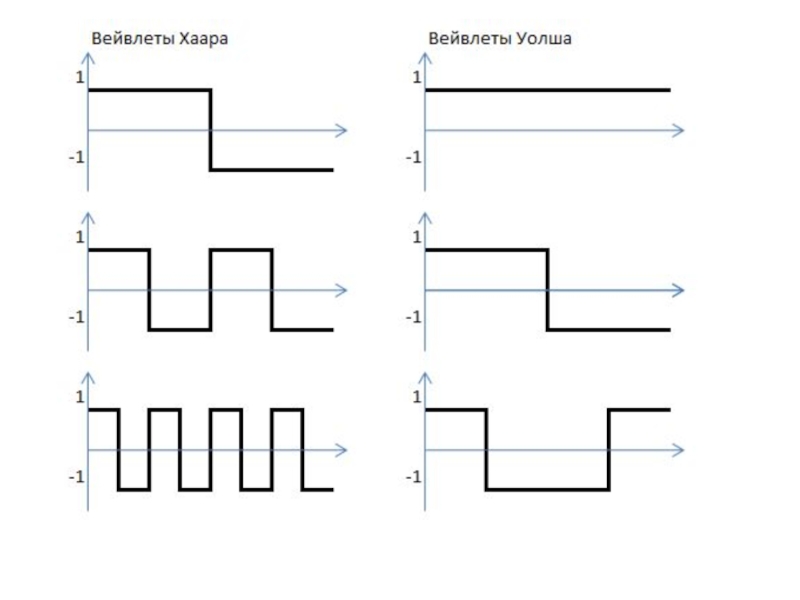
- 14. Практическое задание (вейвлет)
- 15. Эквализация контуров фиксируем длину ВК для каждого исходного контура Г создаем вектор-контур N длиной k
- 16. Эквализация контуров (2) Если исходный контур больше
- 17. Эквализация контуров (3) исходный контур меньше k,
- 18. Недостатки КА проблемой выделения контура на изображениях
- 19. Недостатки КА описывает весь объект целиком, и
- 20. Заключение Методы КА привлекательны своей простотой и
Слайд 2Взаимокорреляционная функция
взаимокорреляционная функция (ВКФ) двух контуров
Где N(m) — контур, полученный из
N путем циклического сдвига его ЭВ на m элементов.
Слайд 3Взаимокорреляционная функция (2)
Значения ВКФ показывают насколько похожи контуры Г и N,
если сдвинуть начальную точку N на m позиций.
ВКФ определена на всем множестве целых чисел.
ВКФ является периодической, с периодом k.
ВКФ определена на всем множестве целых чисел.
ВКФ является периодической, с периодом k.
Слайд 4Взаимокорреляционная функция (3)
τmax является мерой похожести двух контуров, инвариантной переносу, масштабированию,
вращению и сдвигу начальной точки.
arg(τmax) дает угол поворота одного контура, относительно другого.
arg(τmax) дает угол поворота одного контура, относительно другого.
Слайд 5Автокорреляционная функция
это скалярное произведение контура самого на себя при различных сдвигах
начальной точки:
Слайд 6Автокорреляционная функция (2)
Свойства АКФ:
не зависит от выбора начальной точки контура
Модуль АКФ
симметричен относительно центрального отсчета k/2
Если контур имеет какую-либо симметрию относительно поворота, то аналогичную симметрию имеет его АКФ
Если контур имеет какую-либо симметрию относительно поворота, то аналогичную симметрию имеет его АКФ
Слайд 7Автокорреляционная функция (3)
АКФ контура можно считать характеристикой формы контура.
Нормированная АКФ не
зависит от масштаба, положения, вращения и выбора начальной точки контура.
Слайд 9Задача распознавания
Последовательность действия при распознавании выглядит так:
Предварительная обработка изображения — сглаживание,
фильтрация помех, повышение контраста.
Бинаризация изображения и выделение контуров объектов.
Начальная фильтрация контуров по периметру, площади, коэффициенту формы, фрактальности и так далее.
Приведение контуров к единой длине, сглаживание.
Перебор всех найденных контуров, поиск шаблона, максимально похожего на данный контур.
Бинаризация изображения и выделение контуров объектов.
Начальная фильтрация контуров по периметру, площади, коэффициенту формы, фрактальности и так далее.
Приведение контуров к единой длине, сглаживание.
Перебор всех найденных контуров, поиск шаблона, максимально похожего на данный контур.
Слайд 10Дескриптор контура
Дескриптор – величина, характеризующая форму контура. При этом, близкие между
собой контуры должны иметь близкие дескрипторы.
АКФ инвариантно к переносу, вращению, масштабированию и выбору начальной точки. И кроме того,
АКФ является функцией одного контура
АКФ можно выбрать в качестве дескриптора, описывающего форму контура
АКФ инвариантно к переносу, вращению, масштабированию и выбору начальной точки. И кроме того,
АКФ является функцией одного контура
АКФ можно выбрать в качестве дескриптора, описывающего форму контура
Слайд 11Свертка АКФ
АКФ - вектор с k/2 значениями
Вейвлетная свертка позволит нам упорядочить
значения АКФ в масштабном порядке. Первым будет идти компонент, отвечающий наиболее крупномасштабным особенностям АКФ, а дальнейшие компоненты будут уточнять все более мелкие особенности АКФ
Слайд 12Особенности сравнения АКФ:
Сравнение АКФ, в общем случае, не избавляет нас от
необходимости вычисления ВКФ.
Иногда сравнения АКФ может быть достаточно для идентификации контуров.
Первый компонент свертки АКФ дает нам хороший дескриптор для упорядочивания базы шаблонов.
Иногда сравнения АКФ может быть достаточно для идентификации контуров.
Первый компонент свертки АКФ дает нам хороший дескриптор для упорядочивания базы шаблонов.
Свертка АКФ
Слайд 15Эквализация контуров
фиксируем длину ВК
для каждого исходного контура Г создаем вектор-контур N
длиной k
Слайд 16Эквализация контуров (2)
Если исходный контур больше необходимого, то перебираем все его
ЭВ, и считаем элементы N как сумму всех ЭВ, следующим образом:
Complex[] newPoint = new Сomplex[newCount];
for (int i = 0; i < Count; i++)
newPoint[i * newCount / Count] += this[i];
Complex[] newPoint = new Сomplex[newCount];
for (int i = 0; i < Count; i++)
newPoint[i * newCount / Count] += this[i];
Слайд 17Эквализация контуров (3)
исходный контур меньше k, то производим интерполяцию:
Complex[] newPoint =
new Complex[newCount];
for (int i = 0; i < newCount; i++)
{
double index = 1d * i * Count / newCount;
int j = (int)index;
double k = index - j;
newPoint[i] = this[j] * (1 - k) + this[j + 1] * k;
}
for (int i = 0; i < newCount; i++)
{
double index = 1d * i * Count / newCount;
int j = (int)index;
double k = index - j;
newPoint[i] = this[j] * (1 - k) + this[j + 1] * k;
}
Слайд 19Недостатки КА
описывает весь объект целиком, и не допускает никаких пересечений с
другими объектами или неполной видимости объекта
Слайд 20Заключение
Методы КА привлекательны своей простотой и быстродействием.
При наличии четко выраженного
объекта на контрастном фоне и отсутствии помех КА хорошо справляется с распознаванием.













![Эквализация контуров (3)исходный контур меньше k, то производим интерполяцию:Complex[] newPoint = new Complex[newCount];](/img/tmb/2/195224/a7d60ed042489ff739537d2811c3f94a-800x.jpg)








