ШКОЛЫ 120
ОВСЕПЯН ЮРИЙ
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комплeксные числа. Арифметические операции над ними (10 класс) презентация
Содержание
- 1. Комплeксные числа. Арифметические операции над ними (10 класс)
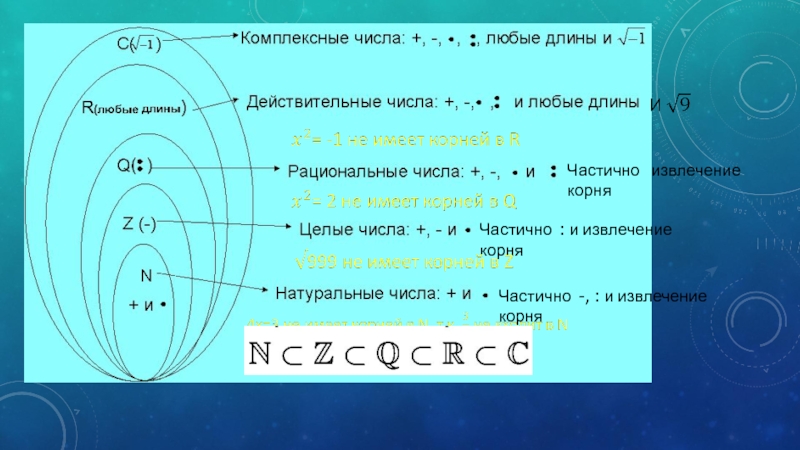
- 2. Частично -, : и извлечение
- 3.
- 4. УСЛОВИЯ, КОТОРЫМ ДОЛЖНЫ УДОВЛЕТВОРЯТЬ КОМПЛЕКСНЫЕ ЧИСЛА: С2)
- 5. УСЛОВИЯ, КОТОРЫМ ДОЛЖНЫ УДОВЛЕТВОРЯТЬ КОМПЛЕКСНЫЕ ЧИСЛА: С3-ОПЕРАЦИИ
- 6. Правила арифметических операций с
- 7. ОПРЕДЕЛЕНИЕ 1. КОМПЛЕКСНЫМ ЧИСЛОМ НАЗЫВАЮТ СУММУ ДЕЙСТВИТЕЛЬНОГО
- 8. ЕЩЕ СВОЙСТВА
Частично -, : и извлечение корня Частично : и извлечение корня Частично извлечение корня
Слайд 1КОМПЛEКСНЫЕ ЧИСЛА.
АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД НИМИ
ПРЕЗЕНТАЦИЮ ВЫПОЛНИЛ
УЧЕНИК 10А КЛАССА
МБОУ
Слайд 4УСЛОВИЯ, КОТОРЫМ ДОЛЖНЫ УДОВЛЕТВОРЯТЬ КОМПЛЕКСНЫЕ ЧИСЛА: С2) МНОЖЕСТВО КОМПЛЕКСНЫХ ЧИСЕЛ СОДЕРЖИТ ВСЕ
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА.
(ВОЗМОЖНОСТЬ УМНОЖАТЬ МНИМЫЕ ЕДИНИЦЫ
НА ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА)
Слайд 5УСЛОВИЯ, КОТОРЫМ ДОЛЖНЫ УДОВЛЕТВОРЯТЬ КОМПЛЕКСНЫЕ ЧИСЛА: С3-ОПЕРАЦИИ СЛОЖЕНИЯ, ВЫЧИТАНИЯ, УМНОЖЕНИЯ И ДЕЛЕНИЯ
КОМПЛЕКСНЫХ ЧИСЕЛ УДОВЛЕТВОРЯЮТ ОБЫЧНЫМ ЗАКОНАМ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ (СОЧЕТАТЕЛЬНОМУ, ПЕРЕМЕСТИТЕЛЬНОМУ, РАСПРЕДЕЛИТЕЛЬНОМУ).
Слайд 6
Правила арифметических операций
с чисто мнимыми числами:
ПУСТЬ ДАНО a+bi, где
a и b – любые действительные числа
Если а = 0, то а + bi = 0 + bi = bi — чисто мнимое число.
Если b = 0, a + bi = a + 0 = a — действительное число.
В остальных случаях суммы а + bi не являются ни действительными, ни чисто мнимыми числами, они являются новыми, более сложными, «составными» числами.
Если а = 0, то а + bi = 0 + bi = bi — чисто мнимое число.
Если b = 0, a + bi = a + 0 = a — действительное число.
В остальных случаях суммы а + bi не являются ни действительными, ни чисто мнимыми числами, они являются новыми, более сложными, «составными» числами.
Слайд 7ОПРЕДЕЛЕНИЕ 1. КОМПЛЕКСНЫМ ЧИСЛОМ НАЗЫВАЮТ СУММУ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА И ЧИСТО МНИМОГО
ЧИСЛА.
ОПРЕДЕЛЕНИЕ 2.
ДВА КОМПЛЕКСНЫХ ЧИСЛА НАЗЫВАЮТ РАВНЫМИ, ЕСЛИ РАВНЫ ИХ
ДЕЙСТВИТЕЛЬНЫЕ ЧАСТИ И РАВНЫ ИХ МНИМЫЕ ЧАСТИ:
а + bi = с + di <=> а = с, b = d.
