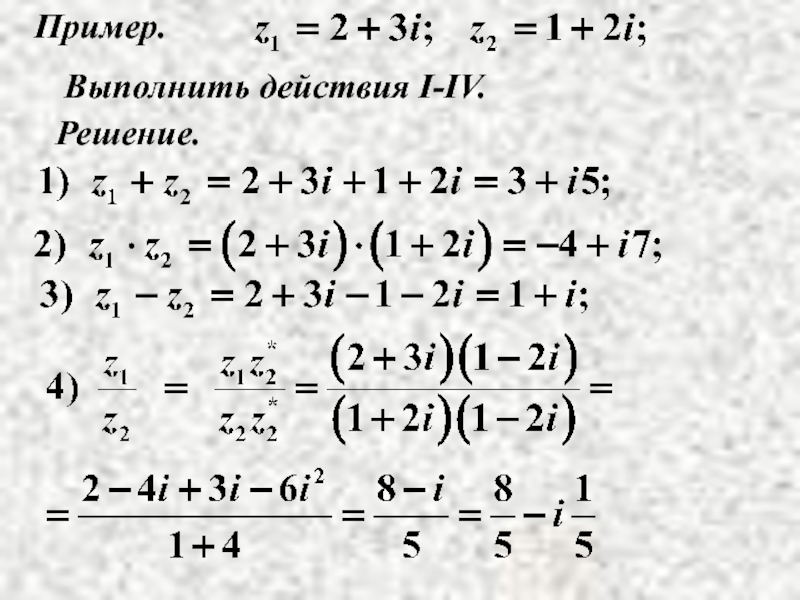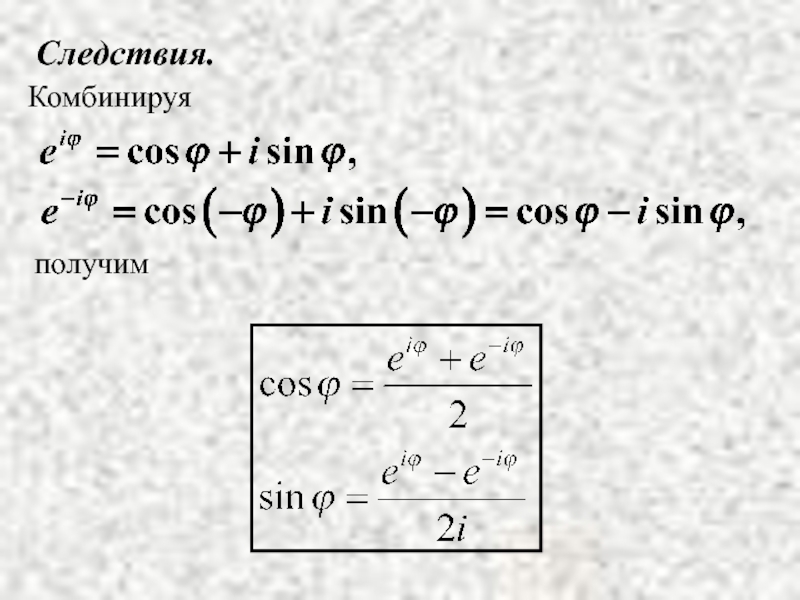- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комплексные числа презентация
Содержание
- 1. Комплексные числа
- 2. Лекция 3 2. Операции над комплексными числами. 1. Основные понятия. Комплексные числа
- 5. z=x+iy – это алгебраическая форма записи комплексного числа.
- 6. Операции над комплексными числами . I. Сложение. Рассмотрим комплексные числа в алгебраической форме: II. Умножение.
- 7. Вычислим
- 8. III. Вычитание (обратное сложению). IV. Деление (обратное умножению).
- 9. Чтобы выполнить деление, надо домножить числитель и знаменатель на число, сопряженное знаменателю:
- 10. В результате получим: Пользуясь алгебраической формой комплексного
- 11. Пример. Выполнить действия I-IV. Решение.
- 12. Изображение комплексных чисел на плоскости.
- 13. x y z = x+iy M(
- 14. Тригонометрическая и показательная формы записи комплексного числа.
- 15. Таким образом,
- 16. Обозначения. Формула Эйлера Запишем формулы Маклорена для функций
- 17. С учётом:
- 18. Из равенства правых частей следует: формула Эйлера.
- 19. Обозначения.
- 20. Следствия. получим
- 21. Пример. Записать это число в трёх формах, дать геометрическую интерпретацию. Решение.
- 22. Операции над комплексными числами в тригонометрической и показательной формах. Умножение: Рассмотрим
- 23. Деление:
- 24. Возведение в целую степень: Так как формула Муавра.
- 25. Здесь k может принимать все возможные целые
- 27. Замечание. Числа z0, z1,…, zn-1 имеют одинаковый
- 28. Пример. Обозначим Решение. Различных значений - четыре:
Лекция 3 2. Операции над комплексными числами. 1. Основные понятия. Комплексные числа
Слайд 6Операции над комплексными числами .
I. Сложение.
Рассмотрим комплексные числа в алгебраической форме:
II.
Умножение.
Слайд 9Чтобы выполнить деление, надо домножить числитель и знаменатель на число, сопряженное
знаменателю:
Слайд 10В результате получим:
Пользуясь алгебраической формой комплексного числа, можно производить операции сложения,
умножения и вычитания по обычным правилам для многочленов.
При делении комплексных чисел надо числитель и знаменатель домножить на сопряженное
знаменателю число.
Слайд 12Изображение комплексных чисел
на плоскости.
Плоскость, на которой изображаются комплексные числа
будем называть комплексной, ось абсцисс – действительной осью, ось ординат – мнимой осью.
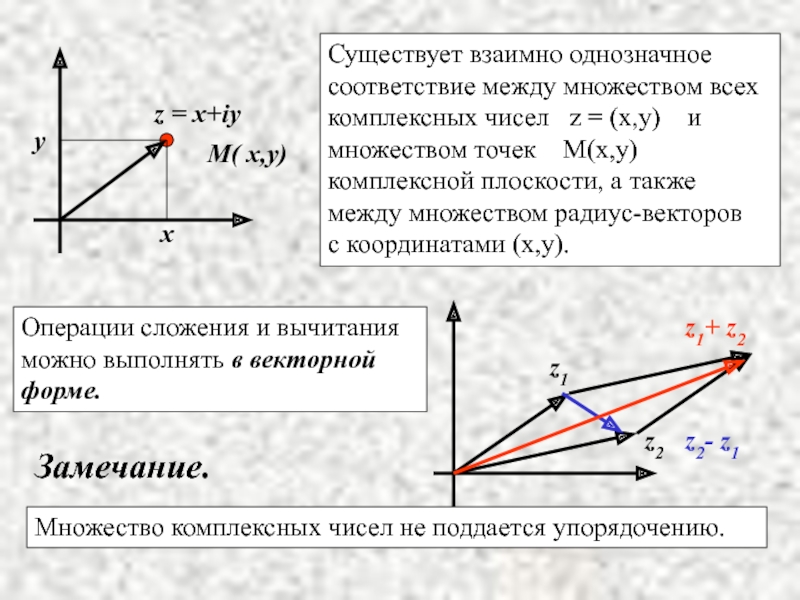
Слайд 13
x
y
z = x+iy
M( x,y)
Существует взаимно однозначное соответствие между множеством всех комплексных
чисел z = (x,y) и множеством точек M(x,y) комплексной плоскости, а также между множеством радиус-векторов с координатами (x,y).
Операции сложения и вычитания можно выполнять в векторной форме.
Замечание.
Множество комплексных чисел не поддается упорядочению.
Слайд 18Из равенства правых частей следует:
формула Эйлера.
По формуле Эйлера из (Т) следует
(П)
показательная
форма записи z .
Слайд 22Операции над комплексными числами
в тригонометрической и показательной
формах.
Умножение:
Рассмотрим
Слайд 25Здесь k может принимать все возможные целые значения, но различных (неодинаковых)
корней будет только n и они будут соответствовать числам k=0,1,2,3,…,(n-1):
Извлечение корня
(обратное возведению в степень):
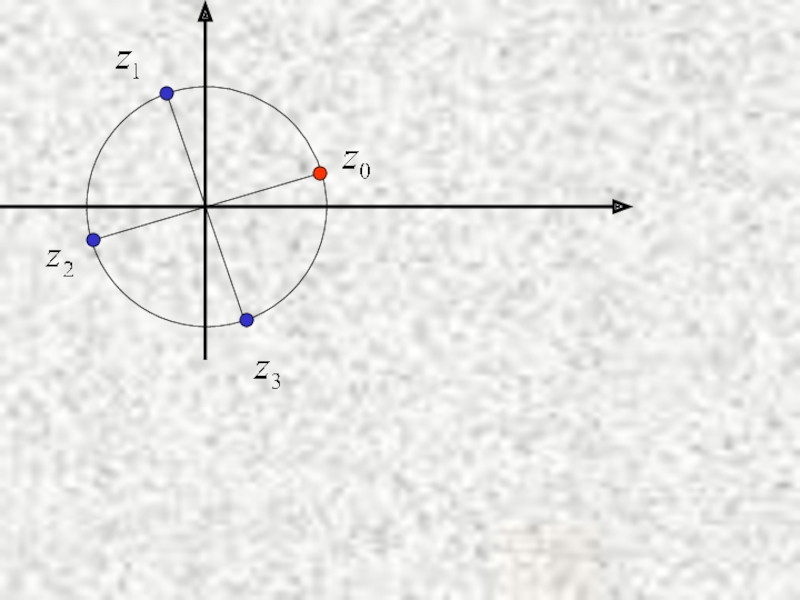
Слайд 27Замечание.
Числа z0, z1,…, zn-1 имеют одинаковый модуль
им соответствуют точки на
окружности радиуса
