- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пределы и непрерывность презентация
Содержание
- 1. Пределы и непрерывность
- 2. 6.1. ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ Если
- 3. Числа a1,a2…an называются членами последовательности, а
- 4. Изобразим члены последовательности (2) точками на
- 5. Последовательность {an} называется ограниченной сверху
- 6. Последовательность {an} называется ограниченной, если она ограничена сверху и снизу:
- 7. Последовательность (1) ограничена снизу, но не
- 8. Число А называется пределом числовой
- 9. Последовательность, имеющая предел, называется сходящейся. В
- 10. ПРИМЕР. Дана последовательность Показать, что предел этой последовательности равен 1. 3
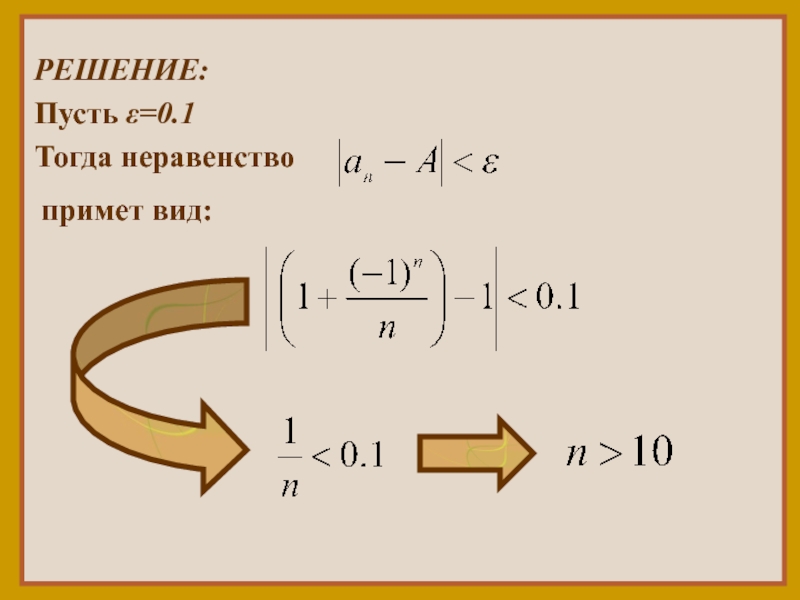
- 11. РЕШЕНИЕ: Пусть ε=0.1 Тогда неравенство примет вид:
- 12. Если ε=0.01, то неравенство выполняется при
- 13. Рассмотрим геометрический смысл предела числовой последовательности.
- 14. Неравенство
- 15. Т.е. число А есть предел числовой
Слайд 2
6.1. ПРЕДЕЛ ЧИСЛОВОЙ
ПОСЛЕДОВАТЕЛЬНОСТИ
Если каждому натуральному числу n по
некоторому закону
определенное число an , то говорят, что
задана числовая последовательность
Слайд 3
Числа a1,a2…an называются членами последовательности, а число an называется общим членом
Например:
1
2
Слайд 4
Изобразим члены последовательности (2) точками на числовой оси.
Можно заметить, что члены
Слайд 5
Последовательность {an} называется
ограниченной сверху (снизу), если существует
такое число М
последовательности удовлетворяет
неравенству:
Слайд 7
Последовательность (1) ограничена снизу, но не сверху.
Последовательность (2) ограничена, т.к. все
Если выполняется условие
то последовательность называется возрастающей.
Если выполняется условие
то последовательность называется убывающей.
Последовательность (1) возрастающая.
Последовательность (2) убывающая.
Слайд 8
Число А называется пределом числовой
последовательности {an}, если для любого,
сколь угодно
номер N, что при всех n>N, выполняется
неравенство:
Слайд 9
Последовательность, имеющая предел, называется сходящейся.
В противном случае последовательность расходящаяся.
Смысл определения предела
последовательности:
Для достаточно больших номеров n члены
последовательности очень мало отличаются от
числа А (меньше, чем на число , ε , каким бы
малым оно не было).
Слайд 12
Если ε=0.01, то неравенство выполняется при
Для любого ε >0, неравенство
Т.е. для любого ε >0 существует номер
Что для всех n>N, выполняется неравенство:
Слайд 13
Рассмотрим геометрический смысл предела числовой последовательности. Для этого изобразим члены последовательности
Слайд 14
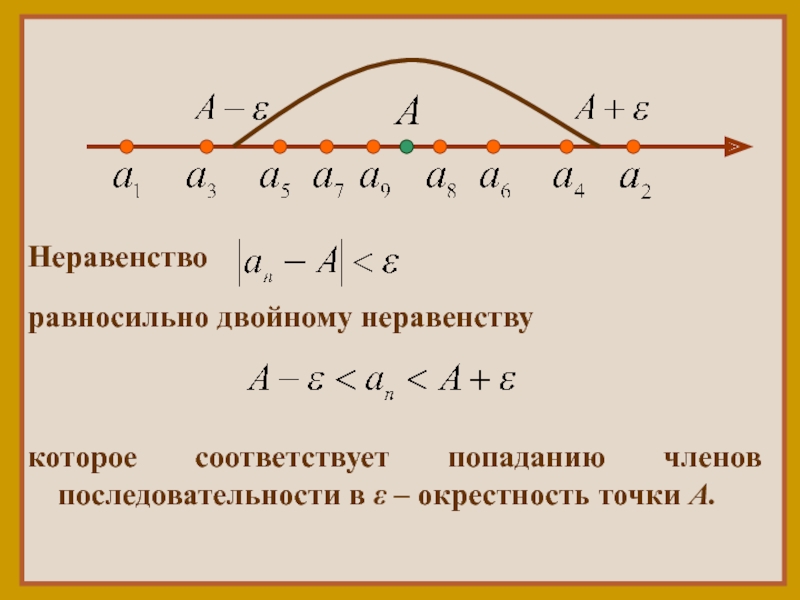
Неравенство
равносильно двойному неравенству
которое соответствует попаданию членов последовательности в ε
Слайд 15
Т.е. число А есть предел числовой последовательности {an}, если для любого,
Вне этой окрестности может быть только конечное число членов последовательности.