- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Компланарные векторы. (10 класс) презентация
Содержание
- 1. Компланарные векторы. (10 класс)
- 2. Векторы называются компланарными, если
- 4. Три произвольных
- 5. Три произвольных
- 6. B C A1
- 7. A B
- 8. №355 Дан параллелепипед
- 9. №355 Дан параллелепипед
- 10. №355 Дан параллелепипед
- 11. №355 Дан параллелепипед
- 12. Любые два вектора компланарны. Три вектора, среди которых имеются два коллинеарных, также компланарны. Признак компланарности
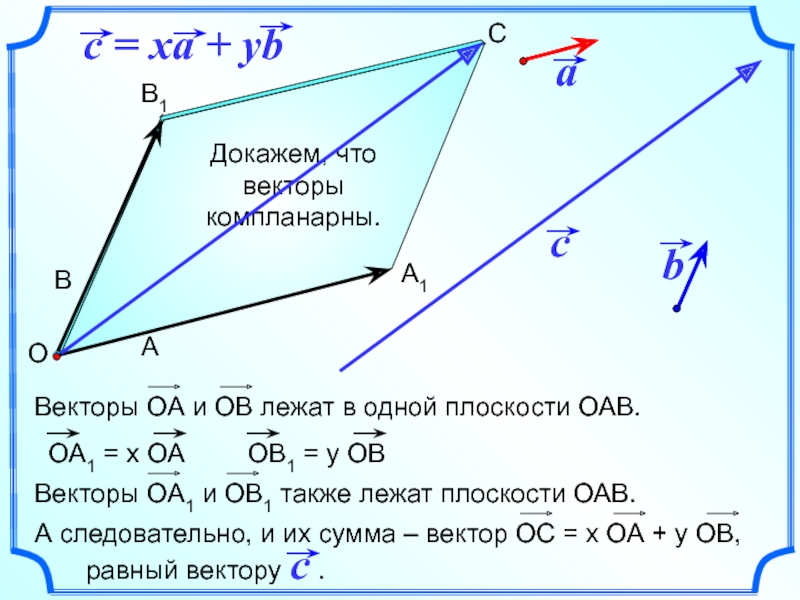
- 13. Докажем, что векторы компланарны. В1
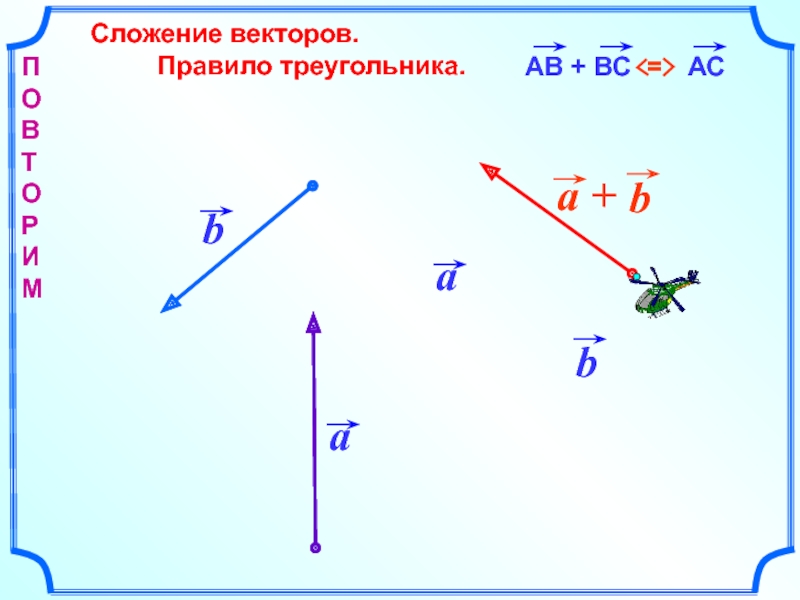
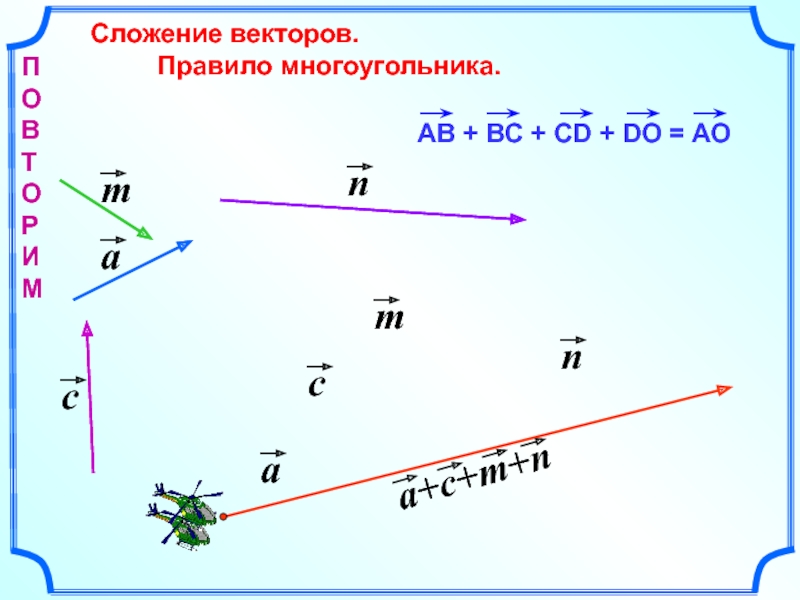
- 15. Сложение векторов.
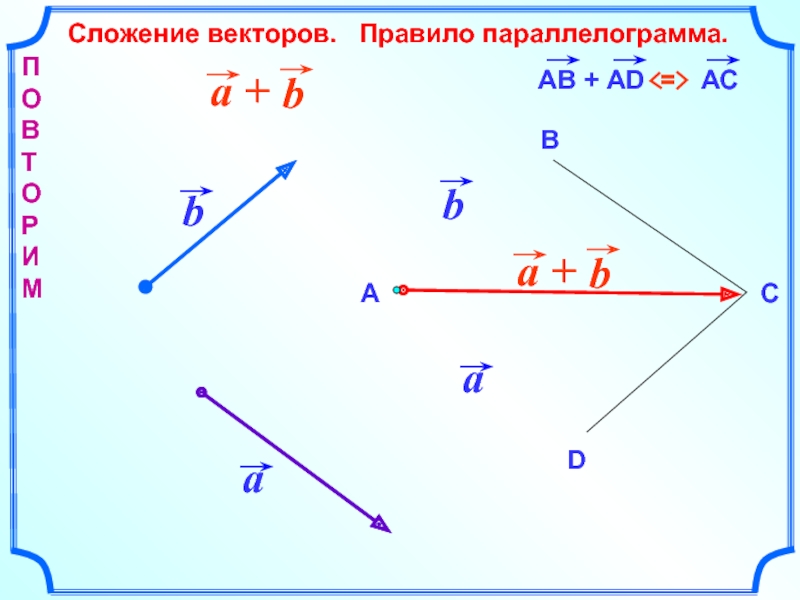
- 16. Сложение векторов. Правило параллелограмма.
- 17. Сложение векторов.
- 19. В A С
- 20. В A С C1
- 21. В A С
- 22. В A С
- 23. В A С
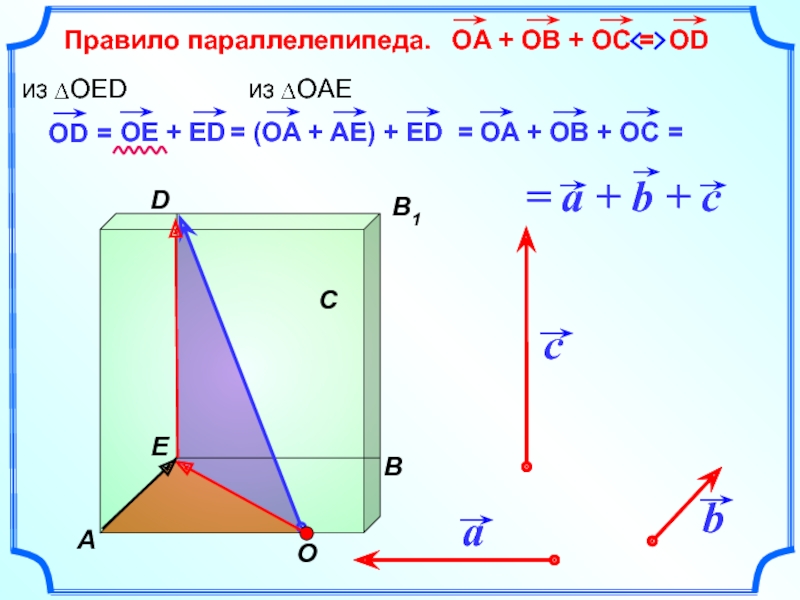
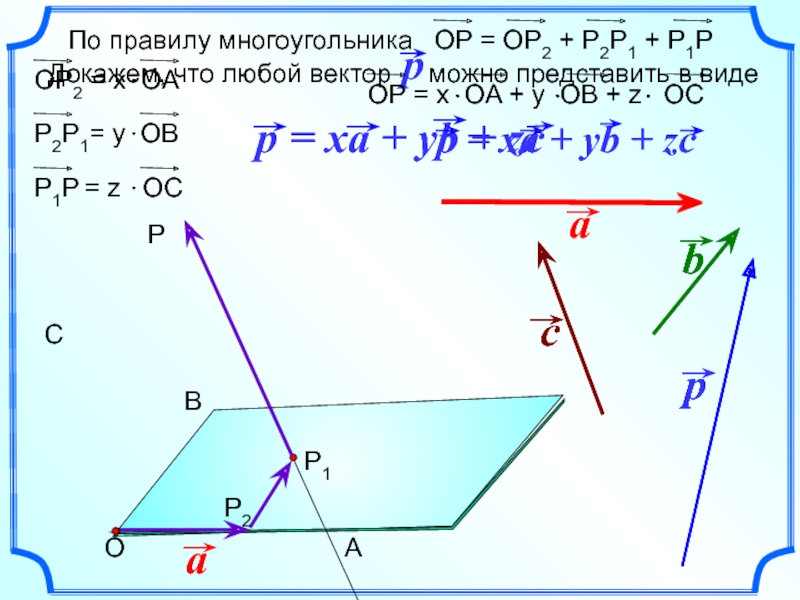
- 24. Теорема о разложении вектора по трем некомпланарным
- 25. C B P1 A P P2
- 26. Докажем теперь, что коэффициенты разложения
- 27. В A С
- 28. В A С
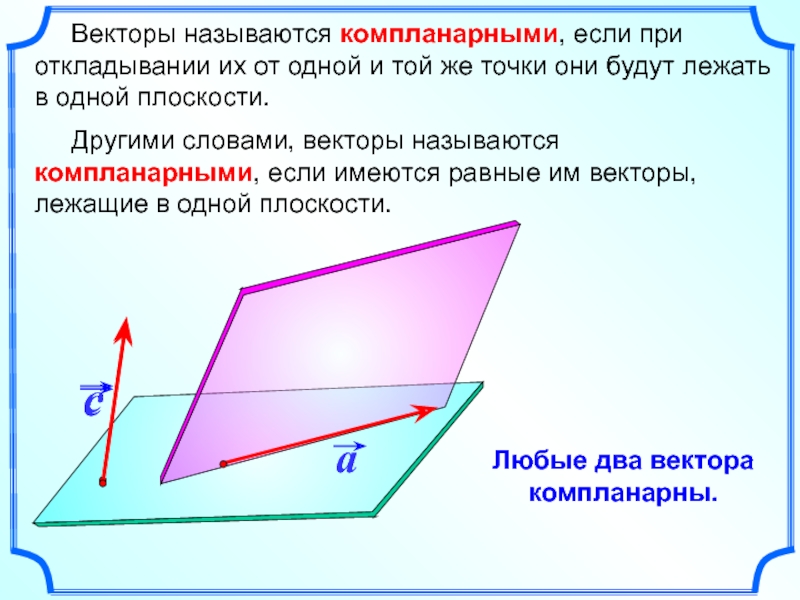
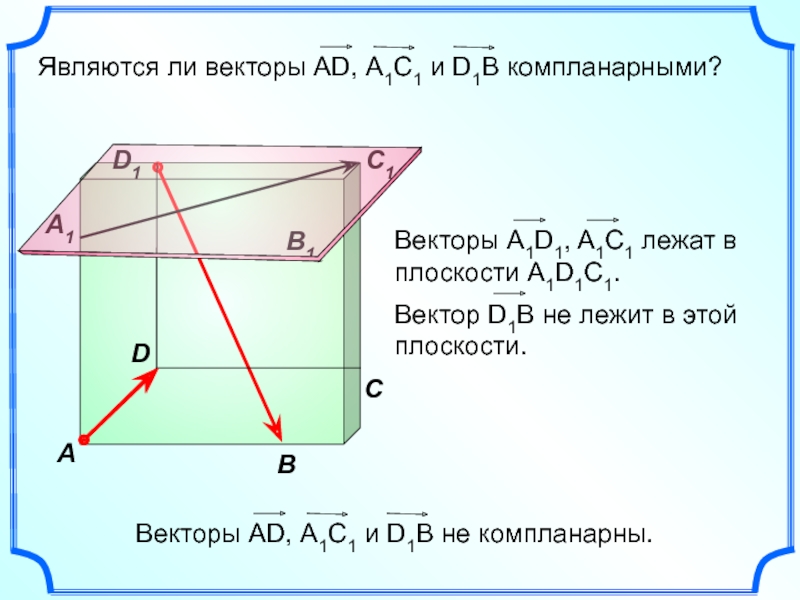
Слайд 2 Векторы называются компланарными, если при откладывании их от
Другими словами, векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
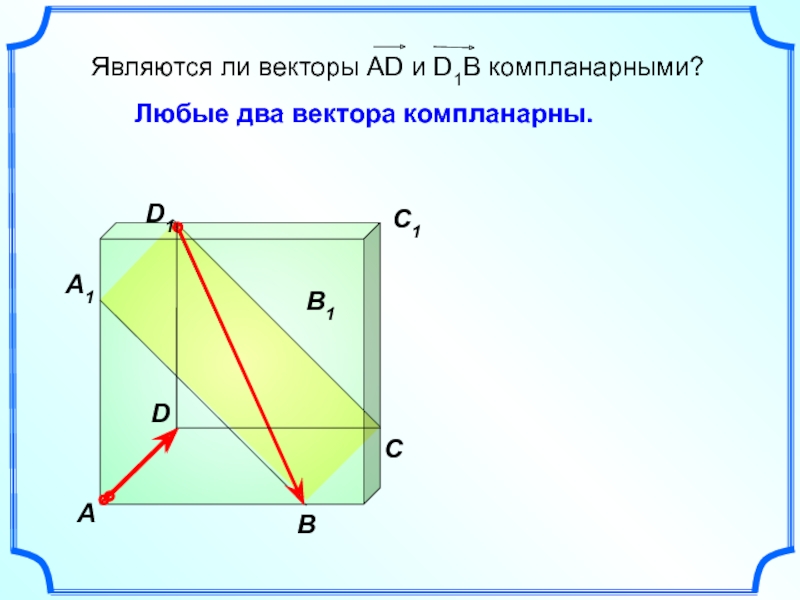
Любые два вектора компланарны.
Слайд 4
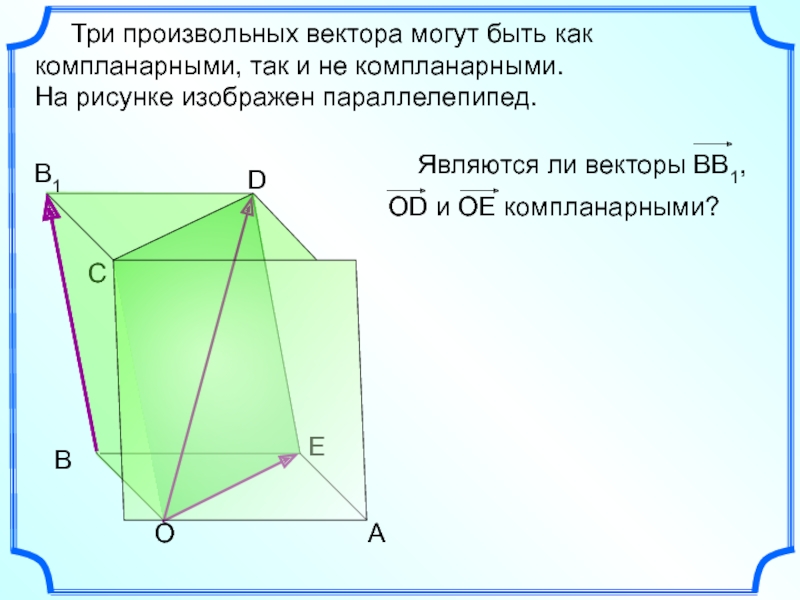
Три произвольных вектора могут быть как компланарными, так
На рисунке изображен параллелепипед.
А
О
Е
D
C
В
B1
Слайд 5
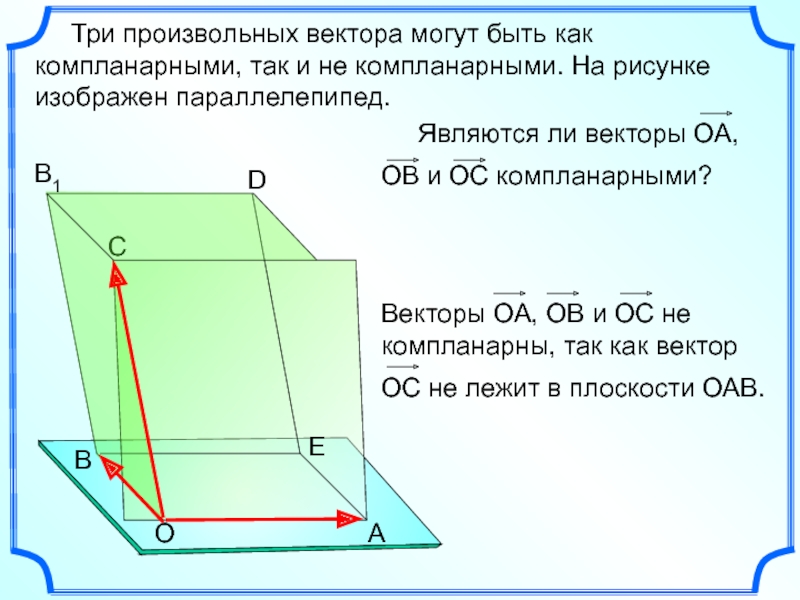
Три произвольных вектора могут быть как компланарными, так
А
О
Е
D
C
В
B1
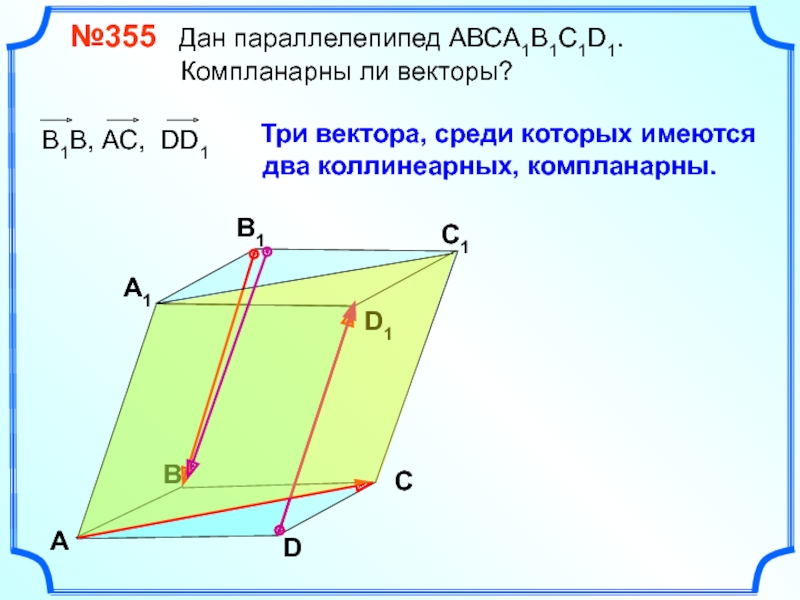
Слайд 8
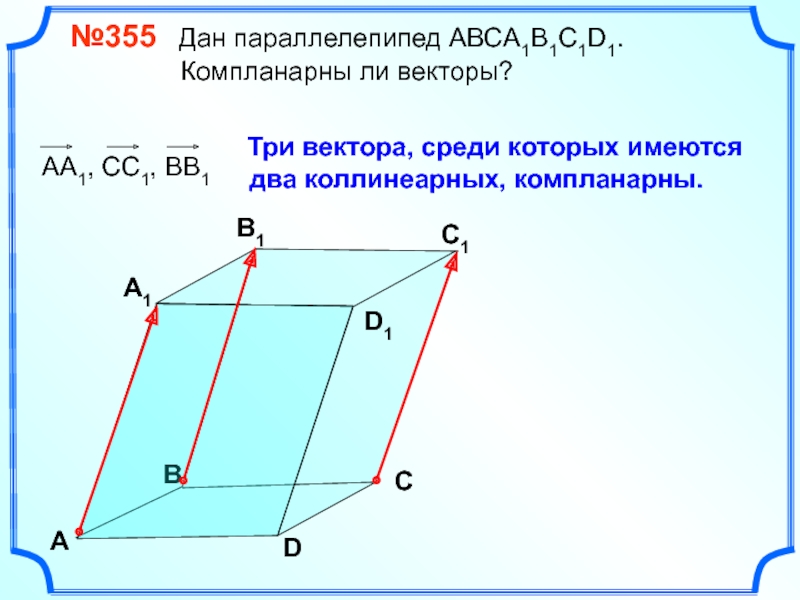
№355 Дан параллелепипед АВСA1B1C1D1.
В
А
В1
С1
D1
D
С
А1
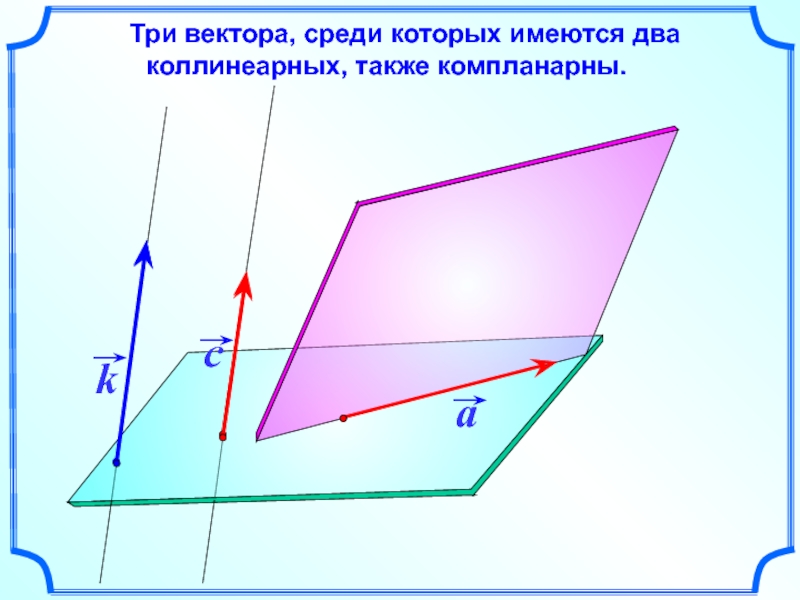
Три вектора, среди которых имеются
два коллинеарных, компланарны.
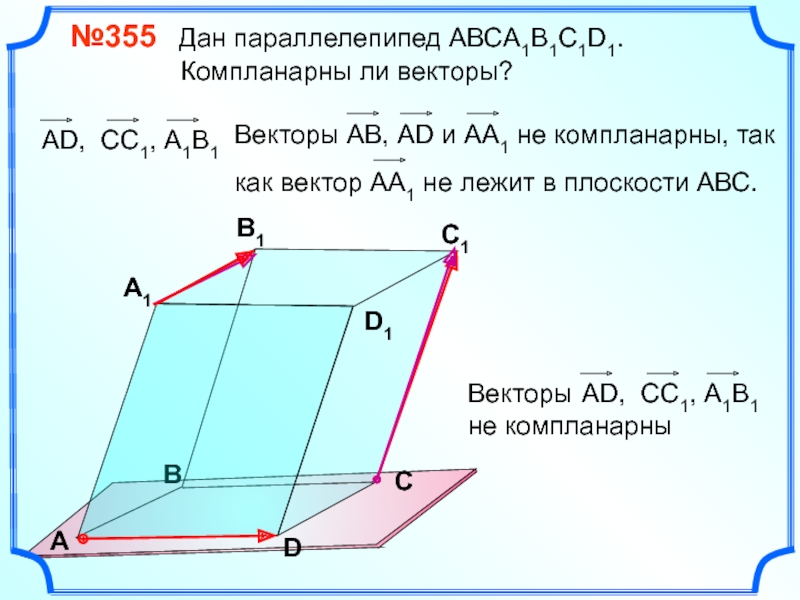
Слайд 10
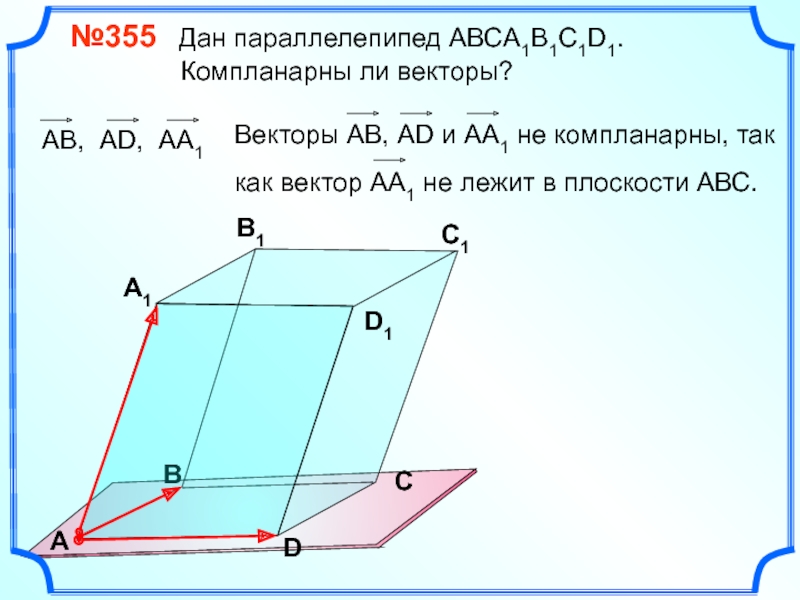
№355 Дан параллелепипед АВСA1B1C1D1.
В
А
В1
С1
D1
D
С
А1
Три вектора, среди которых имеются
два коллинеарных, компланарны.
Слайд 12Любые два вектора компланарны.
Три вектора, среди которых имеются два коллинеарных, также
Признак компланарности
Слайд 19
В
A
С
B1
C1
D1
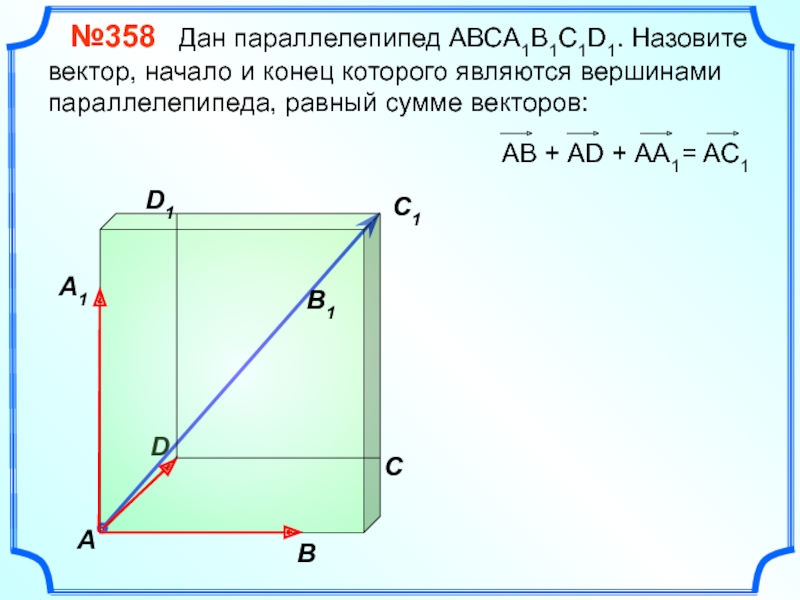
№358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало
АВ + АD + АА1
A1
Слайд 20В
A
С
C1
D1
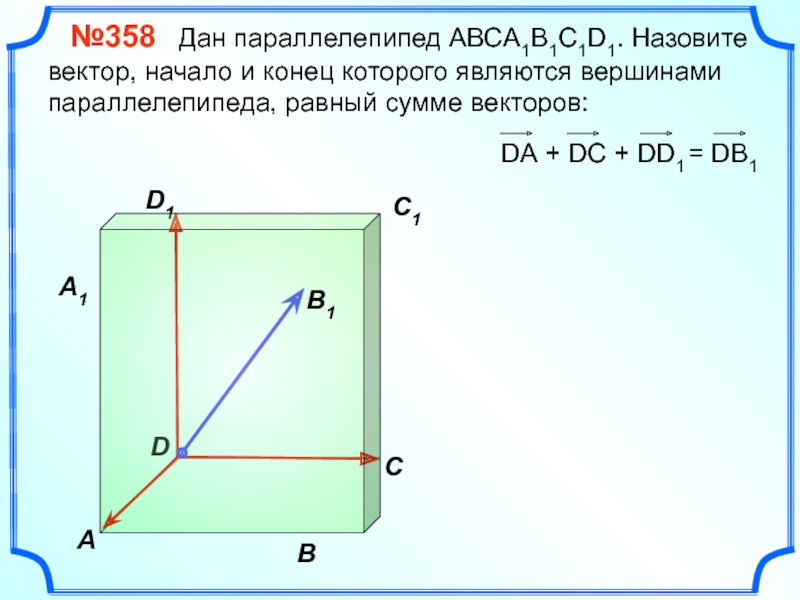
№358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и
DА + DC + DD1
A1
B1
Слайд 21
В
A
С
C1
D1
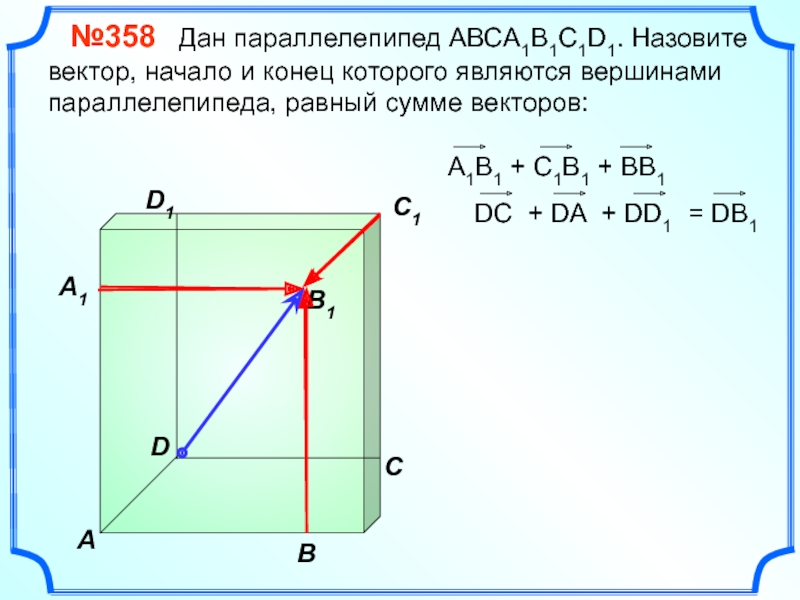
№358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и
A1
B1
A1B1 + C1B1 + BB1
Слайд 22
В
A
С
C1
D1
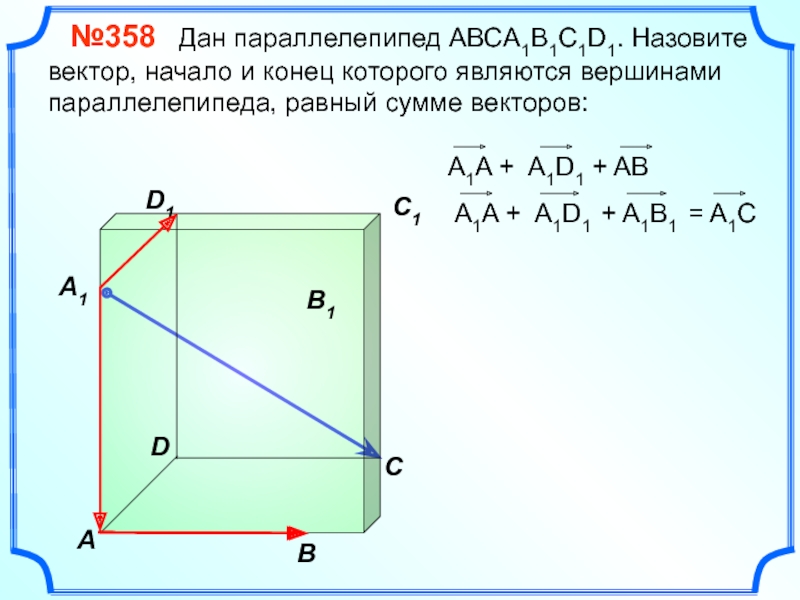
№358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и
A1
B1
Слайд 23
В
A
С
C1
D1
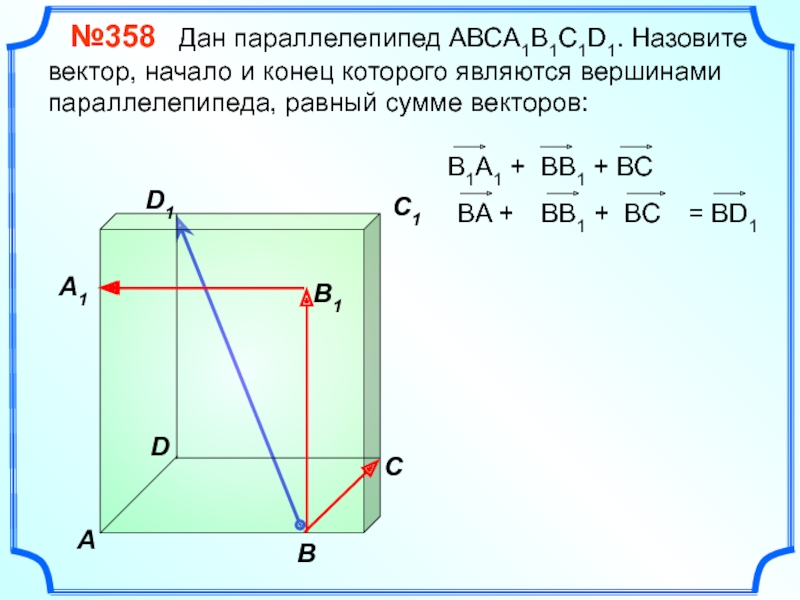
№358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и
A1
B1
Слайд 24Теорема о разложении вектора по трем некомпланарным векорам.
Слайд 26 Докажем теперь, что коэффициенты разложения определяются единственным образом. Допустим,
–
Это равенство выполняется только тогда,
когда
o
o
o
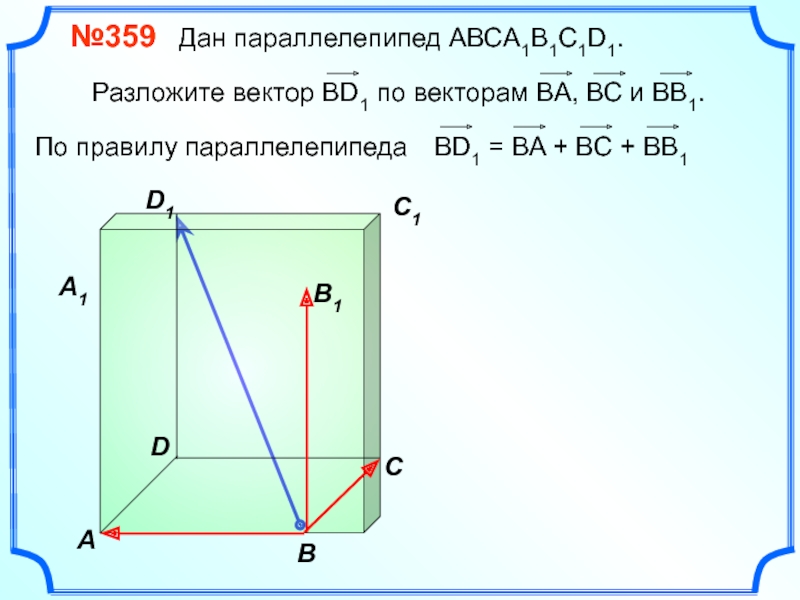
Слайд 27
В
A
С
C1
D1
№359 Дан параллелепипед АВСA1B1C1D1.
A1
B1
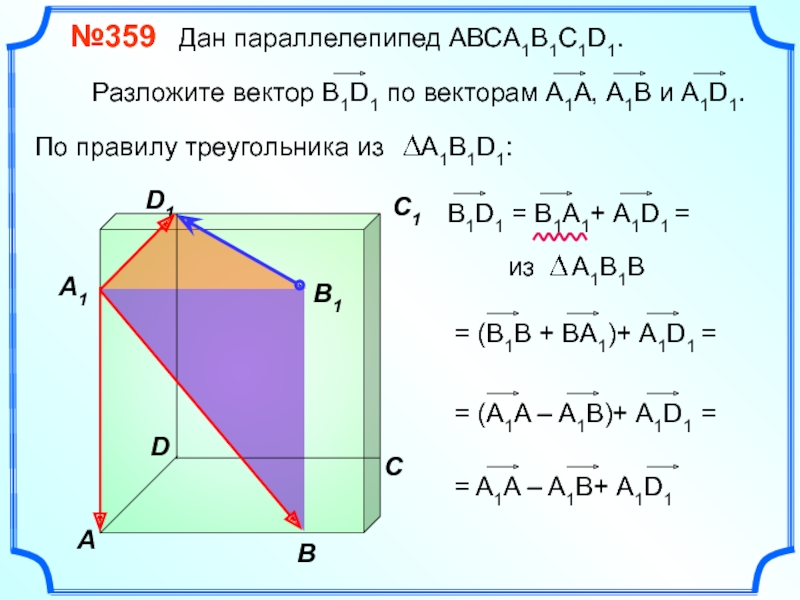
Слайд 28
В
A
С
C1
D1
№359 Дан параллелепипед АВСA1B1C1D1.
A1
B1
=
=
=