- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комбинаторика. Правило суммы. Правило произведения презентация
Содержание
- 1. Комбинаторика. Правило суммы. Правило произведения
- 2. Оглавление Что такое комбинаторика? Факториал Перестановки. Размещения.
- 3. Термин «комбинаторика» происходит от латинского слова «combina»,
- 4. Произведение всех последовательных натуральных чисел от 1
- 5. Перестановки. Размещения. Комбинации
- 6. Правило суммы. Правило произведения
- 7. Задача 1 На завтрак Вова может
- 8. Ответ:15. Переберем все возможные варианты
- 9. Задача 2 Несколько стран в
- 10. Ответ:6.
- 11. На соревнование по легкой атлетике приехала команда
- 12. Поскольку тренеру важно, в каком порядке будут
- 13. Задача 4 Сколько четных двузначных чисел можно составить из цифр 0,1,2,4,5,9?
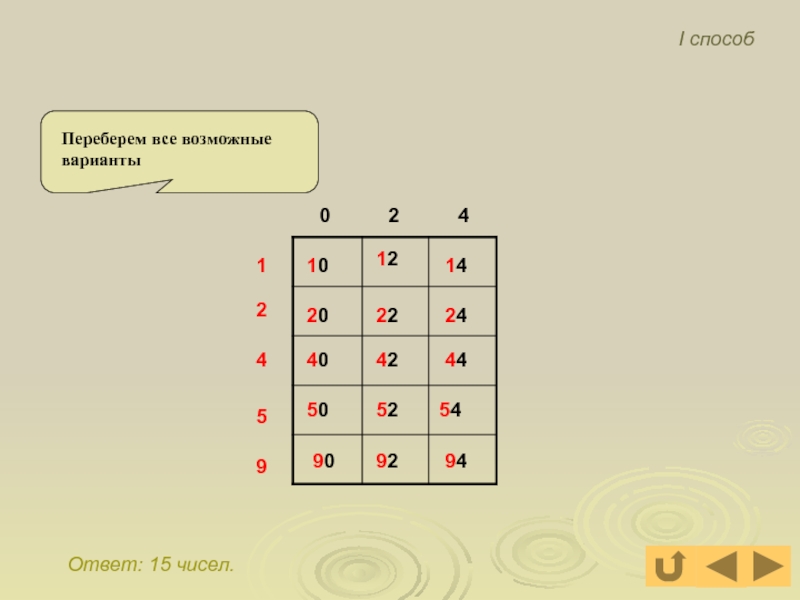
- 14. Ответ: 15 чисел. 1 2 4
- 15. Воспользуемся формулой комбинаций без
- 16. В коридоре висят три лампочки. Сколько имеется
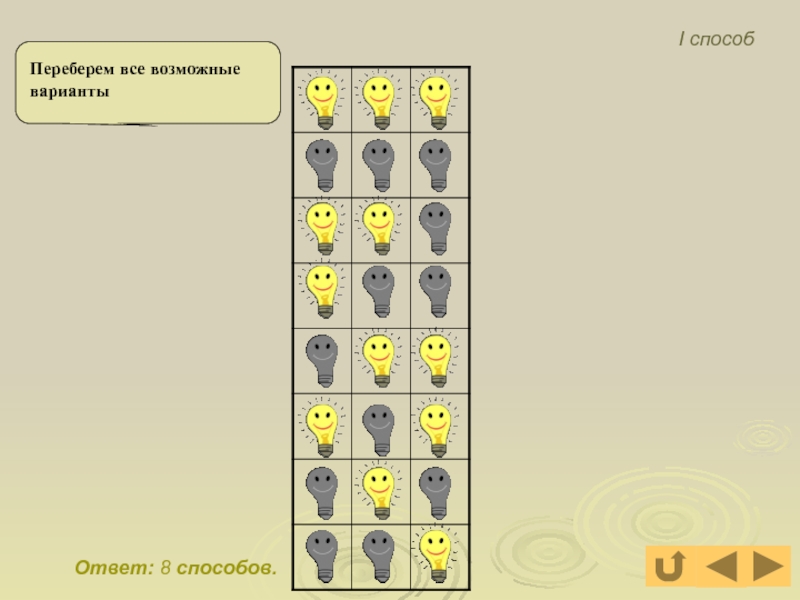
- 17. Ответ: 8 способов. Переберем все возможные варианты І способ
- 18. Воспользуемся правилом умножения Для каждой лампочки
- 19. Выберите правило №1. Из города А
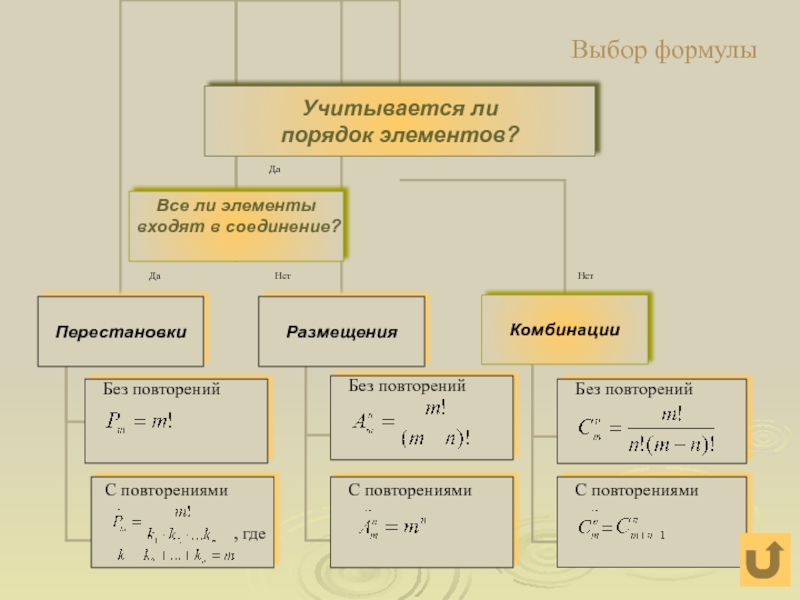
- 20. Да Нет Нет Выбор формулы
Слайд 2Оглавление
Что такое комбинаторика?
Факториал
Перестановки. Размещения. Комбинации
Правила суммы, произведения
Примеры решения задач
Выбор формулы
Слайд 3 Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на
Комбинаторика - раздел математики, посвящённый решению задач выбора и расположения элементов в соответствии с данными условиями.
Знание комбинаторики необходимо представителям самых разных специальностей. С комбинаторными задачами приходится иметь дело физикам, химикам, биологам, лингвистам, криптографам и другим специалистам.
Слайд 4Произведение всех последовательных натуральных чисел от 1 до n обозначается n!
Читаем:
n!
n (эн) - факториал
n! = 1 · 2 · 3 · ... · n
Слайд 7
Задача 1
На завтрак Вова может выбрать: плюшку, бутерброд,
пряник, или кекс,
кефиром. Сколько возможных вариантов завтрака?
Слайд 9
Задача 2
Несколько стран в качестве символа своего государства решили использовать флаг
Слайд 11 На соревнование по легкой атлетике приехала команда из 12-ти спортсменок. Сколькими
Задача 3
Слайд 12Поскольку тренеру важно, в каком порядке будут бежать спортсменки, то порядок
Ответ: 11 880.
Слайд 14Ответ: 15 чисел.
1
2
4
5
9
0
2
4
10
14
12
20
22
24
40
42
44
50
52
54
90
92
94
Переберем все возможные варианты
І способ
Слайд 15
Воспользуемся формулой комбинаций без повторений
Поскольку нам необходимо составить двузначные числа, то
Чтобы число было четным, оно должно заканчиваться на 0, 2 или 4, т.е. четное число можно выбрать способами .
Тогда по правилу произведения четные двузначные числа можно составить .
Получаем
ІI способ
Ответ:15 чисел.
Слайд 16В коридоре висят три лампочки. Сколько имеется различных способов освещения коридора?
Задача
Слайд 18
Воспользуемся правилом умножения
Для каждой лампочки возможны два исхода, а лампочек три,
Ответ:8.
Нам необходимо разместить 2 предмета по трем ячейкам, причем они могут повторяться. Имеем:
Воспользуемся формулой размещений с повторениями
ІІ способ
ІІІ способ
Слайд 19Выберите правило
№1. Из города А а город В ведут 5 дорог,
5*3=15
№2. На книжной полке стоят 3 книги по алгебре, 4 по геометрии и 5 по литературе. Сколькими способами можно взять с полки одну книгу по математике?
4+3=7
№3. В меню имеется 4 первых блюда, 3 – вторых, 2 – десерта. Сколько различных обедов можно из них составить?
4*3*2=24