- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Командное задание. Численное интегрирование презентация
Содержание
- 1. Командное задание. Численное интегрирование
- 2. Метод Симпсона (парабол) Задача нахождения
- 3. Метод парабол (Симпсона) - суть метода, формула, оценка погрешности, иллюстрация.
- 4. Метод парабол (Симпсона) - суть метода, формула,
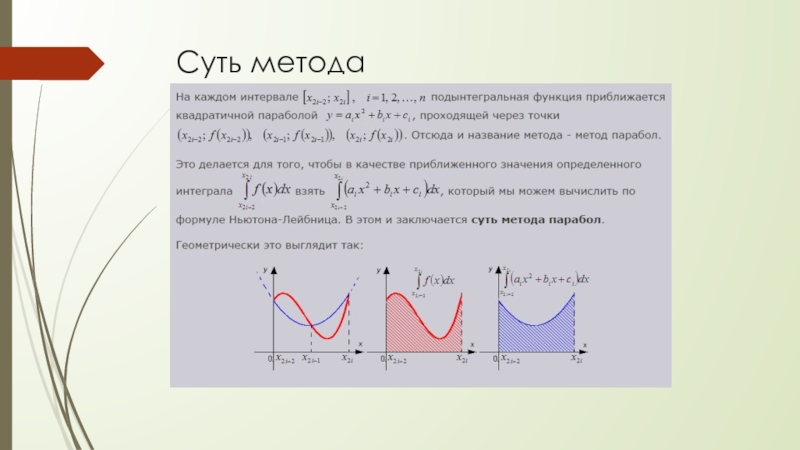
- 5. Суть метода
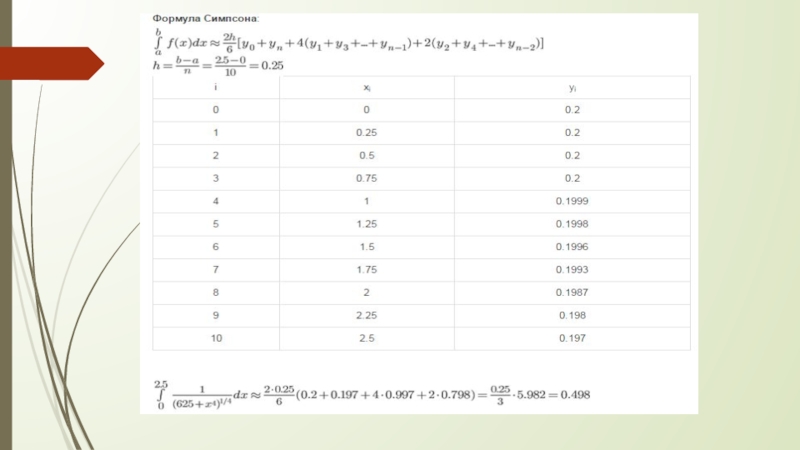
- 6. Задание Интеграл Решить его методом Симпсона с приближенным к 0.001 значению
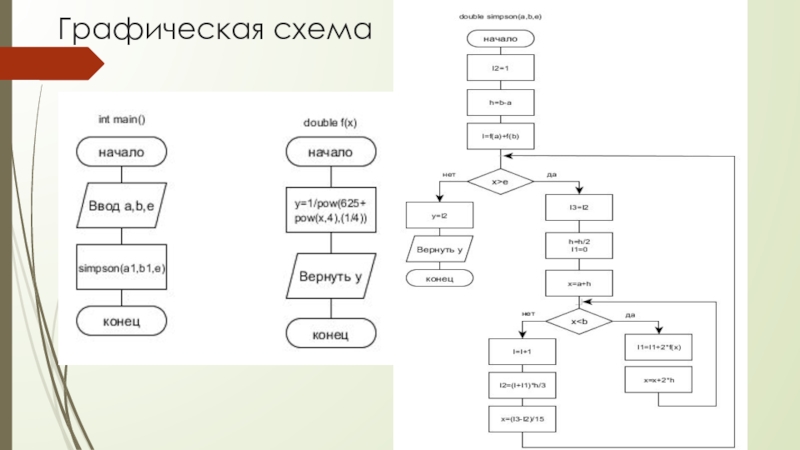
- 8. Графическая схема
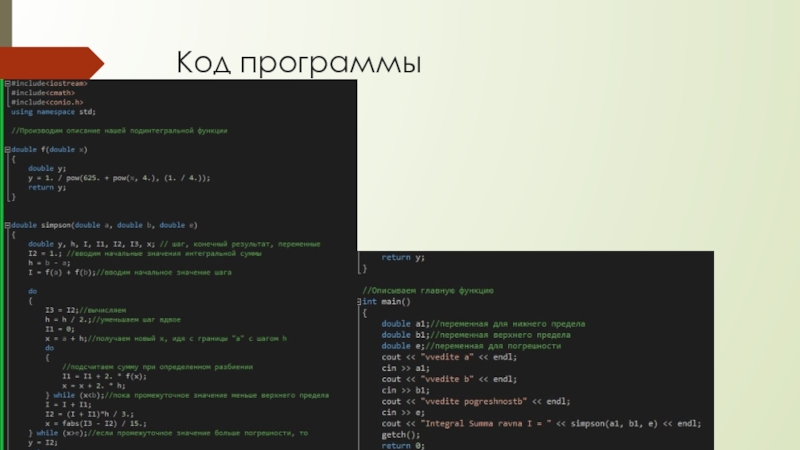
- 9. Код программы
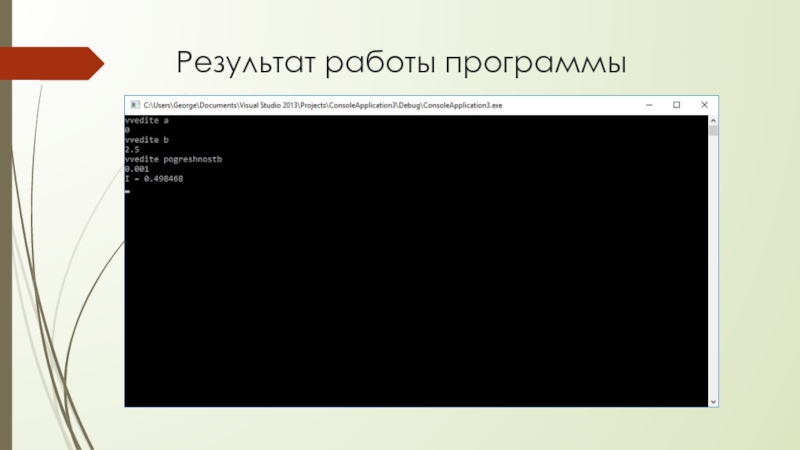
- 10. Результат работы программы
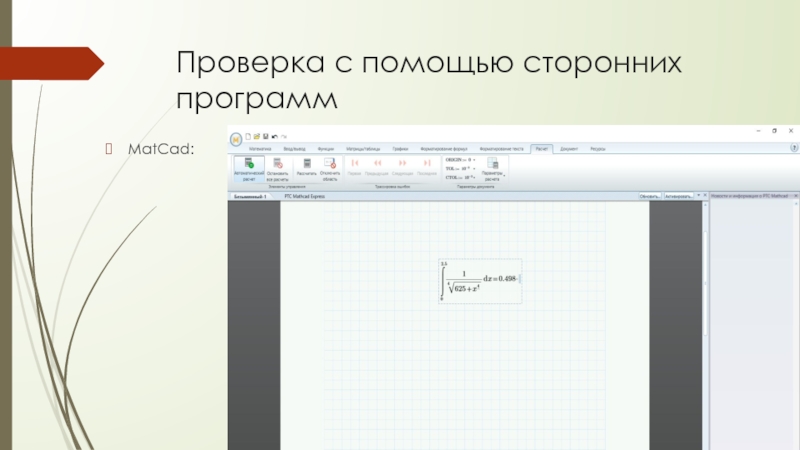
- 11. Проверка с помощью сторонних программ MatCad:
- 12. Источники Википедия MathProfi.ru
- 13. Спасибо за внимание
Слайд 1Командное задание «численное интегрирование» метод Симпсона
Студенты : Грачев Владимир
Быков Георгий
Зубаиров Тимур
Слайд 2
Метод Симпсона (парабол)
Задача нахождения точного значения определенного интеграла не всегда имеет
решение. Действительно, первообразную подынтегральной функции во многих случаях не удается представить в виде элементарной функции. В этом случае мы не можем точно вычислить определенный интеграл по формуле Ньютона-Лейбница. Однако есть методы численного интегрирования, позволяющие получить значение определенного интеграла с требуемой степенью точности. Одним из таких методов является метод Симпсона (его еще называют методом парабол). Сначала выясним смысл метода парабол, дадим графическую иллюстрацию и выведем формулу для вычисления приближенного значения интеграла. Далее запишем неравенство для оценки абсолютной погрешности метода Симпсона (парабол).
Слайд 4Метод парабол (Симпсона) - суть метода, формула,
оценка погрешности, иллюстрация.
– сумма первого и последнего значения подынтегральной функции;
– сумма членов с чётными индексами умножается на 2;
– сумма членов с нечётными индексами умножается на 4.
Метод Симпсона (метод парабол)Способ при котором – график подынтегральной функции приближается не ломаной линией, а маленькими параболами. Сколько промежуточных отрезков – столько и маленьких парабол. Если взять те же три отрезка, то метод Симпсона даст ещё более точное приближение, чем метод прямоугольников или метод трапеций.
– сумма членов с чётными индексами умножается на 2;
– сумма членов с нечётными индексами умножается на 4.
Метод Симпсона (метод парабол)Способ при котором – график подынтегральной функции приближается не ломаной линией, а маленькими параболами. Сколько промежуточных отрезков – столько и маленьких парабол. Если взять те же три отрезка, то метод Симпсона даст ещё более точное приближение, чем метод прямоугольников или метод трапеций.