к окружности
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Касательная к окружности презентация
Содержание
- 1. Касательная к окружности
- 2. Взаимное расположение прямой и окружности r
- 3. Взаимное расположение прямой и окружности
- 4. Взаимное расположение прямой и окружности r
- 5. Свойство касательной. Касательная к окружности перпендикулярна
- 7. Даны прямоугольник
- 9. 600
- 10. 600
- 11. 300
- 12. Отрезки касательных к окружности,
- 13. Признак касательной. О r
- 14. Прямая АВ касается окружности с центром
- 15. Прямая АВ касается окружности с центром
- 16. А В
- 17. В О
- 18. В О
- 19. 4 В О
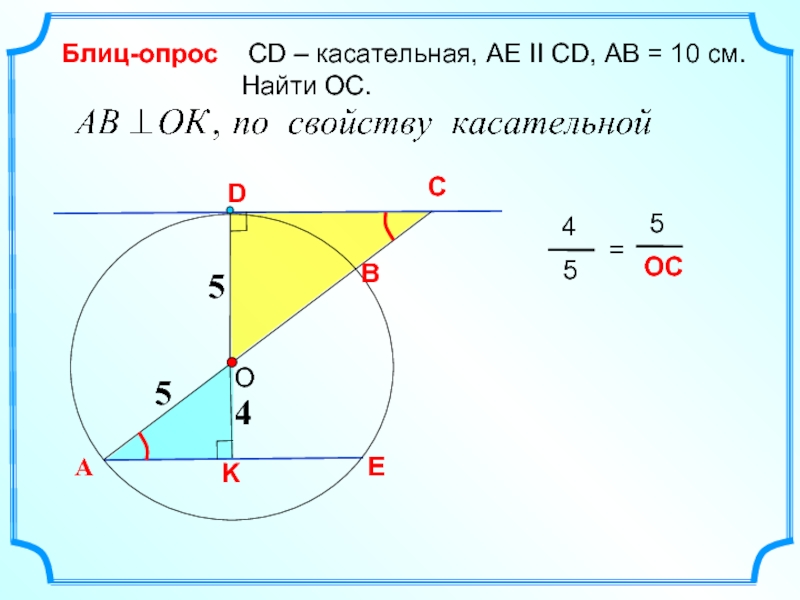
- 20. C СD – касательная,
Взаимное расположение прямой и окружности r d > r Окружность и прямая не имеют общих точек
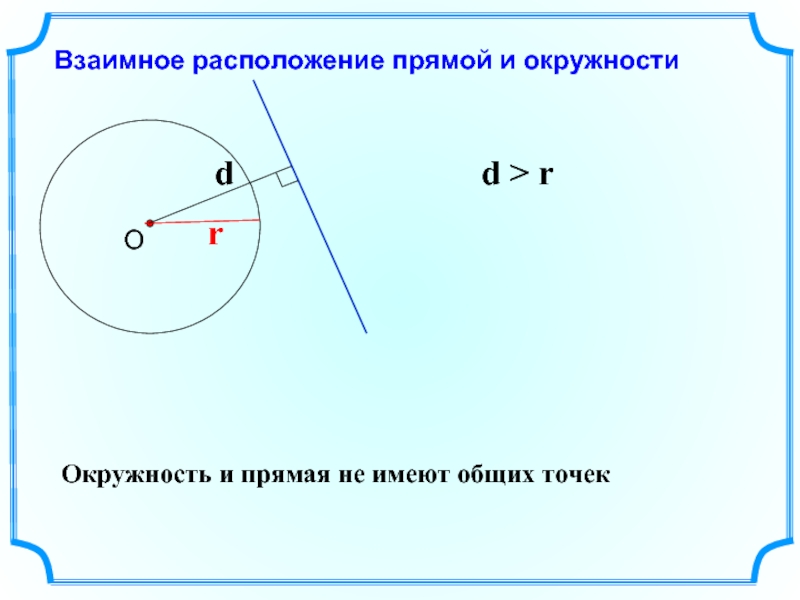
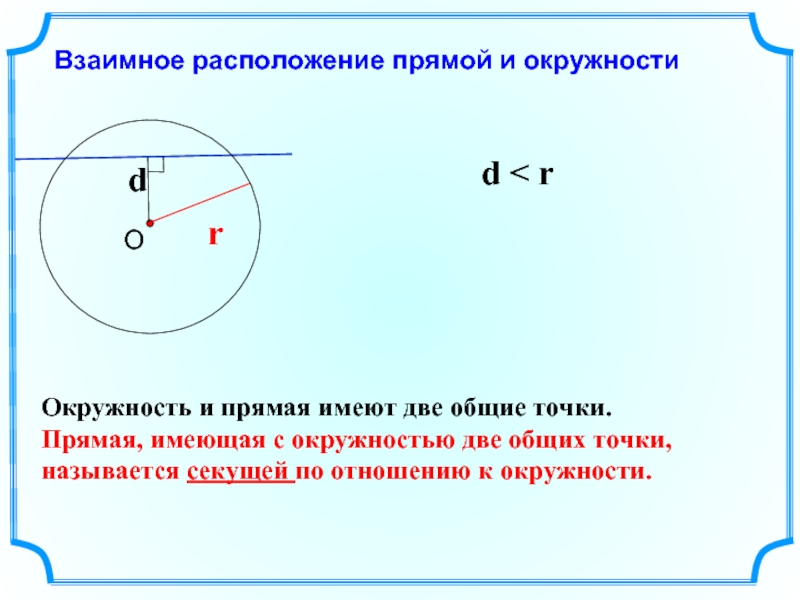
Слайд 3Взаимное расположение прямой и окружности
d
r
d < r
Окружность и прямая имеют две
общие точки.
Прямая, имеющая с окружностью две общих точки, называется секущей по отношению к окружности.
Прямая, имеющая с окружностью две общих точки, называется секущей по отношению к окружности.
Слайд 4
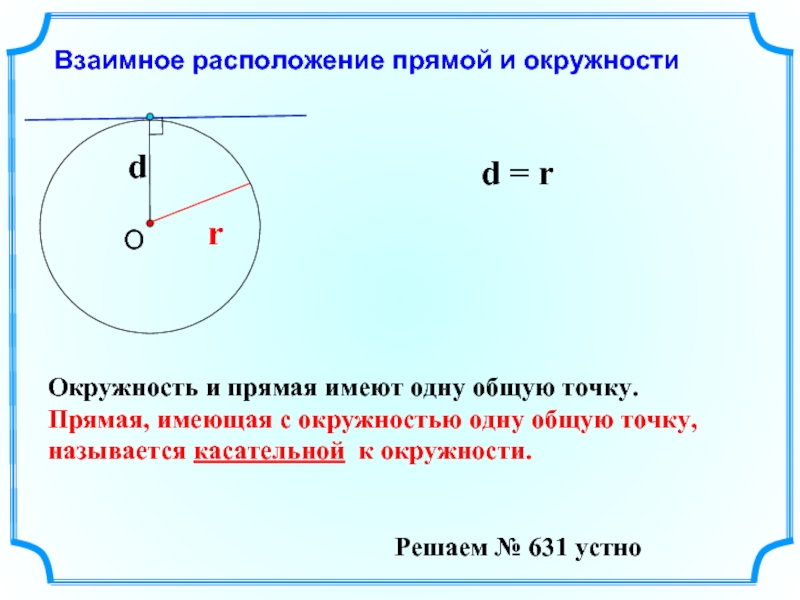
Взаимное расположение прямой и окружности
r
d = r
Окружность и прямая имеют одну
общую точку.
Прямая, имеющая с окружностью одну общую точку, называется касательной к окружности.
Прямая, имеющая с окружностью одну общую точку, называется касательной к окружности.
Решаем № 631 устно
Слайд 5
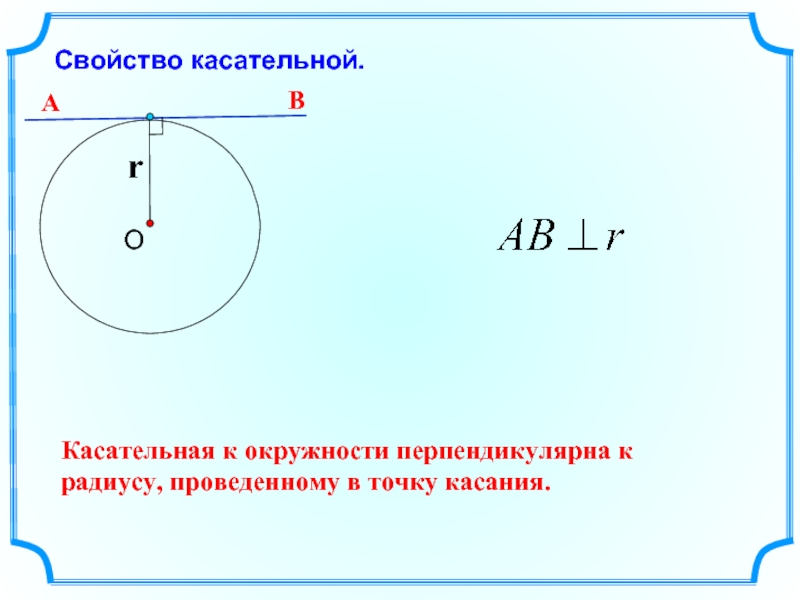
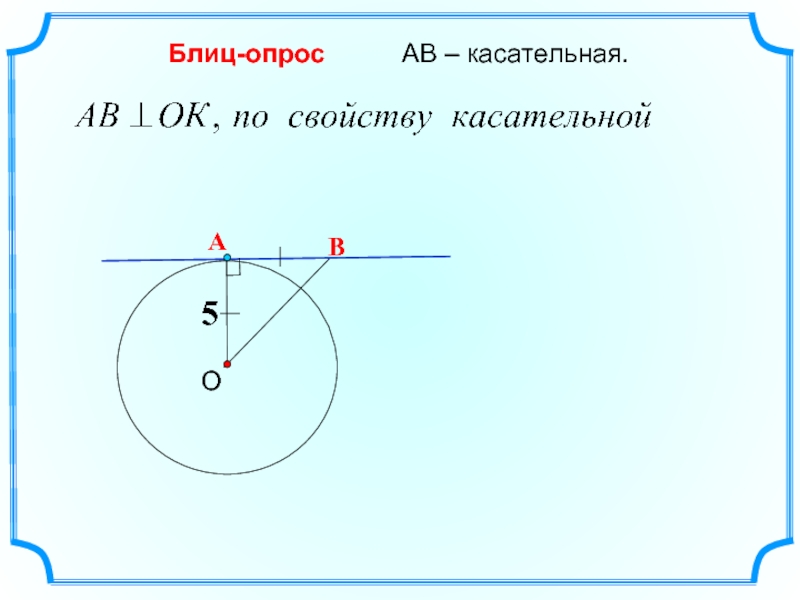
Свойство касательной.
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
А
В
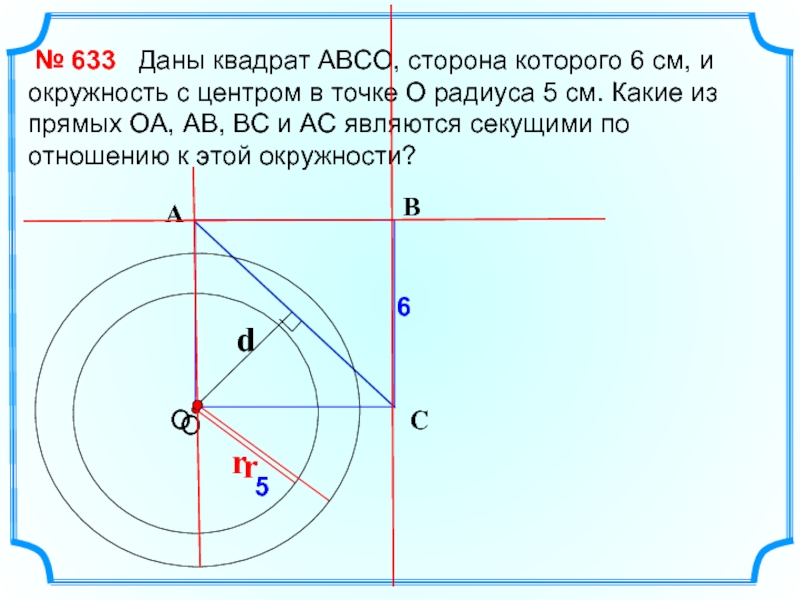
Слайд 6
Даны квадрат АВСО,
сторона которого 6 см, и
окружность с центром в точке О радиуса 5 см. Какие из прямых ОА, АВ, ВС и АС являются секущими по отношению к этой окружности?
окружность с центром в точке О радиуса 5 см. Какие из прямых ОА, АВ, ВС и АС являются секущими по отношению к этой окружности?
А
В
С
№ 633
5
6
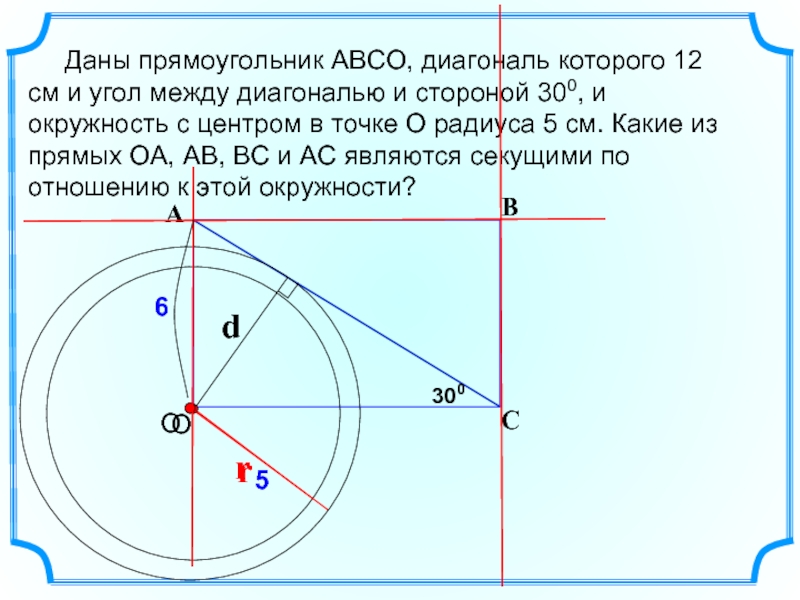
Слайд 7
Даны прямоугольник АВСО, диагональ которого 12 см и
угол между диагональю и стороной 300, и окружность с центром в точке О радиуса 5 см. Какие из прямых ОА, АВ, ВС и АС являются секущими по отношению к этой окружности?
А
В
С
5
6
300
Слайд 8 Радиус ОМ окружности
с центром О делит хорду АВ пополам. Докажите, что касательная, проведенная через точку М, параллельна хорде АВ.
№ 634
F
Слайд 9
600
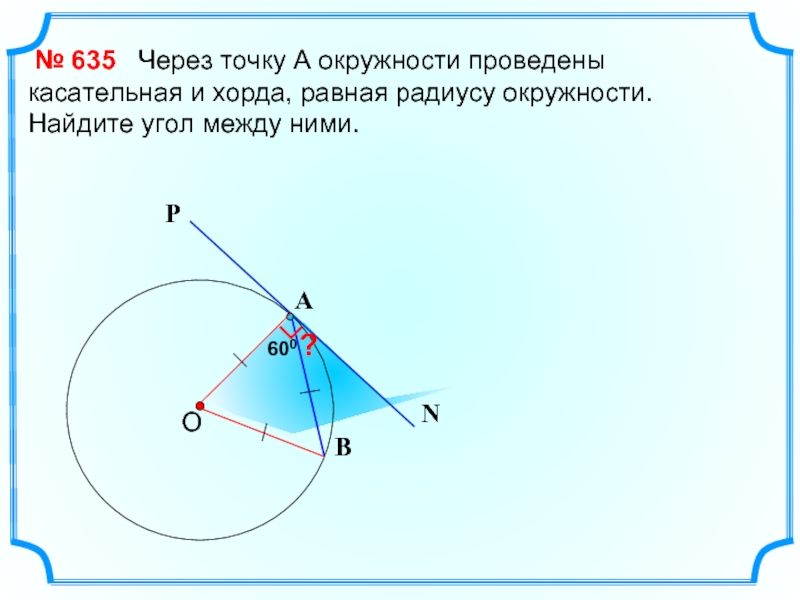
Через точку А
окружности проведены касательная и хорда, равная радиусу окружности. Найдите угол между ними.
№ 635
?
Слайд 10600
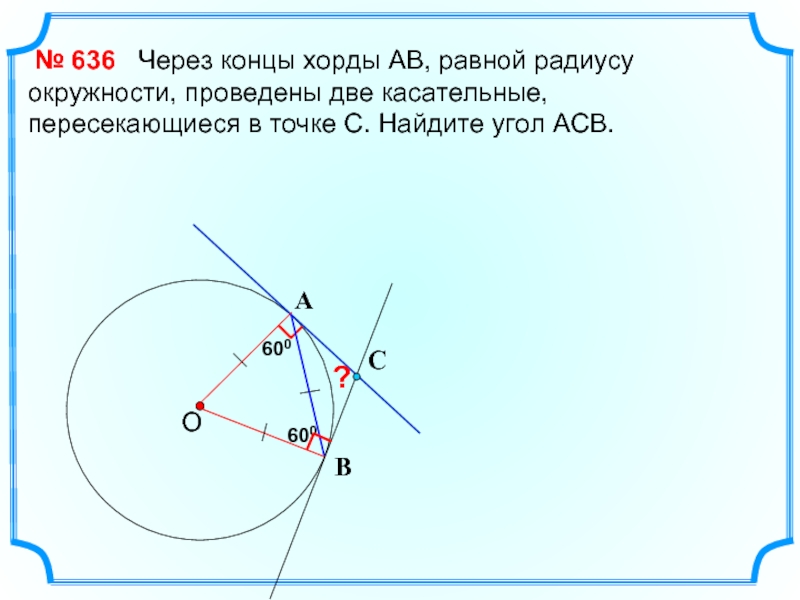
Через концы хорды
АВ, равной радиусу окружности, проведены две касательные, пересекающиеся в точке С. Найдите угол АСВ.
№ 636
?
600
Слайд 11
300
Угол между диаметром АВ и хордой АС равен 300. Через точку С проведена касательная, пересекающая прямую АВ в точке D. Докажите, что треугольник АСD равнобедренный.
№ 637 дом.
300
Слайд 12
Отрезки касательных к окружности, проведенные из одной точки равны и составляют
равные углы с прямой, проходящей через эту точку и центр окружности.
Свойство отрезков касательных
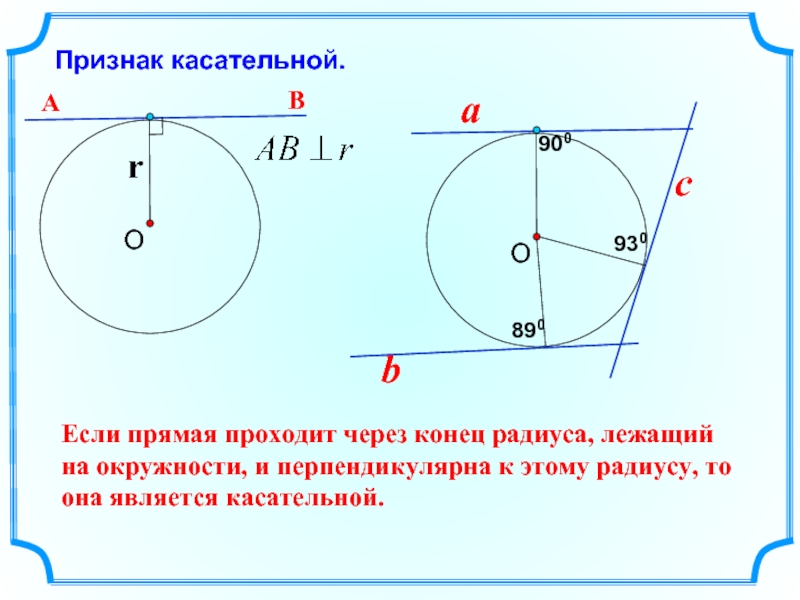
Слайд 13Признак касательной.
О
r
Если прямая проходит через конец радиуса, лежащий на окружности, и
перпендикулярна к этому радиусу, то она является касательной.
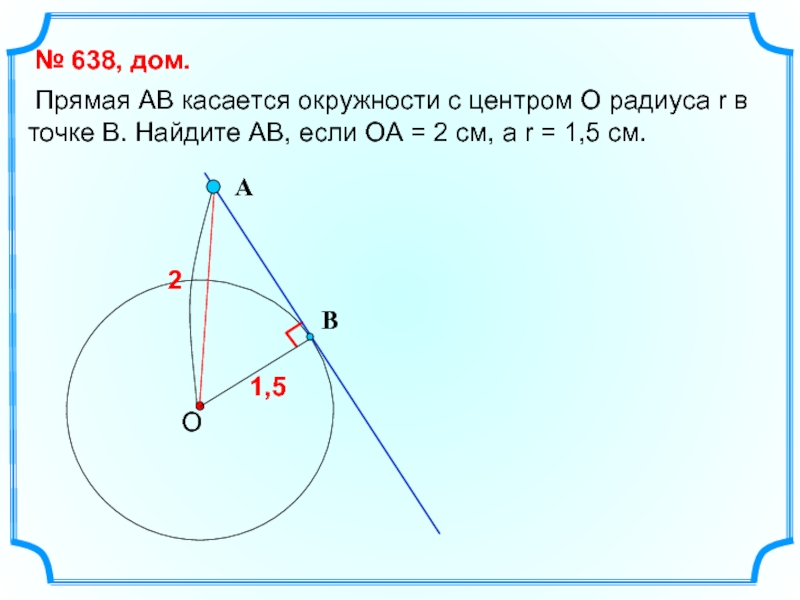
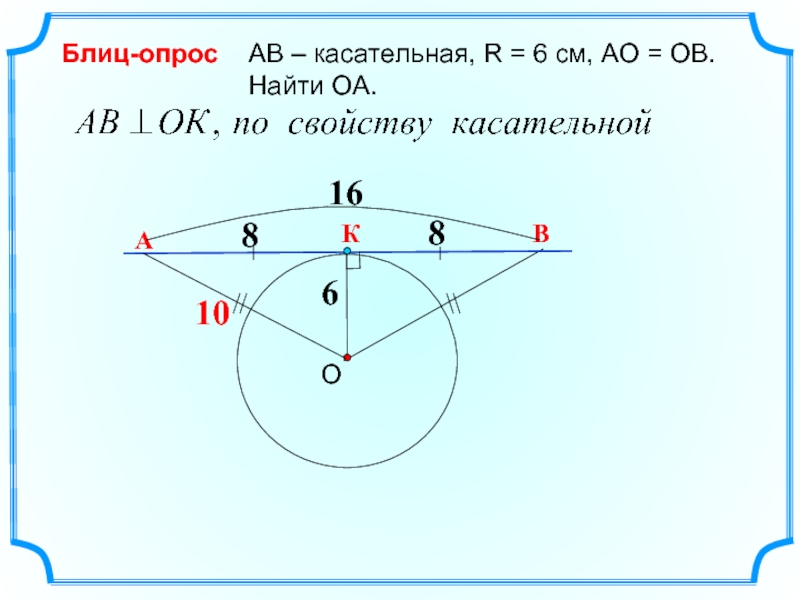
Слайд 14 Прямая АВ касается окружности с центром О радиуса r в
точке В. Найдите АВ, если ОА = 2 см, а r = 1,5 см.
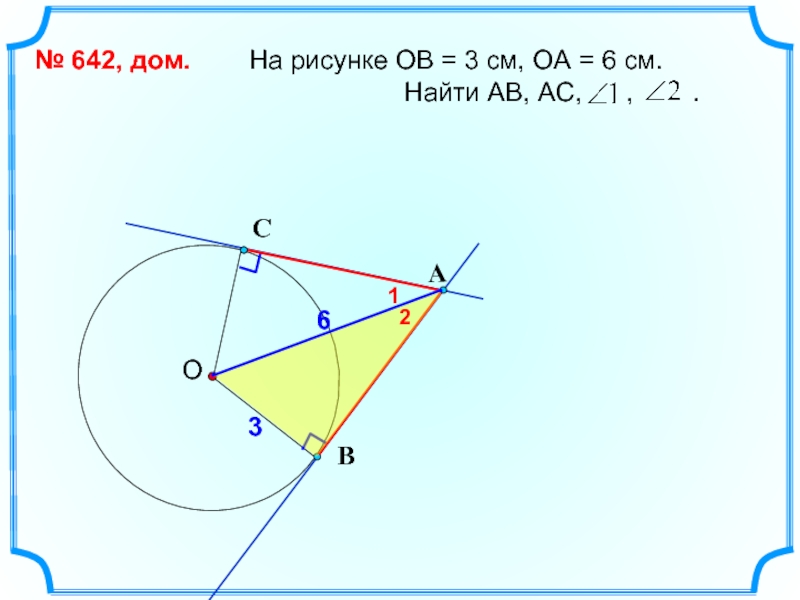
№ 638, дом.
1,5
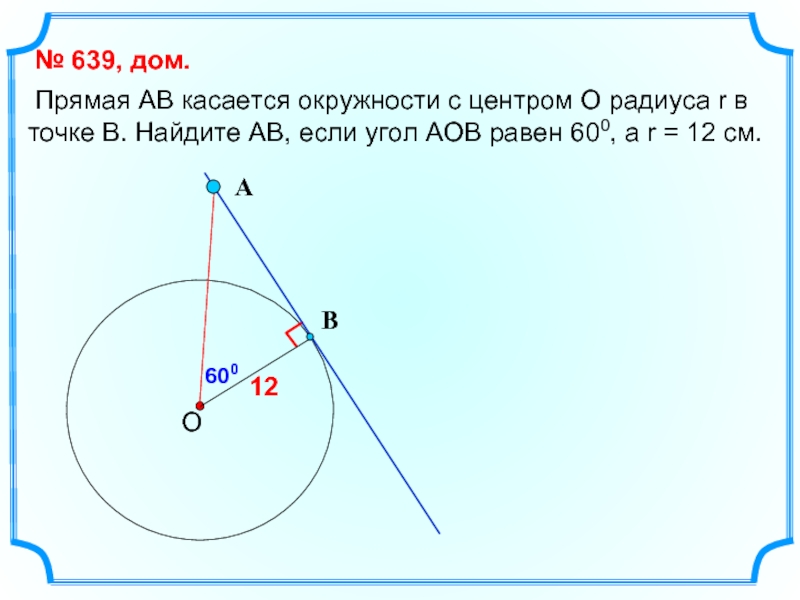
Слайд 15 Прямая АВ касается окружности с центром О радиуса r в
точке В. Найдите АВ, если угол АОВ равен 600, а r = 12 см.
№ 639, дом.
12
600
Слайд 194
В
О
М, N, K – точки касания. Найти РАВС.
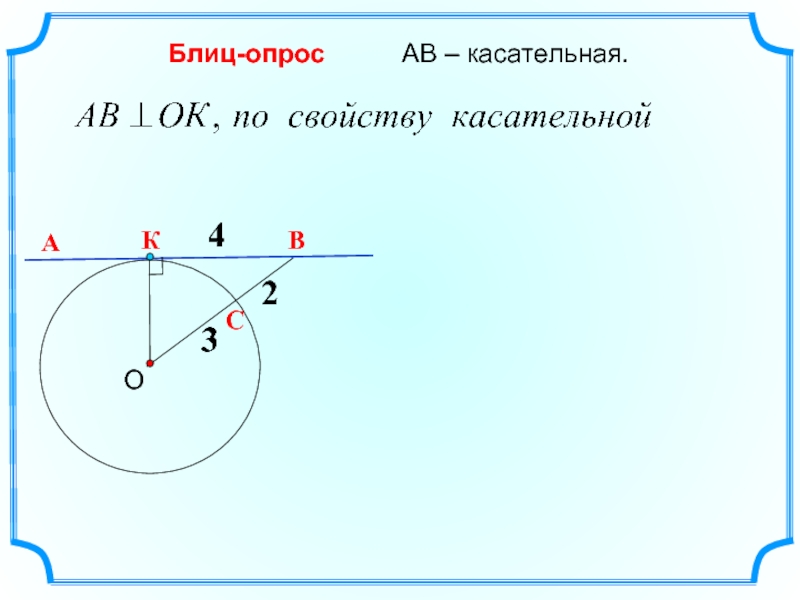
Блиц-опрос
А
4
С
М
N
K
5
8
5
8
ВМ = ВN
CK = CN
AM = AK
отрезки касательных
Слайд 21
Даны окружность с центром О радиуса
4,5 см и точка А. Через точку А проведены две касательные к окружности. Найдите угол между ними, если ОА=9см.
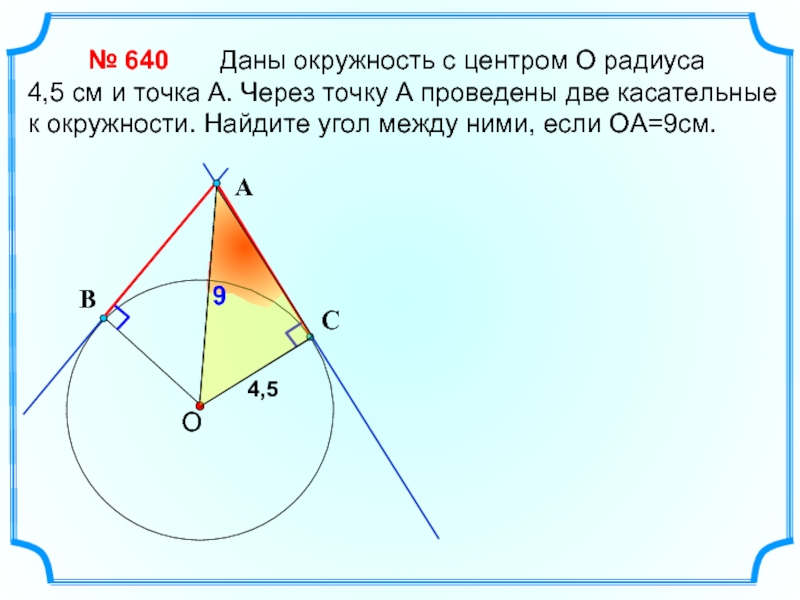
4,5 см и точка А. Через точку А проведены две касательные к окружности. Найдите угол между ними, если ОА=9см.
№ 640
Слайд 22
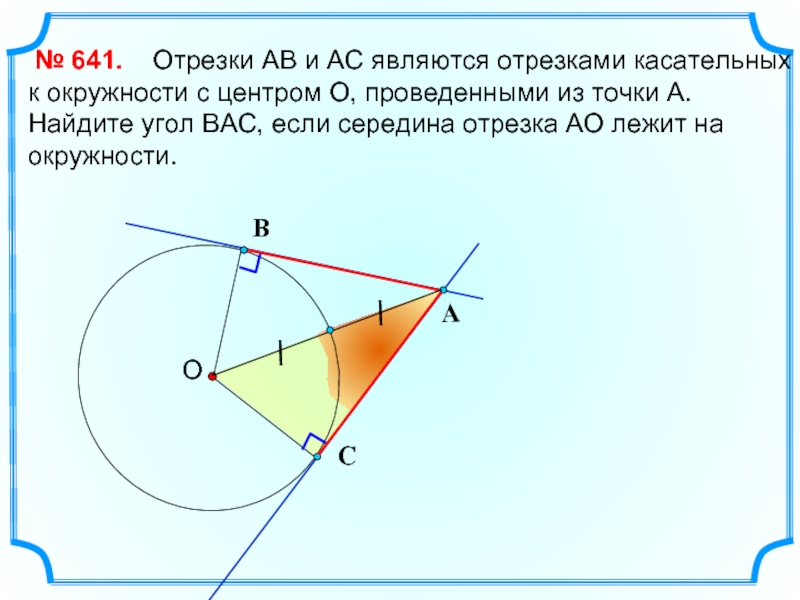
Отрезки АВ
и АС являются отрезками касательных к окружности с центром О, проведенными из точки А. Найдите угол ВАС, если середина отрезка АО лежит на окружности.
№ 641.
О
А
Слайд 23
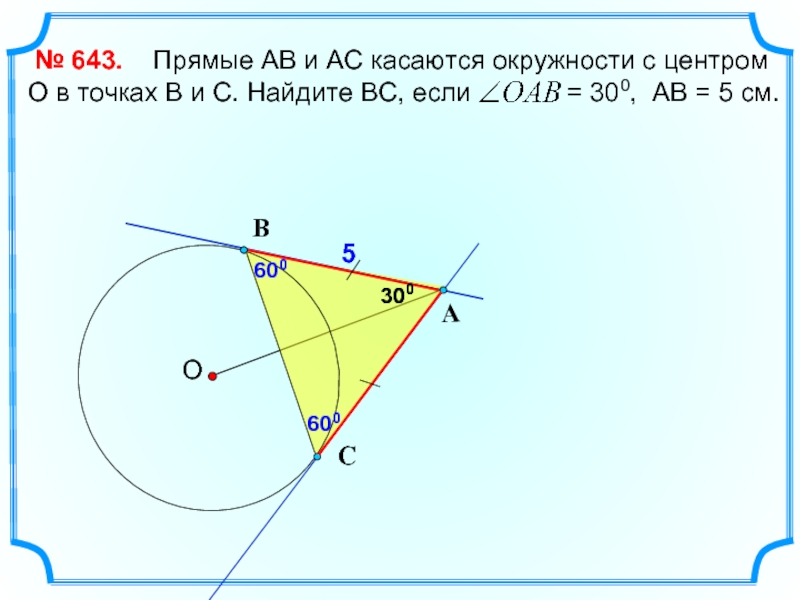
Прямые АВ
и АС касаются окружности с центром О в точках В и С. Найдите ВС, если = 300, АВ = 5 см.
№ 643.
О
А
5
300
300
