- выпуклость функции на промежутке - точки перегиба - асимптоты - построение графика функции }
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Исследование и построение графиков функции презентация
Содержание
- 1. Исследование и построение графиков функции
- 2. Интервалы возрастания и убывания функции Интервалы монотонного
- 3. Выпуклость функции на промежутке
- 4. Выпуклость функции на промежутке
- 5. Точки перегиба x0 Точку M(x0
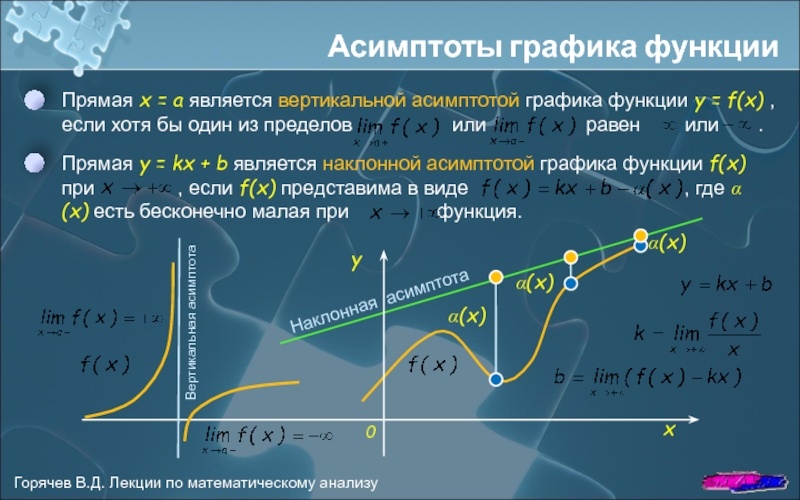
- 6. Асимптоты графика функции Вертикальная асимптота Наклонная асимптота
- 7. Построение графика функции Для построения рекомендуется следующая
- 8. Пример построения графика функции Исследуем и строим
- 9. Пример построения графика функции Найти нули функции, наклонные (горизонтальные) асимптоты. 0
- 10. Пример построения графика функции 0
- 11. Пример построения графика функции Найти
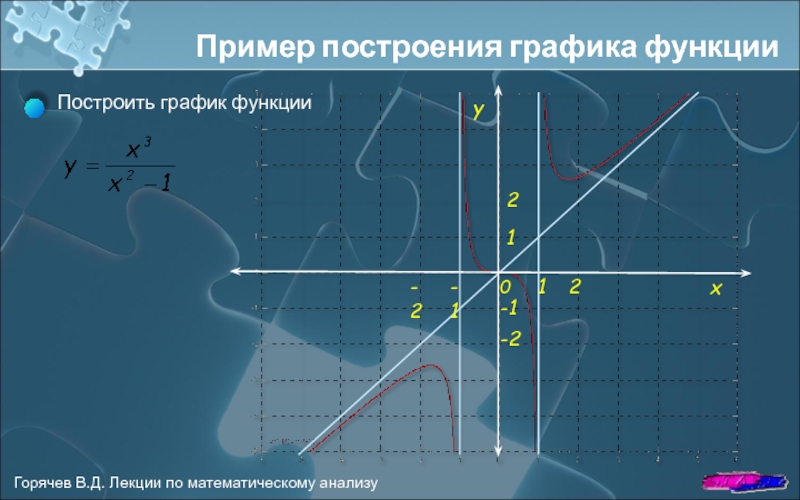
- 12. Пример построения графика функции Построить график функции
Интервалы возрастания и убывания функции Интервалы монотонного возрастания и убывания функции определяются знаком производной.
Слайд 1ИССЛЕДОВАНИЕ И ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИИ
{ интервалы монотонного возрастания и убывания функции
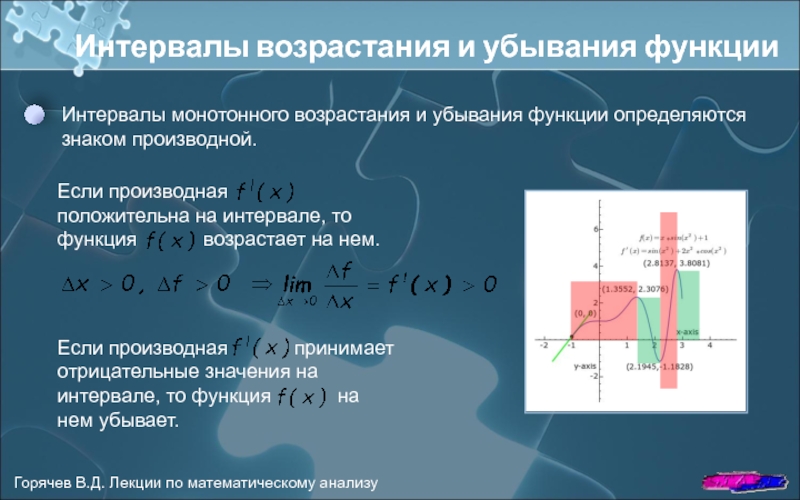
Слайд 2Интервалы возрастания и убывания функции
Интервалы монотонного возрастания и убывания функции определяются
знаком производной.
Слайд 5Точки перегиба
x0
Точку M(x0 ;f(x0)) кривой y = f(x) называют её точкой
перегиба, если она отделяет участок графика, где он выпуклый, от участка, где график функции f(x) вогнут.
Слайд 7Построение графика функции
Для построения рекомендуется следующая последовательность действий.
Найти множество определения
функции, области непрерывности, точки разрыва.
Найти асимптоты графика функции.
Найти точки пересечения графика с осями координат.
Найти первую и, если нужно, вторую производную функции. Найти точки в которых первая и вторая производные либо не существуют, либо обращаются в нуль.
Составить таблицу изменения знака функции, первой и второй производных. Определить промежутки возрастания и убывания функции, выпуклости и вогнутости функции, найти точки экстремума и точки перегиба, вычислить значения функции в этих точках.
При построении графика учитывать такие свойства, как четность, нечетность, периодичность.
Окончательно вычертить график функции.
Слайд 8Пример построения графика функции
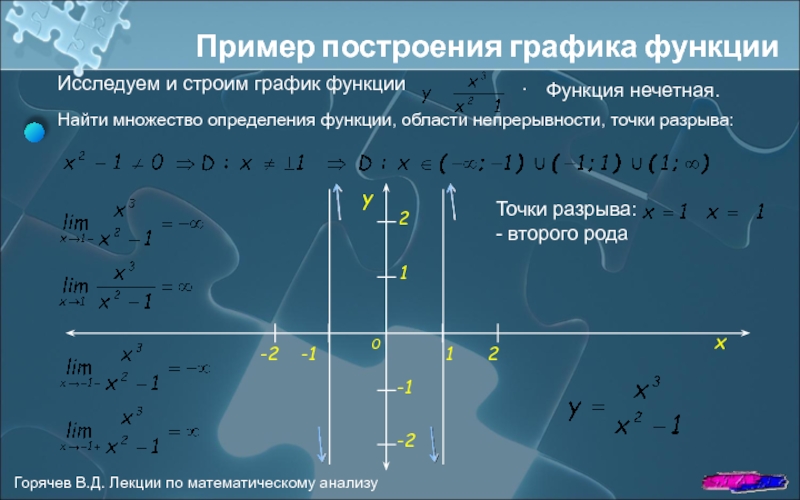
Исследуем и строим график функции
.
Найти множество определения функции, области непрерывности, точки разрыва:
Функция нечетная.
Слайд 10Пример построения графика функции
0
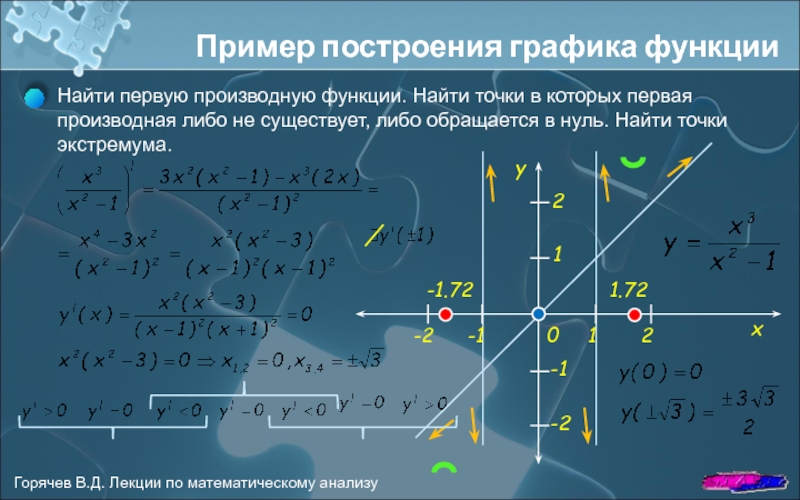
Найти первую производную функции. Найти точки в которых
первая производная либо не существует, либо обращается в нуль. Найти точки экстремума.
-1.72
1.72
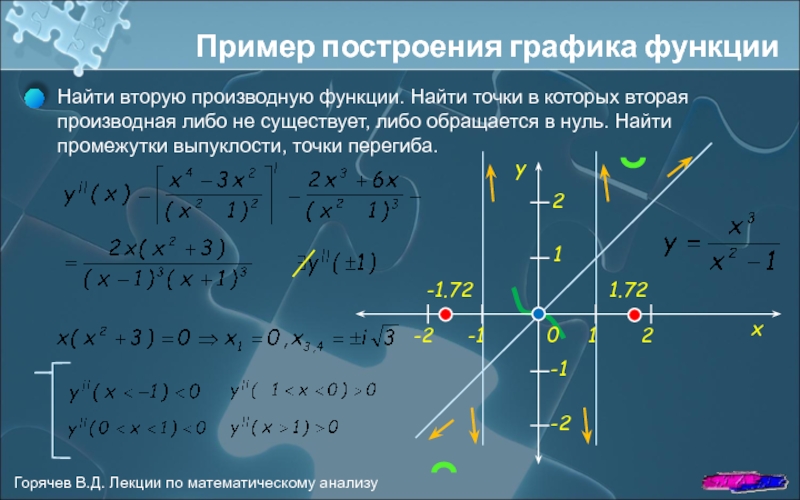
Слайд 11
Пример построения графика функции
Найти вторую производную функции. Найти точки в которых
вторая производная либо не существует, либо обращается в нуль. Найти промежутки выпуклости, точки перегиба.
