- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Independent samples using the test statistic презентация
Содержание
- 1. Independent samples using the test statistic
- 2. Section 8-3 Testing the Difference Between Means
- 3. Steps to Using the t-Test for the
- 4.
- 5. Example 1 on page 463— A golf
- 6.
- 7. Example 1 on page 463— 2nd VARS
- 8. Example 1 on page 463— Step 6: Determine
- 9.
- 10. Example 2 (Page 465) A state legislator
- 11.
- 12. Example 2 (Page 465) 2nd VARS 4
- 13. Example 2 (Page 465) Step 6: Determine the
- 14.
- 15. Assignments: Classwork: Page 466 #1-8 All Homework: Pages 466-469 #10-20 Evens
Слайд 2Section 8-3
Testing the Difference Between Means (Dependent Samples)
We can conduct the
hypothesis test on two dependent samples if ALL of the following conditions are met:
1) The samples must be randomly selected.
2) The samples must be dependent (paired).
3) Both populations must be normally distributed.
If all of these conditions are met, we will use a t-distribution with n – 1 degrees of freedom (n is the number of data pairs).
1) The samples must be randomly selected.
2) The samples must be dependent (paired).
3) Both populations must be normally distributed.
If all of these conditions are met, we will use a t-distribution with n – 1 degrees of freedom (n is the number of data pairs).
Слайд 3Steps to Using the t-Test for the Difference Between Means (Dependent
Samples)
State H0 and Ha.
Identify α
Identify the degrees of freedom (d.f. = n-1)
Determine the critical value Use the t-distribution chart OR InvT function on the calculator
Determine the rejection region To the left, right, or both sides of the critical value.
Find the differences between data pairs
STAT Edit, L1 and L2, highlight L3; type in L1-L2
State H0 and Ha.
Identify α
Identify the degrees of freedom (d.f. = n-1)
Determine the critical value Use the t-distribution chart OR InvT function on the calculator
Determine the rejection region To the left, right, or both sides of the critical value.
Find the differences between data pairs
STAT Edit, L1 and L2, highlight L3; type in L1-L2
Слайд 5Example 1 on page 463—
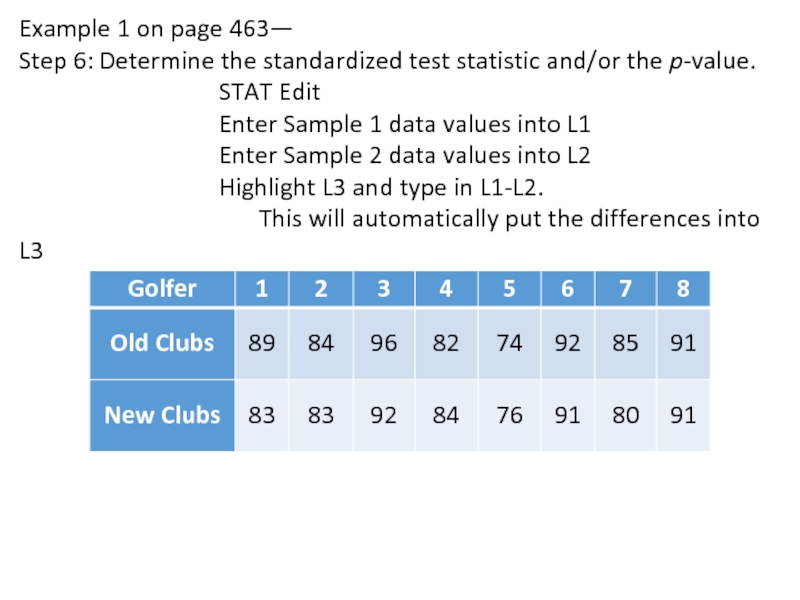
A golf club manufacturer claims that golfers
can lower their scores by using the manufacturer’s newly designed golf clubs. Eight golfers are randomly selected, and each is asked to give his or her most recent score. After using the new clubs for one month, the golfers are again asked to give their most recent score. The scores for each golfer are shown in a table below. Assuming the golf scores are normally distributed, is there enough evidence to support the manufacturer’s claim at α = 0.10?
Слайд 7Example 1 on page 463—
2nd VARS 4
Enter 1 - α for
right tail test and 7 for df .
Calculate
1.415 (same as the chart!!)
Step 5: Determine the rejection region:
The rejection region is t > 1.415.
Calculate
1.415 (same as the chart!!)
Step 5: Determine the rejection region:
The rejection region is t > 1.415.
Слайд 8Example 1 on page 463—
Step 6: Determine the standardized test statistic and/or
the p-value.
STAT Edit
Enter Sample 1 data values into L1
Enter Sample 2 data values into L2
Highlight L3 and type in L1-L2.
This will automatically put the differences into L3
STAT Edit
Enter Sample 1 data values into L1
Enter Sample 2 data values into L2
Highlight L3 and type in L1-L2.
This will automatically put the differences into L3
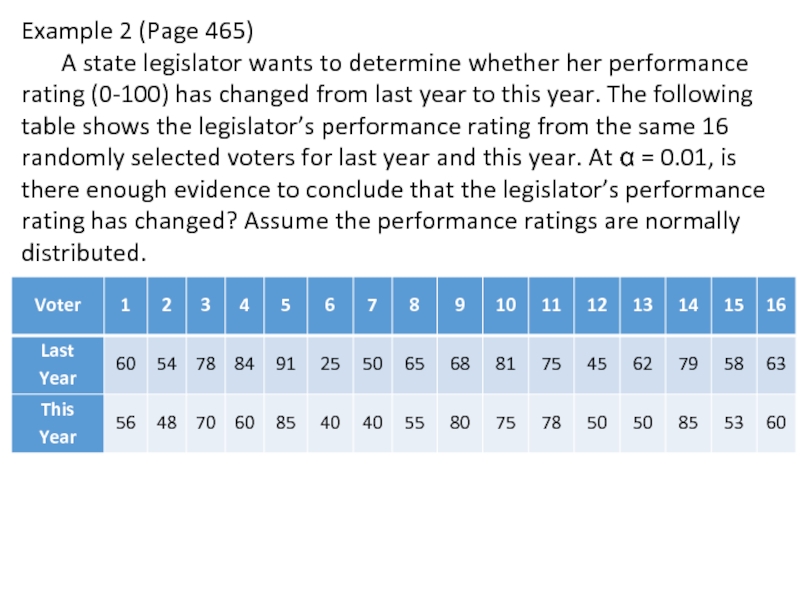
Слайд 10Example 2 (Page 465)
A state legislator wants to determine whether her
performance rating (0-100) has changed from last year to this year. The following table shows the legislator’s performance rating from the same 16 randomly selected voters for last year and this year. At α = 0.01, is there enough evidence to conclude that the legislator’s performance rating has changed? Assume the performance ratings are normally distributed.
Слайд 12Example 2 (Page 465)
2nd VARS 4
Enter α/2 for two tail test
and 15 for df .
Calculate
-2.947 (same as the chart!!)
Again, remember to use both the positive and the negative of the value given.
Step 5: Determine the rejection region:
The rejection region is t > 2.947 and t < -2.947.
Calculate
-2.947 (same as the chart!!)
Again, remember to use both the positive and the negative of the value given.
Step 5: Determine the rejection region:
The rejection region is t > 2.947 and t < -2.947.
Слайд 13Example 2 (Page 465)
Step 6: Determine the standardized test statistic and/or the
p-value.
STAT Edit
Enter Sample 1 data values into L1
Enter Sample 2 data values into L2
Highlight L3 and type in L1-L2.
This will automatically put the differences into L3.
STAT Edit
Enter Sample 1 data values into L1
Enter Sample 2 data values into L2
Highlight L3 and type in L1-L2.
This will automatically put the differences into L3.