- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Хвильові властивості світла презентация
Содержание
- 1. Хвильові властивості світла
- 2. ПЛАН 1. Основні закони геометричної оптики. 2.
- 3. На самостійну обробку: 1. Одержання когерентних хвиль
- 4. Основні закони геометричної оптики Геометрична оптика розглядає
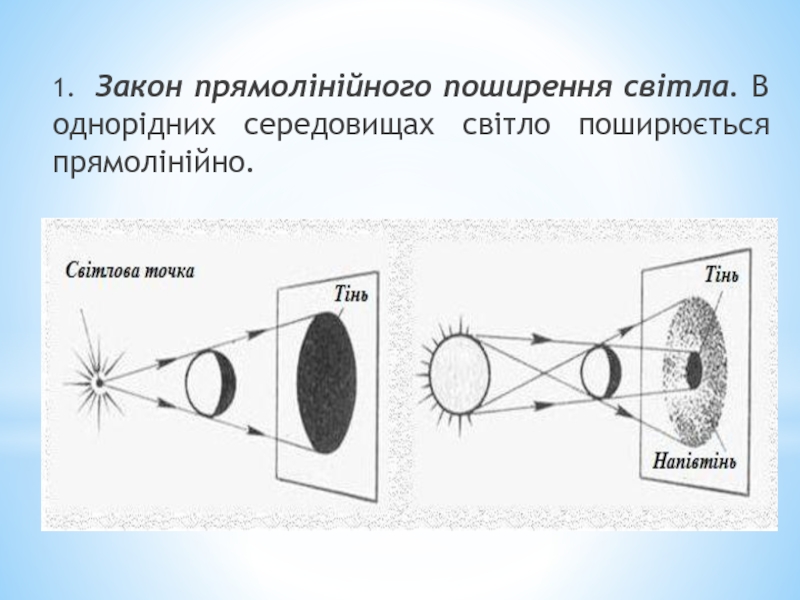
- 5. 1. Закон прямолінійного поширення світла. В однорідних середовищах світло поширюється прямолінійно.
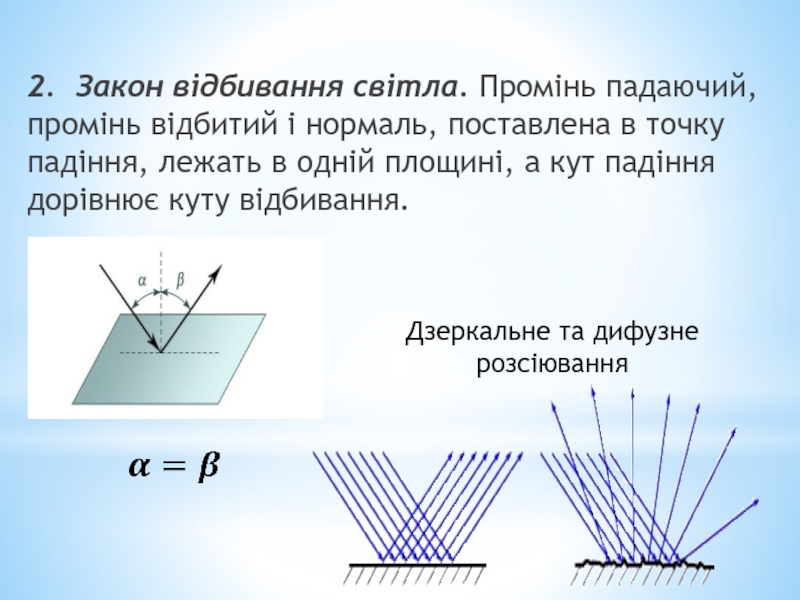
- 6. 2. Закон відбивання світла. Промінь падаючий,
- 7. 3. Закон заломлення світла (закон Снелліуса).
- 8. При переході світла з одного прозорого
- 9. 4. Закон незалежності поширення світлових променів.
- 10. 5. Закон оборотності (принцип оборотності) світлових
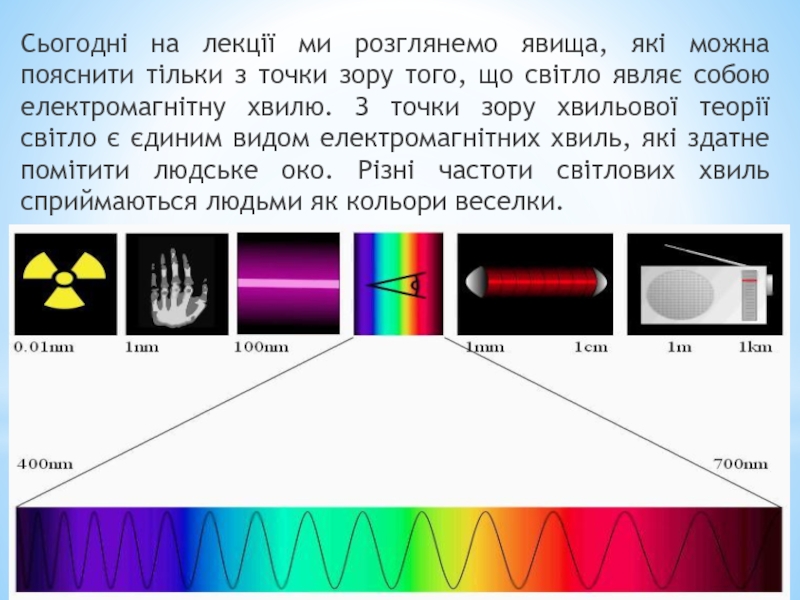
- 11. Сьогодні на лекції ми розглянемо явища,
- 12. Монохроматичність хвиль Монохроматична хвиля - це строго
- 13. Інтерференція хвиль На рисунку зображено хвилі, що
- 14. Інтерференція хвиль Отже, при додаванні у просторі
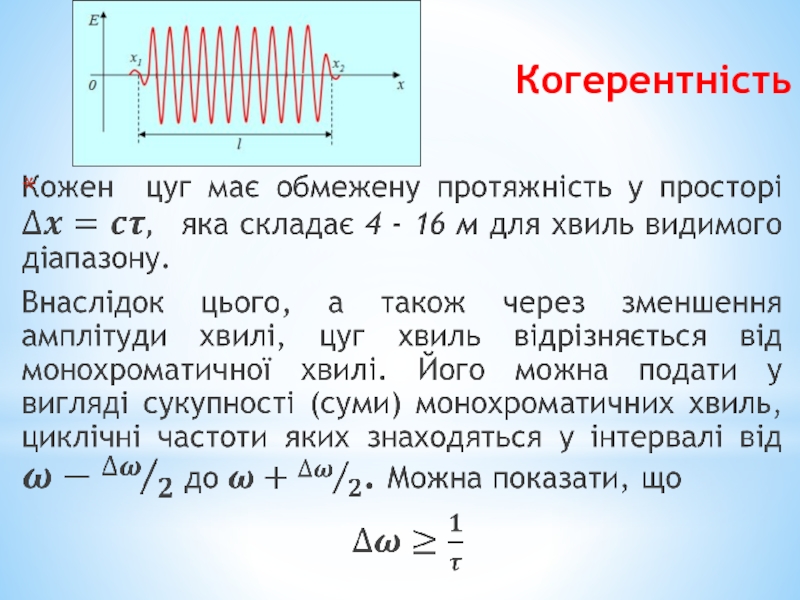
- 15. Когерентність
- 16. Когерентність
- 17. Когерентність
- 18. Когерентність
- 19. Когерентність
- 20. Просторова когерентність
- 21. Розрахунок інтерференції двох хвиль
- 22. Розрахунок інтерференції двох хвиль
- 23. Розрахунок інтерференції двох хвиль
- 24. Методи отримання когерентних хвиль Для отримання когерентних
- 25. Метод Юнга Джерелом світла є яскраво освітлена
- 26. Біпризма Френеля Складається з двох однакових призм,
- 27. Дзеркала Френеля
- 28. Оптична довжина шляху та різниця ходу
- 29. Оптична довжина шляху та різниця ходу
- 30. Оптична довжина шляху та різниця ходу
- 31. Утворення максимумів та мінімумів Максимум Мінімум
- 32. Дифракція - В загальному випадку під дифракцією
- 33. Принцип Гюйгенса-Френеля Природа та основні принципи дифракції
- 35. Метод зон Френеля Розрахунок інтерференції вторинних
- 36. Розрізняють два випадки дифракції : 1.
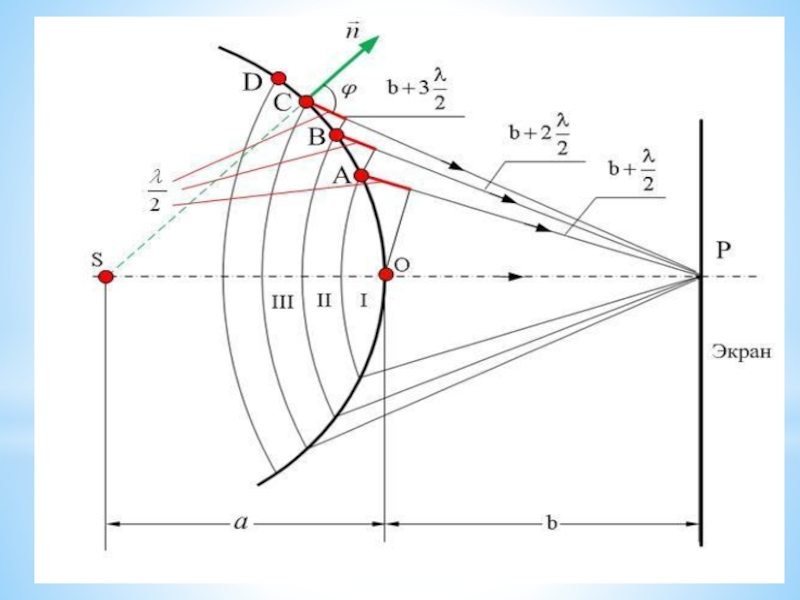
- 37. Дифракція Френеля на круглому отворі
- 39. Дифракція Френеля на круглому отворі
- 40. Дифракція Френеля на круглому отворі
- 41. Дифракція Френеля на круглому отворі
- 42. Дифракція Френеля на круглому отворі
- 43. Дифракція Френеля на круглому отворі
- 44.
- 45. Дифракція Френеля на невеликому диску (круглому непрозорому екрані)
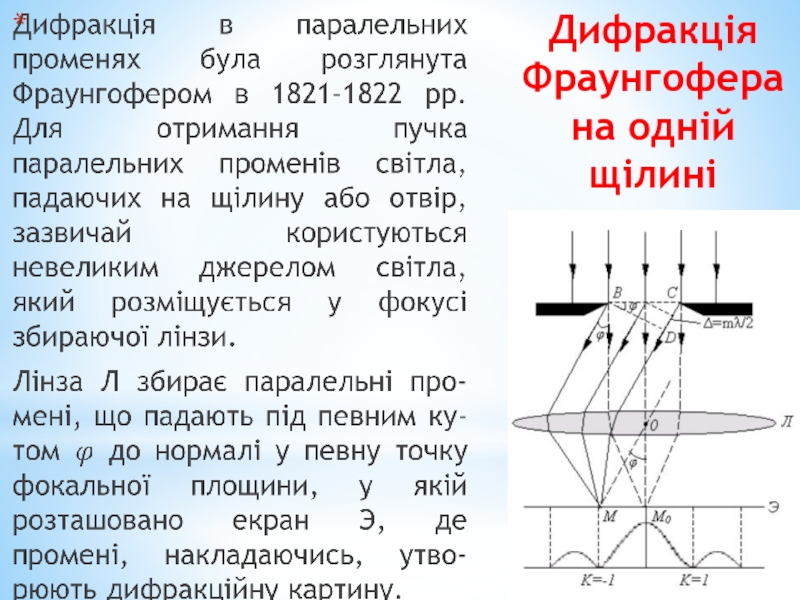
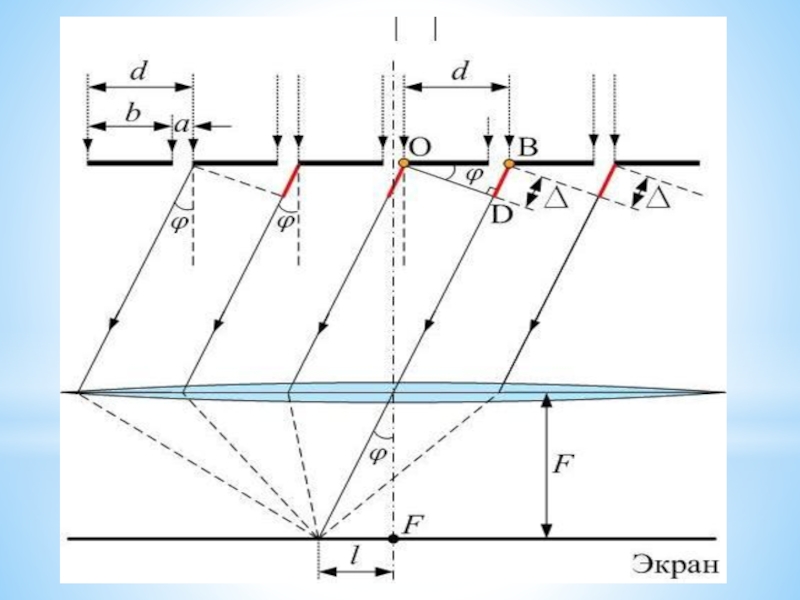
- 46. Дифракція Фраунгофера на одній щілині
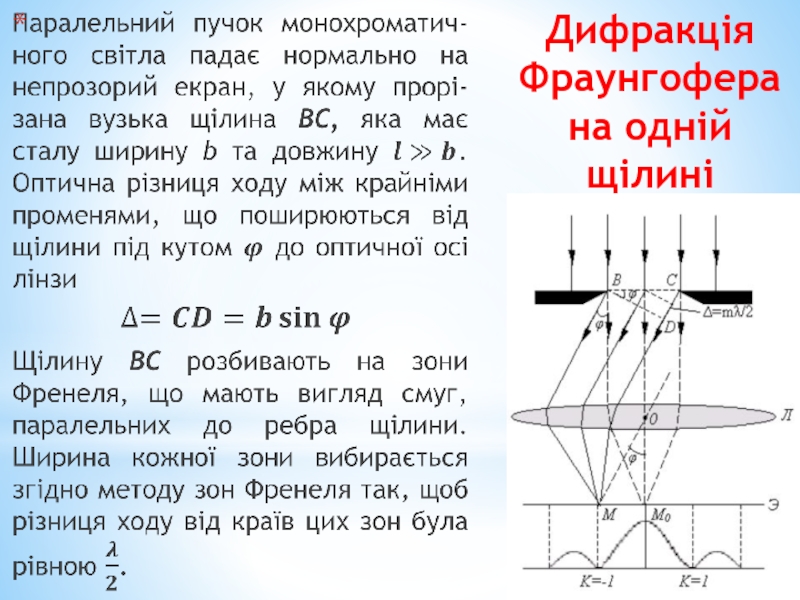
- 47. Дифракція Фраунгофера на одній щілині
- 48. Дифракція Фраунгофера на одній щілині
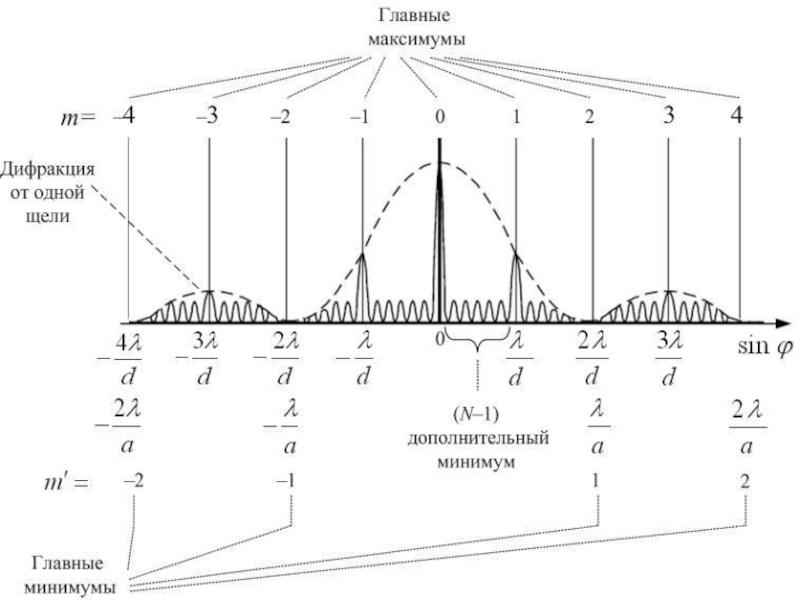
- 49. Розподіл інтенсивності на екрані, отриманий внаслідок
- 50. Кути, під якими спостерігаються максимуми усіх
- 51. Дифракційна гратка
- 53. Дифракційна гратка
- 54. Дифракційна гратка
- 56. Дифракційна гратка
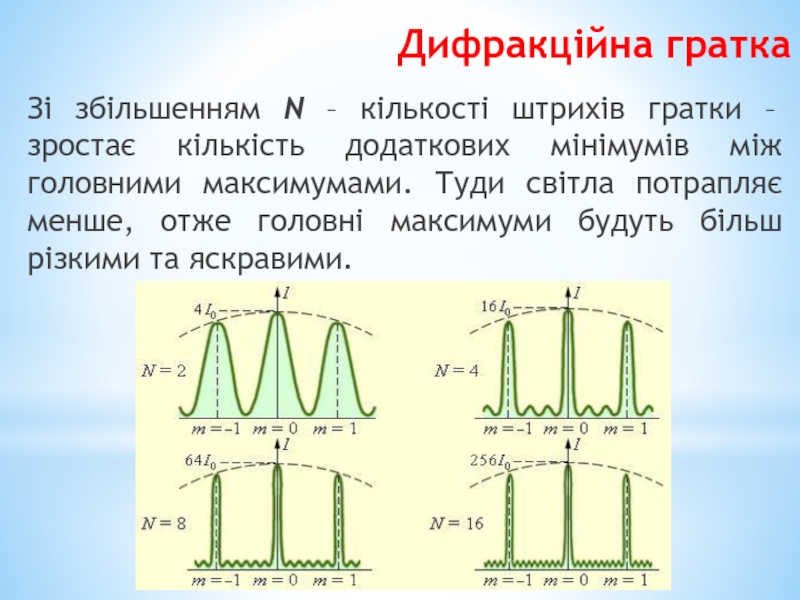
- 57. Дифракційна гратка Зі збільшенням N – кількості
- 58. ДЯКУЮ ЗА УВАГУ
Слайд 2ПЛАН
1. Основні закони геометричної оптики.
2. Монохроматичні хвилі. Інтерференція хвиль.
3. Когерентність
4. Розрахунок інтерференції двох хвиль.
5. Метод отримання когерентних хвиль (Юнга та Френеля).
6. Дифракція хвиль. Принцип Гюйгенса-Френеля.
7. Метод зон Френеля. Дифракція Фраунгофера на щілині.
8. Дифракційна гратка.
Слайд 3На самостійну обробку:
1. Одержання когерентних хвиль методом поділу амплітуди. Смуги рівного
2. Інтерференція світла у тонких плівках. Просвітлення оптики.
3. Дифракція на просторовій кристалічній гратці. Рівняння Вульфа-Брегга.
4. Роздільна здатність оптичних приладів. Поняття про голографію.
Слайд 4Основні закони геометричної оптики
Геометрична оптика розглядає закони поширення світла в прозорих
В основі геометричної оптики лежать наступні закони.
Слайд 5
1. Закон прямолінійного поширення світла. В однорідних середовищах світло поширюється прямолінійно.
Слайд 6
2. Закон відбивання світла. Промінь падаючий, промінь відбитий і нормаль, поставлена
Дзеркальне та дифузне розсіювання
Слайд 7
3. Закон заломлення світла (закон Снелліуса). Промінь падаючий, промінь заломлений і
Слайд 8
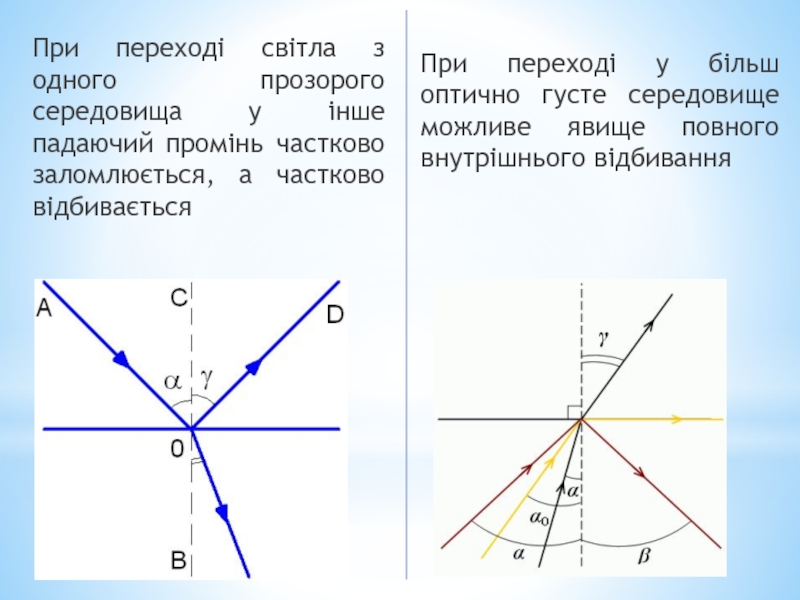
При переході світла з одного прозорого середовища у інше падаючий промінь
При переході у більш оптично густе середовище можливе явище повного внутрішнього відбивання
Слайд 9
4. Закон незалежності поширення світлових променів. Світлові промені, поширюючись у просторі,
Слайд 10
5. Закон оборотності (принцип оборотності) світлових променів. Якщо промінь падає з
Слайд 11
Сьогодні на лекції ми розглянемо явища, які можна пояснити тільки з
Слайд 12Монохроматичність хвиль
Монохроматична хвиля - це строго гармонічна хвиля з постійними у часі частотою,
Амплітуда та фаза такої хвилі можуть змінюватися від однієї точки простору до іншої, частота ж залишається сталою у всьому просторі.
Монохроматичні хвилі не обмежені ні в часі, ні у просторі, тобто не мають початку і кінця. Тому вони не можуть бути реалізовані у дійсності(ідеальні). Проте ця ідеалізація має величезне значення у вченні про хвилі.
Слайд 13Інтерференція хвиль
На рисунку зображено хвилі, що збуджуються на поверхні води двома
Якщо гребінь однієї хвилі співпадає з гребнем іншої, то у цій точці коливання посилюють одне одного, а якщо гребінь однієї співпадає з западиною іншої – хвилі одна одну гасять.
Слайд 14Інтерференція хвиль
Отже, при додаванні у просторі двох або декількох хвиль можуть
Це явище називається інтерференцією хвиль.
Утворена картина буде стійкою (зберігатиметься у часі) при накладанні когерентних хвиль (хвиль, що випромінюються когерентними джерелами).
Слайд 24Методи отримання когерентних хвиль
Для отримання когерентних світлових хвиль за допомогою звичайних
Розділення світла на когерентні пучки можна здійснити за допомогою екранів та щілин, дзеркал та заломлюючих тіл.
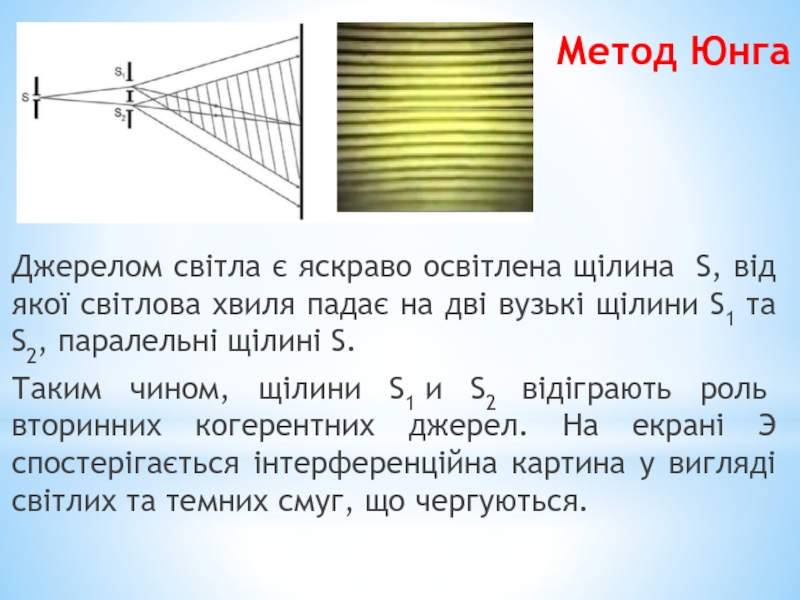
Слайд 25Метод Юнга
Джерелом світла є яскраво освітлена щілина S, від якої світлова
Таким чином, щілини S1 и S2 відіграють роль вторинних когерентних джерел. На екрані Э спостерігається інтерференційна картина у вигляді світлих та темних смуг, що чергуються.
Слайд 26Біпризма Френеля
Складається з двох однакових призм, що складені основами. Світло від
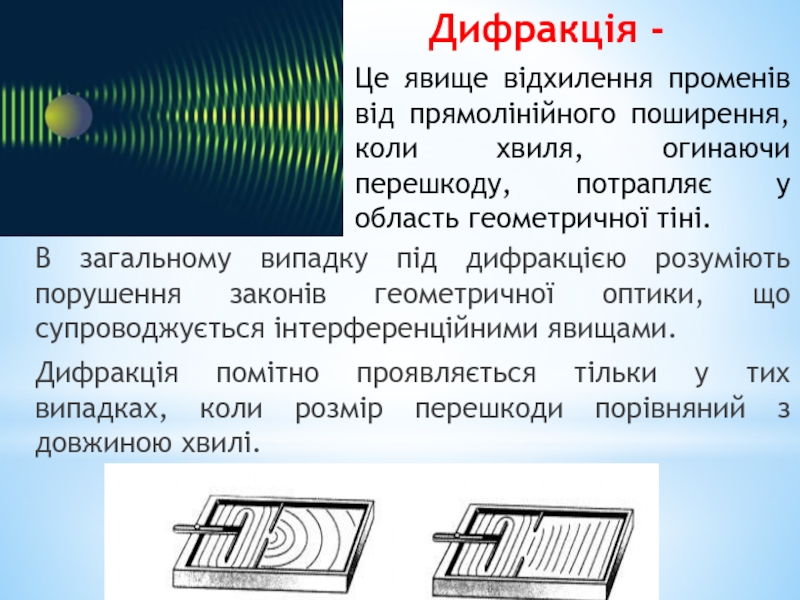
Слайд 32Дифракція -
В загальному випадку під дифракцією розуміють порушення законів геометричної оптики,
Дифракція помітно проявляється тільки у тих випадках, коли розмір перешкоди порівняний з довжиною хвилі.
Це явище відхилення променів від прямолінійного поширення, коли хвиля, огинаючи перешкоду, потрапляє у область геометричної тіні.
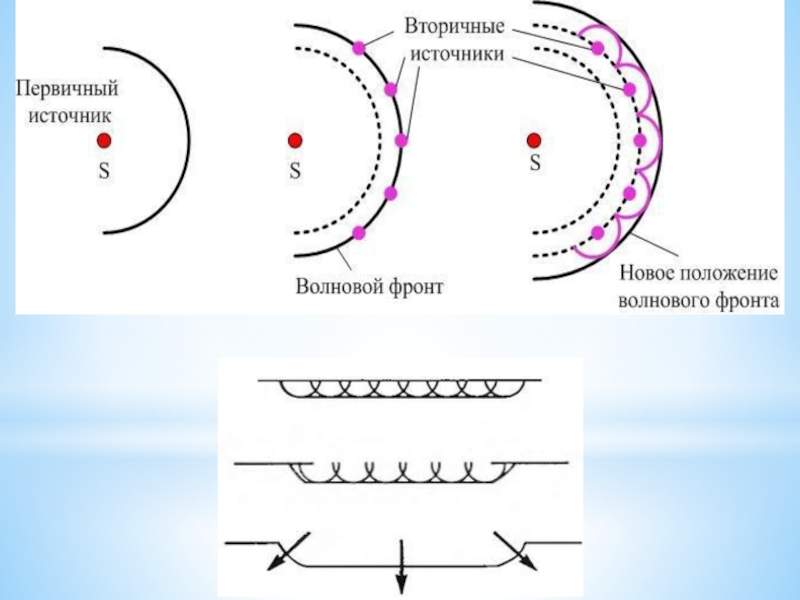
Слайд 33Принцип Гюйгенса-Френеля
Природа та основні принципи дифракції можна встановити за допомогою принципу
У 1678 р. Гюйгенс сформулював правило, назване принципом Гюйгенса: кожна точка, до якої дійшла хвиля, стає джерелом (центром) вторинної хвилі, а огинаюча вторинних хвиль задає положення хвильового фронту у наступний момент часу.
Недолік принципу Гюйгенса полягає у тому, що він не враховує явище інтерференції вторинних хвиль і як наслідок цього не дозволяє розрахувати амплітуди хвиль, які поширюються у різних напрямках.
Цей недолік усунув Френель, який у 1815 р. доповнив принцип Гюйгенса, ввівши уявлення про когерентність вторинних хвиль та про їх інтерференцію. Доповнений Френелем принцип Гюйгенса називається принципом Гюйгенса-Френеля.
Слайд 35Метод зон Френеля
Розрахунок інтерференції вторинних хвиль зводиться до інтегрування, яке часто
Для спрощення обчислень при визначенні амплітуди хвилі в заданій точці простору Френель запропонував розбити поверхню фронту хвилі на зони (зони Френеля) таким чином, щоб хвилі від сусідніх зон приходили у точку спостереження у протифазі і таким чином послаблювали одна одну.
Застосуємо метод зон Френеля для розрахунку дифракції світла.
Слайд 36
Розрізняють два випадки дифракції :
1. Дифракція Френеля або дифракція у променях,
2. Дифракція Фраунгофера або дифракція у параллельних променях, коли на перешкоду падає плоска хвиля, а дифракційна картина спостерігається на екрані, який знаходиться у фокальній площині збиральної лінзи, встановленої на шляху світла, що пройшло через перешкоду.