- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Графы. Основные определения презентация
Содержание
- 1. Графы. Основные определения
- 2. Задача о Кёнигсбергских мостах. Обойти все
- 3. Задача о трех домах и трех колодцах.
- 4. Задача о четырех красках. Любую карту на
- 5. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ Графом G (V
- 6. Обычно граф изображают диаграммой: вершины —
- 7. Пусть v1, v2 — вершины,
- 9. Если элементами множества Е являются упорядоченные пары,
- 10. Если бинарное отношение Е является симметричным, то
- 11. Если элементом множества Е может быть пара
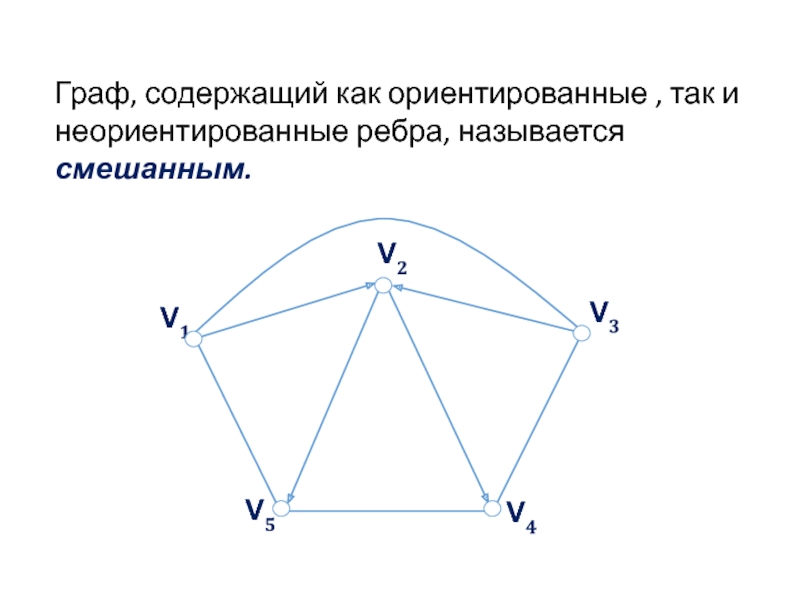
- 12. Граф, содержащий как ориентированные , так и неориентированные ребра, называется смешанным.
- 13. Если Е является не множеством, а набором,
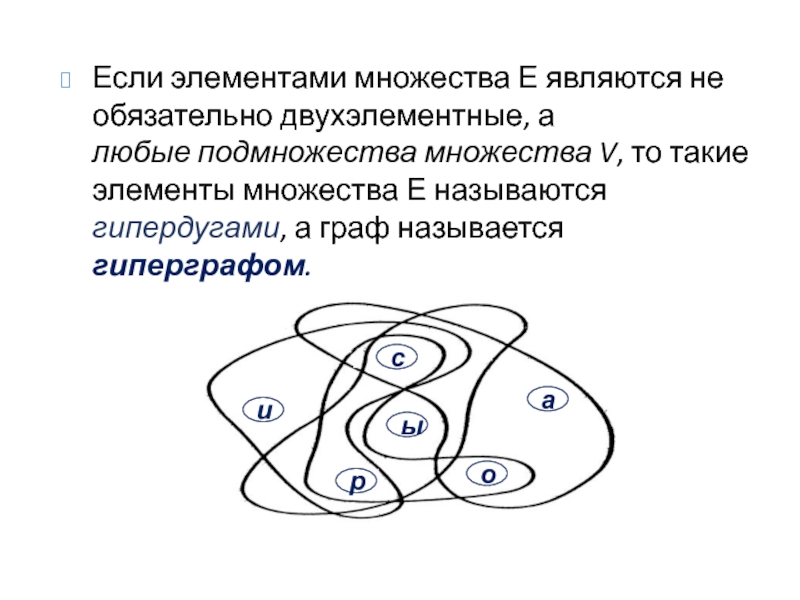
- 14. Если элементами множества Е являются не обязательно
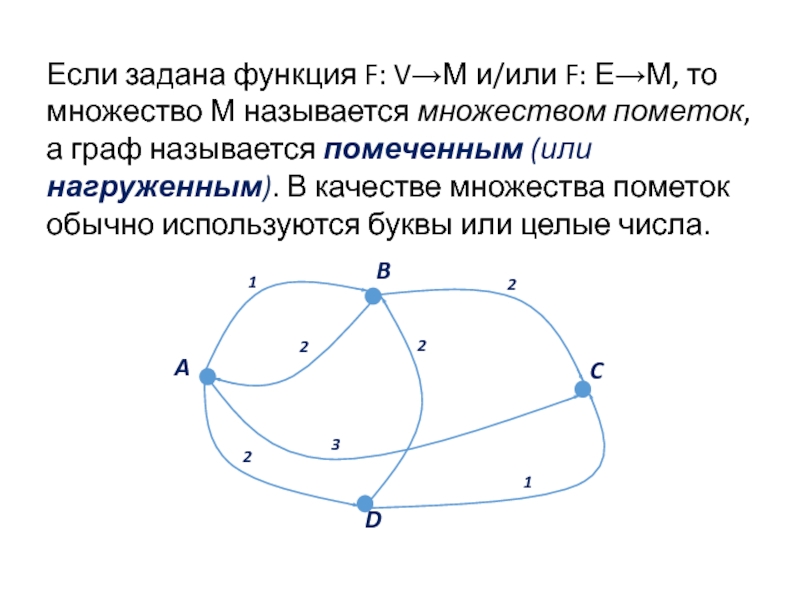
- 15. Если задана функция F: V→М и/или F:
- 16. Способы задания графа
- 17. Пусть G= (М, R) - граф, в
- 18.
- 19. Если Aij = 1, то вершина aj
- 20. Матрица инцидентности Если число вершин
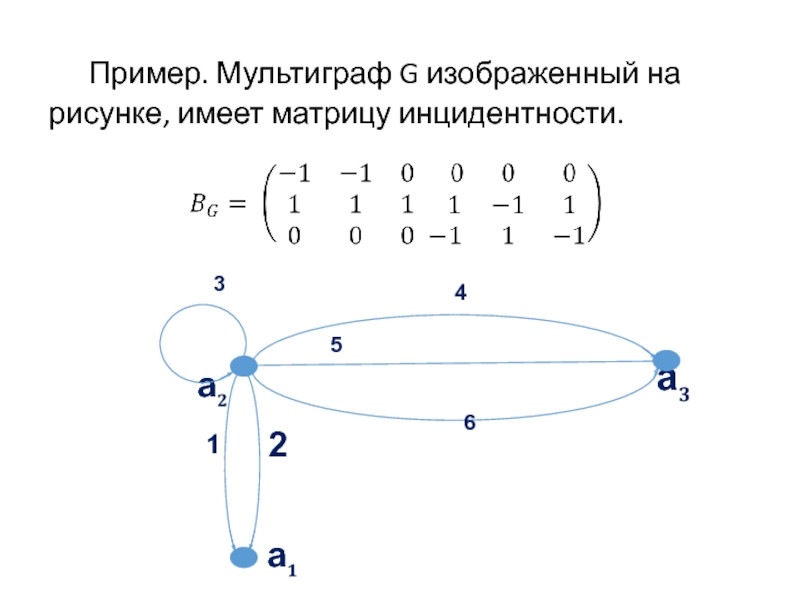
- 21. Пример. Мультиграф G изображенный на рисунке, имеет матрицу инцидентности.
- 22. 681
- 23. Информацию о весах дуг во взвешенном графе
- 24. Операции над графами
- 25. Граф G'(V’, E') называется подграфом графа G(V,
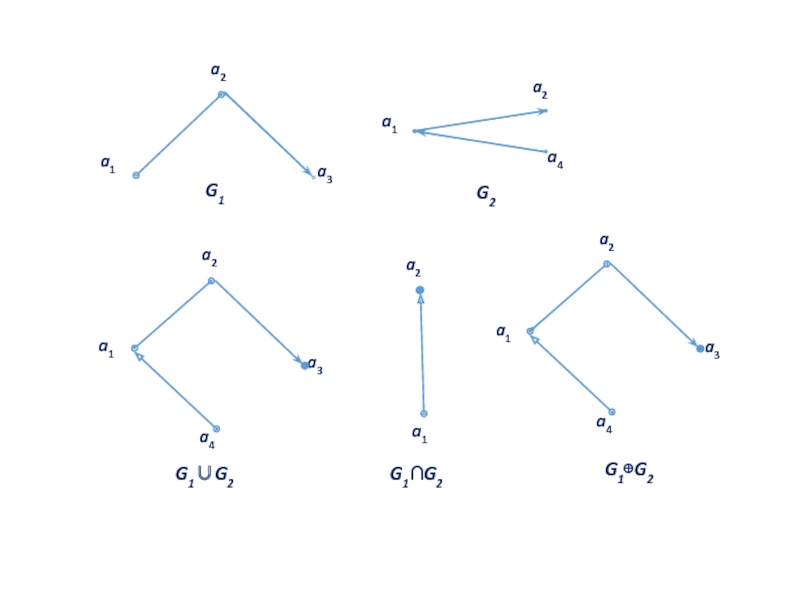
- 26. Операцией добавления к графу G = 〈M,
- 27. Операция отождествления вершин a и b графа
- 29.
- 30. Операцией добавления к графу G = 〈
- 32. Соединением G1 + G2 графов G1 и
- 34. × =
- 35. Говорят, что два графа G1(V1,E1)
- 36. рефлексивность: G ~ G, где требуемая биекция
- 38. Теорема Графы изоморфны тогда и только
- 39. Граф G'(V’, E') называется подграфом графа G(V,
- 40. Количество ребер, инцидентных вершине v, называется степенью
- 41. Если степень вершины равна 0 (то есть
- 42. Маршрутом в графе называется чередующаяся последовательность вершин
- 43. Если все ребра различны, то маршрут называется
- 44. 1.1, 3,
- 45. Важным понятием теории графов является связность. Граф
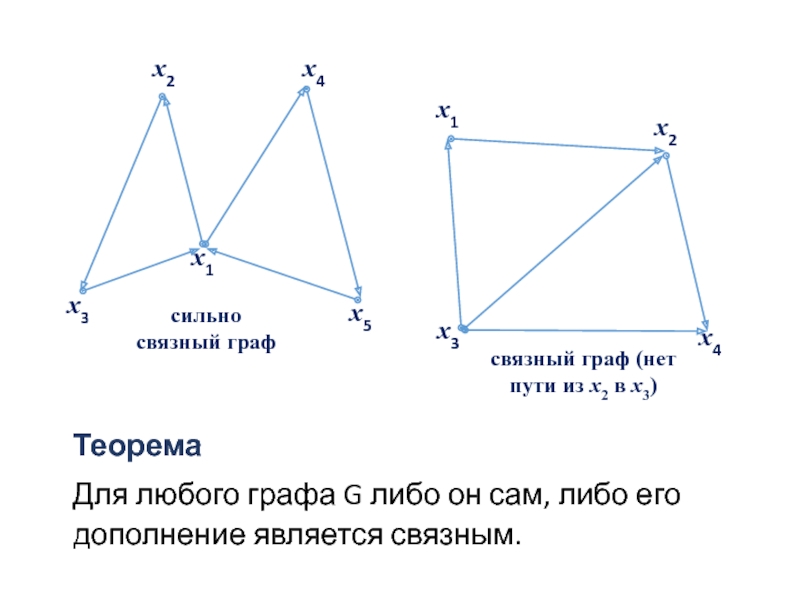
- 46. Теорема Для любого графа G либо он сам, либо его дополнение является связным.
- 47.
- 48.
- 49. Метрические характеристики графа
- 50.
- 51. Пример. Здесь е(х1)= е(х2)= е(х4)= е(х6)=3, е(х3)=
- 52. Обходы графов
- 53. На языке теории графов задача формулируется следующим
- 54. Цикл, содержащий все ребра мультиграфа, называется эйлеровым,
- 55. Выбрать произвольно некоторую вершину а. Выбрать произвольно
- 57. Будем говорить, что набор реберно непересекающихся цепей
- 58. Граф называется гамильтоновым, если в нем имеется
- 59. Несмотря на схожесть задач о нахождении эйлеровых
- 60. Теорема Если для любых двух
- 61. С задачей нахождения гамильтонова цикла связана задача
- 62. Пусть граф задает сеть коммуникаций между фиксированными
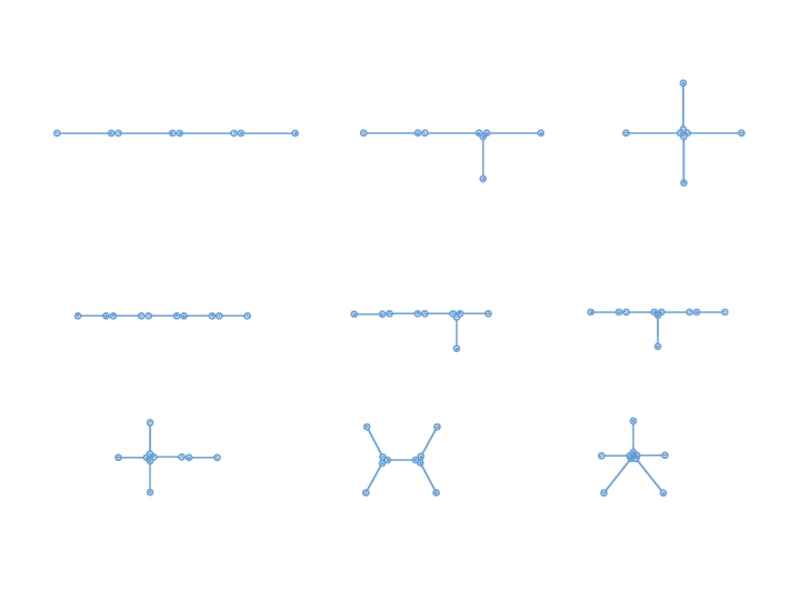
- 63. Деревья заслуживают отдельного и подробного рассмотрения по
- 64. Деревья являются самым распространенным классом графов, применяемых в программировании, причем в самых разных ситуациях.
- 65. Граф без циклов называется ациклическим, или лесом.
- 66. В связном графе G выполняется неравенство
- 69. Пусть G - (М, R) — неорграф.
- 70. Понятие остова для орграфа G определяется как
- 71. Теорема. Для неoрграфа G без петель
- 72. Пример В качестве остова графа G, изображенного
- 73. Из теоремы вытекает Следствие Число ребер
- 74. Число v(G) = m - n +
- 75. Очевидны следующие два следствия: Следствие
- 76. При решении прикладных задач часто возникает необходимость
- 77. Разместим вершины из М по этажам таким
- 79. Опишем обход графа по глубине. При таком,
- 81. При обходе графа по ширине просмотр вершин
- 82. Очевидно, что при обходе всех вершин оба
- 83. Если дерево является достаточно широким, а висячие
- 84. При компьютерной реализации обходов по глубине и
- 85. Определим по индукции понятие упорядоченного дерева: пустое
- 86. Если T1, T2, …, Tn – упорядоченные
- 87. Пример Упорядоченному дереву (1, (2, (4),
- 88. Упорядоченное дерево может также интерпретироваться в виде
- 89. Тезис Любая иерархическая классификационная схема интерпретируется некоторым
- 90. Частным случаем упорядоченного дерева является бинарное дерево.
- 91. а б
- 92. Планарность графов
- 93. Ранее уже отмечалось, что возможно несколько изображений
- 94. Таким образом, возникает задача построения и исследования
- 95. Все планарные графы укладываются на плоскости (имеют плоскую укладку).
- 96. Очевидно, что Всякий подграф планарного графа планарен.
- 97. Гранью планарного графа называется множество точек плоскости,
- 98. Пусть n,m,f — соответственно число вершин, ребер
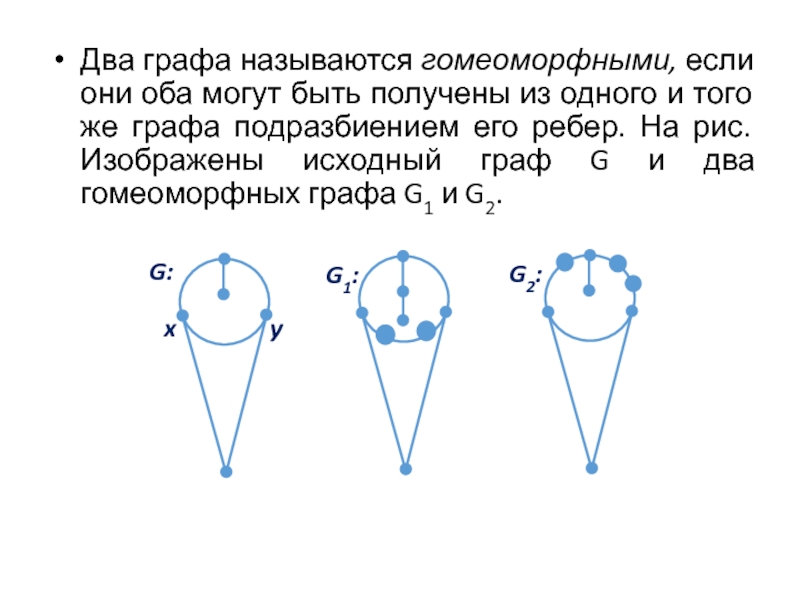
- 99. Два графа называются гомеоморфными, если они оба
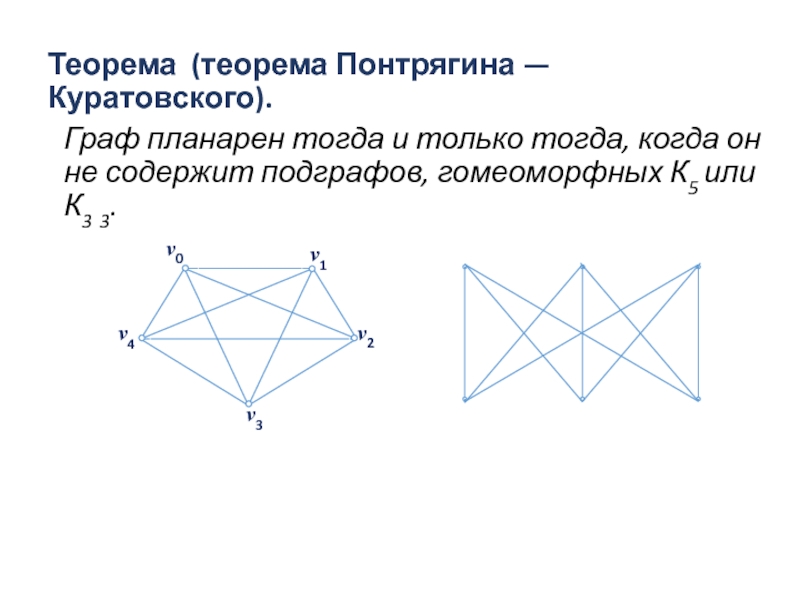
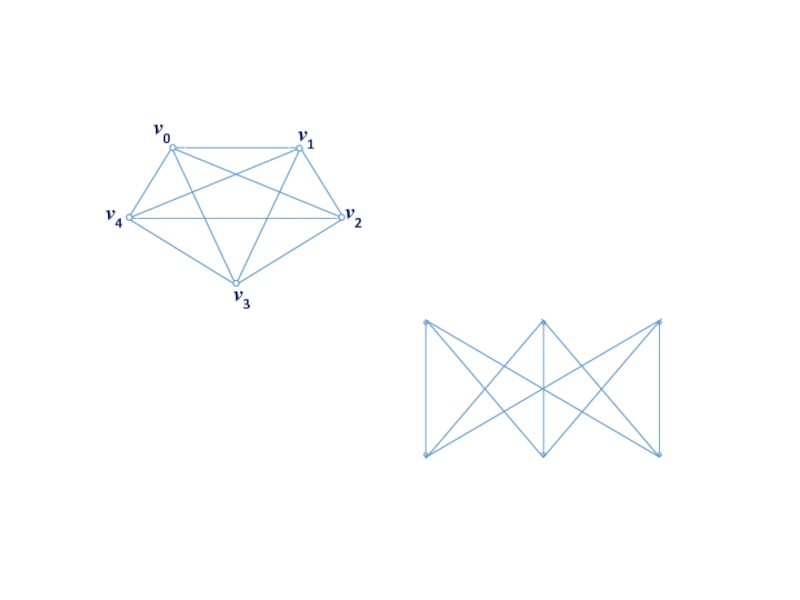
- 100. Теорема (теорема Понтрягина —Куратовского). Граф планарен тогда
- 101. Эквивалентная форма критерия планарности описана в следующей
- 103. Для непланарных графов вводятся характеристики, представляющие ту
- 104. Важнейшая характеристика непланарного графа— его толщина t(G)
- 105. для толщины связного (n,т) графа справедливы такие
- 106. Задачи раскраски вершин и ребер графа занимают
- 107. Пусть G = (S,U) — неориентированный граф.
- 108. В теории хроматических графов существует так называемая
- 109. Легко найти хроматические числа некоторых известных графов, например,—
- 110. Обозначим через P(G) наибольшую из степеней вершин
- 111. Теорема Для любого связного (n,т)- графа
- 112. Теорема Для любого n -вершинного графа G верно неравенство
- 113. Проблема раскраски планарных графов является одной из
- 114. Попытки обосновать эту гипотезу привели к ряду
- 115. Трудность проблемы четырех красок привела к появлению
- 116. В 1976 г. научному коллективу под руководством
- 117. В заключение рассмотрим очень простой алгоритм последовательной
- 118. Алгоритм последовательной раскраски содержит два правила: Произвольной
- 119. Теорема (теорема Кенига) Граф двуцветен тогда и
- 120. ?
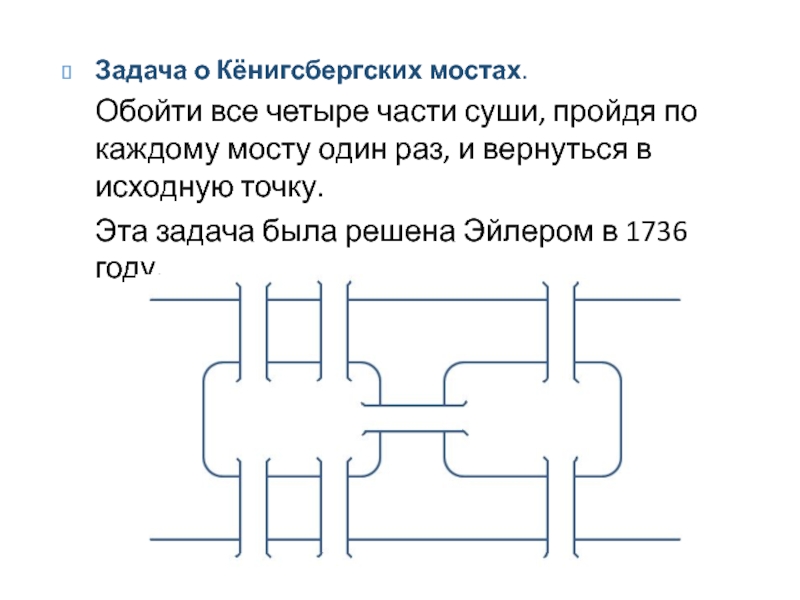
Слайд 2Задача о Кёнигсбергских мостах.
Обойти все четыре части суши, пройдя по
Эта задача была решена Эйлером в 1736 году.
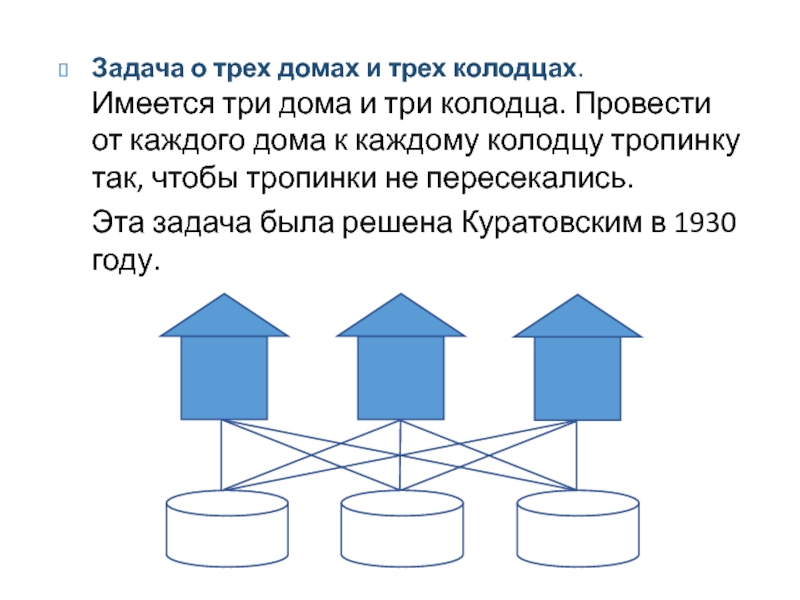
Слайд 3Задача о трех домах и трех колодцах. Имеется три дома и
Эта задача была решена Куратовским в 1930 году.
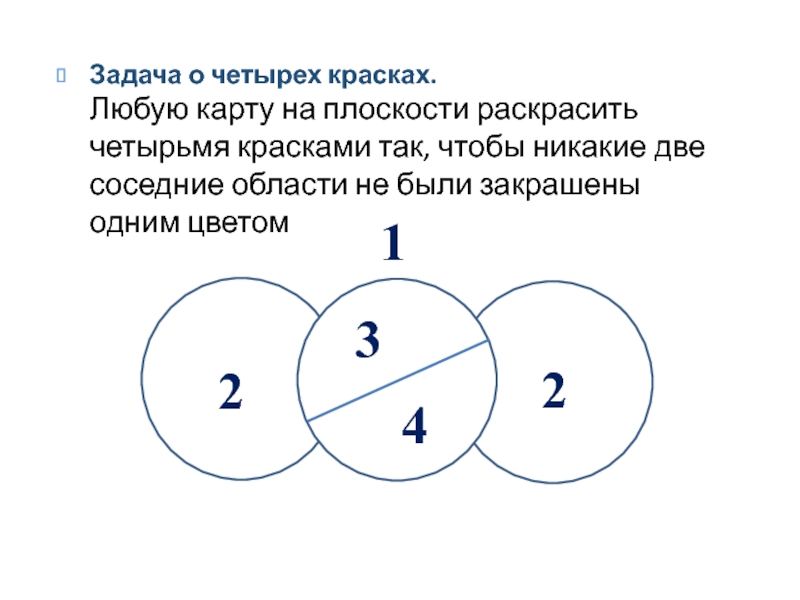
Слайд 4Задача о четырех красках. Любую карту на плоскости раскрасить четырьмя красками так,
Слайд 5
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Графом G (V , Е) называется совокупность двух множеств —
непустого множества V (множества вершин) и
множества Е – бинарного отношения, определённого на множестве V .
Число вершин графа G обозначим n, а число ребер - m:
Слайд 6
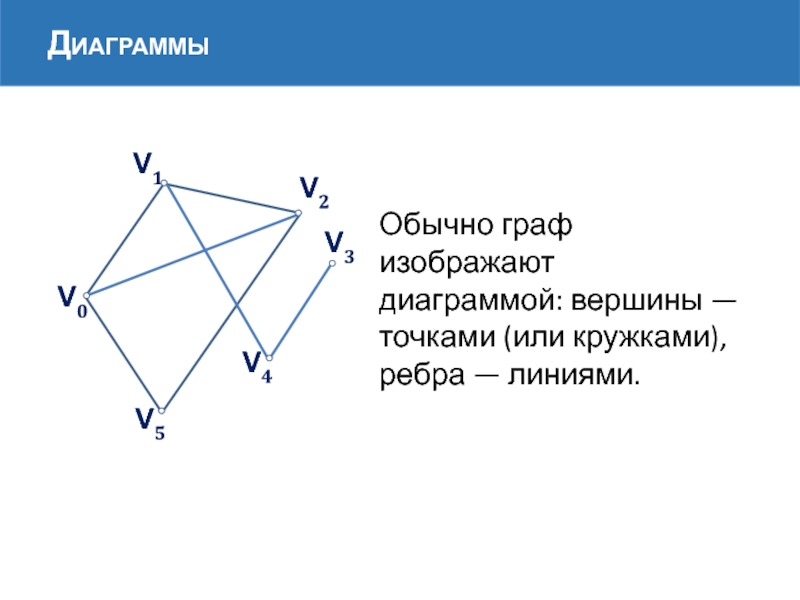
Обычно граф изображают диаграммой: вершины — точками (или кружками),
ребра —
Диаграммы
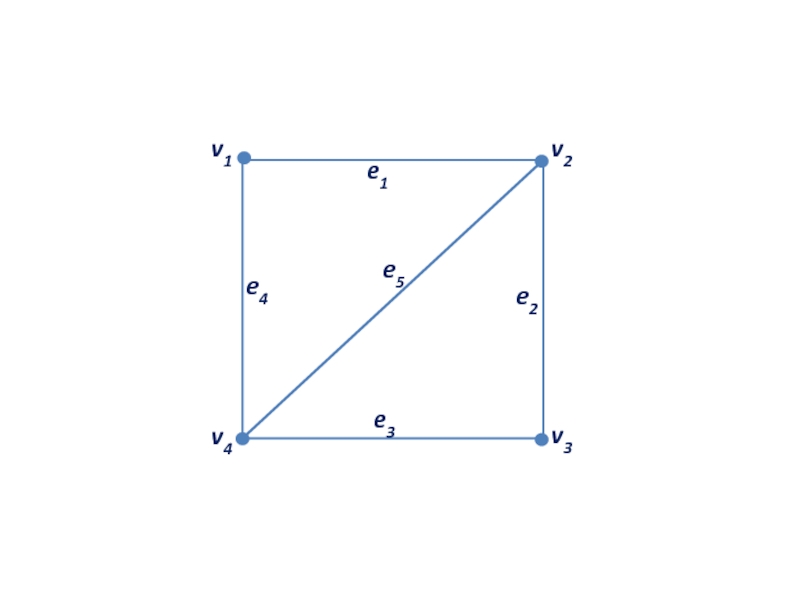
Слайд 7 Пусть v1, v2 — вершины, e = (v2, v1)
вершина v1 и ребро е инцидентны, вершина v2 и ребро е также инцидентны.
Два ребра, инцидентные одной вершине, называются смежными;
две вершины, инцидентные одному ребру, также называются смежными.
Смежность
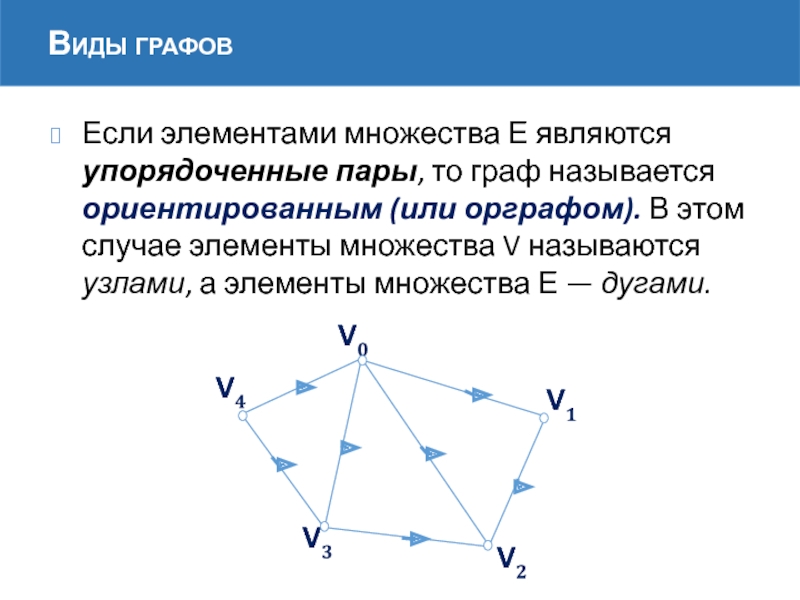
Слайд 9Если элементами множества Е являются упорядоченные пары, то граф называется ориентированным
Виды графов
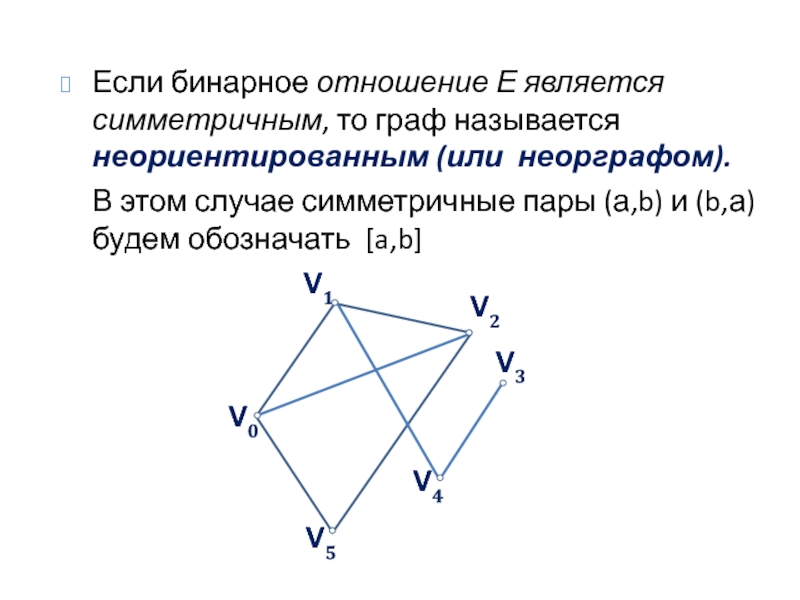
Слайд 10Если бинарное отношение Е является симметричным, то граф называется неориентированным (или
В этом случае симметричные пары (а,b) и (b,а) будем обозначать [a,b]
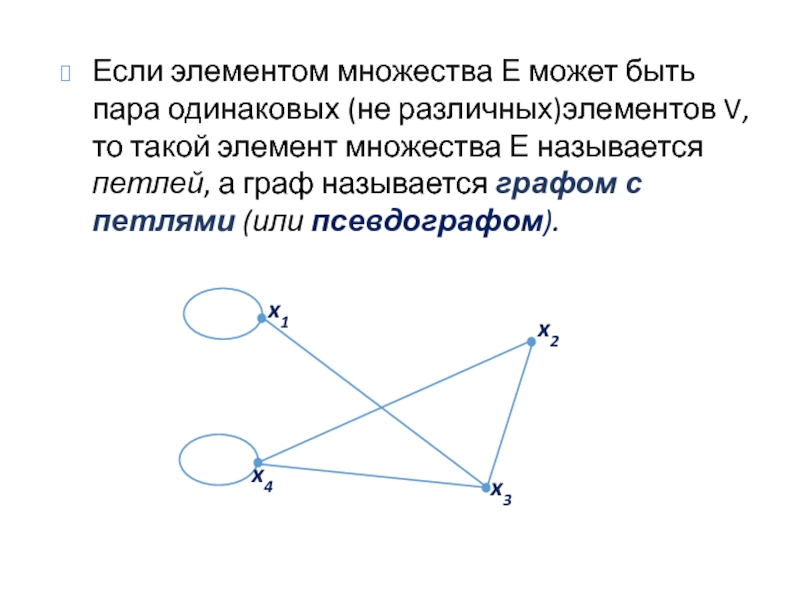
Слайд 11Если элементом множества Е может быть пара одинаковых (не различных)элементов V,
Слайд 13Если Е является не множеством, а набором, содержащим несколько одинаковых элементов,
Слайд 14Если элементами множества Е являются не обязательно двухэлементные, а любые подмножества множества
Слайд 15Если задана функция F: V→М и/или F: Е→М, то множество М
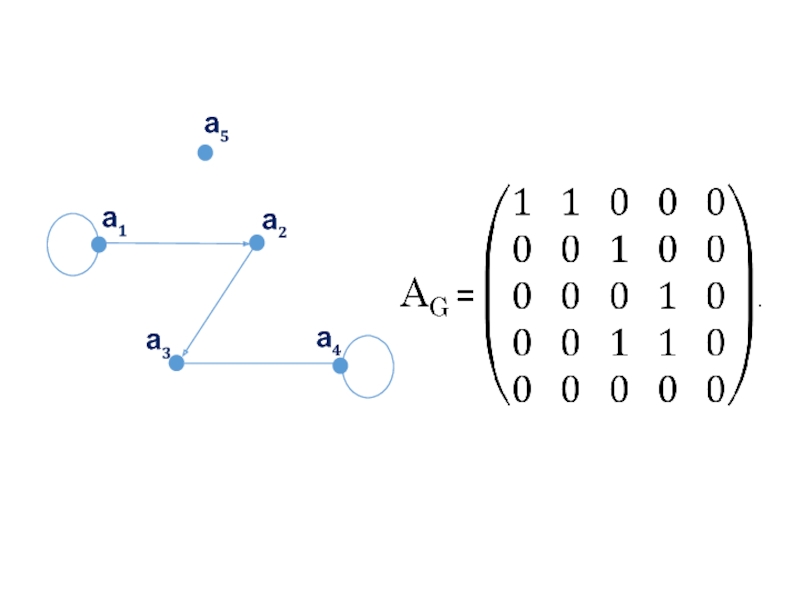
Слайд 17Пусть G= (М, R) - граф, в котором множество вершин имеет
М = (a1, a2, ... ,an}.
Матрицей смежности
A= (Aij) графа G называется матрица порядка n, определенная следующим образом:
если G — неорграф, то матрица смежности а симметрична, т. е. не меняется при тран-спонировании: aT = a.
Слайд 19Если Aij = 1, то вершина aj называется последователем вершины ai,
Если G — мулътиграф, то в матрице смежности a элемент Aij по определению равен числу дуг, исходящих из вершины ai и заходящих в вершину aj .
Слайд 20
Матрица инцидентности
Если число вершин графа G равно n, а число ребер
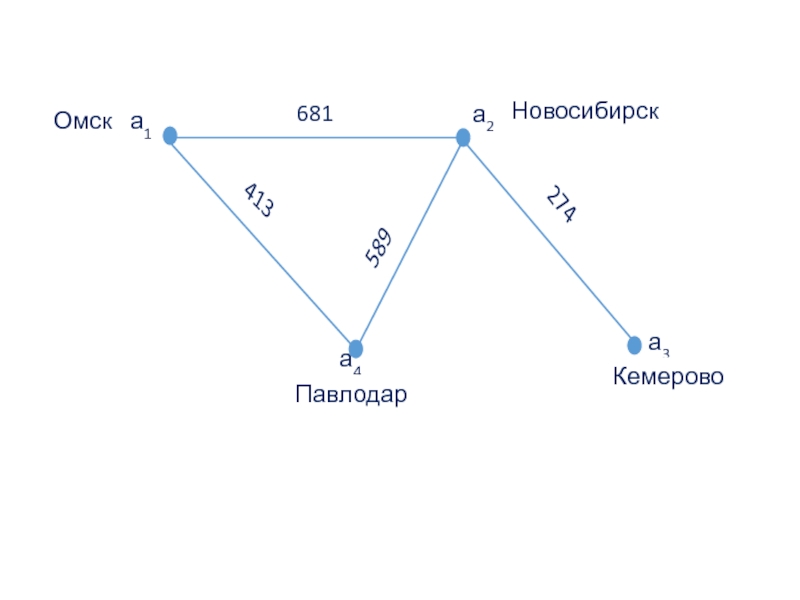
Слайд 23 Информацию о весах дуг во взвешенном графе можно представлять в виде
W =
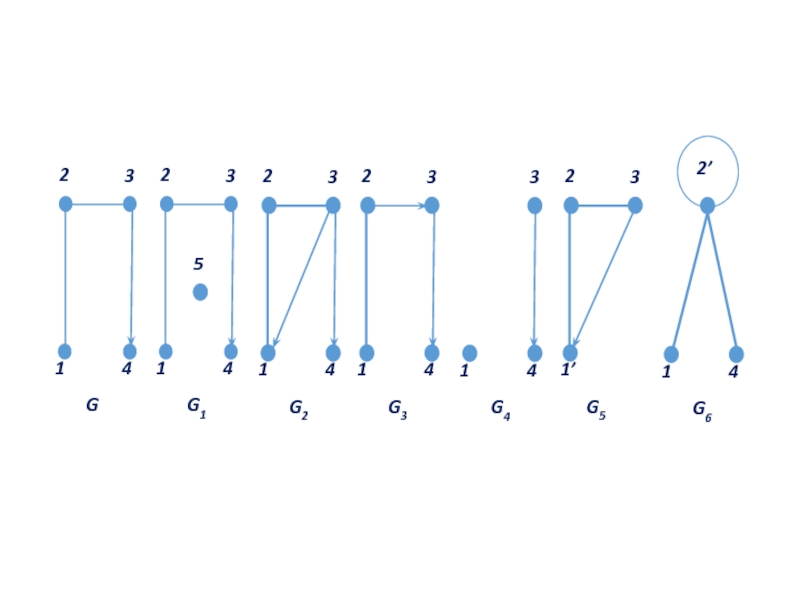
Слайд 25Граф G'(V’, E') называется подграфом графа G(V, E) (обозначается G’⊂ G),
Если V’⊂ V &Е' ⊂ E&(V’≠ V ∨ Е' ≠ Е), то граф G' называется собственным подграфом графа G.
Подграф G'(V',E'} называется правильным подграфом графа G(V,E), если G' содержит все возможные ребра G:
u,v∊V’ (u,v) ∊ E⇒(u,v) ∊E'.
Правильный подграф G'(V’, E') графа G(V, E) определяется подмножеством вершин V’.
Элементы графов
Слайд 26 Операцией добавления к графу G = 〈M, R〉 вершины а образуется
Под операцией удаления дуги (a, b) из графа G понимается операция, заключающаяся в удалении пары (a, b) из множества дуг R, в результате получается граф 〈M, R \ {( a, b)}〉. Операция удаления вершины а из графа G заключается в удалении вершины a вместе с инцидентными ей дугами:
〈M\ {a}, R \ {(b, c)| b = a или с = а}〉
Слайд 27 Операция отождествления вершин a и b графа G = 〈M, R〉
〈(М \ {a, b}) ∪ { а’}, (R\ {(c, d)|c = a или d = a, или с = b, или d = b}) ∪ {(а’, c)| (а, c) ∈ R, или (b, c) ∈ R} ∪ {(c, а’)| (c, a) ∈ R, или (с, b) ∈ R }〉.
Говорят, что построенный граф получается из графа G отождествлением вершин a и b. В случае, когда a и b соединены дугой, операцию отождествления вершин a и b называют стягиванием дуги (a, b).
Слайд 30 Операцией добавления к графу G = 〈 M ∪ {a}, R〉
〈 M \ {a}, R \ {(b,c)|b=a или c=a}〉.
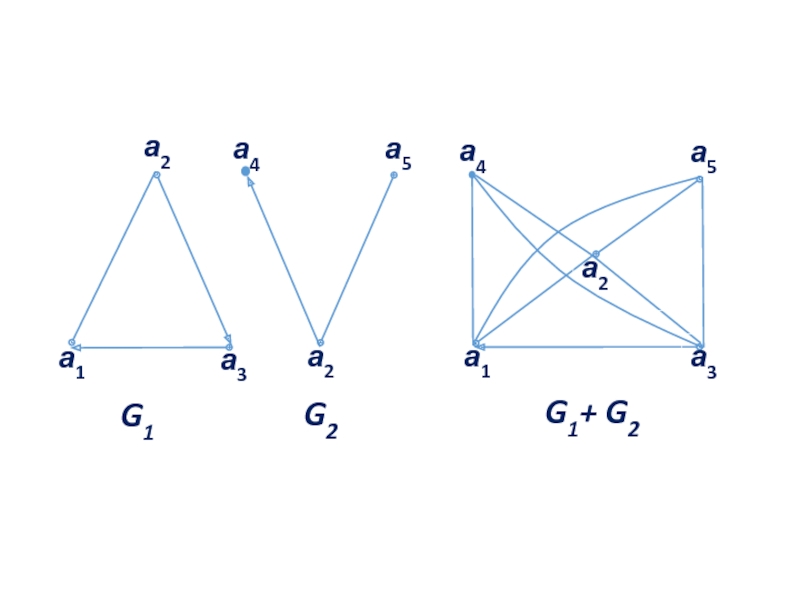
Слайд 32 Соединением G1 + G2 графов G1 и G2 называется граф 〈M1∪M2,
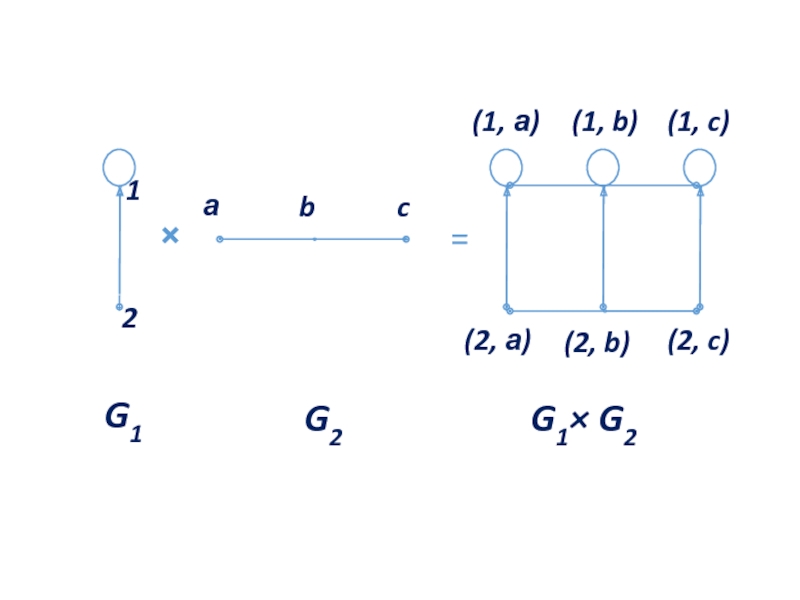
Произведением G1 × G2 графов G1 и G2 называется граф 〈M1 × M2, R〉, в котором ((a1, b1), (a2, b2)) ∈ R тогда и только тогда, когда a1 = a2 и (b1, b2) ∈ R2, или b1=b2 и (a1,a2) ∈ R1.
Слайд 35Говорят, что два графа G1(V1,E1) и G2(V2,E2)
e1 = (u,v) ∊ Е1<=> e2 = (h(u),h(v)) ∊ E2,
Изоморфизм графов есть отношение эквивалентности. Действительно, изоморфизм обладает всеми необходимыми свойствами:
Изоморфизм графов
Слайд 36рефлексивность: G ~ G, где требуемая биекция суть тождественная функция;
симметричность: если
транзитивность: если g1 ~ G2 с биекцией h и G2 ~ G3 с биекцией g, то g1 ~ G3 с биекцией g∙h.
Графы рассматриваются с точностью до изоморфизма, то есть рассматриваются классы эквивалентности по отношению изоморфизма.
Слайд 38Теорема
Графы изоморфны тогда и только тогда, когда их матрицы смежности
Теорема
Графы (орграфы) изоморфны тогда и только тогда, когда их матрицы инцеденций получаются друг из друга произвольными перестановками строк и столбцов.
Слайд 39Граф G'(V’, E') называется подграфом графа G(V, E) (обозначается G’⊂ G),
Если V’⊂ V &Е' ⊂ E&(V’≠ V ∨ Е' ≠ Е), то граф G' называется собственным подграфом графа G.
Подграф G'(V',E'} называется правильным подграфом графа G(V,E), если G' содержит все возможные ребра G:
u,v∊V’ (u,v) ∊ E⇒(u,v) ∊E'.
Правильный подграф G'(V’, E') графа G(V, E) определяется подмножеством вершин V’.
Элементы графов
Слайд 40Количество ребер, инцидентных вершине v, называется степенью (или валентностью) вершины v
Обозначим минимальную степень вершины графа G через δ(G), а максимальную — через ∆(G)
Если степени всех вершин равны k, то граф называется регулярным степени k
Степень регулярности является инвариантом графа и обозначается r(G). Для нерегулярных графов r(G) не определено.
Валентность
Слайд 41 Если степень вершины равна 0 (то есть d(v) = 0), то
Для орграфа число дуг, исходящих из вершины v, называется полустепенью исхода, а входящих — полустепенью захода. Обозначаются эти числа, соответственно, d-(v) и d+(v).
ТЕОРЕМА (Эйлера)
Сумма степеней вершин графа равна удвоенному количеству ребер: = 2m.
Слайд 42Маршрутом в графе называется чередующаяся последовательность вершин и ребер v0,e1,v1,e2,v2,...,ek,vk, в
Это определение подходит также для псевдо-, мульти- и орграфов. Для «обычного» графа достаточно указать только последовательность вершин или только последовательность ребер.
Если v0= vk, то маршрут замкнут, иначе открыт.
Маршруты, цепи, циклы
Слайд 43Если все ребра различны, то маршрут называется цепью. Если все вершины
Цепь, соединяющая вершины u и v, обозначается (u, v). Очевидно, что если есть цепь, соединяющая вершины u и v, то есть и простая цепь, соединяющая эти вершины.
Замкнутая цепь называется циклом; замкнутая простая цепь называется простым циклом. Число циклов в графе G обозначается z(G). Граф без циклов называется ациклическим.
Для орграфов цепь называется путем, а цикл — контуром.
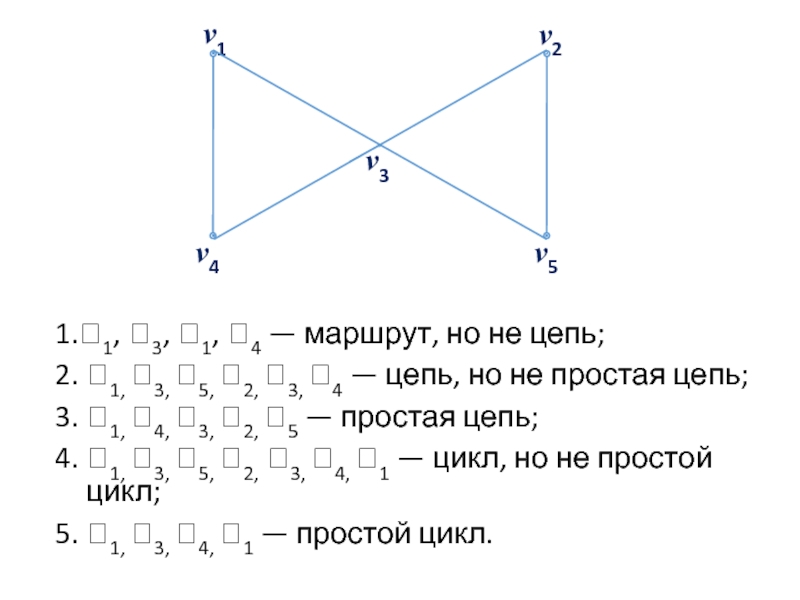
Слайд 44
1.1, 3, 1, 4 — маршрут, но не цепь;
2. 1, 3,
3. 1, 4, 3, 2, 5 — простая цепь;
4. 1, 3, 5, 2, 3, 4, 1 — цикл, но не простой цикл;
5. 1, 3, 4, 1 — простой цикл.
Слайд 45 Важным понятием теории графов является связность. Граф называется связным, если любые
Для орграфа существует ещё понятие сильной связности. Для этого определим понятие пути.
Путь – это ориентированный маршрут. Поэтому если для установления простой (или слабой) связности графа ориентацию его дуг принимать в расчёт не следует, то для установления сильной связности это необходимо. Орграф называется сильно связным, если для любых двух вершин xI, xj ∈ s найдётся путь с началом в xi и концом в xj. Для неориентированного графа понятие пути и маршрута совпадают.
Связность
Слайд 51 Пример. Здесь е(х1)= е(х2)= е(х4)= е(х6)=3, е(х3)= е(х7)=4, е(х5)=2. Таким образом,
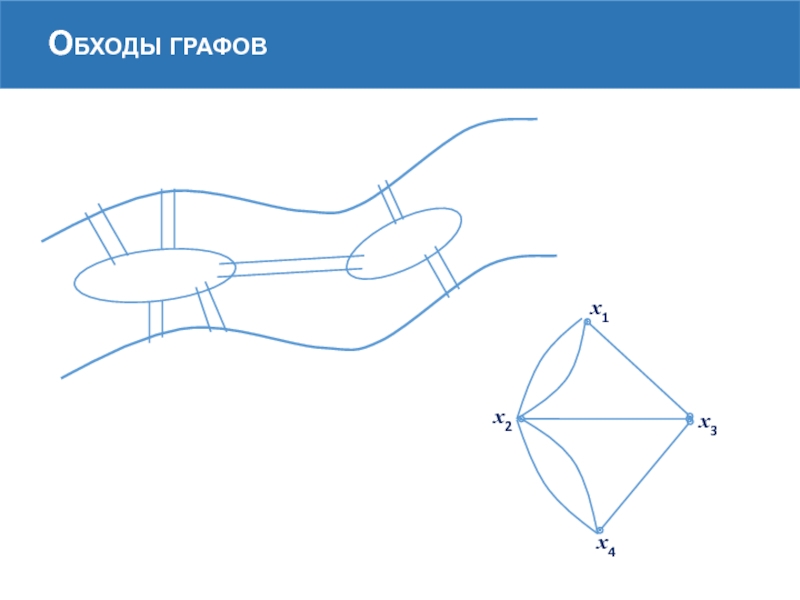
Слайд 53 На языке теории графов задача формулируется следующим образом: существует ли в
Выдающимся математиком и механиком Л. Эйлером сформулирован и доказан критерий того, что связный неориентированный мультиграф имеет цикл, содержащий все ребра данного мультиграфа.
Слайд 54Цикл, содержащий все ребра мультиграфа, называется эйлеровым, и мультиграф, в котором
Теорема
Связный неориентированный мультиграф тогда и только тогда является эйлеровым, когда степень каждой из его вершин — четное число.
Слайд 55Выбрать произвольно некоторую вершину а.
Выбрать произвольно некоторое ребро и, инцидентное а,
Каждому пройденному ребру присвоить номер, на единицу больший номера предыдущего.
Находясь в вершине х, не выбирать ребро, соединяющее х с а, если имеется возможность иного выбора.
Находясь в вершине х, не выбирать ребро, при удалении которого граф, образованный непронумерованными ребрами, распадается на две компоненты связности, каждая из которых имеет хотя бы по одному ребру.
После того как в графе будут занумерованы все ребра, образуется эйлеров цикл, причем порядок нумерации соответствует последовательности обхода ребер.
алгоритм построения эйлерова цикла
Слайд 57 Будем говорить, что набор реберно непересекающихся цепей покрывает граф G, если
Теорема
Если связный граф содержит k вершин нечетной степени, то минимальное число покрывающих его реберно непересекающихся цепей равно k/2.
В частности, при k = 2 граф имеет цепь, которая соединяет вершины нечетной степени и содержит все ребра графа. Цепь, содержащая все ребра графа, называется эйлеровой.
Слайд 58Граф называется гамильтоновым, если в нем имеется простой цикл, содержащий каждую
Гамильтоновой называется и простая цепь, содержащая все вершины графа.
Очевидно, что любой граф, ребра которого образуют простой цикл, является гамильтоновым.
обходы вершин графа
Слайд 59Несмотря на схожесть задач о нахождении эйлеровых и гамильтоновых циклов, решение
Известны следующие достаточные условия существования гамильтоновых циклов в связном неорграфе G без петель, имеющем больше 3 вершин:
Слайд 60
Теорема
Если для любых двух различных несмежных вершин а, и b
deg a + deg b ^ n,
то существует гамильтонов цикл.
Следствие
Если для любой вершины а графа G выполнено условие
deg a ^ n/2,
то существует гамильтонов цикл.
Слайд 61 С задачей нахождения гамильтонова цикла связана задача коммивояжера.
Район, который должен
Математическая постановка задачи выглядит так: требуется найти гамильтонов цикл минимального веса.
Слайд 62Пусть граф задает сеть коммуникаций между фиксированными центрами. Необходимо построить маршрут,
Имеется станок с числовым программным управлением, который высверливает отверстия в печатных платах по заданной программе.
Составляя граф, в котором вершины соответствуют требуемым отверстиям, получаем задачу нахождения обхода вершин, такого, что суммарное время, затраченное на него, было бы минимальным.
Некоторые практические задачи, сводящиеся к задаче коммивояжера
Слайд 63 Деревья заслуживают отдельного и подробного рассмотрения по двум причинам.
Деревья являются в
Деревья
Слайд 64Деревья являются самым распространенным классом графов, применяемых в программировании, причем в
Слайд 65Граф без циклов называется ациклическим, или лесом. Связный ациклический граф называется
Прилагательное «свободное» употребляется в том случае, когда нужно подчеркнуть отличие деревьев от других объектов, родственных деревьям: ориентированных деревьев, упорядоченных деревьев и т. д.
Основные определения
Слайд 66В связном графе G выполняется неравенство
q(G) ≥ p(G) — 1.
Граф G, в котором q(G)=p(G)-1, называется древовидным.
В ациклическом графе G z(G) = 0.
Пусть u, v — несмежные вершины графа G,
х = (u, v) ∉ Е.
Если граф G + х имеет только один простой цикл,
z(G + х) = 1, то граф G называется субциклическим.
Слайд 69 Пусть G - (М, R) — неорграф.
Часть G' = (М',
Таким образом, если G — связный граф, то остов G' является деревом, которое будем называть остовным деревом графа G.
Остов графа
Слайд 70 Понятие остова для орграфа G определяется как часть G' графа G,
Аналогично вводится понятие остовного дерева для связного орграфа G.
Очевидно, что в каждом графе существует остов: разрушая в каждой связной компоненте циклы, т. е. удаляя лишние ребра, получаем остов.
Слайд 71Теорема.
Для неoрграфа G без петель содержащего n вершин следующие условия
G — дерево;
G — связный граф, содержащий n - 1 ребро;
G — ациклический граф, содержащий n - 1 ребро;
любые две несовпадающие вершины графа G соединяет единственная простая цепь;
G — ациклический граф, такой, что если какую-либо пару егo несмежных вершин соединить ребром, то полученный граф будет содержать ровно один цикл.
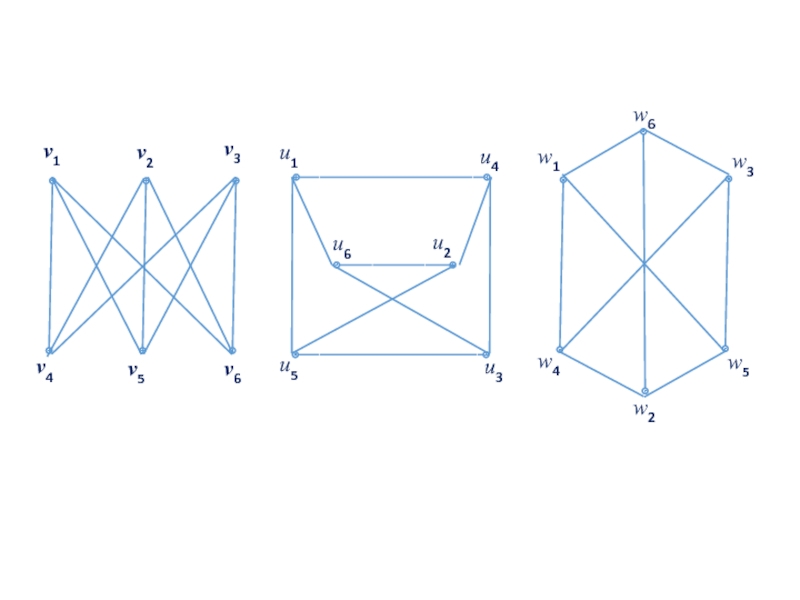
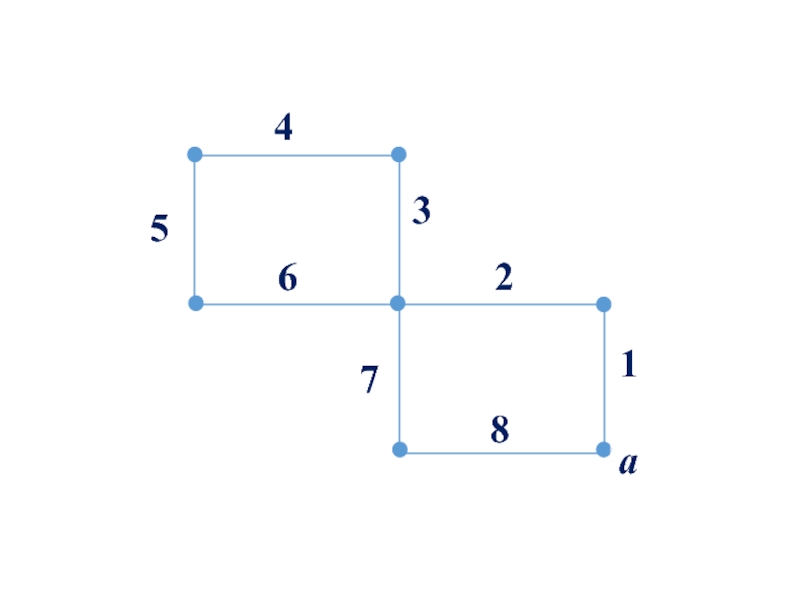
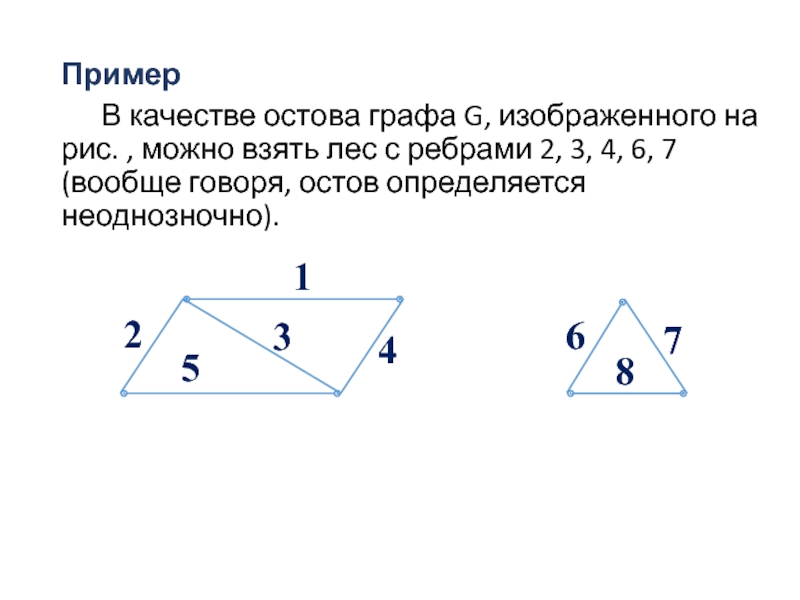
Слайд 72Пример
В качестве остова графа G, изображенного на рис. , можно взять
Слайд 73Из теоремы вытекает
Следствие
Число ребер произвольного неорграфа G, которые необходимо удалить
Слайд 74Число v(G) = m - n + с называется цикломатическим числом
Слайд 75Очевидны следующие два следствия:
Следствие
Неорграф G является лесом тогда и только
Следствие
Неорграф G имеет единственный цикл тогда и только тогда, когда v(G) = 1.
Слайд 76 При решении прикладных задач часто возникает необходимость обхода вершин графа, связанная
Пусть G = (М, R) — связный неориентированный граф,
Т — некоторый остов графа G,
a — некоторая фиксированная вершина, называемая корнем дерева Т.
Обходы графа по глубине и ширине
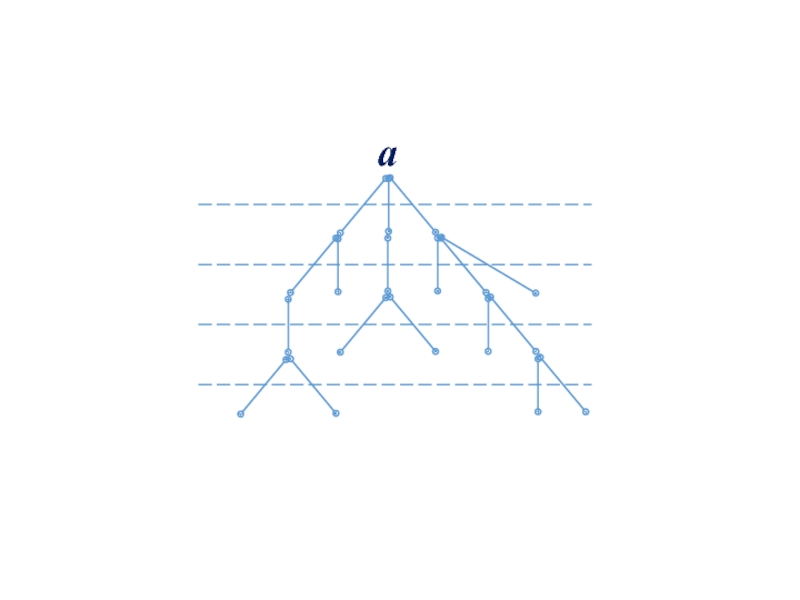
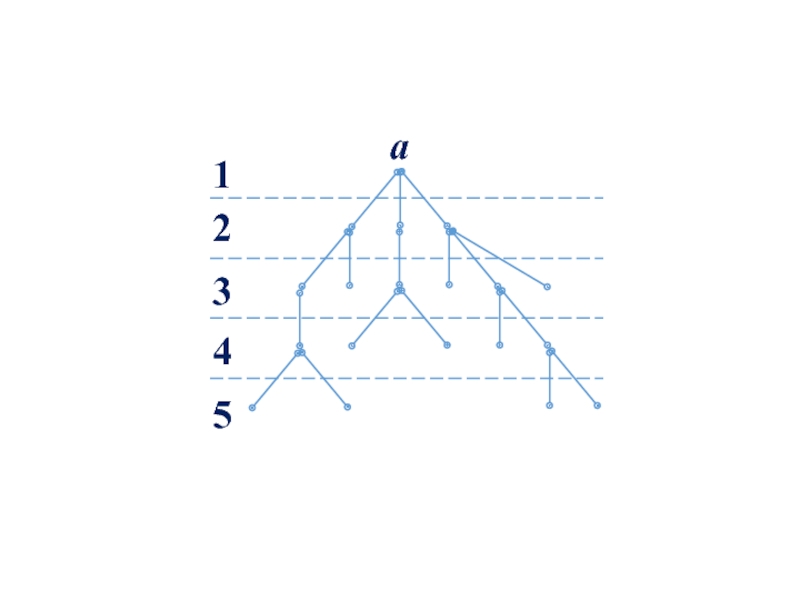
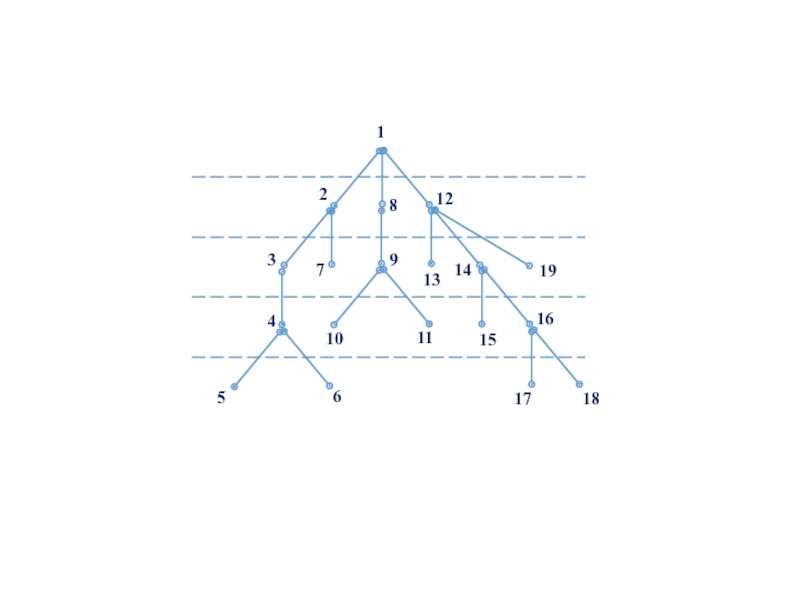
Слайд 77 Разместим вершины из М по этажам таким образом, чтобы корень а
Таким образом, получаем е(а) + 1 этажей, где е(а) — эксцентриситет вершины а.
Слайд 79Опишем обход графа по глубине.
При таком, обходе после очередной рассмотренной вершины
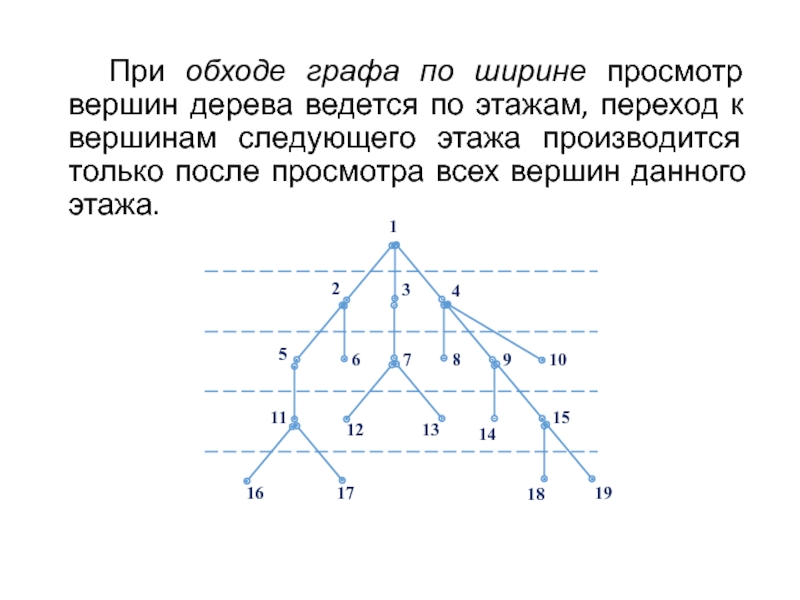
Слайд 81 При обходе графа по ширине просмотр вершин дерева ведется по этажам,
Слайд 82 Очевидно, что при обходе всех вершин оба подхода: поиск в глубину
Если же достаточно найти одну вершину с определенным свойством, то целесообразность применения поиска решения по глубине или по ширине определяется структурой дерева.
Слайд 83 Если дерево является достаточно широким, а висячие вершины расположены на сравнительно
Для глубоких узких деревьев, когда висячие вершины могут встретиться на различных этажах и их разброс по этажам достаточно велик, предпочтение отдается поиску по ширине.
Слайд 84 При компьютерной реализации обходов по глубине и ширине целесообразно использовать задание
Слайд 85Определим по индукции понятие упорядоченного дерева:
пустое множество и список (а), где
если T1, T2, …, Tn – непустые упорядоченные деревья, a – некоторый новый элемент, то список T = (a, T1, T2, …, Tn) образует упорядоченное дерево. При этом элемент a называется корнем упорядоченного дерева Т;
любое упорядоченное дерево строится в соответствии с п. 1 и 2.
Упорядоченные и бинарные деревья
Слайд 86 Если T1, T2, …, Tn – упорядоченные деревья, то список (T1,
Для заданного упорядоченного дерева Т определим множество S(T) его упорядоченных поддеревьев:
если Т = ∅, то S(T) = ∅;
если Т = (a), то S(T) = {(a)};
если Т = (a, T1, T2, …, Tn), то S(T) = S(T1)∪ … ∪ S(Tn)∪{T}.
Непустое упорядоченное дерево T может интерпретироваться в виде системы пронумерованных непустых множеств, каждое из которых взаимно однозначно соответствует упорядоченному поддереву из S(T) так, что:
если T’ – поддерево упорядоченного дерева T”. T’, T”∈ S(T), то для соответствующих множеств Х’ и Х” выполняется включение Х’ ⊆ Х”;
если T’ не является поддеревом упорядоченного дерева T”, T’, T”∈ S(T), соответствующие множества не пересекаются.
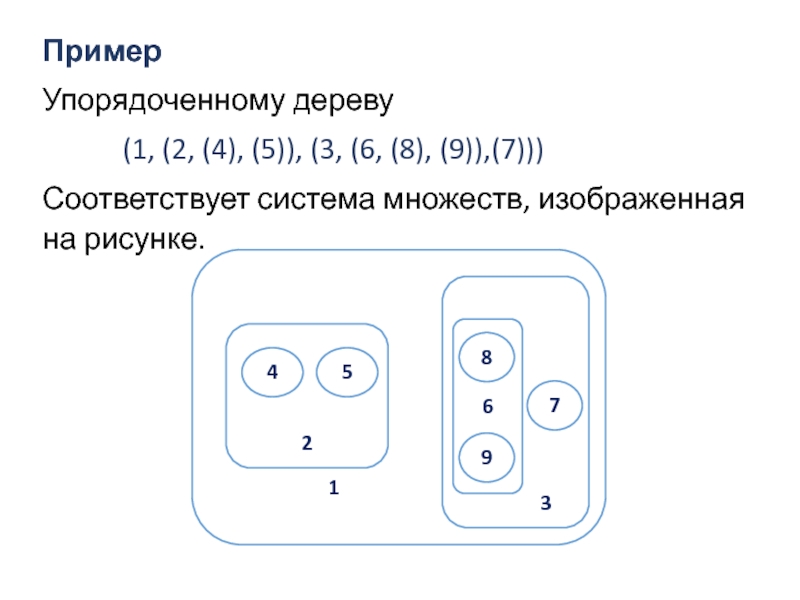
Слайд 87Пример
Упорядоченному дереву
(1, (2, (4), (5)), (3, (6, (8), (9)),(7)))
Соответствует система
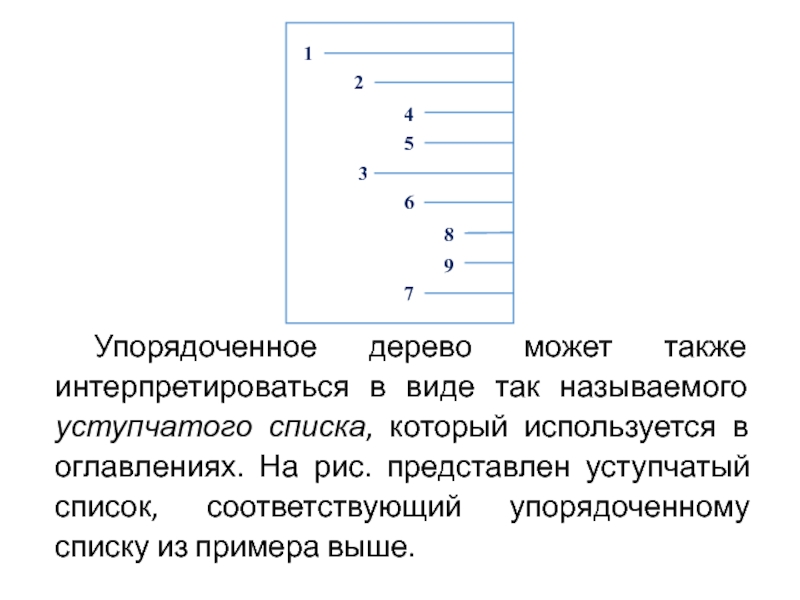
Слайд 88Упорядоченное дерево может также интерпретироваться в виде так называемого уступчатого списка,
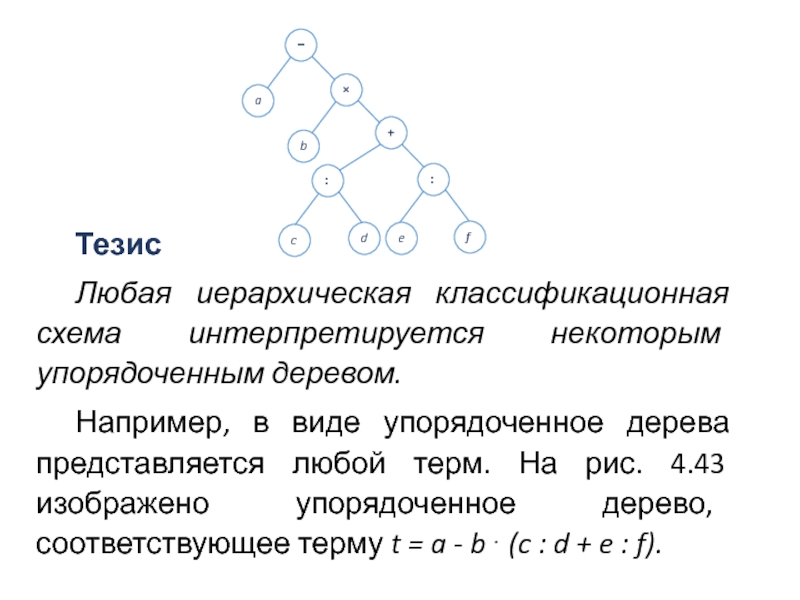
Слайд 89Тезис
Любая иерархическая классификационная схема интерпретируется некоторым упорядоченным деревом.
Например, в виде упорядоченное
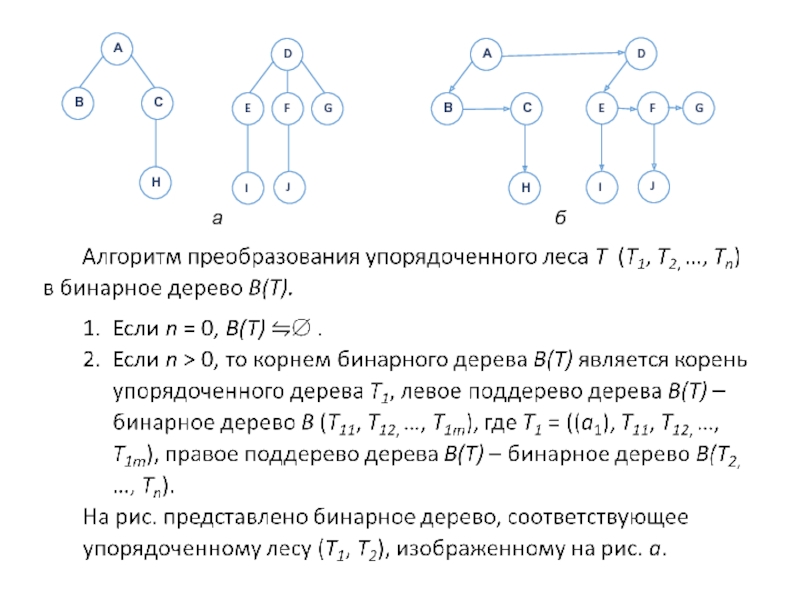
Слайд 90 Частным случаем упорядоченного дерева является бинарное дерево. Определение понятия бинарного дерева
Бинарные деревья имеют более простое устройство, чем упорядоченные, и вместе с тем любой упорядоченный лес взаимно однозначно соответствует некоторому бинарному дереву.
Слайд 93Ранее уже отмечалось, что возможно несколько изображений одного графа, поскольку все
На практике при изготовлении микросхем необходимо выяснить, можно ли схему радиоэлектронного устройства, которая представляет собой граф, изобразить на плоскости без пересечений проводников.
Аналогичная задача возникает при проектировании железнодорожных и других путей, где нежелательны переезды.
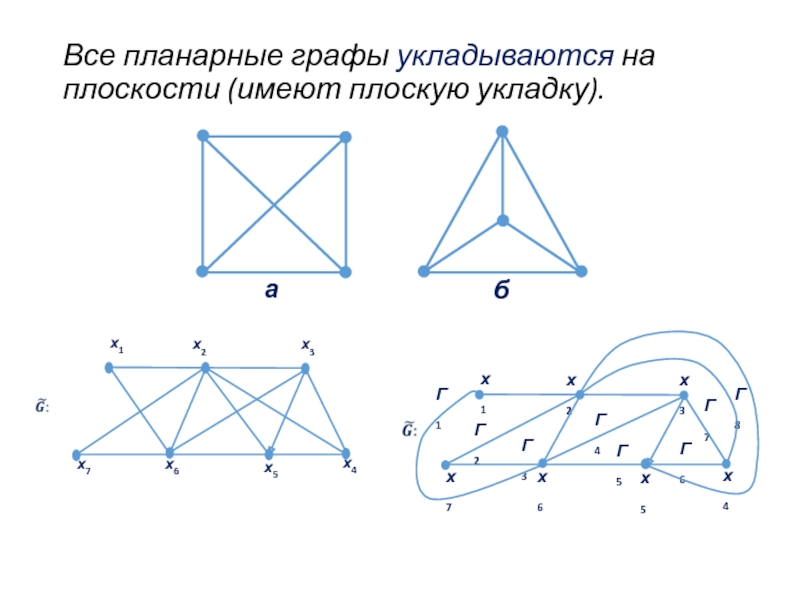
Слайд 94Таким образом, возникает задача построения и исследования плоского графа.
Плоским называется
Любой граф, изоморфный плоскому графу, называется планарным.
Слайд 96Очевидно, что
Всякий подграф планарного графа планарен.
Граф планарен тогда и только тогда,
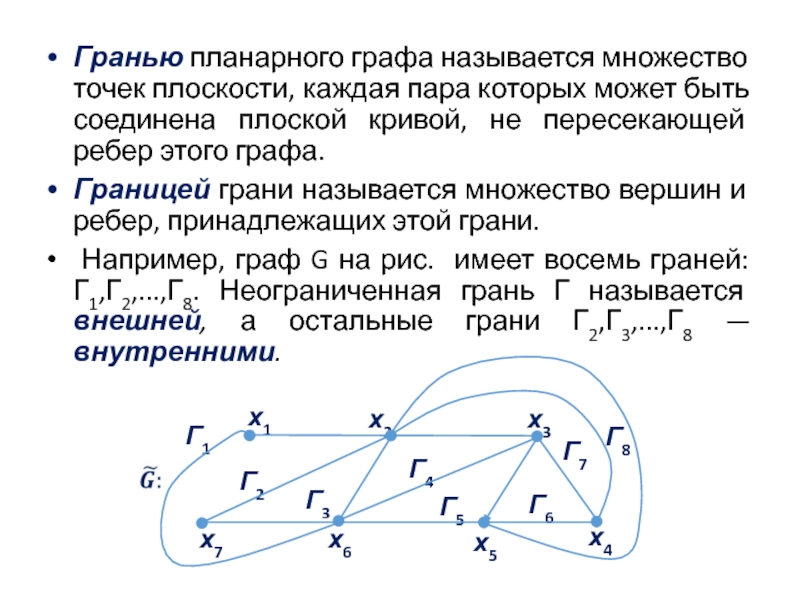
Слайд 97Гранью планарного графа называется множество точек плоскости, каждая пара которых может
Границей грани называется множество вершин и ребер, принадлежащих этой грани.
Например, граф G на рис. имеет восемь граней: Г1,Г2,...,Г8. Неограниченная грань Г называется внешней, а остальные грани Г2,Г3,...,Г8 —внутренними.
Слайд 98 Пусть n,m,f — соответственно число вершин, ребер и граней планарного графа.
Теорема
Для всякого связного планарного графа верно равенство
n-m +f = 2.
Слайд 99Два графа называются гомеоморфными, если они оба могут быть получены из
Слайд 100Теорема (теорема Понтрягина —Куратовского).
Граф планарен тогда и только тогда, когда он
Слайд 101 Эквивалентная форма критерия планарности описана в следующей теореме.
Теорема
Граф планарен тогда и
Слайд 103Для непланарных графов вводятся характеристики, представляющие ту или иную меру непланарности.
Если
Наименьшее число ребер, удаление которых приводит к планарному графу, называется числом планарности или искаженностъю sk(G) графа G.
Для числа планарности полного графа справедлива следующая формула:
Слайд 104Важнейшая характеристика непланарного графа— его толщина t(G) — наименьшее число планарных
Толщина графа равна минимальному числу плоскостей t, при котором граф G разбивается на плоские части Gl,G2,...,Gl.
Очевидно, что толщина планарного графа равна единице.
Слайд 105для толщины связного (n,т) графа справедливы такие оценки
где
Слайд 106Задачи раскраски вершин и ребер графа занимают важное место в истории
Задача раскрашивания графов, имеет также неожиданно широкое применение в программировании, особенно при решении фундаментальных теоретических проблем
Раскраска графов
Слайд 107Пусть G = (S,U) — неориентированный граф.
Раскраской графа называется такое
Таким образом, множество вершин одного цвета является независимым множеством.
Хроматическим числом χ графа G называется минимальное число цветов, требующееся для раскраски G . Если χ = k , то граф называется k -хроматическим.
Слайд 108В теории хроматических графов существует так называемая гипотеза четырех красок, которую
Попытки обосновать эту гипотезу привели к ряду интересных результатов не только по раскраске графов, но и по ряду других разделов теории графов.
Слайд 110 Обозначим через P(G) наибольшую из степеней вершин графа G
Теорема
Для любого
χ(g)
Следующая теорема связывает хроматическое число графа с количеством его вершин и ребер.
Слайд 111Теорема
Для любого связного (n,т)- графа G верны неравенства
где [...] —
Слайд 113Проблема раскраски планарных графов является одной из самых знаменитых проблем теории
В 1879 г. английский математик Кэли четко сформулировал гипотезу четырех красок, которую некоторые авторы с полным основанием называют «болезнью четырех красок».
Слайд 114Попытки обосновать эту гипотезу привели к ряду интересных результатов не только
Гипотеза четырех красок.
Всякий планарный граф 4-раскрашиваем.
Попытки доказать эту гипотезу привели в 1890г. к появлению теоремы Хивуда.
Теорема
Всякий планарный граф 5-раскрашиваем
Слайд 115Трудность проблемы четырех красок привела к появлению большого числа равносильных ей
В конце 60-х гг. прошлого века эта проблема была сведена к исследованию большого, но конечного множества так называемых неустранимых конфигураций, число которых оказалось равно 1482
Слайд 116В 1976 г. научному коллективу под руководством К. Аппеля и В.
Таким образом, хотя такое доказательство очень сложно повторить, можно считать, что формально гипотеза четырех красок доказана.
Слайд 117 В заключение рассмотрим очень простой алгоритм последовательной раскраски графа. Этот алгоритм
Только для некоторых классов графов, например полных k -дольных, последовательная раскраска минимальна.
Слайд 118Алгоритм последовательной раскраски содержит два правила:
Произвольной вершине х графа G присваивается
Если вершины x1,x2,…,xi раскрашены k цветами 1,2,…,k , k














![Соединением G1 + G2 графов G1 и G2 называется граф 〈M1∪M2, R1∪R2∪ {[a, b]|a ∈M1,](/img/tmb/3/292207/82fd6561b489bf523f91464275f03b6f-800x.jpg)


















































![для толщины связного (n,т) графа справедливы такие оценки где [...] — целая часть числа,](/img/tmb/3/292207/1ae1f22804462c2f8caaa984e4d90fd3-800x.jpg)





![Теорема Для любого связного (n,т)- графа G верны неравенствагде [...] — целая часть, а {..}](/img/tmb/3/292207/3a7851bd2c34ded3d0540c9785ff6cd7-800x.jpg)














