- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрия. Төртбұрыштар. Көпбұрыштар. Параллелограмм. Трапеция. Фалес теоремасы презентация
Содержание
- 1. Геометрия. Төртбұрыштар. Көпбұрыштар. Параллелограмм. Трапеция. Фалес теоремасы
- 2. Мазмұны Төртбұрыштар Көпбұрыштар Параллелограмм
- 3. А В С D
- 4. Көпбұрыш ішкі бөлігі Көпбұрыштын сыртқы
- 5. Егер көпбұрыштың төбелері кез келген қабырғасы
- 6. Төртбұрыш Әрбір төртбұрыштың :
- 7. Параллелограмм А В С
- 8. Параллелограмның белгілері
- 9. Трапеция Екі қабырғасы өзара параллель , ал
- 10. Егер бұрыштың қабырғаларын қиып өтетін параллель түзілер
- 11. Тіктөртбұрыш Барлық бұрыштары тік болатын төртбұрыш
- 12. Ромб АВ СD, АD ВС < A=
- 13. а Екі және
- 14. Фигура а түзуіне қарағанда симметриялы деп
- 15. Фигура О нүктесіне қарағанда симметриялы деп аталады,
- 16. Аудан ұғымы. Ауданның қасиеттері. Жазық пішіндерді
- 17. 1. Тең фигуралар аудандары тең болады.
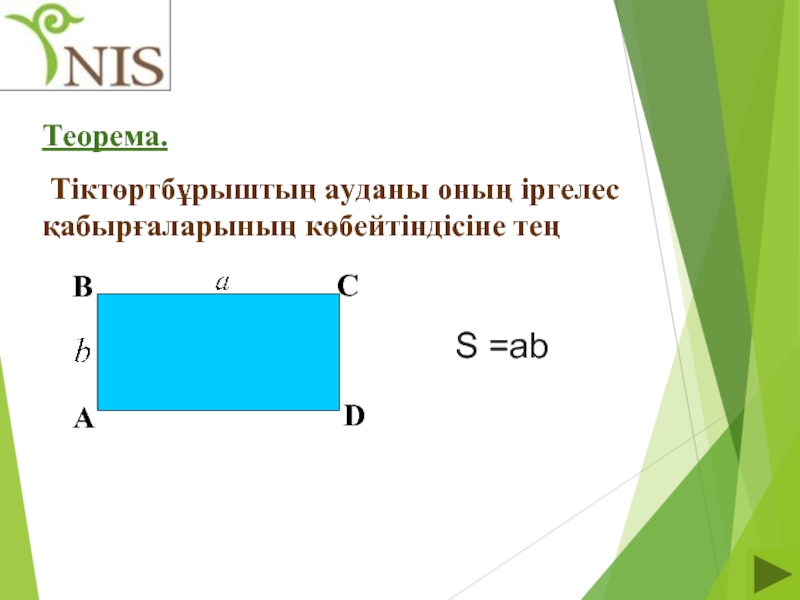
- 18. Теорема. Тіктөртбұрыштың ауданы оның іргелес қабырғаларының
- 19. Параллелограмм ауданы. Теорема. Параллелограмның ауданы оның қабырғасын
- 20. Үшбұрыштың ауданы. Теорема. Үшбұрыштың ауданы оның
- 21. Трапеция ауданы. Теорема. Трапецияның ауданы оның биіктігін табандарының жарым қосындысына көбейткенге тең.
- 22. Тікбұрышты үшбұрыштың гипотенузасының квадраты оның катеттерінің квадраттарының
- 23. Үшбұрыштар ұқсастығы
- 24. Теорема! I ұқсастық белгісі Егер бір үшбұрыштың
- 25. Теорема! III ұқсастық белгісі Егер бір үшбұрыштың
- 26. Үшбұрыштың орта сызығы деп екі қабырғасының
- 27. Үшбұрыштың орта сызығы оның бір қабырғасына параллель
- 28. Үшбұрыштың медианалары бір нүктеде қиылысады
- 29. Тікбұрышты үшбұрыштың тік бұрышынан гипотенузаға түсірілген биіктік
- 30. Тік бұрышты үшбұрыштың тік бұрышынан түсірілген биіктік,
- 31. Тікбұрышты үшбұрыштың катеті гипотенуза және тікбұрышты төбесінен
- 32. Тікбұрышты үшбұрыштың қабырғалары және бұрыштарының арасындағы қатынас
- 33. Тікбұрышты үшбұрыштың сүйір бұрышының синусы Тікбұрышты үшбұрыштың
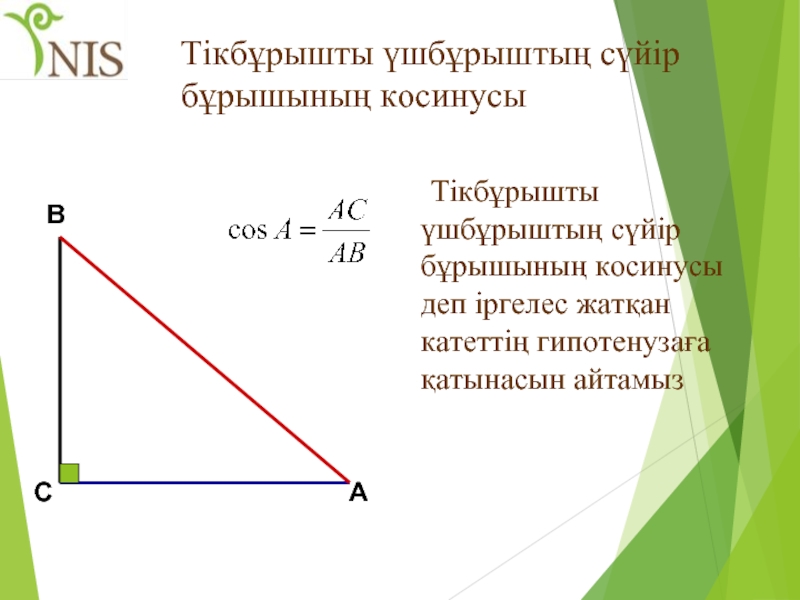
- 34. Тікбұрышты үшбұрыштың сүйір бұрышының косинусы Тікбұрышты үшбұрыштың
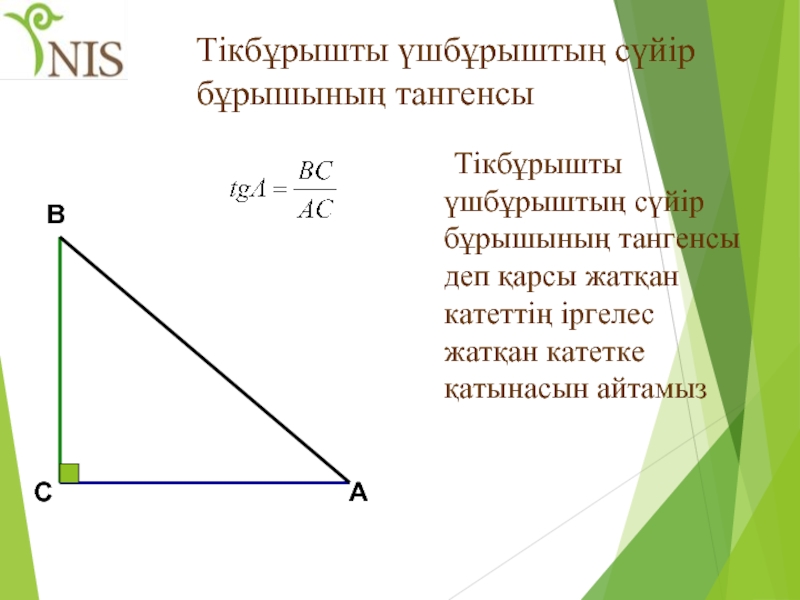
- 35. Тікбұрышты үшбұрыштың сүйір бұрышының тангенсы Тікбұрышты үшбұрыштың
- 36. Тригонометриялық теңбе-теңдіктер Негізгі тригонометриялық теңбң-теңдік
Слайд 2Мазмұны
Төртбұрыштар
Көпбұрыштар
Параллелограмм
Трапеция
Фалес теоремасы
Тіктөртбұрыш
Ромб
Остік және централік симметрия
Аудан
Ауданның қасиеттері
Тіктөртбұрыштың ауданы
Параллелограмның ауданы
Үшбұрыштың ауданы
Трапецияның ауданы
Пифагор теоремасы
Ұқсас үшбұрыштар
Ұқсас үшбұрыштар анықтамасы
Үшбұрыштардың ұқсастық белгілері
Үшбұрыштың орта сызығы
Тікбұрышты үшбұрыштың қабырғалары және бұрыштарының арасындағы қатынас
Слайд 3А
В
С
D
E
F
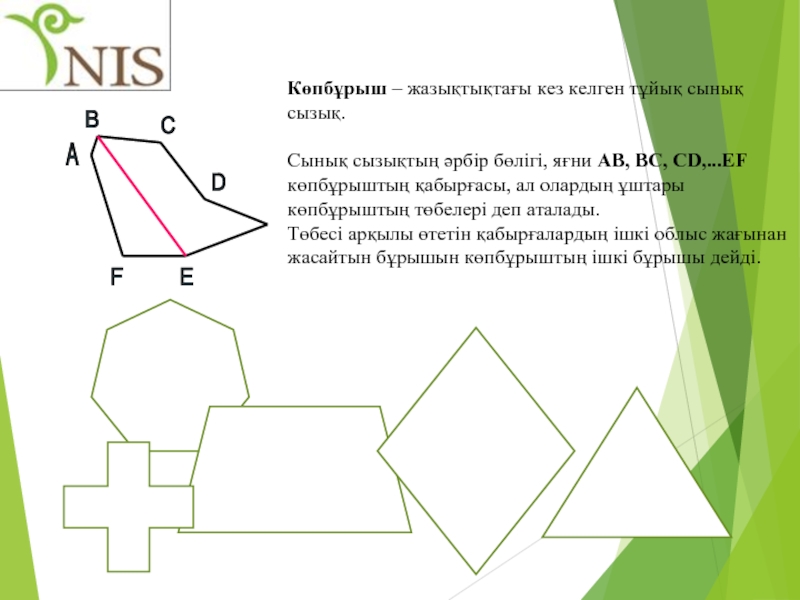
Көпбұрыш – жазықтықтағы кез келген тұйық
Сынық сызықтың әрбір бөлігі, яғни AB, BC, CD,...EF көпбұрыштың қабырғасы, ал олардың ұштары көпбұрыштың төбелері деп аталады.
Төбесі арқылы өтетін қабырғалардың ішкі облыс жағынан жасайтын бұрышын көпбұрыштың ішкі бұрышы дейді.
Слайд 4
Көпбұрыш ішкі бөлігі
Көпбұрыштын сыртқы бөлігі
(көпбұрыш жазықтығынан тыс жазықтық бөлігі)
(көпбұрыш
Слайд 5
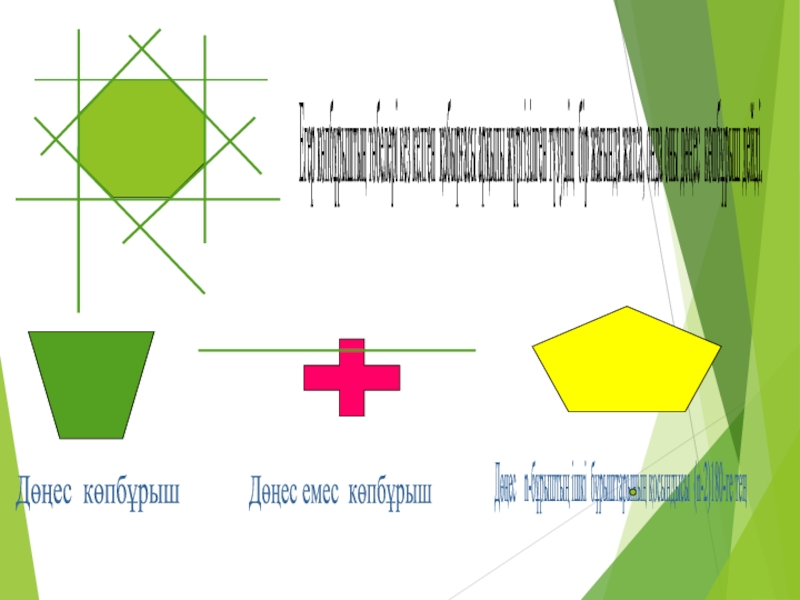
Егер көпбұрыштың төбелері кез келген қабырғасы арқылы жүргізілген түзудің бір жағында
Дөңес көпбұрыш
Дөңес емес көпбұрыш
Дөңес n-бұрыштың ішкі бұрыштарының қосындысы (n-2)180-ге тең
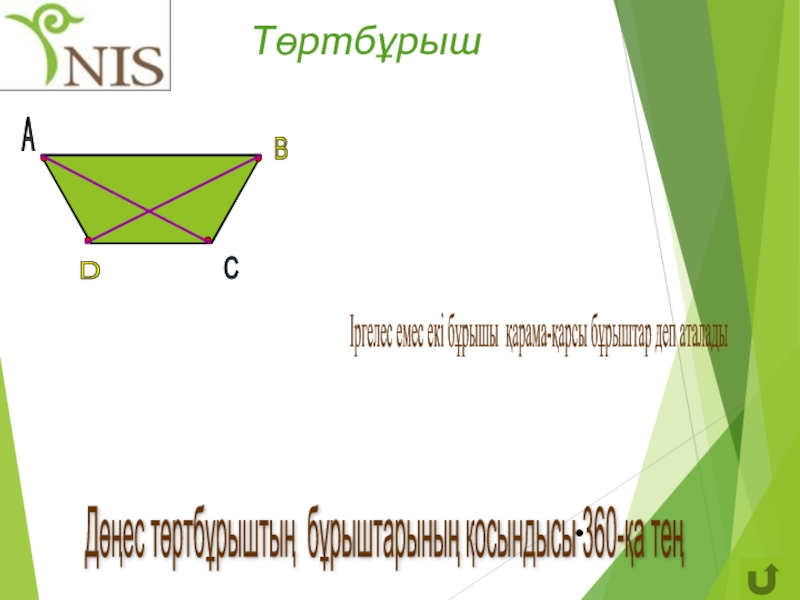
Слайд 6Төртбұрыш
Әрбір төртбұрыштың :
төрт төбесі,
төрт қабырғасы,
екі диагоналі бар
Іргелес
А
B
C
D
Дөңес төртбұрыштың бұрыштарының қосындысы 360-қа тең
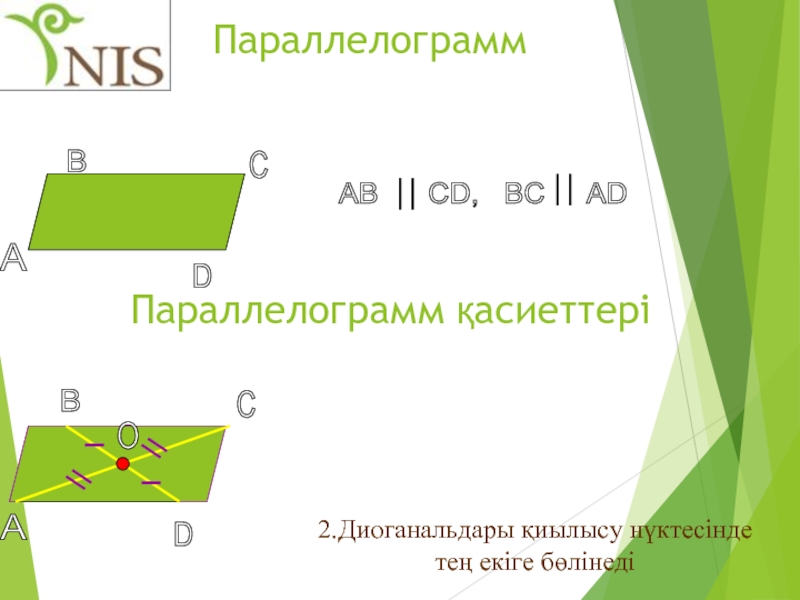
Слайд 7Параллелограмм
А
В
С
D
AB CD, BC
Параллелограмның қарама-қарсы
қабырғалары және қарама-қарсы бұрыштары тең .
AB=CD, BC=AD,
Параллелограмм қасиеттері Қарама-қарсы қабырғалары параллель
болатын төртбұрыш параллелограмм деп аталады.
. 2.Диоганальдары қиылысу нүктесінде тең екіге бөлінеді
Слайд 8Параллелограмның белгілері
Егер төртбұрыштың екі қабырғасы тең және параллель болса, онда
Егер төртбұрыштың қарама-қарсы қабырғалары қос-қостан тең болса, онда бұл төртбұрыш-параллелограмм.
Егер төртбұрыштың диагональдары қиылысып, қиылысу нүктесінде тең екіге бөлінетін болса, онда ол-параллелограмм.
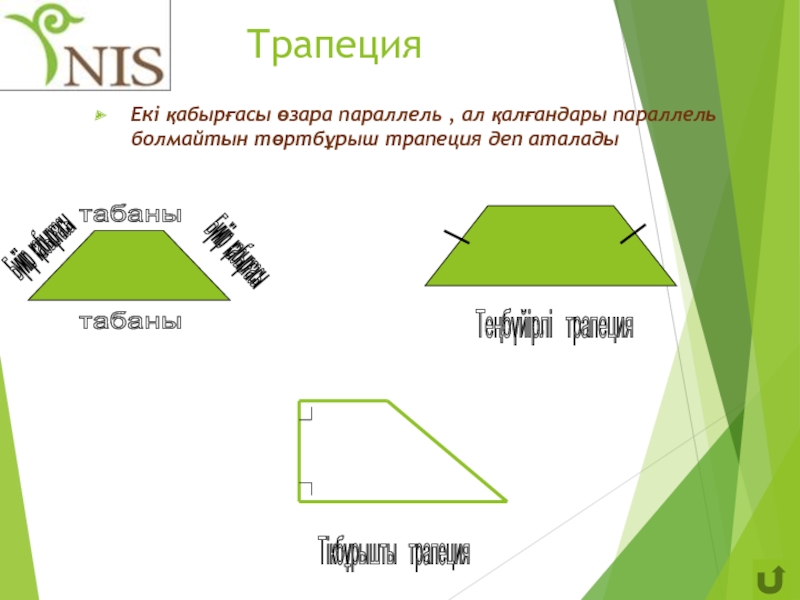
Слайд 9Трапеция
Екі қабырғасы өзара параллель , ал қалғандары параллель болмайтын төртбұрыш трапеция
табаны
табаны
Бүйір қабырғасы
Бүйір қабырғасы
Теңбүйірлі трапеция
Тікбұрышты трапеция
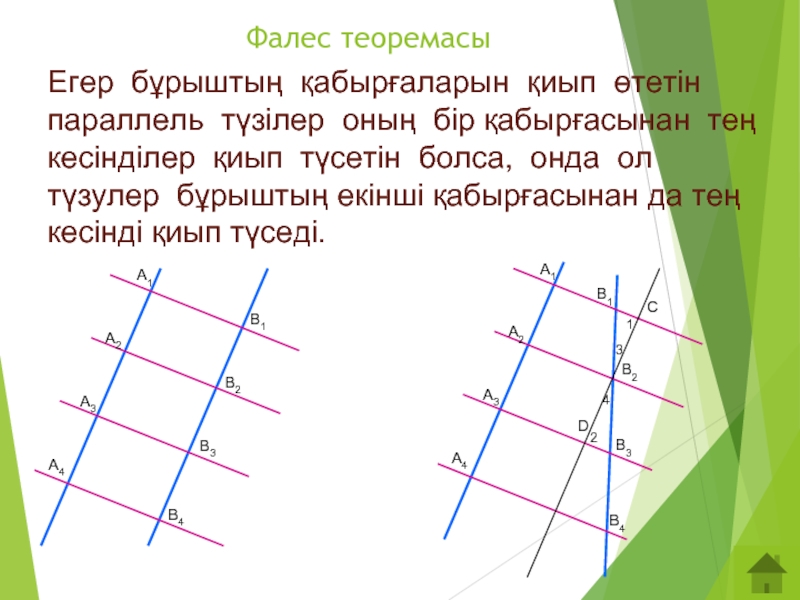
Слайд 10Егер бұрыштың қабырғаларын қиып өтетін параллель түзілер оның бір қабырғасынан тең
Фалес теоремасы
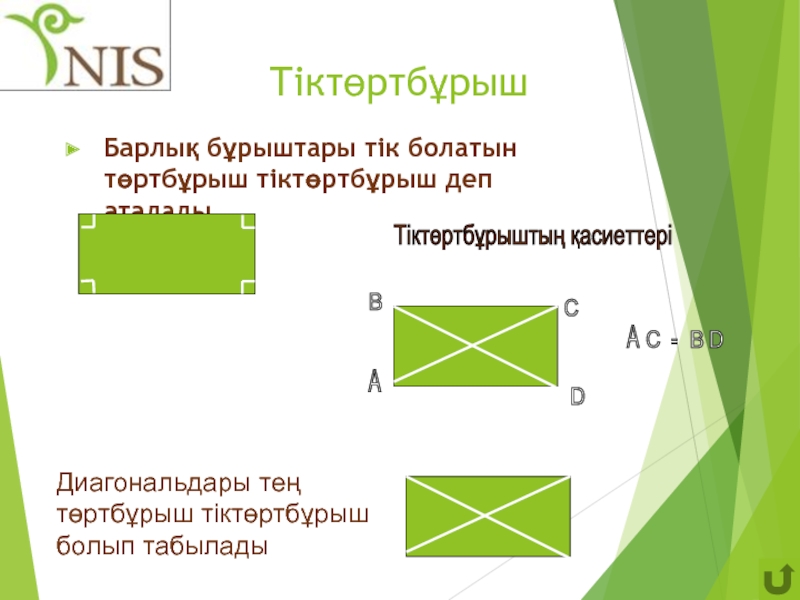
Слайд 11Тіктөртбұрыш
Барлық бұрыштары тік болатын төртбұрыш тіктөртбұрыш деп аталады.
Тіктөртбұрыштың қасиеттері
Диагональдары
А
В
С
D
Диагональдары тең төртбұрыш тіктөртбұрыш болып табылады
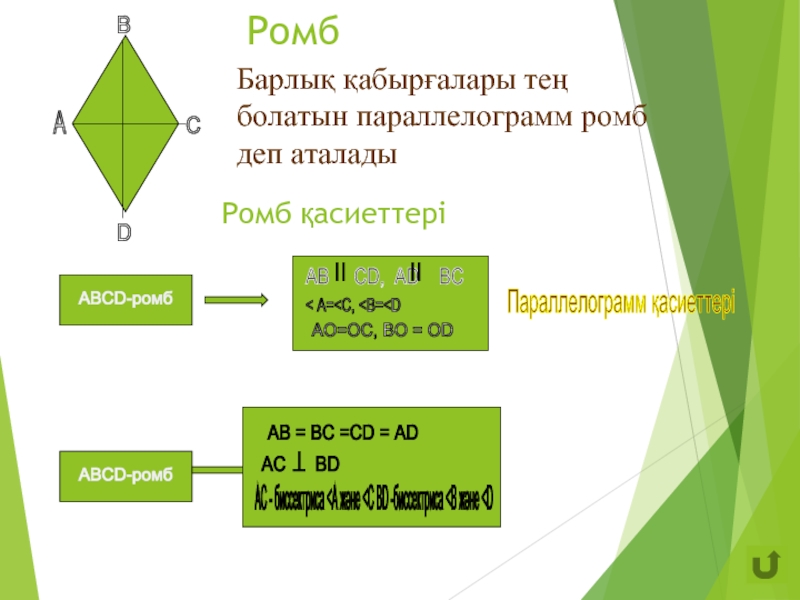
Слайд 12Ромб
АВ СD, АD ВС
< A=
AO=OC, BO = OD
Параллелограмм қасиеттері
Барлық қабырғалары тең
Диагональдары перпендикуляр
Әрбір диагоналі бұрыштың
биссектрисасы
А
В
D
С
Барлық қабырғалары тең
болатын параллелограмм ромб
деп аталады
Ромб қасиеттері
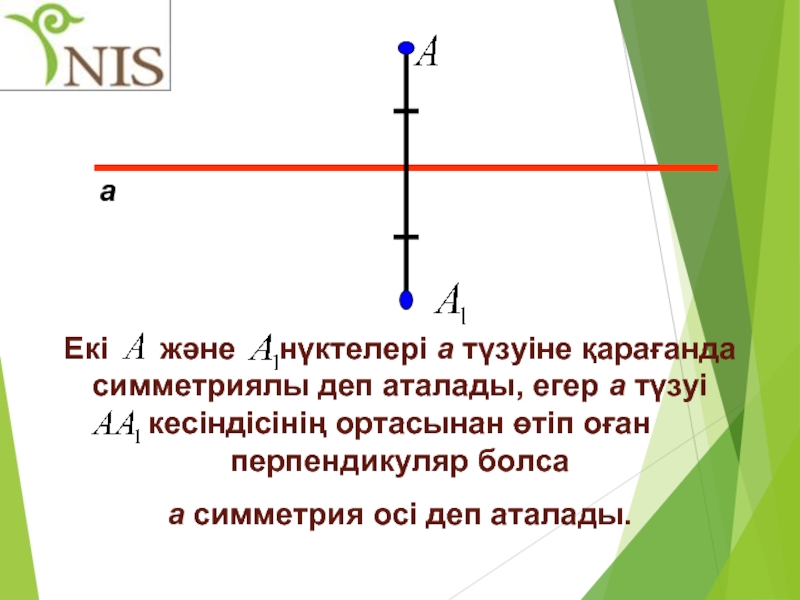
Слайд 13а
Екі және нүктелері а түзуіне қарағанда симметриялы
а симметрия осі деп аталады.
Слайд 14
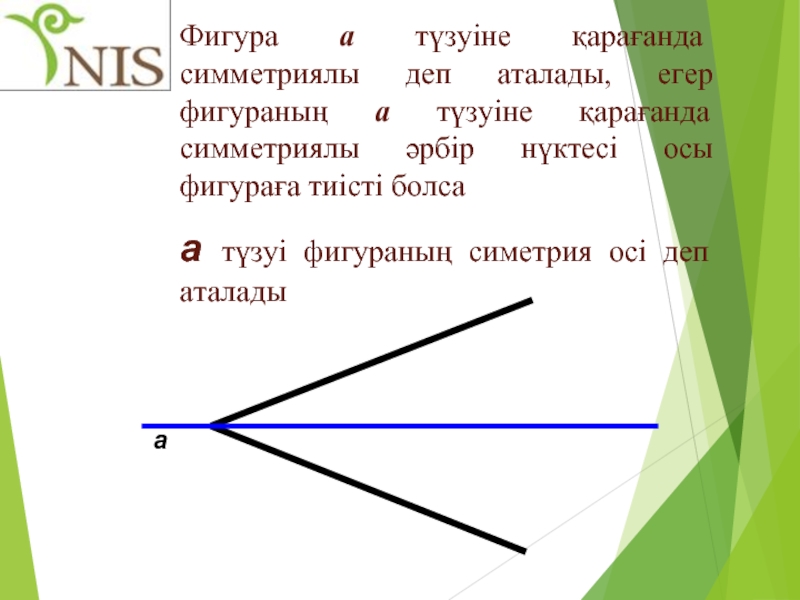
Фигура а түзуіне қарағанда симметриялы деп аталады, егер фигураның а түзуіне
а түзуі фигураның симетрия осі деп аталады
а
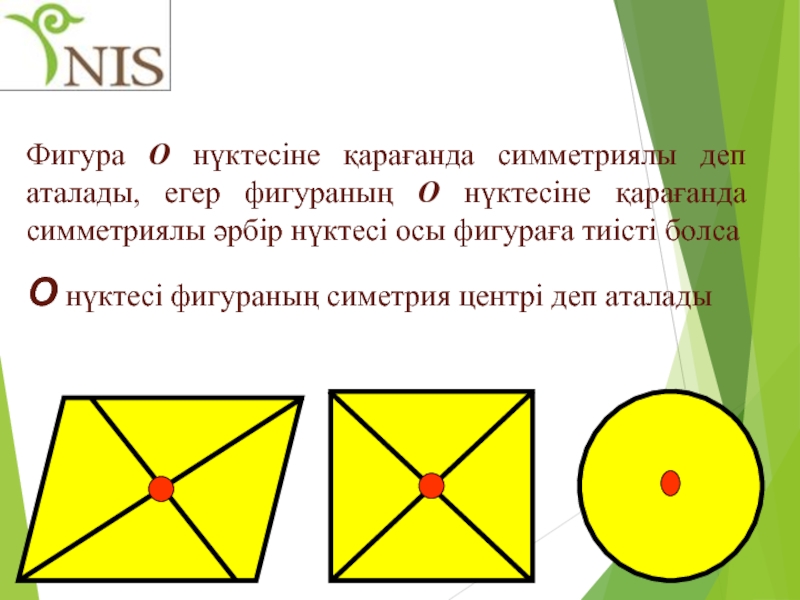
Слайд 15Фигура О нүктесіне қарағанда симметриялы деп аталады, егер фигураның О нүктесіне
О нүктесі фигураның симетрия центрі деп аталады
Слайд 16 Аудан ұғымы. Ауданның қасиеттері.
Жазық пішіндерді қамтитын бірлік квадраттардың (қабырғалары ұзындықтың
Слайд 171. Тең фигуралар аудандары тең болады.
2. Егер фигура бөліктерге бөлінсе ,
Аудан ұғымы.
Ауданның қасиеттері.
Слайд 19Параллелограмм ауданы.
Теорема. Параллелограмның ауданы оның қабырғасын сол қабырғаға түсірілген биіктіктің көбейтіндісіне
a
b
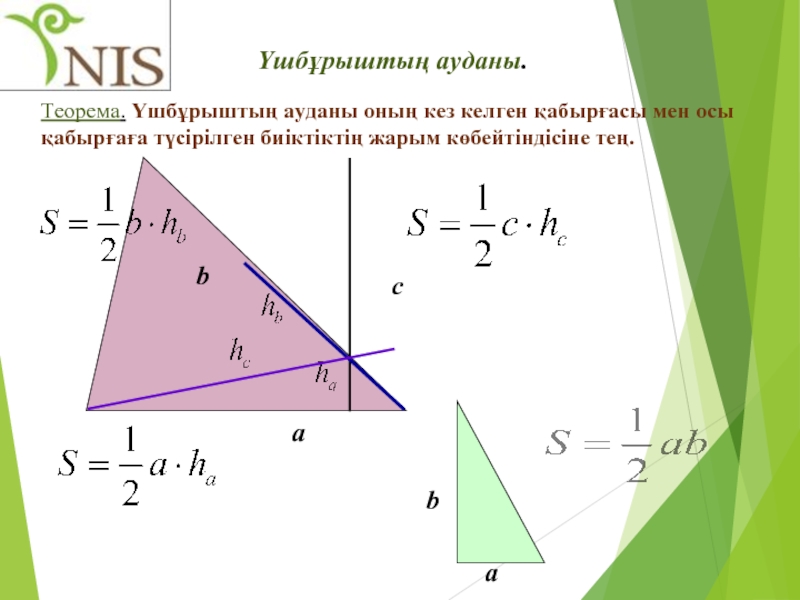
Слайд 20 Үшбұрыштың ауданы.
Теорема. Үшбұрыштың ауданы оның кез келген қабырғасы мен осы
a
b
c
b
a
Слайд 21 Трапеция ауданы.
Теорема. Трапецияның ауданы оның биіктігін табандарының жарым қосындысына көбейткенге
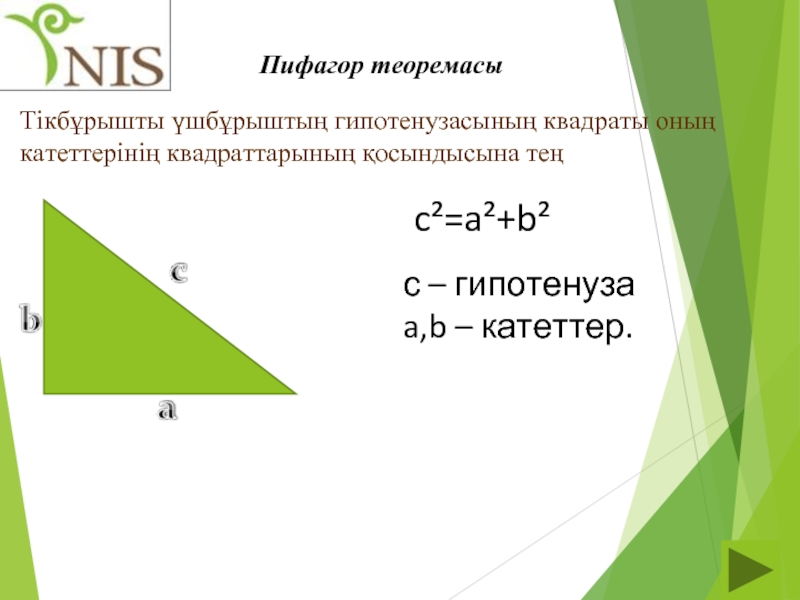
Слайд 22Тікбұрышты үшбұрыштың гипотенузасының квадраты оның катеттерінің квадраттарының қосындысына тең
c²=a²+b²
с – гипотенуза
a,b
Пифагор теоремасы
Слайд 23Үшбұрыштар ұқсастығы
С
А
В
A1
C1
B1
AB и A1B1, BC и B1C1, AC и A1C1 –
Екі үшбұрыш ұқсас болып табылады, егер олардың сәйкес бұрыштары тең және қабырғалары пропорционал болса.
Слайд 24Теорема!
I ұқсастық белгісі
Егер бір үшбұрыштың екі бұрышы екінші үшбұрыштың екі бұрышына
II ұқсастық белгісі
Егер бір үшбұрыштың екі қабырғасы екінші үшбұрыштың екі қабырғасына пропорционал және олардың арасындағы бұрыштар тең болса, онда бұл үшбұрыштар ұқсас.
Слайд 25Теорема!
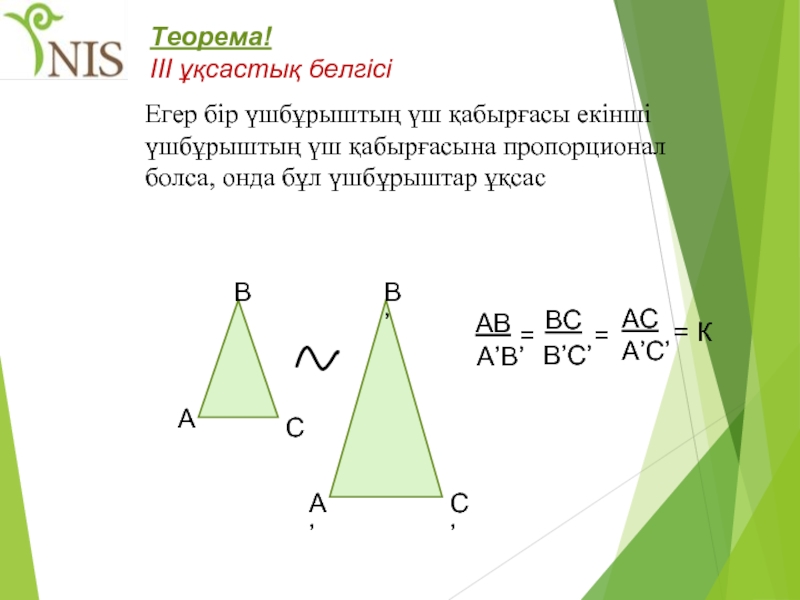
III ұқсастық белгісі
Егер бір үшбұрыштың үш қабырғасы екінші үшбұрыштың үш қабырғасына
АВ
A’B’
=
BС
B’C’
AC
A’C’
=
= К
В
А
С
A’
B’
C’
Слайд 26
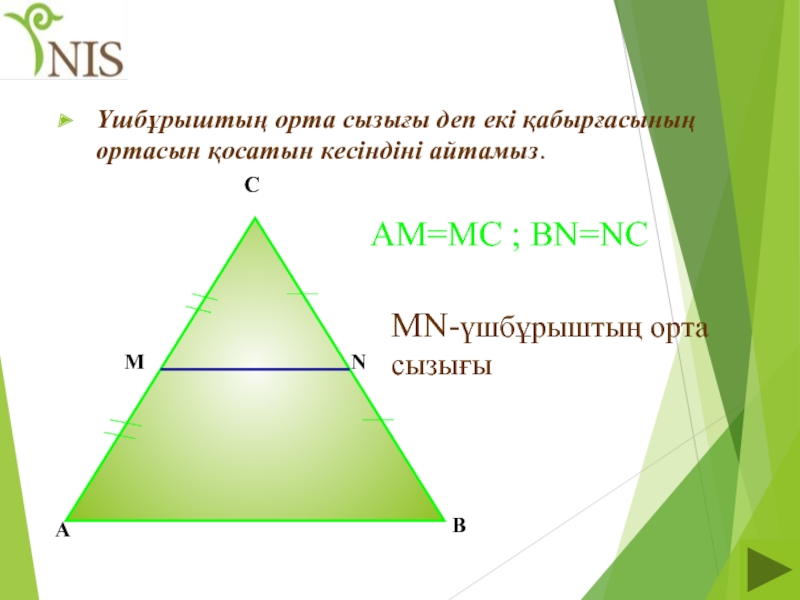
Үшбұрыштың орта сызығы деп екі қабырғасының ортасын қосатын кесіндіні айтамыз.
А
В
С
М
N
AM=MC ;
MN-үшбұрыштың орта сызығы
Слайд 27Үшбұрыштың орта сызығы оның бір қабырғасына параллель және ұзындығы оның жартысына
А
В
С
M
N
1
2
Слайд 28 Үшбұрыштың медианалары бір нүктеде қиылысады және қиылысу нүктесінде төбесінен
А
В
С
С1
В1
А1
О
АО:ОА1=ВО:ОВ1=
=СО:ОС1=2:1
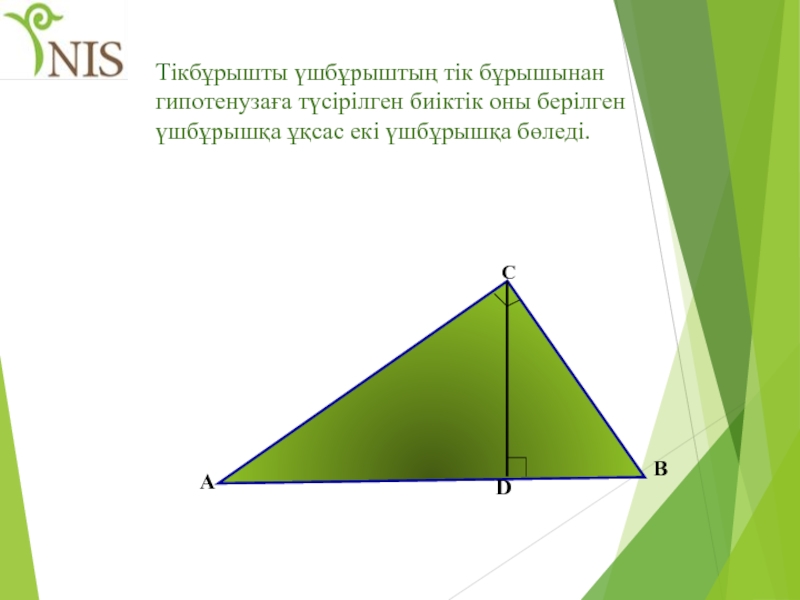
Слайд 29Тікбұрышты үшбұрыштың тік бұрышынан гипотенузаға түсірілген биіктік оны берілген үшбұрышқа ұқсас
А
С
В
D
Слайд 30Тік бұрышты үшбұрыштың тік бұрышынан түсірілген биіктік, гипотенузаның бойынан бөлінетін кесінділер
А
С
В
D
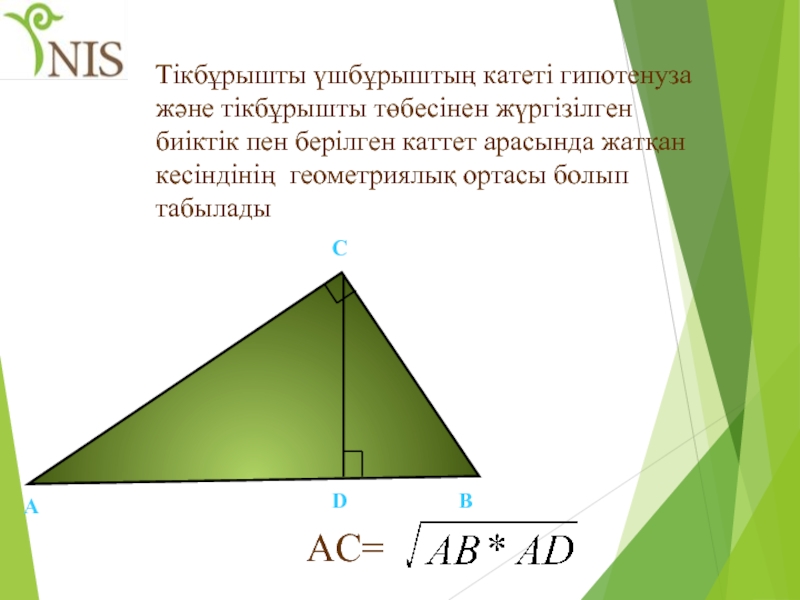
Слайд 31Тікбұрышты үшбұрыштың катеті гипотенуза және тікбұрышты төбесінен жүргізілген биіктік пен берілген
А
В
С
D
AC=
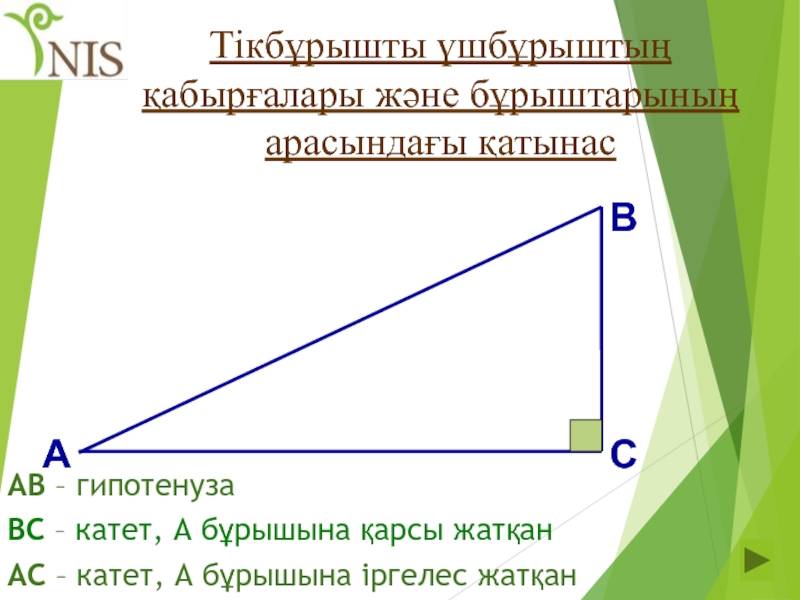
Слайд 32Тікбұрышты үшбұрыштың қабырғалары және бұрыштарының арасындағы қатынас
А
В
С
АВ – гипотенуза
ВС – катет,
АС – катет, А бұрышына іргелес жатқан
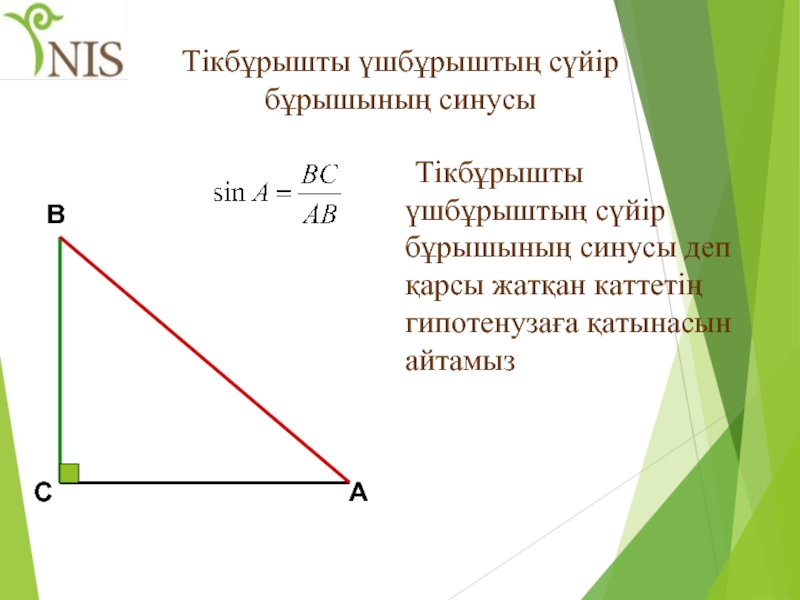
Слайд 33Тікбұрышты үшбұрыштың сүйір бұрышының синусы
Тікбұрышты үшбұрыштың сүйір бұрышының синусы деп қарсы
В
С
А
Слайд 34Тікбұрышты үшбұрыштың сүйір бұрышының косинусы
Тікбұрышты үшбұрыштың сүйір бұрышының косинусы деп іргелес
В
С
А
Слайд 35Тікбұрышты үшбұрыштың сүйір бұрышының тангенсы
Тікбұрышты үшбұрыштың сүйір бұрышының тангенсы деп қарсы
В
С
А