- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрические построения и приемы работы чертежными инструментами презентация
Содержание
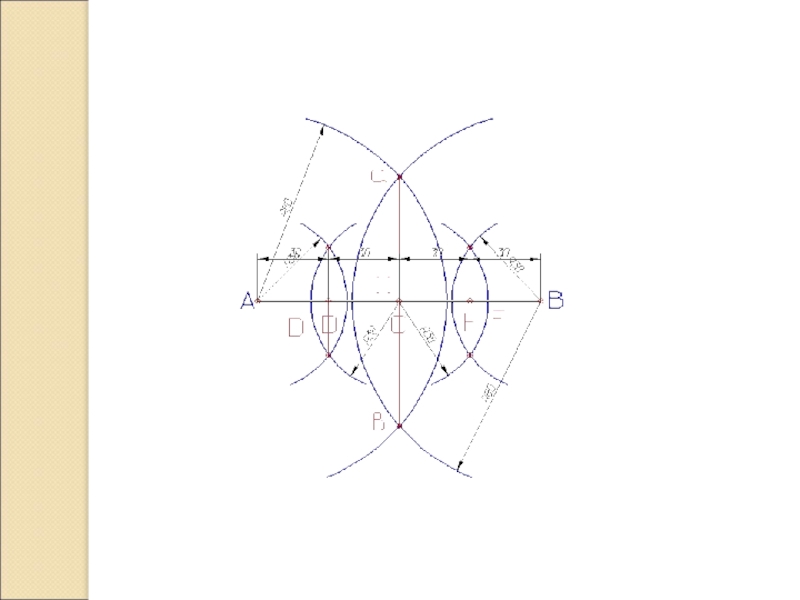
Слайд 3Деление отрезка на 2 и 4 части.
Из концов отрезка А и В циркулем проводят две дуги окружности радиусом R, несколько большим половины отрезка, до взаимного пересечения в точках а и в.
Через полученные точки а и в проведем прямую, которая пересекает отрезок АВ в точке С, делящей отрезок на две равные части.
Проделав подобные построения для отрезков АС и СВ, получим точки D и F. Точки С, D и F делят отрезок АВ на четыре равные части.
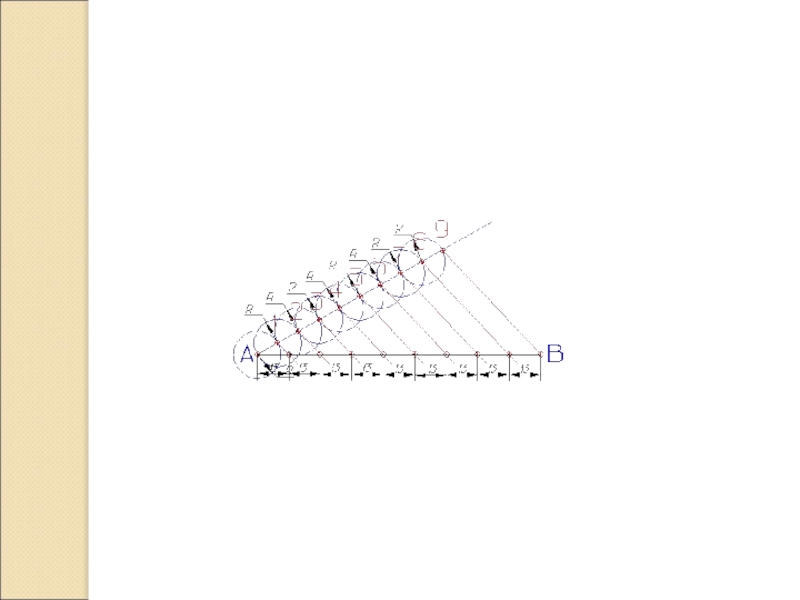
Слайд 5Деление отрезка на n частей.
Пусть отрезок АВ требуется разделить
на 9 равных частей.
Для этого из любого конца отрезка (из точки А) проведем под острым углом к отрезку прямую линию, на которой от точки А измерительным циркулем откладываем 9-ть равных отрезков произвольной величины.
Точку 9 соединяем с точкой В (концом данного отрезка) прямой.
Из точек 1, 2, ... 8 проведем ряд прямых параллельных прямой 9А, которые пересекая отрезок АВ разделят его на 9 равных частей.
Для этого из любого конца отрезка (из точки А) проведем под острым углом к отрезку прямую линию, на которой от точки А измерительным циркулем откладываем 9-ть равных отрезков произвольной величины.
Точку 9 соединяем с точкой В (концом данного отрезка) прямой.
Из точек 1, 2, ... 8 проведем ряд прямых параллельных прямой 9А, которые пересекая отрезок АВ разделят его на 9 равных частей.
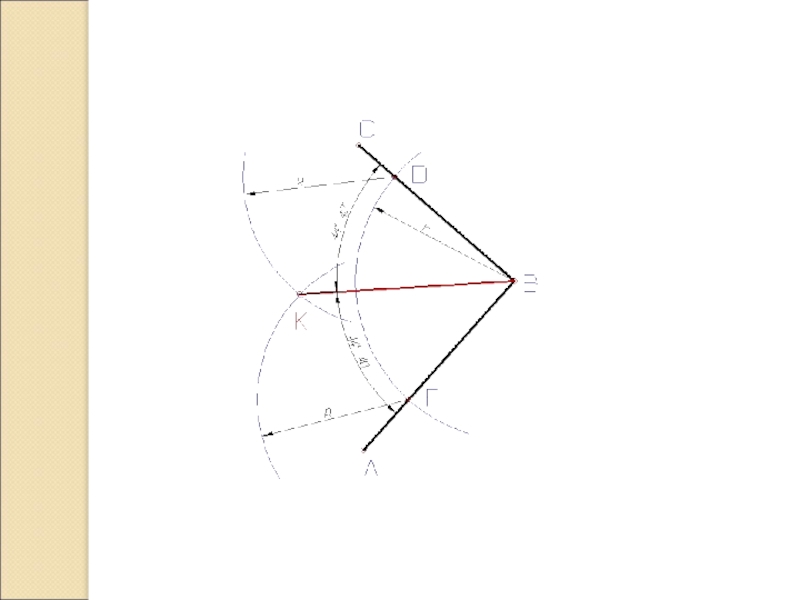
Слайд 7Деление угла на 2 части.
Для того чтобы разделить
угол АВС пополам нужно провести биссектрису из вершины угла. Построение биссектрисы выполняется в следующей последовательности:
Из вершины угла проводят дугу окружности произвольного радиуса r до пересечения со сторонами угла в точках D и F;
Из полученных точек проводят две дуги радиусом R, величина которого больше половины длины дуги DF, до взаимного пересечения в точке К;
Прямая проходящая через вершину В и точку К - биссектриса данного угла т.е. делит угол на две равные части.
Из вершины угла проводят дугу окружности произвольного радиуса r до пересечения со сторонами угла в точках D и F;
Из полученных точек проводят две дуги радиусом R, величина которого больше половины длины дуги DF, до взаимного пересечения в точке К;
Прямая проходящая через вершину В и точку К - биссектриса данного угла т.е. делит угол на две равные части.
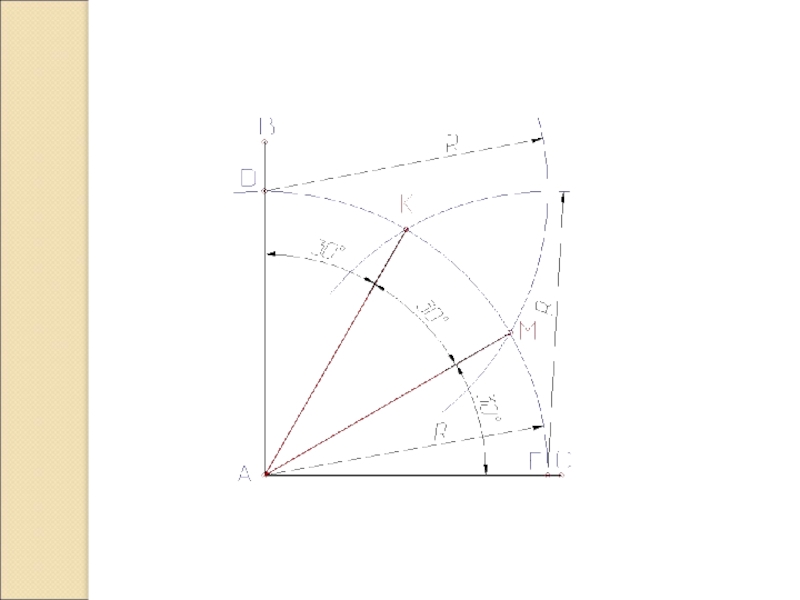
Слайд 9Деление прямого угла на 3 части.
Деление прямого угла АВС
на три равные части выполняется в следующей последовательности:
Из вершины угла проводят дугу окружности произвольного радиуса R до пересечения со сторонами угла в точках D и F;
Из полученных точек проводят две дуги тем же радиусом R, до взаимного пересечения с дугой DF в точках К и М;
Точки К и М соединяют с вершиной В прямыми, которые разделят угол АВС на три равные части.
Из вершины угла проводят дугу окружности произвольного радиуса R до пересечения со сторонами угла в точках D и F;
Из полученных точек проводят две дуги тем же радиусом R, до взаимного пересечения с дугой DF в точках К и М;
Точки К и М соединяют с вершиной В прямыми, которые разделят угол АВС на три равные части.