ОБРАЗОВАНИЯ
«САРАТОВСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ Н.Г. ЧЕРНЫШЕВСКОГО»
Кафедра дискретной математики и
информационных технологий
ГЕОМЕТРИЧЕСКИЕ ОБРАЗЫ АВТОМАТНЫХ ОТОБРАЖЕНИЙ
КУРСОВАЯ РАБОТА
Студентки 3 курса 321 группы
направления 09.03.01 — Информатика и вычислительная техника
факультета КНиИТ
Бобковой Дианы Андреевны
Научный руководитель
к. ф.-м.н., доцент Тяпаев Л. Б.
Саратов 2016
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрические образы, автоматных отображений презентация
Содержание
- 1. Геометрические образы, автоматных отображений
- 2. ЦЕЛЬ РАБОТЫ Проведение вычислительных экспериментов, а именно,
- 3. БАЗОВЫЕ ПОНЯТИЯ
- 4. БАЗОВЫЕ ПОНЯТИЯ
- 5. АВТОМАТНЫЕ ОТОБРАЖЕНИЯ, ЗАДАННЫЕ С ПОМОЩЬЮ ГЕОМЕТРИЧЕСКИХ ОБРАЗОВ
- 6. Реализация построений автоматных отображений, заданных с помощью
- 7. Реализация построений автоматных отображений, заданных с помощью геометрических образов
- 8. Реализация построений автоматных отображений, заданных с помощью геометрических образов
- 9. Реализация построений автоматных отображений, заданных с помощью геометрических образов
- 10. Реализация построений автоматных отображений, заданных с помощью геометрических образов
- 11. Реализация построений автоматных отображений, заданных с помощью геометрических образов
- 12. Реализация построений автоматных отображений, заданных с помощью геометрических образов
- 13. ВЫВОД В результате выполнения данного курсового проекта
- 14. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 1. Л. Б. Тяпаев.
- 15. БЛАГОДАРЮ ЗА ВНИМАНИЕ!
ЦЕЛЬ РАБОТЫ Проведение вычислительных экспериментов, а именно, построение проекций автоматных отображений Евклидовой плоскости, представленными геометрическими образами – множествами точек с рациональными координатами. ЗАДАЧА Реализация программы и исследование разнообразия графиков, полученных данным
Слайд 1Министерство образования и науки Российской Федерации
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
Слайд 2ЦЕЛЬ РАБОТЫ
Проведение вычислительных экспериментов, а именно, построение проекций автоматных отображений Евклидовой
плоскости, представленными геометрическими образами – множествами точек с рациональными координатами.
ЗАДАЧА
Реализация программы и исследование разнообразия графиков, полученных данным способом автоматных отображений
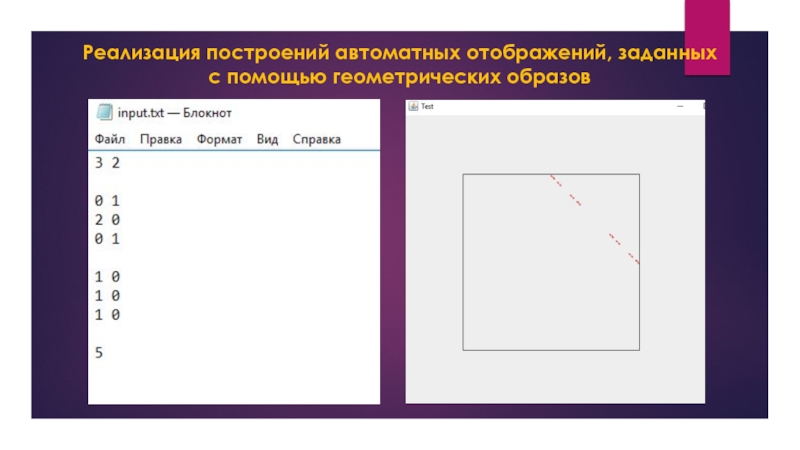
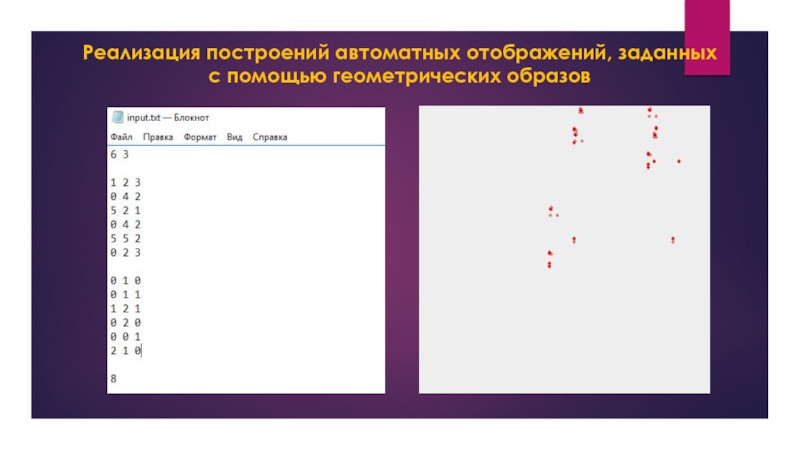
Слайд 6Реализация построений автоматных отображений, заданных с помощью геометрических образов
Алгоритм работы программы:
Программа
считывает автомат в виде:
— количество заданных состояний;
— количество входов и выходов;
— таблица переходов;
— таблица выходов;
— желаемая длина последовательности.
Генерируются всевозможные последовательности заданной длины.
Каждая из сгенерированных последовательностей пропускается через автомат поразрядно, справа налево.
Выходные последовательности записываются аналогично поразрядно справа налево.
Далее по формуле считаются координаты.
Полученные координаты точек отмечаются на графике.
— количество заданных состояний;
— количество входов и выходов;
— таблица переходов;
— таблица выходов;
— желаемая длина последовательности.
Генерируются всевозможные последовательности заданной длины.
Каждая из сгенерированных последовательностей пропускается через автомат поразрядно, справа налево.
Выходные последовательности записываются аналогично поразрядно справа налево.
Далее по формуле считаются координаты.
Полученные координаты точек отмечаются на графике.
Слайд 13ВЫВОД
В результате выполнения данного курсового проекта был разработан программный продукт, при
помощи которого можно увидеть точечный график.
Было проведено исследование полученного программного продукта. В результате были рассмотрены разнообразные графики, полученные при работе программы.
В целом, поставленная в начале курсового проекта цель была достигнута. В программе выполняются все необходимые функциональные требования.
Было проведено исследование полученного программного продукта. В результате были рассмотрены разнообразные графики, полученные при работе программы.
В целом, поставленная в начале курсового проекта цель была достигнута. В программе выполняются все необходимые функциональные требования.
Слайд 14СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Л. Б. Тяпаев. Решение некоторых задач для конечных
автоматов. // Известия Саратовского ун-та. Нов. Серия. Серия Математика. Механика. Информатика, 2006. — 6(1-2) — C. 121-133.
2. З.И. Боревич, И.Р. Шафаревич. Теория чисел. — М.: Наука. Главная редакция физико-математической литературы.— 1985.— 504 с., 3-е изд.доп.
3. Р. Р. Энгелькинг. Общая топология. — М.: Мир, 1986. — 752 с.
4. V. Anashin, A. Krennikov. Applied algebraic dynamics. Walter de Gruyter GmbH & Co., Berlin–N.Y., 2009.
5. R. I. Grigorchuk, V. V. Nekrashevich, and V. I. Sushchanskii. Automata, dynamical systems, and groups. Proc. Steklov Institute Math., 231:128—203, 2000.
6. Л. Б. Тяпаев. Геометрическая модель поведения автоматов и их неотличимость // Математика. Механика. — Изд-во Сар. ун-та, 1999. — C. 139-143.
7. Л. Б. Тяпаев. Геометрические образы автоматов и динамические системы// Материалы X Международного семинара "Дискретная математика и её приложения".— М.: Изд-во мех.-мат. факультета МГУ, 2010. — C.510-513.
8. Л. Б. Тяпаев. Д. Б. Василенко. Дискретные динамические системы, определяемые геометрическими образами автоматов . // Интеллектуальные системы. — 2013. — 17(1-4). — C. 196-201.
2. З.И. Боревич, И.Р. Шафаревич. Теория чисел. — М.: Наука. Главная редакция физико-математической литературы.— 1985.— 504 с., 3-е изд.доп.
3. Р. Р. Энгелькинг. Общая топология. — М.: Мир, 1986. — 752 с.
4. V. Anashin, A. Krennikov. Applied algebraic dynamics. Walter de Gruyter GmbH & Co., Berlin–N.Y., 2009.
5. R. I. Grigorchuk, V. V. Nekrashevich, and V. I. Sushchanskii. Automata, dynamical systems, and groups. Proc. Steklov Institute Math., 231:128—203, 2000.
6. Л. Б. Тяпаев. Геометрическая модель поведения автоматов и их неотличимость // Математика. Механика. — Изд-во Сар. ун-та, 1999. — C. 139-143.
7. Л. Б. Тяпаев. Геометрические образы автоматов и динамические системы// Материалы X Международного семинара "Дискретная математика и её приложения".— М.: Изд-во мех.-мат. факультета МГУ, 2010. — C.510-513.
8. Л. Б. Тяпаев. Д. Б. Василенко. Дискретные динамические системы, определяемые геометрическими образами автоматов . // Интеллектуальные системы. — 2013. — 17(1-4). — C. 196-201.
