- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Генеральная совокупность и выборка презентация
Содержание
- 1. Генеральная совокупность и выборка
- 2. При изучении реальных явлений часто бывает
- 3. - объем генеральной совокупности - объем репрезентативной выборки - частоты - частоты в генеральной совокупности
- 4. Для идеально составленной репрезентативной выборки должно выполняться
- 5. Пример 1 Фабрика резиновых изделий
- 6. N=100 солдат (объем репрезентативной выборки)
- 7. Размах и центральные тенденции
- 8. 1. Размах, мода и медиана
- 9. Нужно сравнить интерес к чтению
- 10. Размах (обозначается R) — разница между наибольшим
- 12. Пример 1. Вычислить размах, моду
- 13. Средним значением случайной величины X
- 14. Если значения случайной величины Xl,Х2,...,Xk
- 15. Подчёркнем, что существует возможность измерить, охарактеризовать
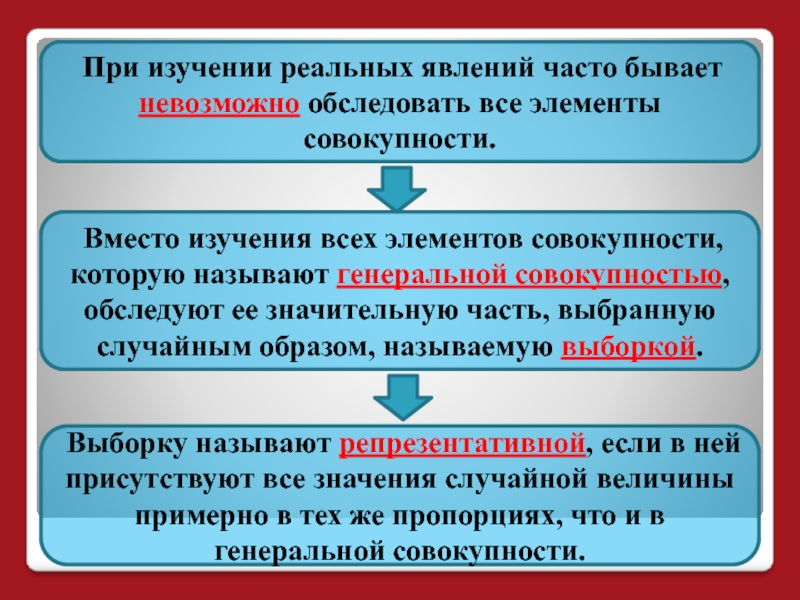
Слайд 2 При изучении реальных явлений часто бывает невозможно обследовать все элементы
Вместо изучения всех элементов совокупности, которую называют генеральной совокупностью, обследуют ее значительную часть, выбранную случайным образом, называемую выборкой.
Выборку называют репрезентативной, если в ней присутствуют все значения случайной величины примерно в тех же пропорциях, что и в генеральной совокупности.
Слайд 3- объем генеральной совокупности
- объем репрезентативной выборки
- частоты
- частоты в генеральной
Слайд 4Для идеально составленной репрезентативной выборки должно выполняться равенство:
Где i – порядковый
Слайд 5Пример 1
Фабрика резиновых изделий выиграла тендер на изготовление
Сколько противогазов каждого размера будет изготавливать фабрика?
Слайд 6N=100 солдат (объем репрезентативной выборки)
- объем генеральной совокупности
Количество противогазов соответствующего размера можно найти по формуле (2).
Слайд 81. Размах, мода и медиана
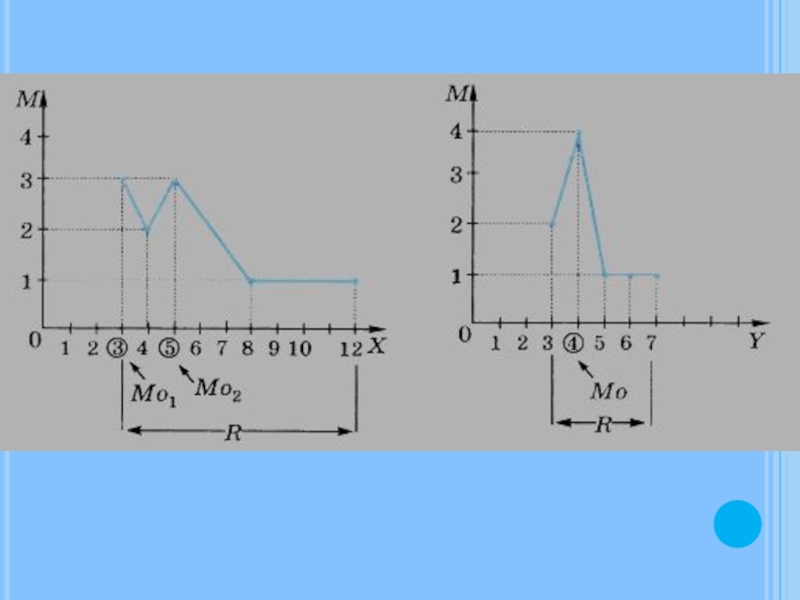
Имеются:
1) распределение
2) распределение по частотам случайной величины У — числа прочитанных за каникулы книг девятью мальчиками того же класса.
Слайд 9 Нужно сравнить интерес к чтению девочек и мальчиков этого
Для сравнения предложенных совокупностей могут быть использованы различные характеристики. Перечислим некоторые из них.
Выпишем последовательность:
3, 3, 3, 4, 4, 5, 5, 5, 8, 12
3, 3, 4, 4, 4, 4, 5, 6, 7.
Слайд 10Размах (обозначается R) — разница между наибольшим и наименьшим значениями случайной
Мода (обозначим Мо) — наиболее часто встречающееся значение случайной величины.
Медиана (обозначим Me) — это так называемое серединное значение упорядоченного ряда значений случайной величины.
Слайд 12Пример 1.
Вычислить размах, моду и медиану для последовательности:
-2, 3, 4, -3, 0, 1, 3, -2, -1, 2, -2, 1.
Слайд 13 Средним значением случайной величины X (обозначается ) называют
Если все значения случайной величины X1, Х2,…,ХN различны, то
2. Среднее значение
Слайд 14 Если значения случайной величины Xl,Х2,...,Xk имеют в совокупности соответственно
Зная, что , формулу (4) можно переписать в виде
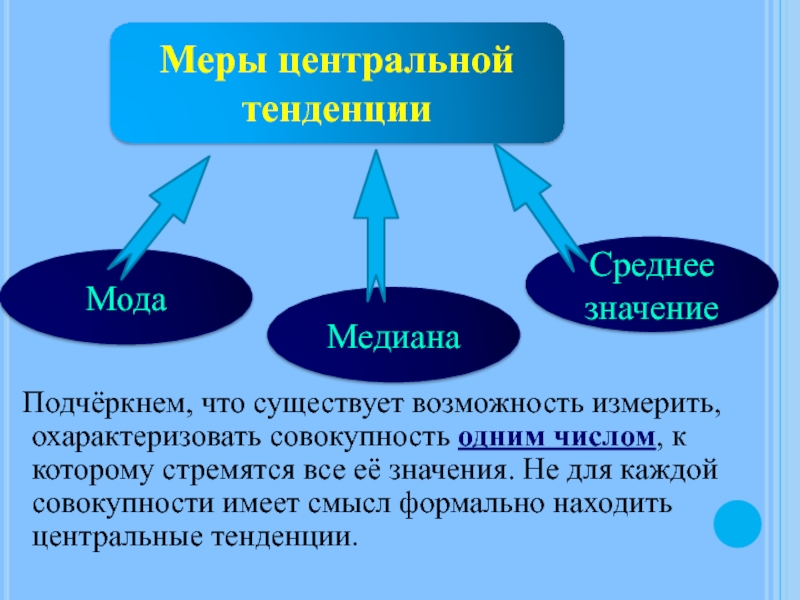
Слайд 15 Подчёркнем, что существует возможность измерить, охарактеризовать совокупность одним числом, к
Мода
Медиана
Среднее значение
Меры центральной тенденции