- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Циліндр, його елементи. Переріз площинами презентация
Содержание
- 2. Циліндр, його елементи. Переріз площинами
- 4. План: Тіла обертання Означення циліндра Елементи циліндра Перерізи циліндра Площа поверхні циліндра Розв’язування задач
- 5. Ніколи ще до нашого часу ми не
- 6. Тіла та поверхні обертання
- 8. Циліндр - грец. κύλινδρος — валик
- 11. Осьовий переріз циліндра — прямокутник зі сторонами,
- 12. Види циліндрів
- 13. ОСЬОВИЙ ПЕРЕРІЗ Якщо січна площина
- 14. Теорема 1: Переріз циліндра площиною, паралельною його
- 15. КРУГОВИЙ ПЕРЕРІЗ Круговий переріз –
- 16. Теорема 2: Переріз циліндра площиною, паралельною основам
- 17. Переріз циліндра площиною, паралельною його осі (KLMN)
- 18. ПРЯМИЙ КРУГОВИЙ ЦИЛІНДР Циліндр називається прямим,
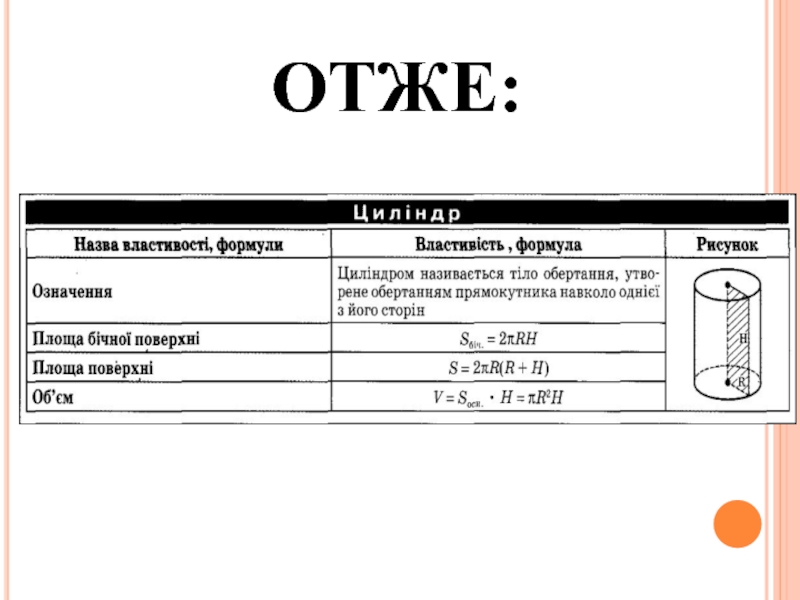
- 19. Площа поверхні циліндра Площа повної поверхні
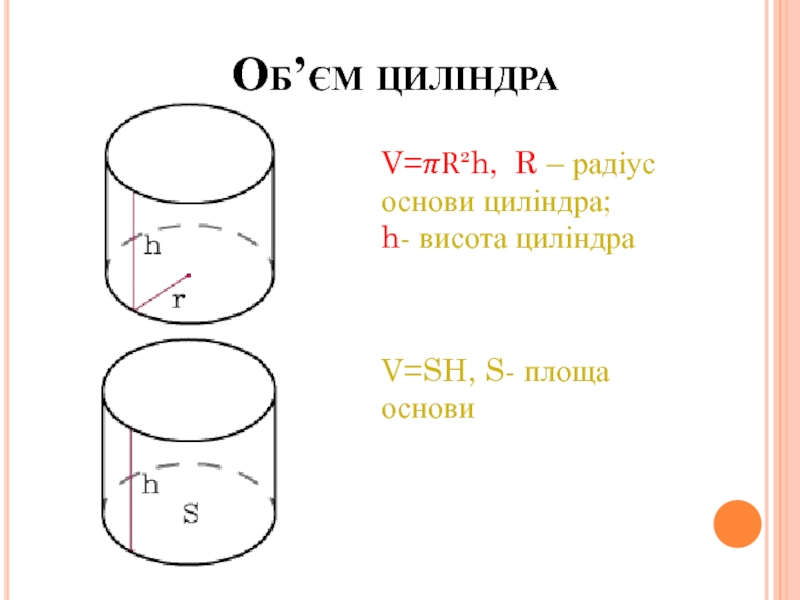
- 20. Об’єм циліндра V=?R²h, R – радіус основи
- 21. ДОТИЧНА ПЛОЩИНА ДО ЦИЛІНДРА Дотичною
- 22. Використання циліндрів
- 25. Задача №2 Висота циліндра дорівнює 7 см,
- 27. ОТЖЕ:
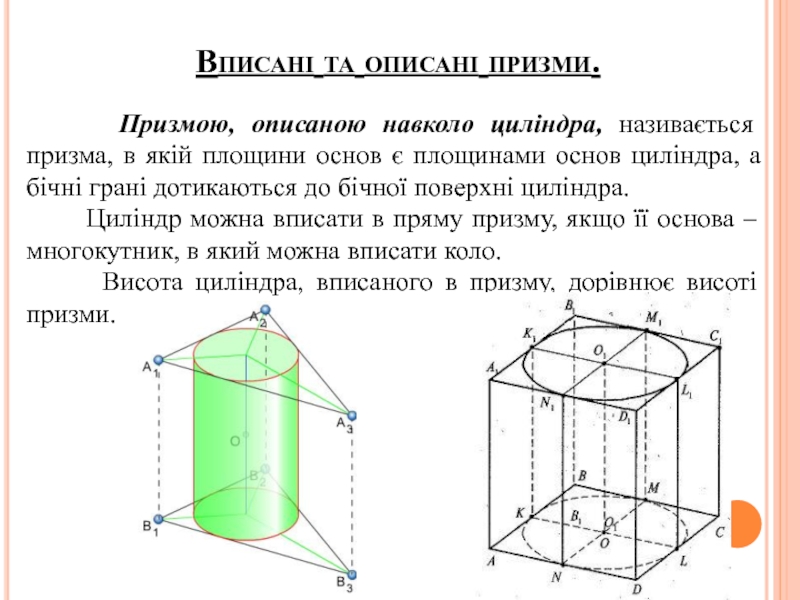
- 29. Вписані та описані призми.
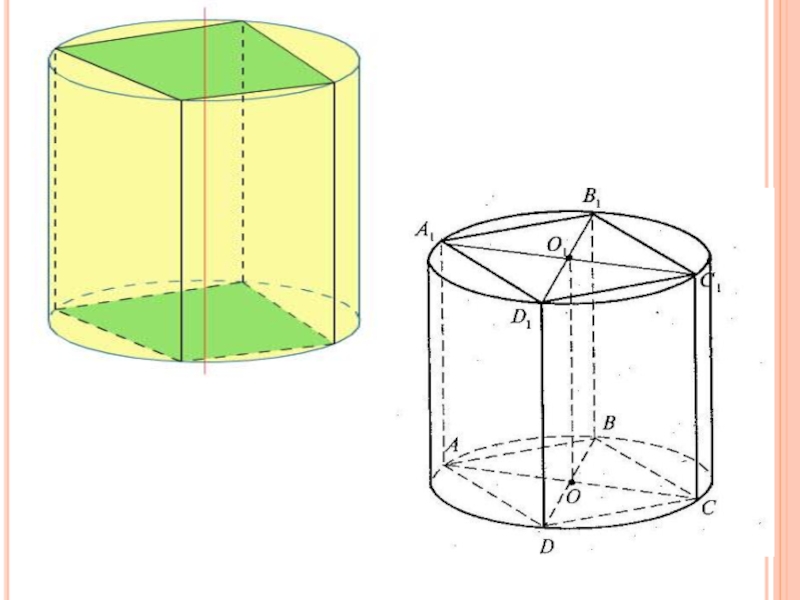
- 30. Призмою, вписаною в циліндр, називається
- 32. Циліндр вписаний в призму Знайдемо відношення
- 33. Зокрема, відношення об'єму правильної трикутної призми до
- 36. Циліндр описаний навколо призми Знайдемо відношення
- 38. Формули обчислення радіусу R описаного кола, а,b,c
- 39. Формули обчислення радіусу r вписаного кола
Слайд 4План:
Тіла обертання
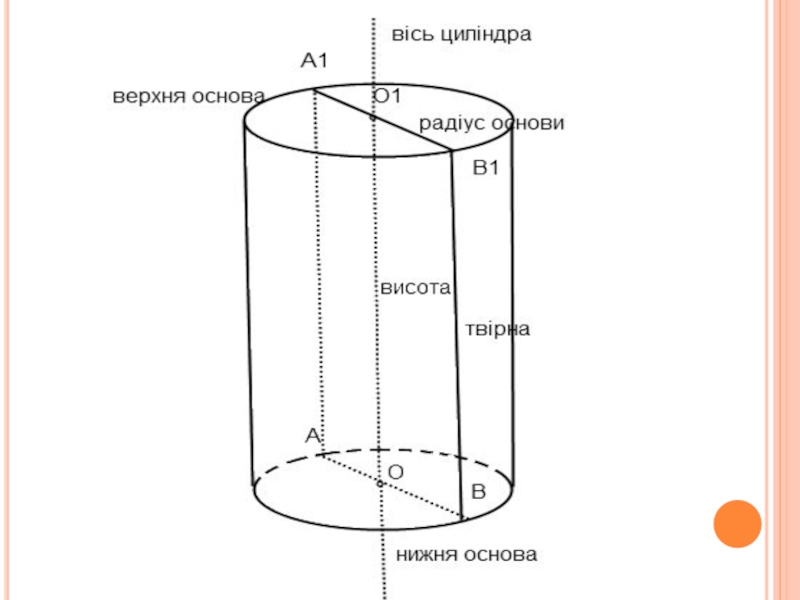
Означення циліндра
Елементи циліндра
Перерізи циліндра
Площа поверхні циліндра
Розв’язування задач
Слайд 5Ніколи ще до нашого часу ми не жили в такий геометричний
Навколишній світ – це світ геометрії, чистий, істинний, бездоганний у наших очах. Все навколо - геометрія.
Ле Корбюзьє
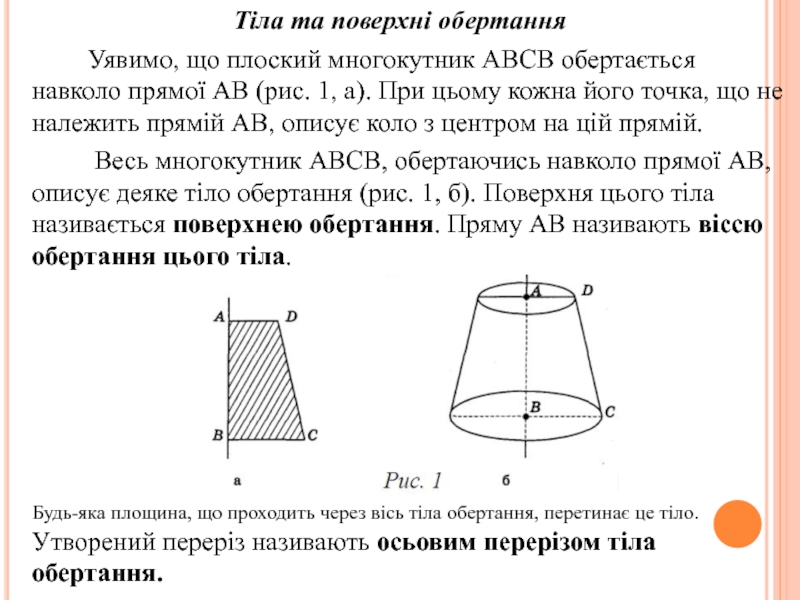
Слайд 6Тіла та поверхні обертання
Уявимо, що
Весь многокутник АВСВ, обертаючись навколо прямої АВ, описує деяке тіло обертання (рис. 1, б). Поверхня цього тіла називається поверхнею обертання. Пряму АВ називають віссю обертання цього тіла.
Будь-яка площина, що проходить через вісь тіла обертання, перетинає це тіло. Утворений переріз називають осьовим перерізом тіла обертання.
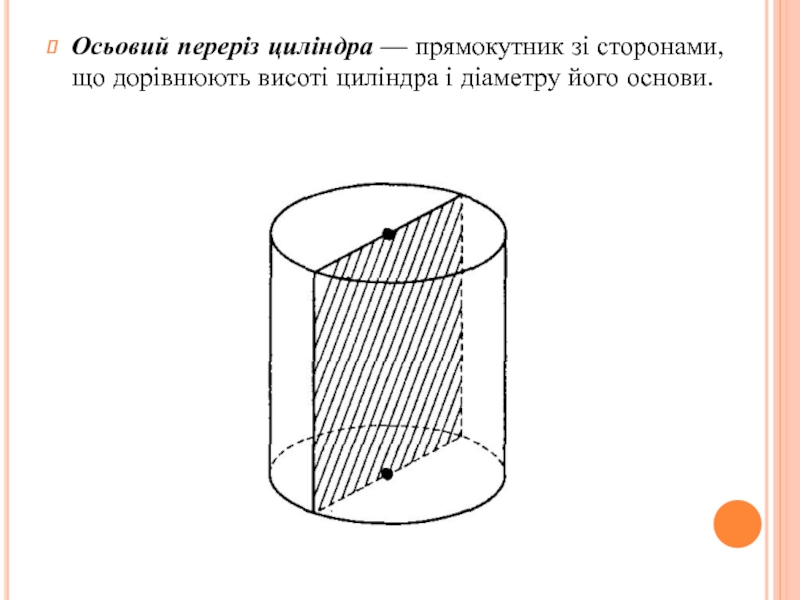
Слайд 11Осьовий переріз циліндра — прямокутник зі сторонами, що дорівнюють висоті циліндра
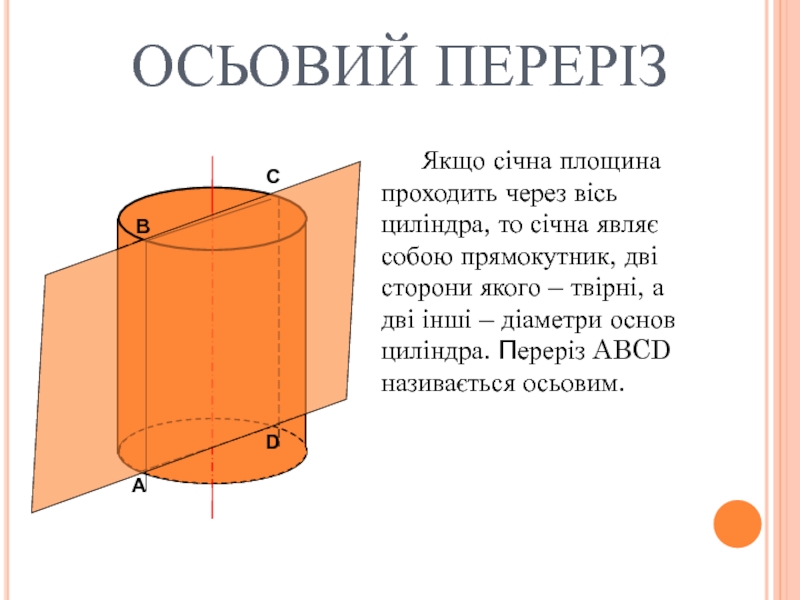
Слайд 13ОСЬОВИЙ ПЕРЕРІЗ
Якщо січна площина проходить через вісь циліндра, то січна
A
D
C
B
Слайд 14Теорема 1: Переріз циліндра площиною, паралельною його осі, є прямокутник.
Доведення:
Слайд 15КРУГОВИЙ ПЕРЕРІЗ
Круговий переріз – це переріз циліндра площиною, паралельною його
С
О
γ
α
Слайд 16Теорема 2: Переріз циліндра площиною, паралельною основам циліндра, є круг, який
Доведення:
Дійсно, січна площина перетинає циліндр по кругу, бо, якщо виконати паралельне перенесення уздовж осі циліндра, яке суміщає січну площину з площиною основи циліндра, то переріз суміститься з кругом.
Слайд 17Переріз циліндра площиною, паралельною його осі
(KLMN) || AB
KLMN – прямокутник
NK і
NK – висота циліндра
A
B
M
K
L
N
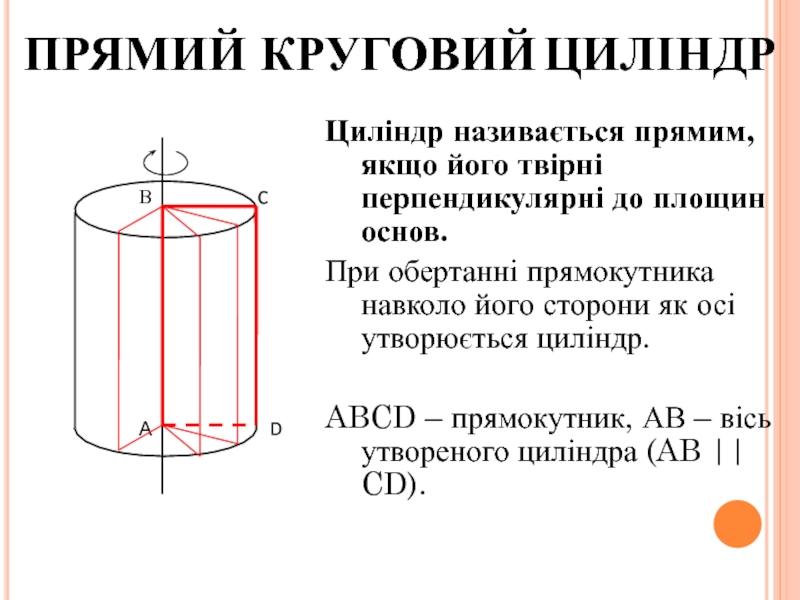
Слайд 18ПРЯМИЙ КРУГОВИЙ ЦИЛІНДР
Циліндр називається прямим, якщо його твірні перпендикулярні до площин
При обертанні прямокутника навколо його сторони як осі утворюється циліндр.
ABCD – прямокутник, АВ – вісь утвореного циліндра (AB || CD).
D
C
А
В
Слайд 19Площа поверхні циліндра
Площа повної поверхні циліндра дорівнює сумі площ його
Площа бічної поверхні циліндра обчислюється за формулою:
R
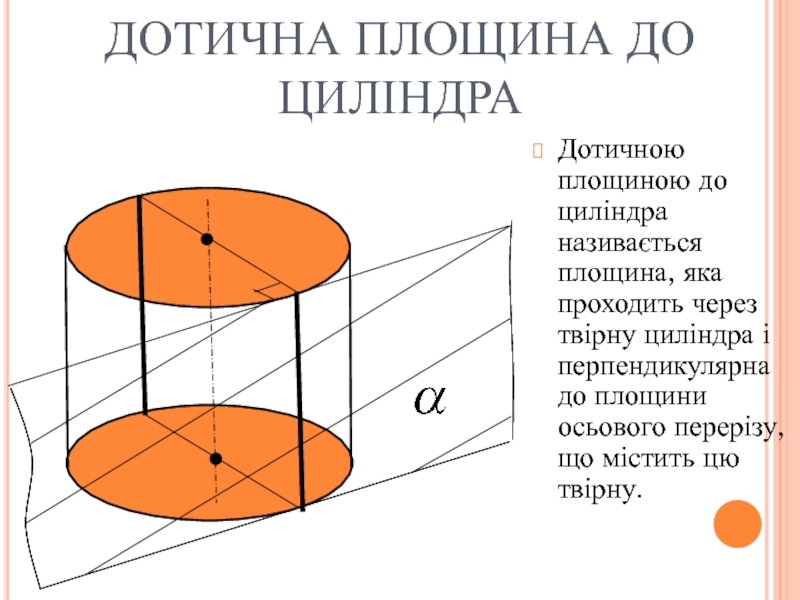
Слайд 21ДОТИЧНА ПЛОЩИНА ДО ЦИЛІНДРА
Дотичною площиною до циліндра називається площина, яка
Слайд 23 Задача №1 В циліндр площа основи дорівнює Q, а площа
Розв’язанння:
Відповідь:
D
A
C
O1
O
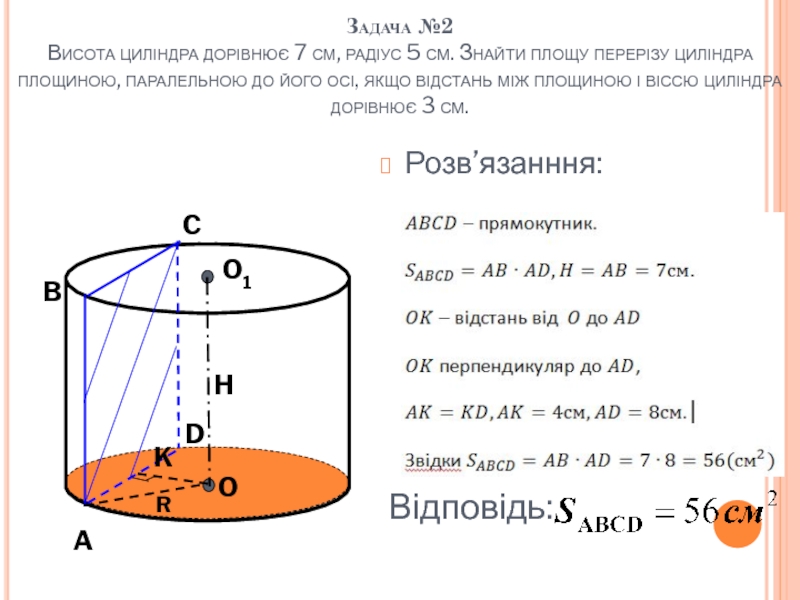
Слайд 25Задача №2 Висота циліндра дорівнює 7 см, радіус 5 см. Знайти площу
Розв’язанння:
Відповідь:
O
O1
A
B
C
D
K
H
R
Слайд 29Вписані та описані призми.
Призмою, описаною навколо циліндра, називається
Циліндр можна вписати в пряму призму, якщо її основа – многокутник, в який можна вписати коло.
Висота циліндра, вписаного в призму, дорівнює висоті призми.
Слайд 30 Призмою, вписаною в циліндр, називається призма, в якій площинами
Призму можна вписати в циліндр, якщо вона пряма та її основа – многокутник, який можна вписати в коло. Висота циліндра, описаного навколо призми, дорівнює висоті призми.
Слайд 32Циліндр вписаний в призму Знайдемо відношення об'єму призми до об'єму вписаного в
Слайд 33Зокрема, відношення об'єму правильної трикутної призми до об'єму вписаного циліндра Відношення об'єму
Слайд 36Циліндр описаний навколо призми
Знайдемо відношення об'єму призми до об'єму описаного навколо
Зокрема, відношення об'єму правильної трикутної призми до об'єму описаного циліндра
Відношення об'єму правильної чотирикутної призми (тобто прямокутного паралелепіпеда, в підставі якого лежить квадрат) до об'єму описаного біля неї циліндра рівне
Відношення об'єму правильної шестикутної призми до об'єму описаного біля неї циліндра