- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функцияның шегі. Қасиеті презентация
Содержание
- 1. Функцияның шегі. Қасиеті
- 2. Анықтама f функциясы x0 нүктесінің маңайында
- 3. Шектің қасиеті егер f (x) және g (x) функциялары шегі бар
- 4. Функцияның нүктедегі шегін есептеу мысалдары 1 2 3
- 5. Анықталмаған жағдайларды ашу Шектерді есептеу барысында келесі
- 6. Жалпы ереже: егер бөлшектің алымы мен бөлімінде көпмүшеліктер,
- 8. Алымы мен бөлімін түйіндес өрнекке көбейту әдісі
- 9. Тамаша шектер Бірінші тамаша шек
Анықтама f функциясы x0 нүктесінің маңайында анықталсын. f функциясы x0 нүктесінде шегі болады, егер x0 нүктесіне ұмтылатын xn (n = 1, 2,..., xn ≠ x0 ) нүктелер тізбегі үшін, f (xn) функция мәндерінің тізбегі А санына
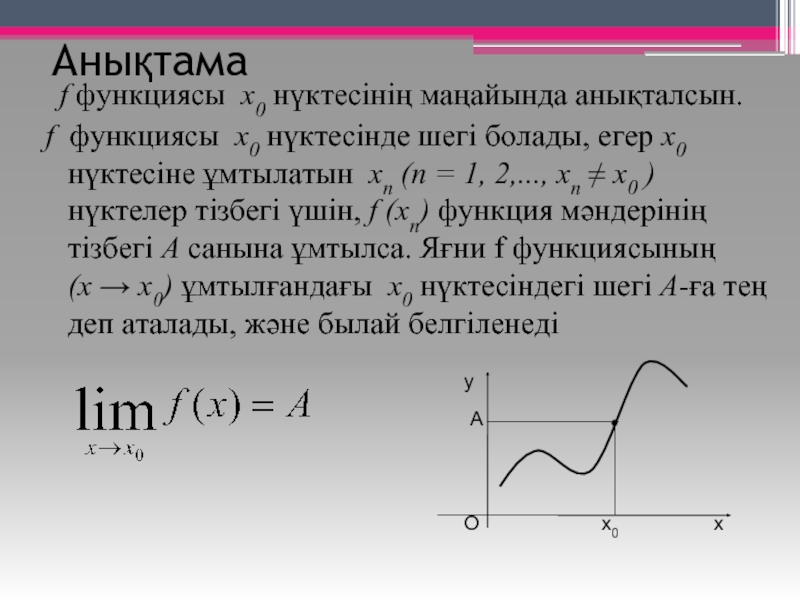
Слайд 2Анықтама
f функциясы x0 нүктесінің маңайында анықталсын.
f функциясы x0 нүктесінде шегі
болады, егер x0 нүктесіне ұмтылатын xn (n = 1, 2,..., xn ≠ x0 ) нүктелер тізбегі үшін, f (xn) функция мәндерінің тізбегі А санына ұмтылса. Яғни f функциясының (x → x0) ұмтылғандағы x0 нүктесіндегі шегі А-ға тең деп аталады, және былай белгіленеді
Слайд 3Шектің қасиеті
егер f (x) және g (x) функциялары шегі бар болса,
Онда
егер B ≠ 0 және егер g (x) ≠ 0
Слайд 5Анықталмаған жағдайларды ашу
Шектерді есептеу барысында келесі анықталмаған жағдайлармен кездесеміз
Осы жағдайларда шекті
есептеу анықталмағандықты ашу деп аталады. Нәтижесінде нақты сан, ноль немесе шексіздік шығуы мүмкін
∞/∞ түріндегі анықталмағандықты ашу үшін, айнымалының жоғарғы дәрежесіне алымы мен бөлімін бөлу жеткілікті
Слайд 6Жалпы ереже: егер бөлшектің алымы мен бөлімінде көпмүшеліктер, және 0/0 түріндегі анықталмаған
жағдай болса, онда оны ашу үшін бөлшектің алымы мен бөлімін көбейткіштерге жіктеу керек.
:
Слайд 8Алымы мен бөлімін түйіндес өрнекке көбейту әдісі
Егер бөлшектің алымы (бөлімінде) иррационал
өрнек болса, одан құтылу үшін бөлшектің алымы (бөлімін) түйіндес өрнекке көбейту керек
