- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Эконометрика. Нелинейная парная регрессия (НПР) презентация
Содержание
- 1. Эконометрика. Нелинейная парная регрессия (НПР)
- 2. План: Общие сведения о нелинейных парных регрессионных
- 3. 1. Общие сведения о нелинейных парных регрессионных моделях
- 4. Различают два класса нелинейных регрессий: регрессии,
- 5. Регрессии, нелинейные относительно фактора
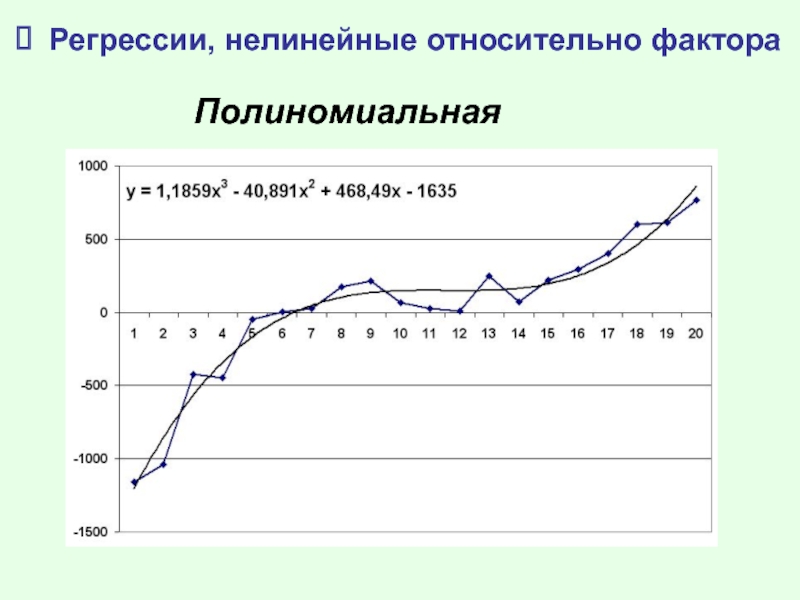
- 6. Регрессии, нелинейные относительно фактора Полиномиальная
- 7. Регрессии, нелинейные относительно фактора Применение полиномиальных моделей
- 8. Регрессии, нелинейные относительно фактора Применение гиперболических моделей
- 9. Кривая Филлипса Х – общий уровень безработицы
- 10. Кривая Филлипса Олбан Уильям Филлипс (1914-1975) -
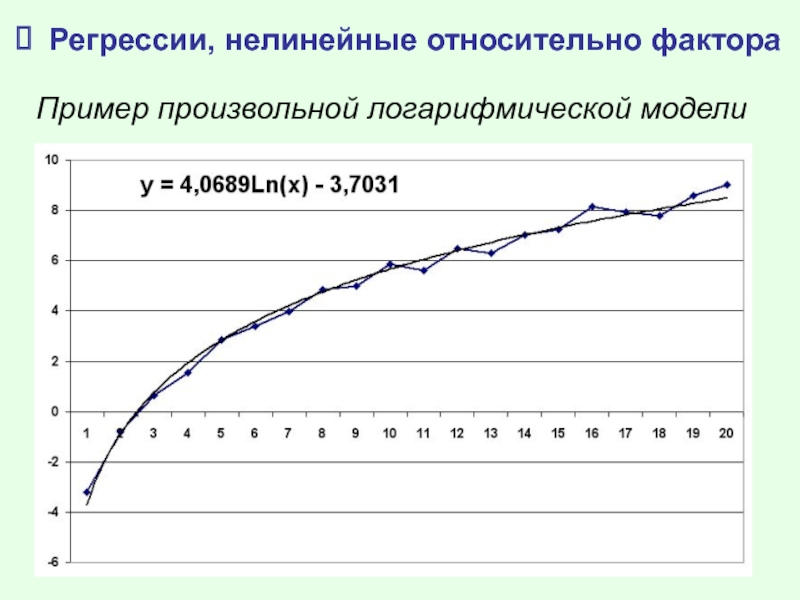
- 11. Регрессии, нелинейные относительно фактора Пример произвольной логарифмической модели
- 12. Регрессии, нелинейные относительно фактора Применение логарифмических моделей
- 13. Регрессии, нелинейные относительно параметров
- 14. Регрессии, нелинейные относительно параметров В степенной функции регрессии показатель b является коэффициентом эластичности*
- 15. Регрессии, нелинейные относительно параметров Степенная регрессия
- 16. 2. Оценка параметров нелинейной модели относительно фактора
- 17. Полиномиальная, гиперболическая и логарифмическая модели сводятся
- 18. Полиномиальная модель На практике используются полиномы не
- 19. Гиперболическая модель Преобразование: Получили линейную модель : Применяя МНК, получаем формулы для расчета параметров модели:
- 20. Логарифмическая модель Преобразование: Получили линейную модель : Применяя МНК, получаем формулы для расчета параметров модели:
- 21. 3. Оценка параметров нелинейной модели по параметрам
- 22. Некоторые нелинейные модели по параметрам можно привести к линейному виду путем линеаризации
- 23. Примеры нелинейных моделей и их линеаризация
- 24. Оценка параметров линеаризованных моделей МНК применяют
- 25. Оценка параметров линеаризованных моделей Решение задачи минимизации сводится к решению системы нормальных уравнений
- 26. Оценка параметров линеаризованных моделей Продолжение: преобразование системы нормальных уравнений
- 27. Оценка параметров линеаризованных моделей Продолжение: из
- 28. Известно, что коэффициент эластичности для любой парной
- 29. Упражнение 2. По совокупности 30 предприятий торговли
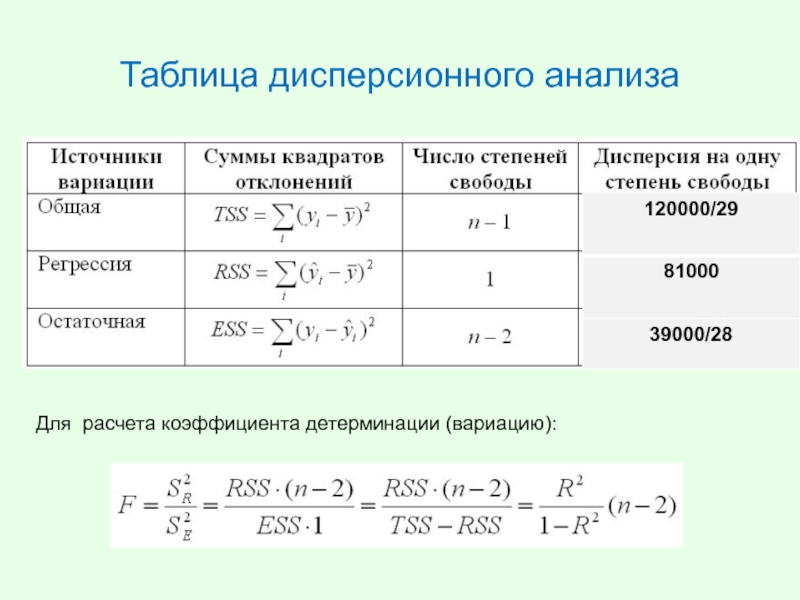
- 30. Таблица дисперсионного анализа Для расчета коэффициента детерминации (вариацию):
- 31. Литература: Елисеева И.И. Практикум по эконометрике: Учебное
План: Общие сведения о нелинейных парных регрессионных моделях, виды нелинейных регрессий Оценка параметров нелинейной модели относительно фактора Оценка параметров нелинейной модели по параметрам
Слайд 2План:
Общие сведения о нелинейных парных регрессионных моделях, виды нелинейных регрессий
Оценка параметров
нелинейной модели относительно фактора
Оценка параметров нелинейной модели по параметрам
Оценка параметров нелинейной модели по параметрам
Слайд 4Различают два класса нелинейных регрессий:
регрессии, нелинейные относительно фактора, но линейные по
параметрам
Регрессии, нелинейные по параметрам
Регрессии, нелинейные по параметрам
Слайд 7Регрессии, нелинейные относительно фактора
Применение полиномиальных моделей
Полиномом второй степени могут быть представлены
зависимости:
Заработная плата физического труда от возраста
Урожайность от количества внесенных удобрений
Прибыль от количества каналов, исполняющих заявки в системе массового обслуживания и т.д.
Заработная плата физического труда от возраста
Урожайность от количества внесенных удобрений
Прибыль от количества каналов, исполняющих заявки в системе массового обслуживания и т.д.
Слайд 8Регрессии, нелинейные относительно фактора
Применение гиперболических моделей
Классический пример: кривая Филлипса - графическое
отображение обратной зависимости между уровнем инфляции и уровнем безработицы.
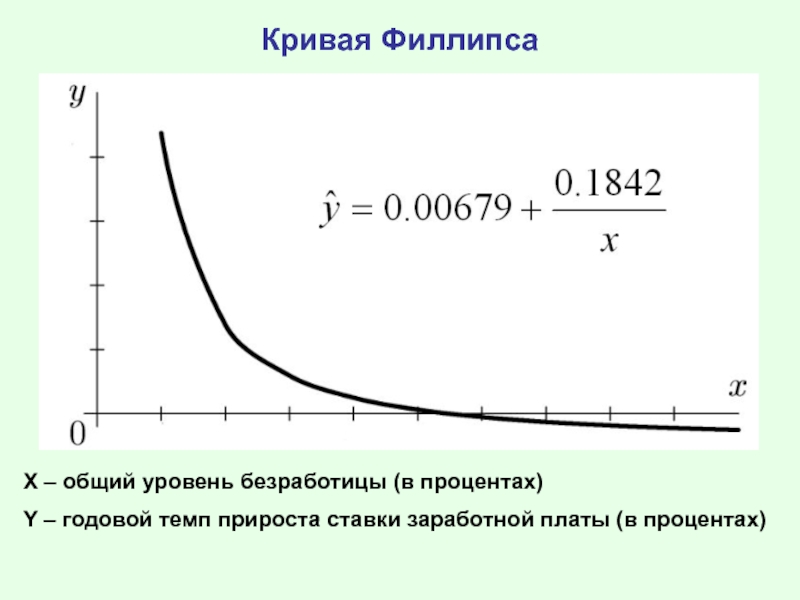
Слайд 9Кривая Филлипса
Х – общий уровень безработицы (в процентах)
Y – годовой темп
прироста ставки заработной платы (в процентах)
Слайд 10Кривая Филлипса
Олбан Уильям Филлипс (1914-1975) - австралийский экономист, работавший в Англии.
Кривую Филлипса получил в 1958 г. на основе эмпирических данных по Англии за 1861-1957 годы
Слайд 12Регрессии, нелинейные относительно фактора
Применение логарифмических моделей
Может быть использована для описания доли
расходов на товары длительного пользования (кривая Энгеля) в зависимости от общих сумм расходов
Эрнст Энгель (26.03.1821 - 08.12.1896) - немецкий экономист и статистик, занимал должность директора Прусского статистического бюро в Берлине
Слайд 14Регрессии, нелинейные относительно параметров
В степенной функции регрессии показатель b является коэффициентом
эластичности*
Слайд 15
Регрессии, нелинейные относительно параметров
Степенная регрессия нашла большое использование в производственных функциях,
в исследованиях спроса и потребления
Производственная функция валового внутреннего продукта США по данным 1960-1995 гг.
Y – валовой внутренний продукт США
К – капитал
L - труд
Слайд 17Полиномиальная, гиперболическая и логарифмическая модели
сводятся
к линейной форме
заменой переменных
Затем
используются известные соответствующие методы оценивания параметров и проверки гипотез
Слайд 18Полиномиальная модель
На практике используются полиномы не более третьего порядка
Введем новые переменные:
Получили
линейную модель множественной регрессии:
Слайд 19Гиперболическая модель
Преобразование:
Получили линейную модель :
Применяя МНК, получаем формулы для расчета параметров
модели:
Слайд 20Логарифмическая модель
Преобразование:
Получили линейную модель :
Применяя МНК, получаем формулы для расчета параметров
модели:
Слайд 22Некоторые нелинейные модели по параметрам можно
привести к линейному виду путем
линеаризации
Слайд 24Оценка параметров линеаризованных моделей
МНК применяют к преобразованному линеаризованному уравнению
Пример: степенная регрессия
Логарифмируем:
Цель:
Слайд 25Оценка параметров линеаризованных моделей
Решение задачи минимизации сводится к решению системы нормальных
уравнений
Слайд 26Оценка параметров линеаризованных моделей
Продолжение: преобразование системы нормальных уравнений
Слайд 27Оценка параметров линеаризованных моделей
Продолжение: из системы нормальных уравнений
выражаем параметры с
учетом замены
Готовые
формулы
Слайд 28Известно, что коэффициент эластичности для любой парной зависимости:
Тогда для степенной НПР:
Эластичность:
Упражнение
1. Доказать, что в степенной функции регрессии показатель b является коэффициентом эластичности
Решение:
Слайд 29Упражнение 2. По совокупности 30 предприятий торговли изучается зависимость между признаками:
х – цена на товар, тыс. руб.; у – прибыль торгового предприятия, млн. руб.
При оценке регрессионной модели были получены следующие промежуточные результаты:
а) Какой показатель корреляции можно определить по этим данным? Рассчитайте его
б) Постройте таблицу дисперсионного анализа для расчета значения F-критерия Фишера
в) Сравните фактическое значение F-критерия с табличным. Сделайте выводы.
Слайд 31Литература:
Елисеева И.И. Практикум по эконометрике: Учебное пособие. - М.: Финансы и
статистика, 2005 - 192 с.
Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов. М.: ЮНИТИ-ДАНА, 2005. – 311 с.
Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. – М.: ЮНИТИ, 1998. – 1005 с.
Эконометрика. Курс лекций. – Учебно-методическое пособие. Составители: Козинова А.Т., Отделкина А.А. – Н.Новгород, 2004. – 95 с.
Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов. М.: ЮНИТИ-ДАНА, 2005. – 311 с.
Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. – М.: ЮНИТИ, 1998. – 1005 с.
Эконометрика. Курс лекций. – Учебно-методическое пособие. Составители: Козинова А.Т., Отделкина А.А. – Н.Новгород, 2004. – 95 с.
