- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функция y=ах2+bx+c, ее свойства и график презентация
Содержание
- 1. Функция y=ах2+bx+c, ее свойства и график
- 2. a, b, c – числа (коэффициенты), Квадратный
- 3. Пример 1: Построить график функции y=-3x2-6x+1.
- 4. Теорема: Графиком квадратичной функции y=ax2+bx+c является парабола,
- 5. Теорема: Графиком квадратичной функции y=ax2+bx+c является парабола,
- 6. Пример 2: Не выполняя построения графика функции
- 7. Ветви параболы y=ax2+bx+c направлены вверх, если а>0, и вниз, если a
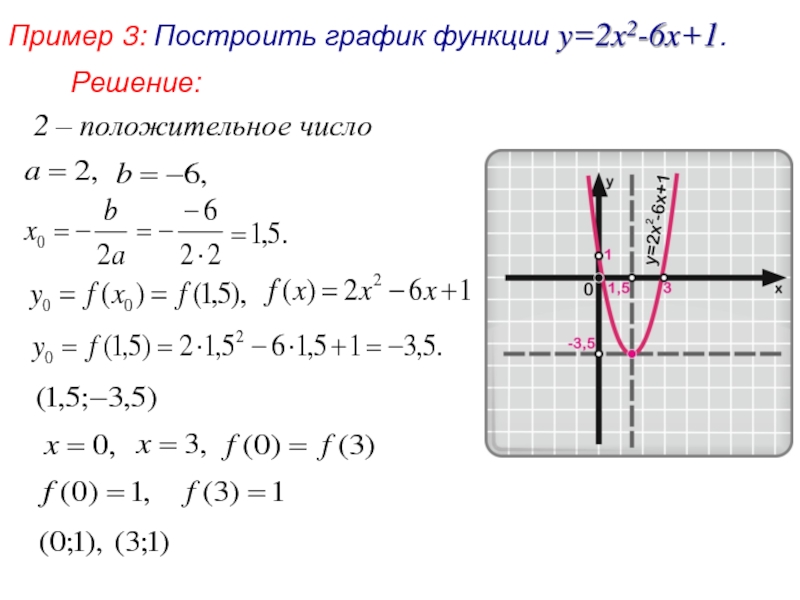
- 8. Пример 3: Построить график функции y=2x2-6x+1. 2 – положительное число Решение:
- 9. Алгоритм построения параболы y = аx2 +
- 10. Пример 4: Найти наименьшее и наибольшее значения
Слайд 1ФУНКЦИЯ y=ах2+bx+c,
ЕЕ СВОЙСТВА И ГРАФИК
Алгебра(1 час) 09 февраля
Задание:
Повторить
Решить в рабочей тетради
(поставить дату 09.02) следующие задания из задачника:
22.7, 22.8, 22.9, 22.10
Слайд 2a, b, c – числа (коэффициенты),
Квадратный трехчлен
ах2 – старший член квадратного
а – старший коэффициент квадратного трехчлена.
a = 3, b = 2, c = 0.
Функцию , где a, b, c – произвольные числа, причем , называют квадратичной функцией.
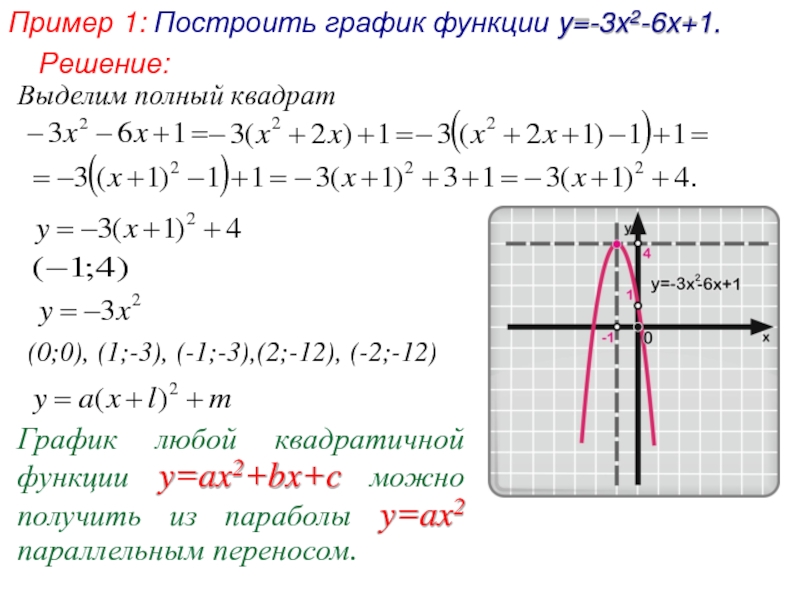
Слайд 3Пример 1: Построить график функции y=-3x2-6x+1.
(0;0), (1;-3), (-1;-3),(2;-12), (-2;-12)
Выделим полный
График любой квадратичной функции y=ax2+bx+c можно получить из параболы y=ax2 параллельным переносом.
Решение:
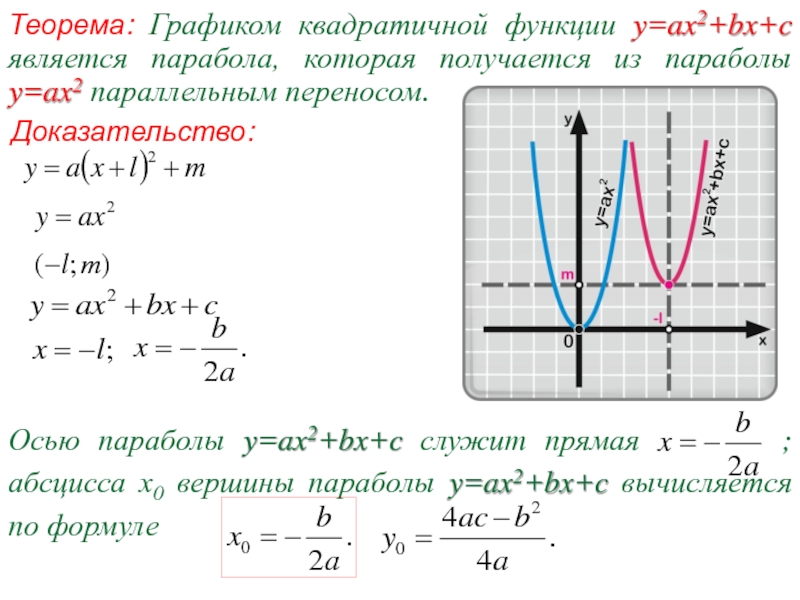
Слайд 4Теорема: Графиком квадратичной функции y=ax2+bx+c является парабола, которая получается из параболы
Доказательство:
Метод выделения полного квадрата
Слайд 5Теорема: Графиком квадратичной функции y=ax2+bx+c является парабола, которая получается из параболы
Доказательство:
Осью параболы y=ax2+bx+c служит прямая ; абсцисса х0 вершины параболы y=ax2+bx+c вычисляется по формуле
Слайд 6Пример 2: Не выполняя построения графика функции y=-3x2-6x+1, ответить на следующие
а) Какая прямая служит осью параболы?
б) Каковы координаты вершины параболы?
в) Куда (вверх или вниз) направлены ветви параболы?
а)
б)
в)
Решение:
Слайд 9Алгоритм построения параболы y = аx2 + bx + c :
1.
2. Отметить на оси х две точки, симметричные относительно оси параболы (чаще всего в качестве одной из таких точек берут точку х=0), найти значения функции в этих точках; построить на координатной плоскости соответствующие точки.
3. Через полученные три точки провести параболу
(в случае необходимости берут еще пару точек, симметричных относительно оси параболы, и строят параболу по пяти точкам).
Слайд 10Пример 4: Найти наименьшее и наибольшее значения функции y=-2x2+8x-5 на отрезке
I этап.
1).
2).
(2;3), (0;-5), (4;-5)
3).
II этап.
унаим=-5 (при х=0)
унаиб=3 (при х=2)
Решение:






![Пример 4: Найти наименьшее и наибольшее значения функции y=-2x2+8x-5 на отрезке [0;3].I этап.1).2).(2;3), (0;-5), (4;-5)3).II](/img/tmb/1/74056/269e27c427f7b568bb3e2a9b02c8b5d4-800x.jpg)





