- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функция у=х в степени n , график и свойства презентация
Содержание
- 1. Функция у=х в степени n , график и свойства
- 2. Линейная функция (прямая пропорциональность), график - прямая,
- 3. Квадратичная функция, график – парабола, вершина которой
- 4. Тема: «Функции у = хn (n Є N), их свойства и графики».
- 5. Определение Функцию у = хn ,
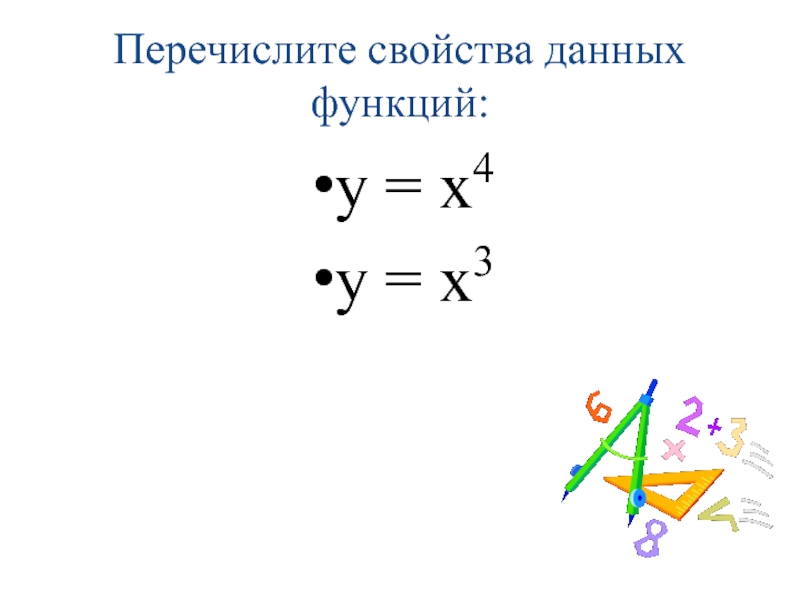
- 6. Перечислите свойства данных функций: у = х4 у = х3
- 7. у = х4 Составим таблицу значений для этой функции:
- 8. у = х4
- 9. Свойства функции у = х4: D(у) =
- 10. Функция у = х2n Речь идет о
- 11. у = х3 Составим таблицу значений для этой функции:
- 12. у = х3
- 13. Свойства функции у = х3 D(у) =
- 14. Функция у = х2n+1 Речь идет о
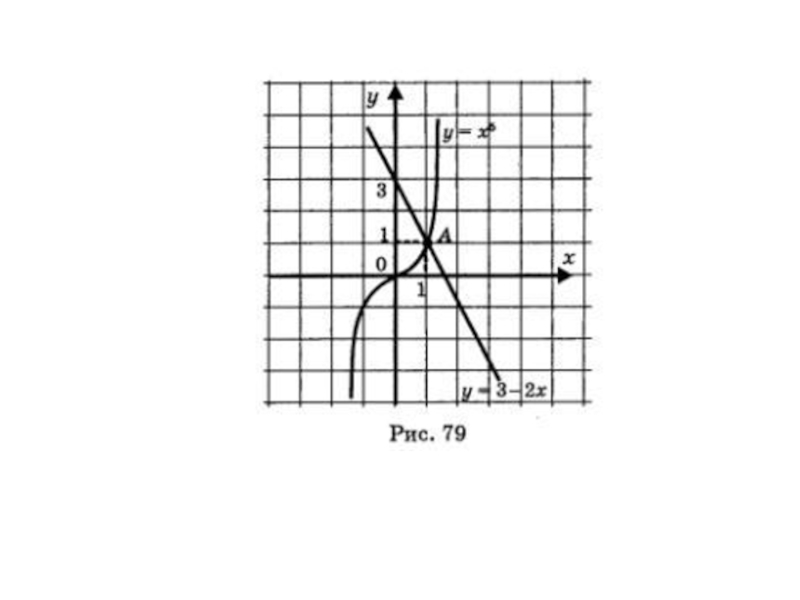
- 15. Пример 1. Решить уравнение: х5 = 3 - 2х.
Слайд 1Что называется функцией?
Функция – это зависимость одной переменной величины от другой.
2) Что
График функции - множество точек, у которых значению х есть значение у.
3) Какие свойства функции мы уже исследовали?
4) Что является графиком функции у = х? Перечислите свойства этой функции.
5) Что является графиком функции у = х2? Перечислите свойства этой функции.
Что является графиком функции у = х723? Перечислите свойства этой функции.
А хотели бы вы это узнать? Тогда помогите мне определить тему сегодняшнего урока, а для этого продолжите ряд функций:
у = х, у = х2,………….
8) Входит ли в этот ряд функция у = х723?
9) Так какова же тема нашего урока?
10) Для каких значений n мы будем рассматривать эти функции?
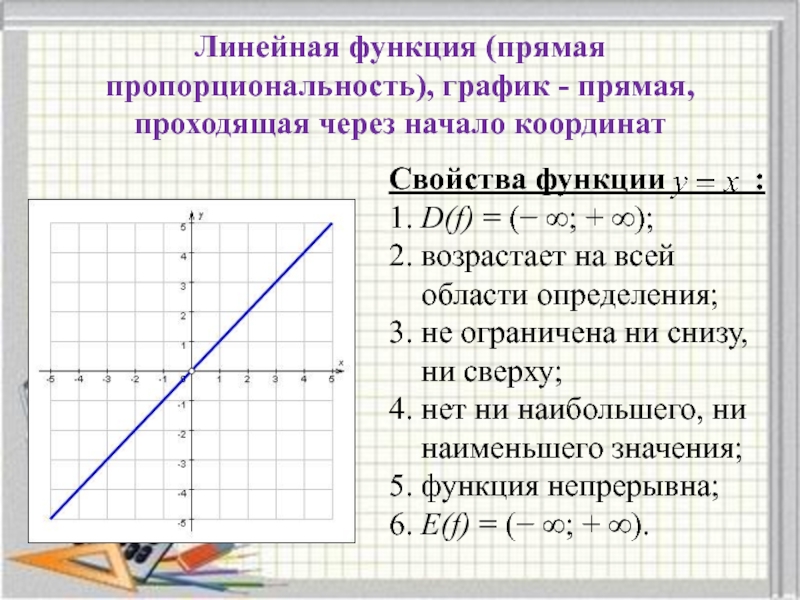
Слайд 2Линейная функция (прямая пропорциональность), график - прямая, проходящая через начало координат
Свойства
1. D(f) = (− ∞; + ∞);
2. возрастает на всей
области определения;
3. не ограничена ни снизу,
ни сверху;
4. нет ни наибольшего, ни
наименьшего значения;
5. функция непрерывна;
6. Е(f) = (− ∞; + ∞).
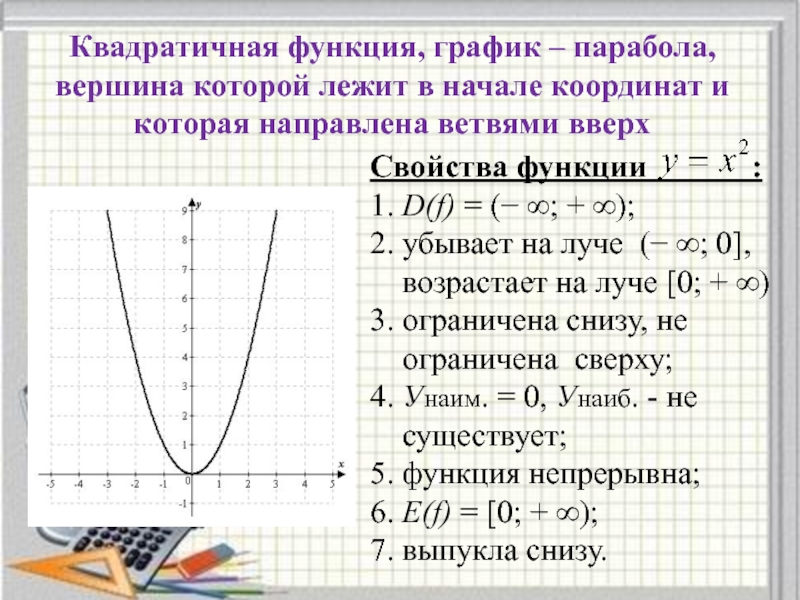
Слайд 3Квадратичная функция, график – парабола, вершина которой лежит в начале координат
Свойства функции :
1. D(f) = (− ∞; + ∞);
2. убывает на луче (− ∞; 0],
возрастает на луче [0; + ∞)
3. ограничена снизу, не
ограничена сверху;
4. Унаим. = 0, Унаиб. - не
существует;
5. функция непрерывна;
6. Е(f) = [0; + ∞);
7. выпукла снизу.
Слайд 5Определение
Функцию у = хn , где n = 1, 2, 3,
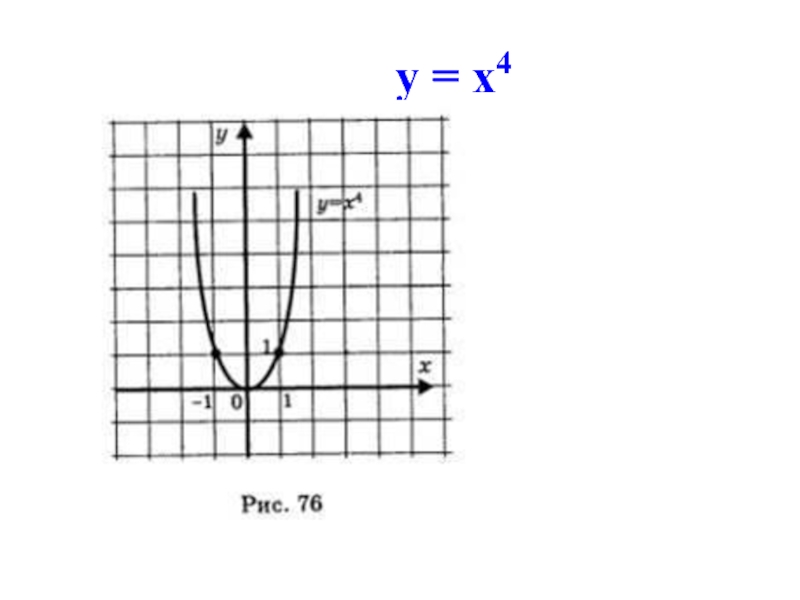
Слайд 9Свойства функции у = х4:
D(у) = (-∞,+∞);
четная функция;
убывает(-∞, 0], возрастает
Ограничена снизу, не ограничена сверху;
У наим.= 0, У наиб. нет;
непрерывна;
Е(у) = [0, +∞);
выпукла вниз.
Слайд 10Функция у = х2n
Речь идет о функциях у = х6, у
График любой такой функции похож на график функции у = х4, только его ветви более круто направлены вверх.
Отметим еще, что кривая у = х2n касается оси х в точке (0; 0), т.е. одна ветвь кривой плавно переходит в другую, как бы прижимаясь к оси х.
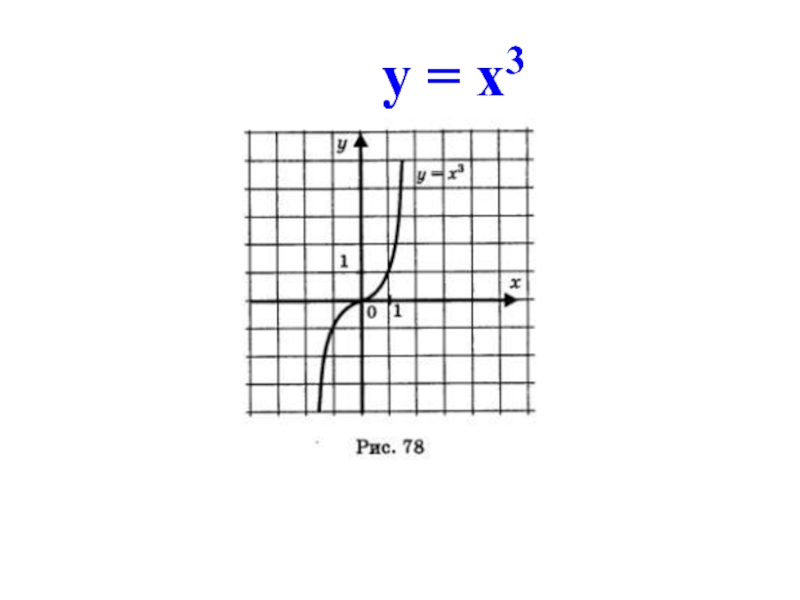
Слайд 13Свойства функции у = х3
D(у) = (-∞,+∞);
нечетная функция;
возрастает;
не ограничена ни
нет ни наименьшего, ни наибольшего значений;
непрерывна;
Е(у) = (-∞, +∞);
выпукла вверх при х < 0, выпукла вниз при х > 0.
Слайд 14Функция у = х2n+1
Речь идет о функциях у = х3, у
График любой такой функции похож на график у = х3 функции только чем больше показатель, тем более круто направлены вверх (и соответственно вниз) ветви графика.
Отметим еще, что кривая у =х2n+1 касается оси х в точке (0; 0).




![Свойства функции у = х4:D(у) = (-∞,+∞);четная функция; убывает(-∞, 0], возрастает [0; +∞) ;Ограничена снизу,](/img/tmb/5/482437/793b96ca35fb7ae0e72ac0335d084a9e-800x.jpg)