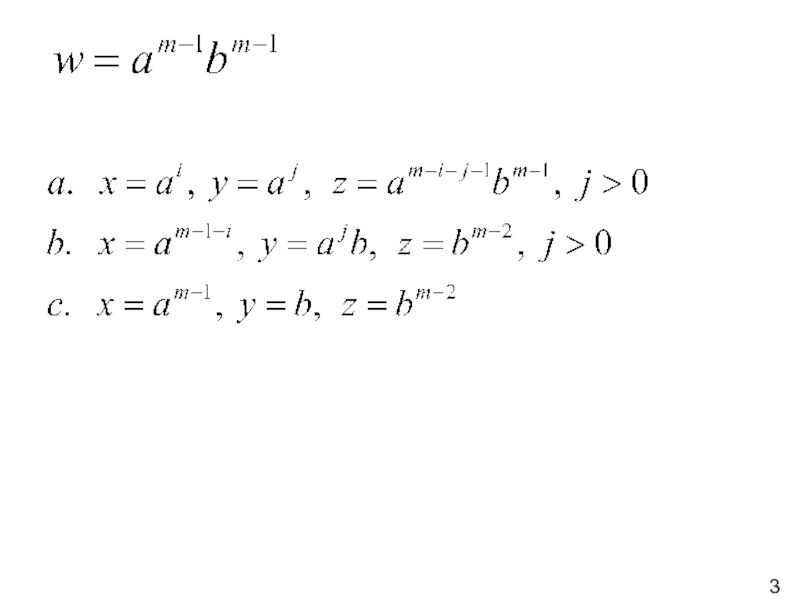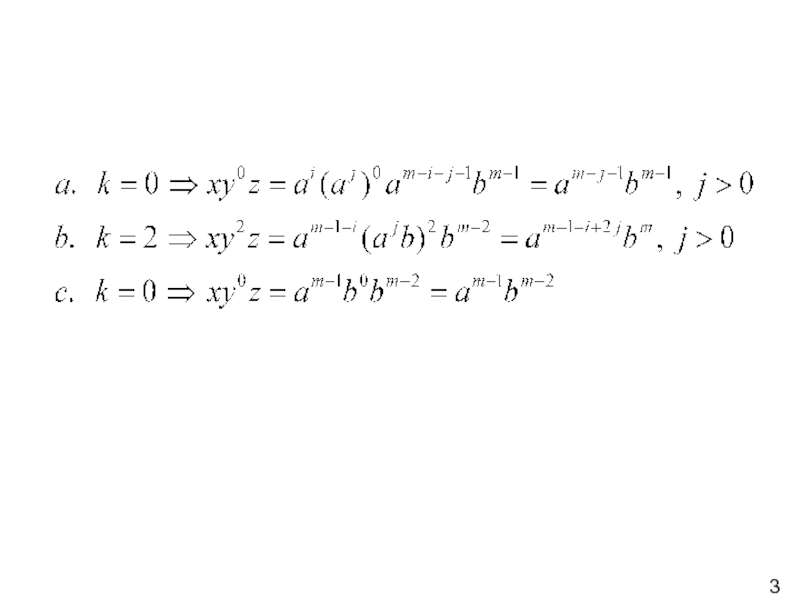- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Formālas valodas. Neregulāras valodas презентация
Содержание
- 1. Formālas valodas. Neregulāras valodas
- 2. Saturs Ievads Baložu ligzdas princips (Dirihlē princips) Pumpējošā lemma
- 3. Regulāras valodas Neregulāras valodas
- 4. Kā mēs varam pierādīt, ka valoda L
- 5. Baložu ligzdas princips
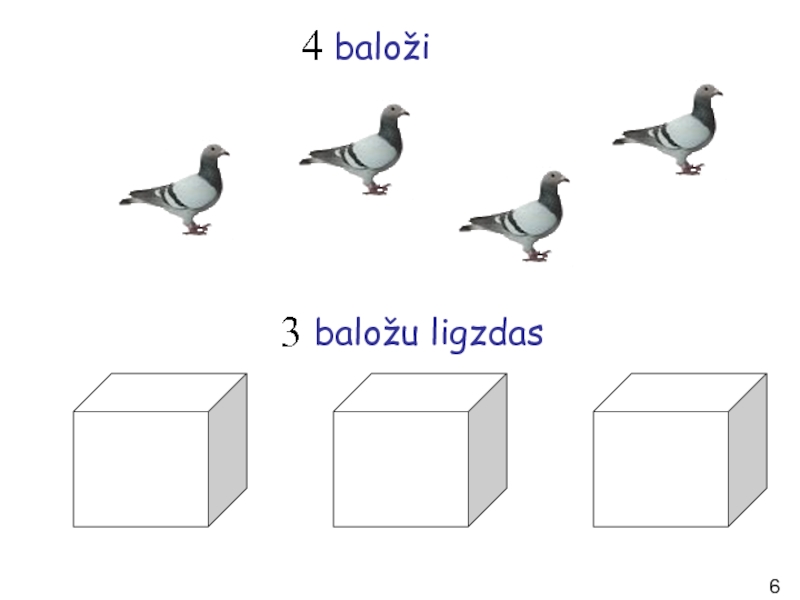
- 6. baloži baložu ligzdas
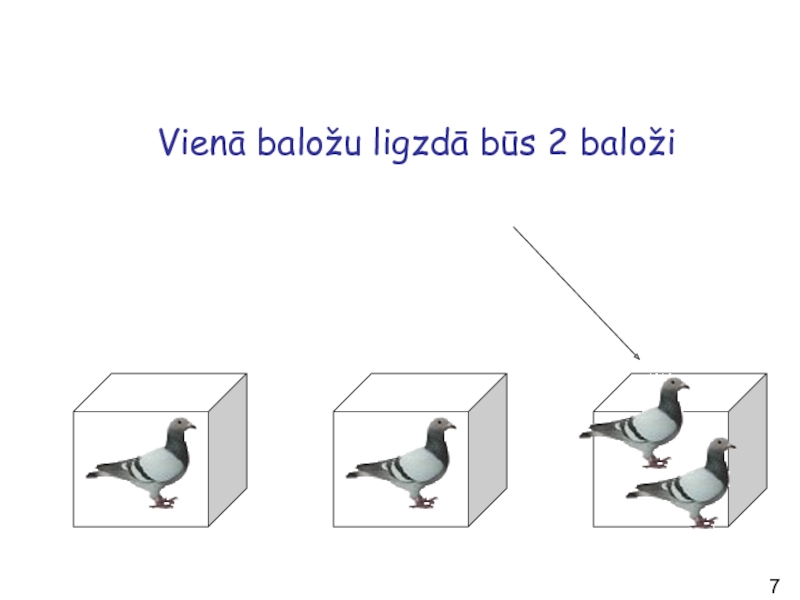
- 7. Vienā baložu ligzdā būs 2 baloži
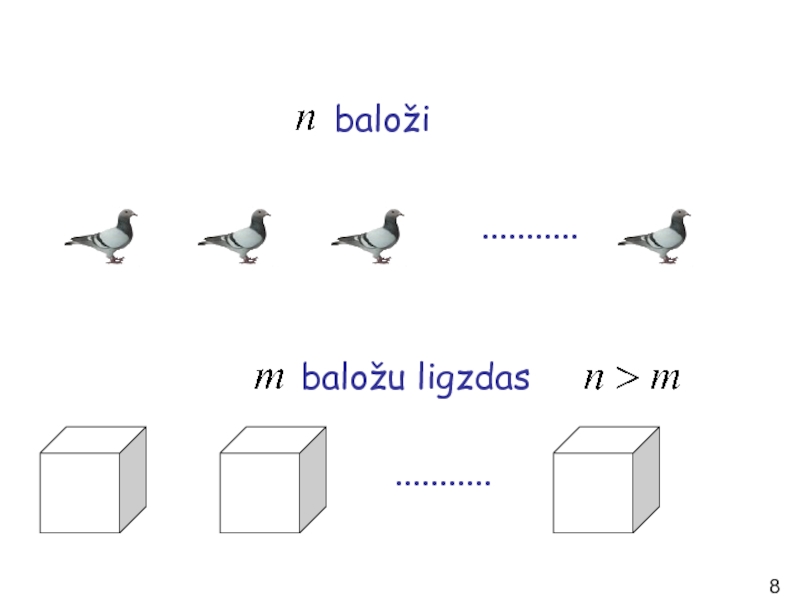
- 8. ........... ........... baloži baložu ligzdas
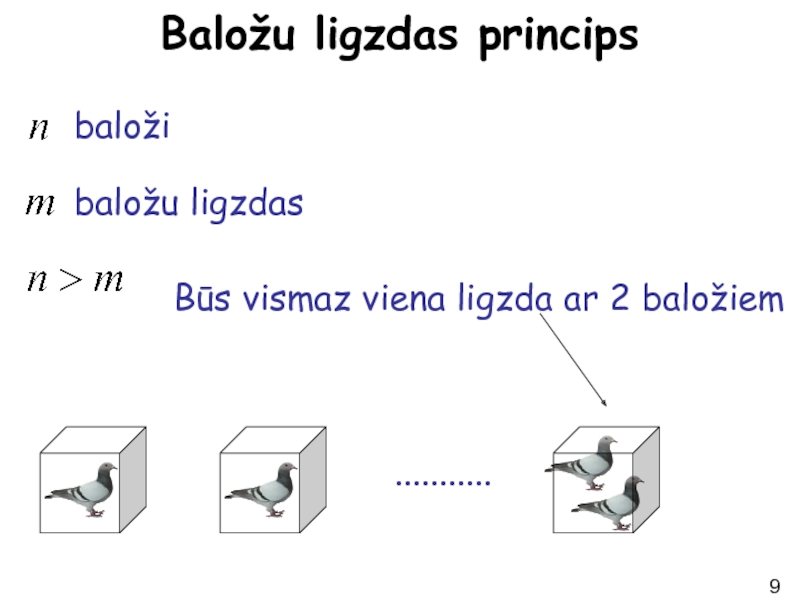
- 9. Baložu ligzdas princips
- 10. Baložu ligzdas princips un DFA
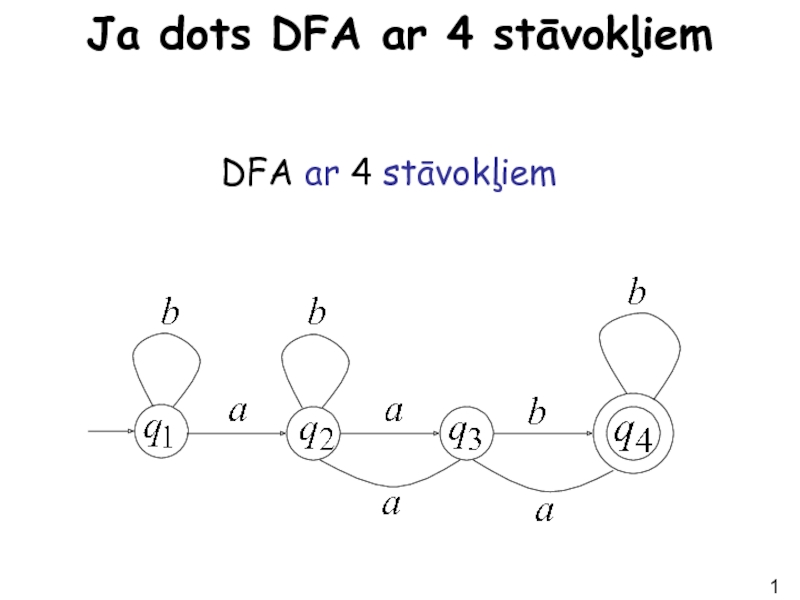
- 11. Ja dots DFA ar 4 stāvokļiem
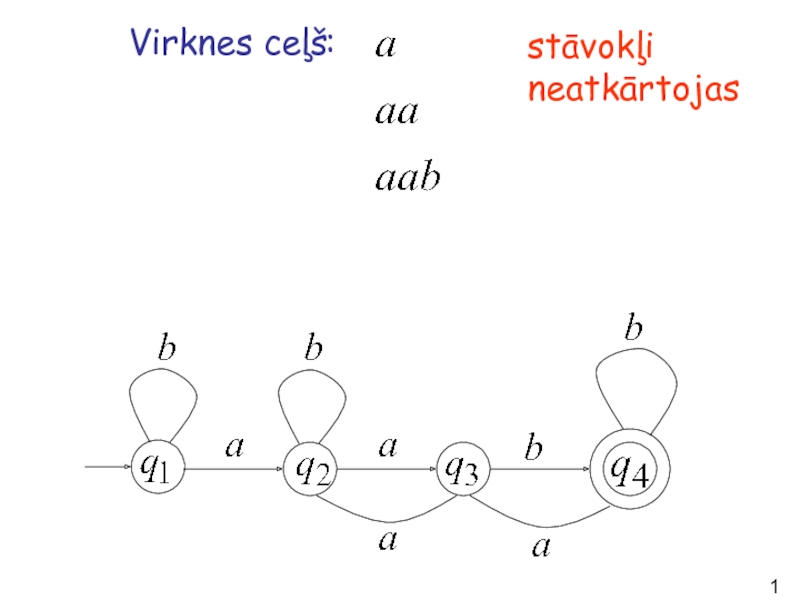
- 12. Virknes ceļš: stāvokļi neatkārtojas
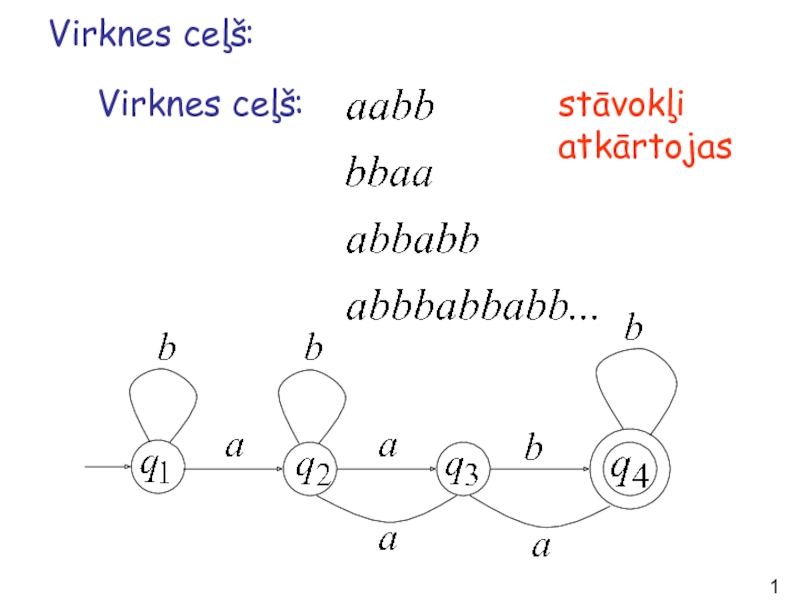
- 13. Virknes ceļš:
- 14. Ja virkne w, kuras garums
- 15. Jebkuram DFA: Virkne w, kuras garums
- 16. Citiem vārdiem virknei :
- 17. Pumpējošā lemma
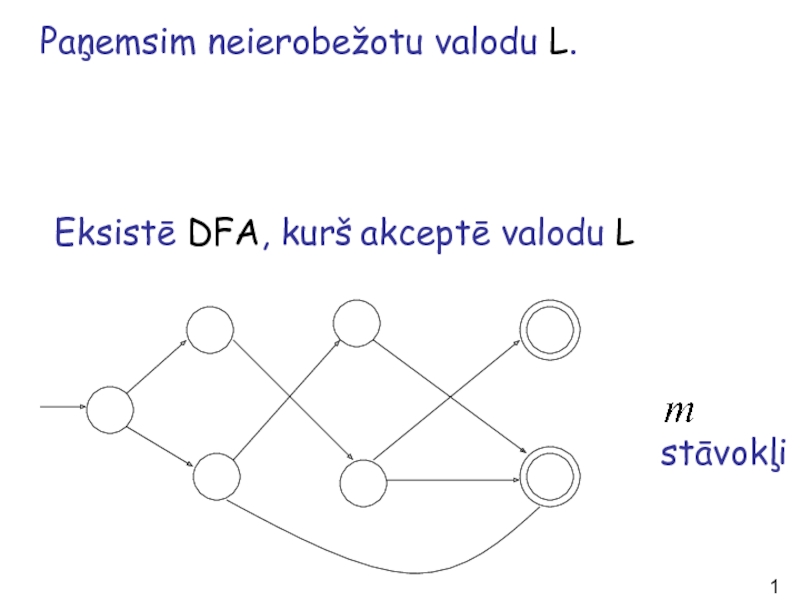
- 18. Paņemsim neierobežotu valodu L. Eksistē DFA, kurš
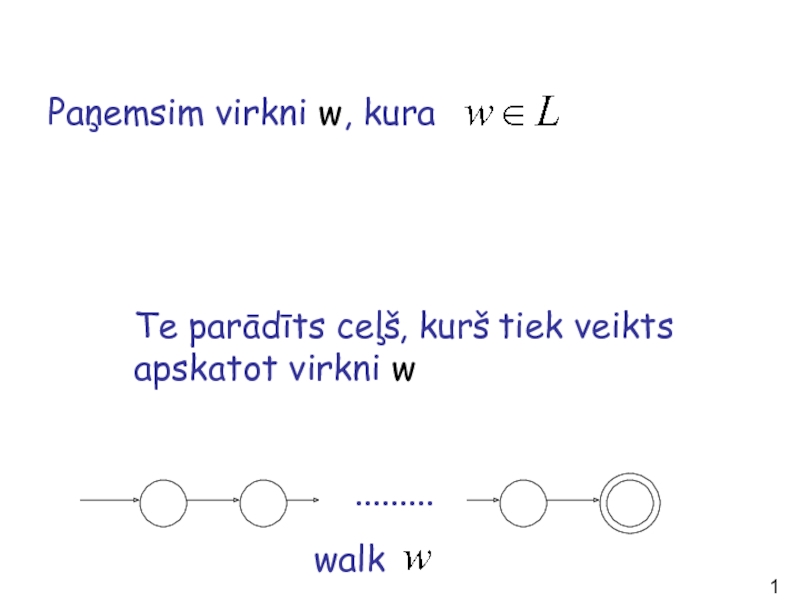
- 19. Paņemsim virkni w, kura Te parādīts ceļš,
- 20. Ja virkne w, kuras garums (DFA stāvokļu
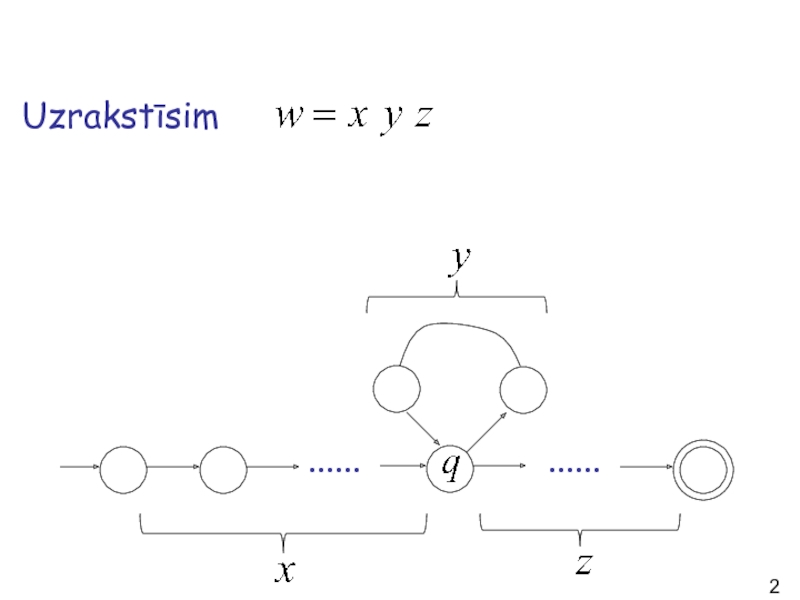
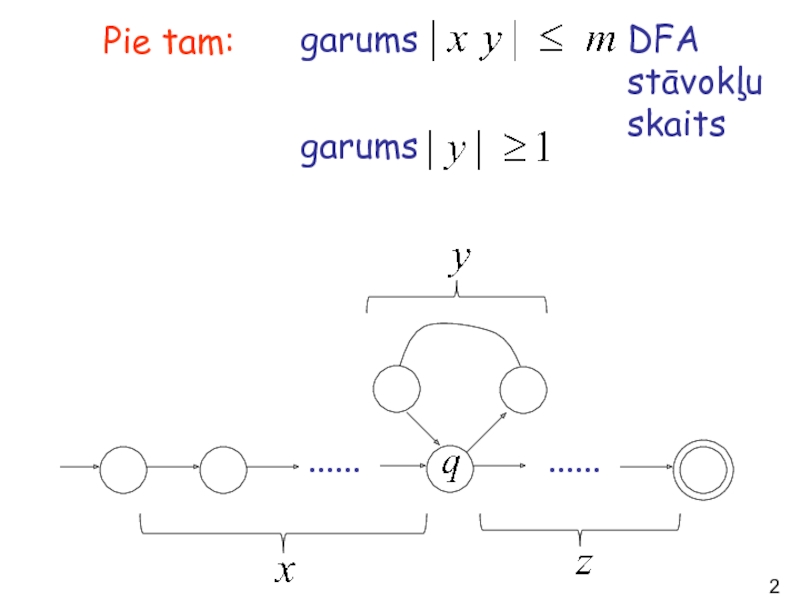
- 22. Uzrakstīsim ...... ......
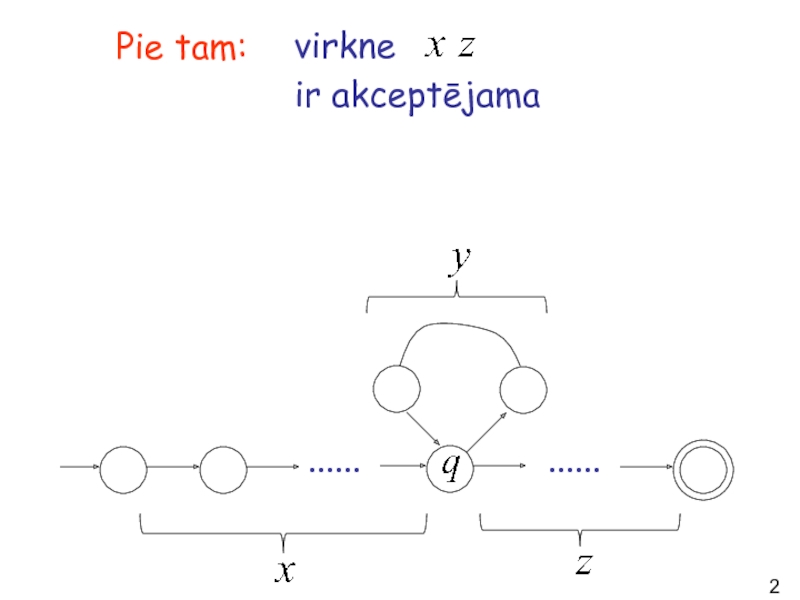
- 24. virkne ir
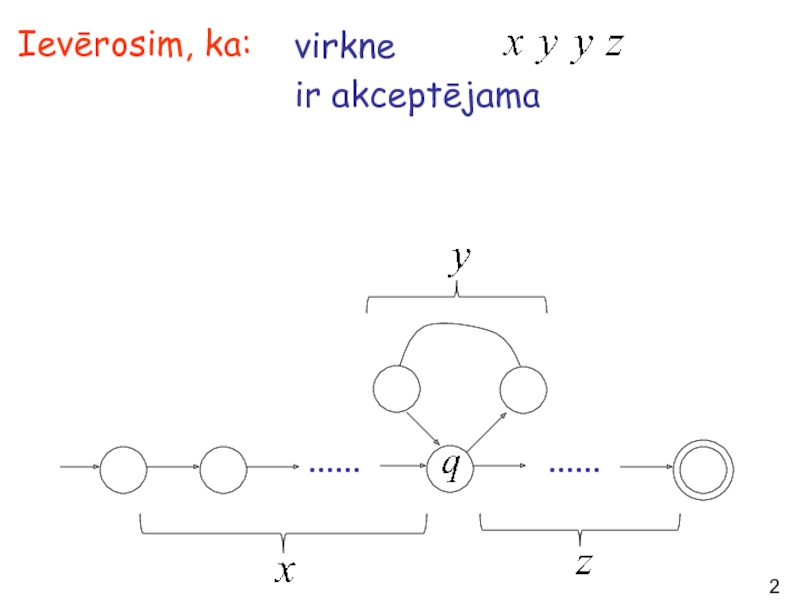
- 25. virkne ir
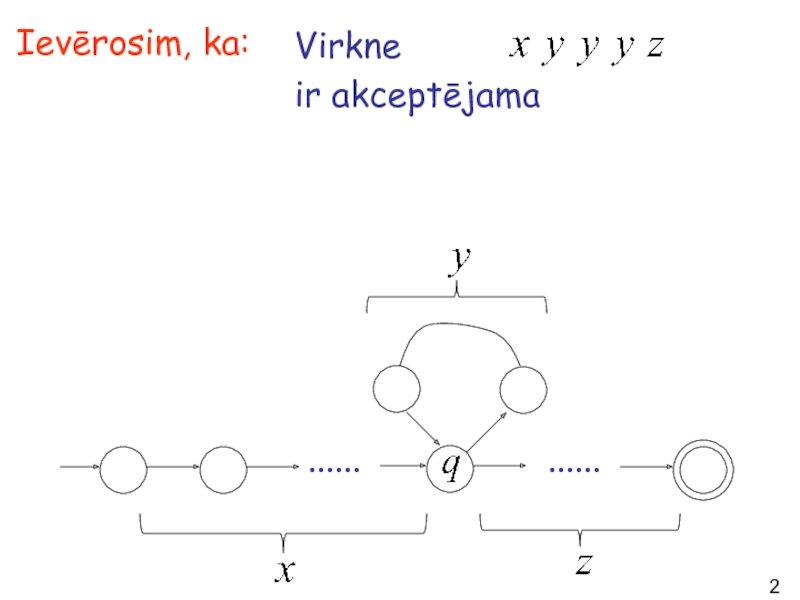
- 26. Virkne ir
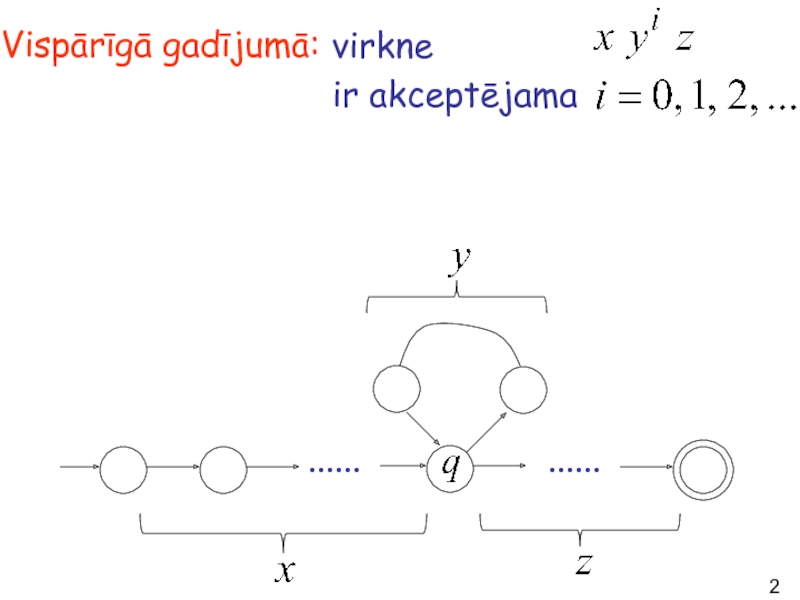
- 27. virkne ir
- 29. Citiem vārdiem, esam aprakstījuši: Pumpējošo lemmu !!!
- 30. Pumpējošā lemma Ņemot neierobežotu regulāru valodu
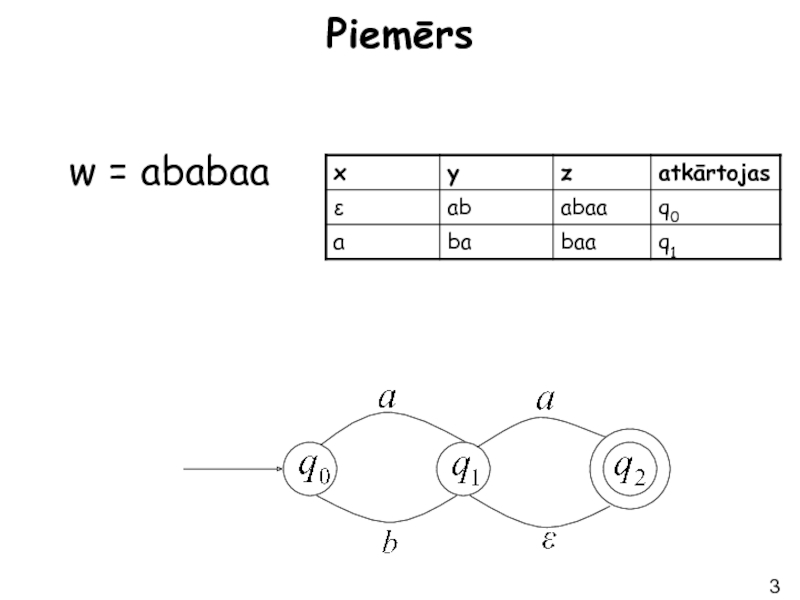
- 31. Piemērs w = ababaa
- 32. Pumpējošās lemmas izmantošana
- 33. Teorēma: Valoda nav regulāra Pierādījums: Izmanto Pumpējošo lemmu
- 34. Pieņemsim pretējo, ka L ir regulāra valoda
- 35. Pumpējošā lemmā m ir vesels skaitlis Izvēlēsimies virkni w, tādu, ka garums Pieņemsim
- 36. izriet, ka No Pumpējošās lemmas Rakstām: tādējādi:
- 37. No Pumpējošās lemmas Pretruna!!!
- 40. Mūsu pieņēmums, ka valoda L ir regulāra ir nepareizs. Slēdziens: Ir neregulāra valoda Tādēļ:
- 41. Regulāras valodas Neregulāras valodas
- 42. Uzdevumi Pierādīt, ka valodas ir neregulāras:
- 43. Pieņemsim pretējo, ka šī valoda ir regulāra.
- 44. Pieņemsim pretējo, ka šī valoda ir regulāra.
- 45. Pieņemsim pretējo, ka šī valoda ir regulāra.
Слайд 4Kā mēs varam pierādīt, ka valoda L nav regulāra?
Jāpierāda, ka neeksistē
Problēma: to nav tik vienkārši pierādīt.
Risinājums: Pumpējošā lemma !!!
Слайд 14
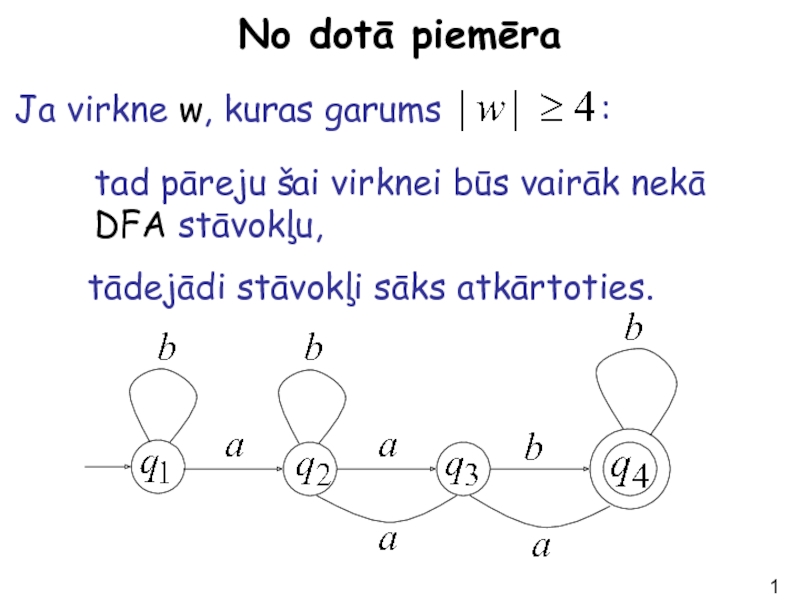
Ja virkne w, kuras garums
tādejādi stāvokļi sāks atkārtoties.
tad pāreju šai virknei būs vairāk nekā DFA stāvokļu,
No dotā piemēra
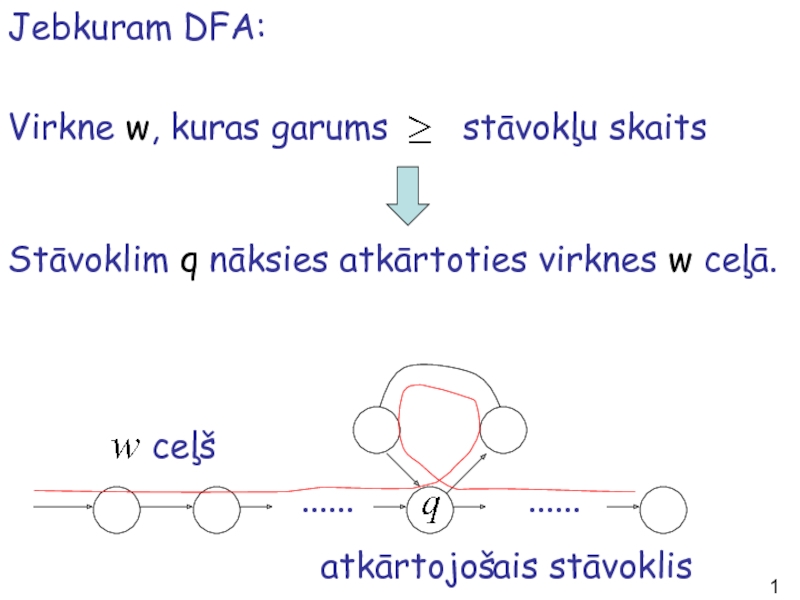
Слайд 15Jebkuram DFA:
Virkne w, kuras garums stāvokļu skaits
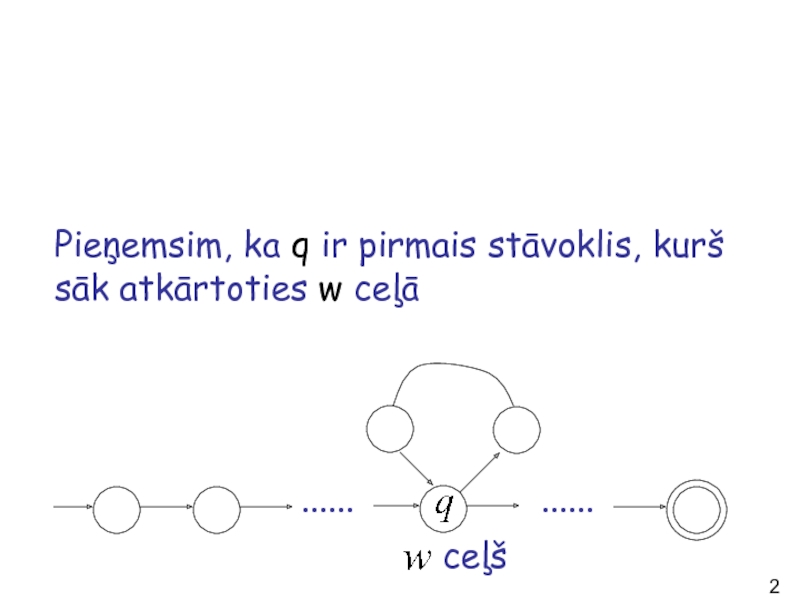
Stāvoklim q nāksies atkārtoties virknes w ceļā.
......
......
ceļš
atkārtojošais stāvoklis
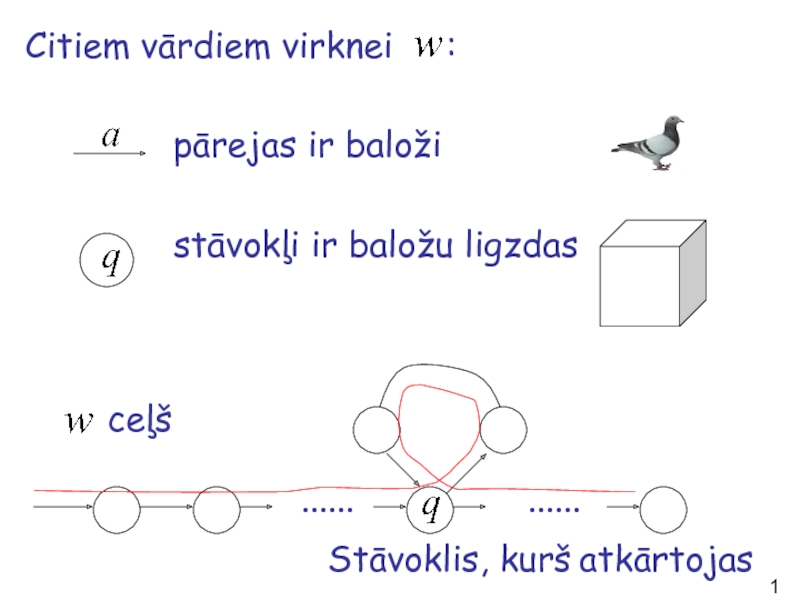
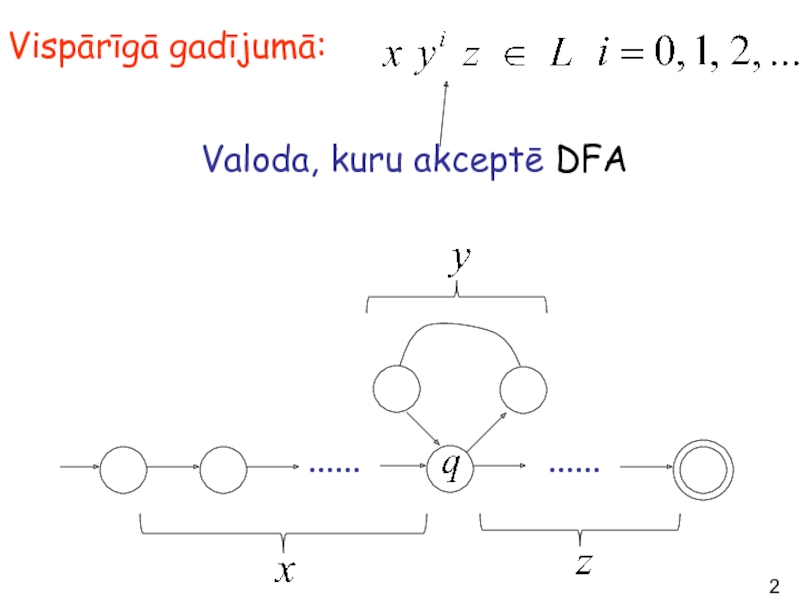
Слайд 16Citiem vārdiem virknei :
stāvokļi ir baložu ligzdas
......
......
ceļš
Stāvoklis, kurš atkārtojas
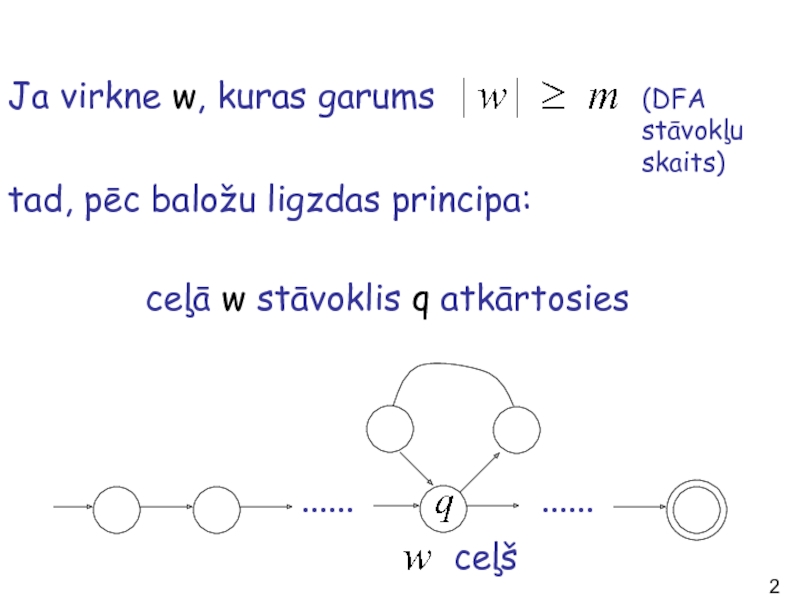
Слайд 20Ja virkne w, kuras garums
(DFA stāvokļu skaits)
tad, pēc baložu ligzdas principa:
ceļā w stāvoklis q atkārtosies
......
......
ceļš
Слайд 30Pumpējošā lemma
Ņemot neierobežotu regulāru valodu L
eksistē konstante m,
jebkurai virknei ar garumu
mēs varam rakstīt
kur un
tā ka:
Слайд 34Pieņemsim pretējo, ka
L ir regulāra valoda
Tā kā L ir neierobežota
mēs varam
Слайд 43Pieņemsim pretējo, ka šī valoda ir regulāra.
Tad ir spēkā Pumpējošā lemma
Izvēlēsimies:
Pieņemsim pretējo, ka šī valoda ir regulāra.
Tad ir spēkā Pumpējošā lemma – eksistē fiksēta konstante m, kas apmierina Pumpējošās lemmas nosacījumus.
Izvēlēsimies:
Слайд 44Pieņemsim pretējo, ka šī valoda ir regulāra.
Tad ir spēkā Pumpējošā lemma
Izvēlēsimies:
Pieņemsim pretējo, ka šī valoda ir regulāra.
Tad ir spēkā Pumpējošā lemma – eksistē fiksēta konstante m, kas apmierina Pumpējošās lemmas nosacījumus.
Izvēlēsimies:
K=0
Слайд 45Pieņemsim pretējo, ka šī valoda ir regulāra.
Tad ir spēkā Pumpējošā lemma
Izvēlēsimies:
Pieņemsim pretējo, ka šī valoda ir regulāra.
Tad ir spēkā Pumpējošā lemma – eksistē fiksēta konstante m, kas apmierina Pumpējošās lemmas nosacījumus.
Izvēlēsimies:
K=2