- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Факторный анализ презентация
Содержание
- 1. Факторный анализ
- 2. Факторный анализ Факторный анализ – как религия:
- 3. Основная идея Метод главных компонент объясняет наибольшую
- 4. Основная идея Факторный анализ объясняет отношения между
- 5. Основная идея Оба метода основываются на корреляциях
- 6. Основная идея Главными целями факторного анализа являются:
- 7. Метод главных компонент – это метод, который
- 8. Метод главных компонент ПРИМЕР: у студентов измерили
- 9. Метод главных компонент Если переменных в исследовании
- 10. Метод главных компонент Для этого и служит
- 11. Метод главных компонент y1=a11x1+a12x2+…+a1pxp y2=a21x1+a22x2+…+a2pxp … (1) yp=ap1x1+ap2x2+…+appxp
- 12. Метод главных компонент Переменные y1, y2, …,
- 13. Метод главных компонент Процедура извлечения факторов называется
- 14. Метод главных компонент Коэффициенты aij, определяющие новую
- 15. Метод главных компонент Часто полезно представить коэффициенты
- 16. Метод главных компонент Коэффициенты aij называются факторными нагрузками.
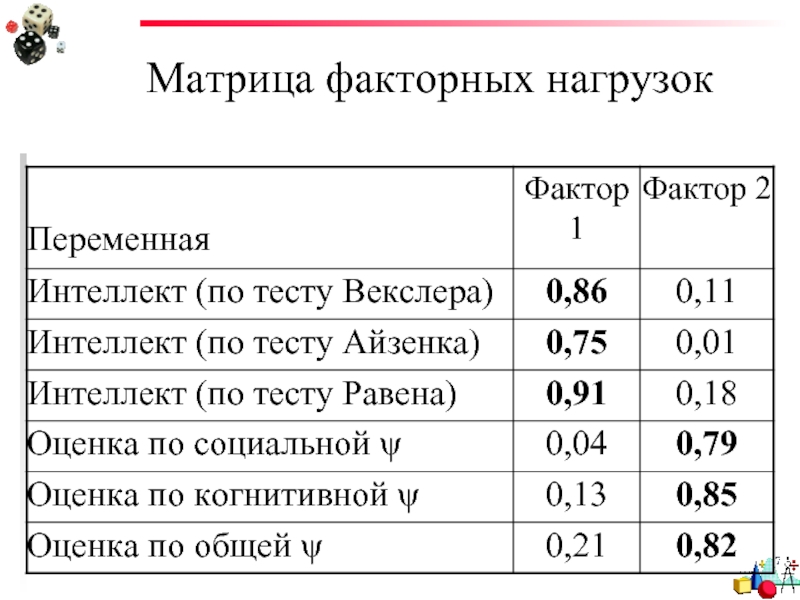
- 17. Матрица факторных нагрузок
- 18. Факторный анализ Основное отличие между факторным анализом
- 19. Факторный анализ Модель факторного анализа предполагает, что
- 20. Факторный анализ Дисперсия исходных переменных здесь объясняется
- 21. Факторный анализ x1=λ11f1+ λ 12f2+…+ λ1kfk+u1 x2=
- 22. Факторный анализ Случайная погрешность ui называется характерностью
- 23. Факторный анализ Общность (Communality) переменной xi -
- 24. Факторный анализ Если латентные факторы не коррелируют,
- 25. Факторный анализ Соответствие факторной модели полученным данным
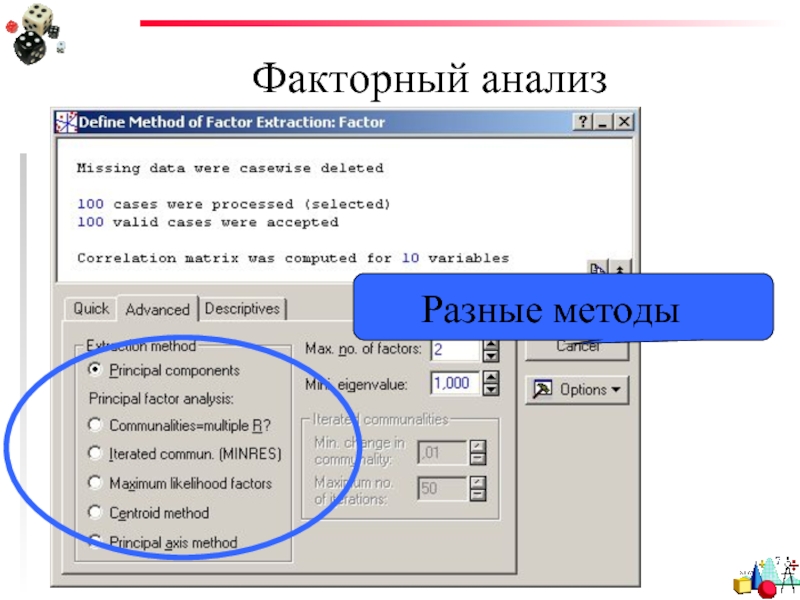
- 26. Факторный анализ В программе STATISTICA реализовано пять методов факторного анализа:
- 27. Факторный анализ Commonalities=multiple R-square. Если выбран
- 28. Факторный анализ Iterated commonalities (MINRES). Этот
- 29. Факторный анализ Maximum likelihood factors метод
- 30. Факторный анализ Centroid method – центроидный
- 31. Факторный анализ Principal axis method В
- 32. Факторный анализ Факторный анализ Statistics ⇒ Multivariate Exploratory Techniques ⇒ Factor Analysis
- 33. Факторный анализ Разные методы
- 34. Факторный анализ ☹ В SPSS реализованы некоторые перечисленные и некоторые другие методы
- 35. Факторный анализ ☺ Но! Факторные отображения одной
- 36. Факторный анализ Результаты, полученные с помощью метода
- 37. Сколько факторов? Для применения процедуры выбора следует
- 38. Сколько факторов?
- 39. Сколько факторов? 1) Процент объясненной
- 40. Сколько факторов?
- 41. Сколько факторов? 2) Критерий Кайзера
- 42. Сколько факторов?
- 43. Сколько факторов? 3) Критерий каменистой
- 44. Сколько факторов?
- 45. Сколько факторов? 4) На
- 46. Вращение матрицы факторных нагрузок
- 47. Вращение матрицы факторных нагрузок
- 48. Вращение матрицы факторных нагрузок
- 49. Вращение матрицы факторных нагрузок
- 50. Вращение матрицы факторных нагрузок
- 51. Вращение матрицы факторных нагрузок
- 52. Алгоритм факторного анализа Заносим данные в программу.
- 53. Алгоритм факторного анализа Выбираем количество факторов. Строим
- 54. Алгоритм факторного анализа Если ничего не получается,
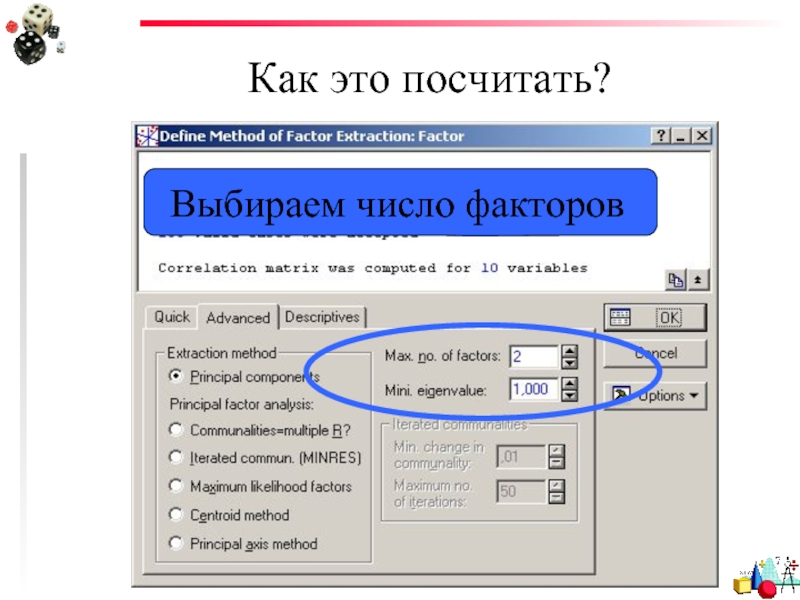
- 55. Как это посчитать? Выбираем число факторов
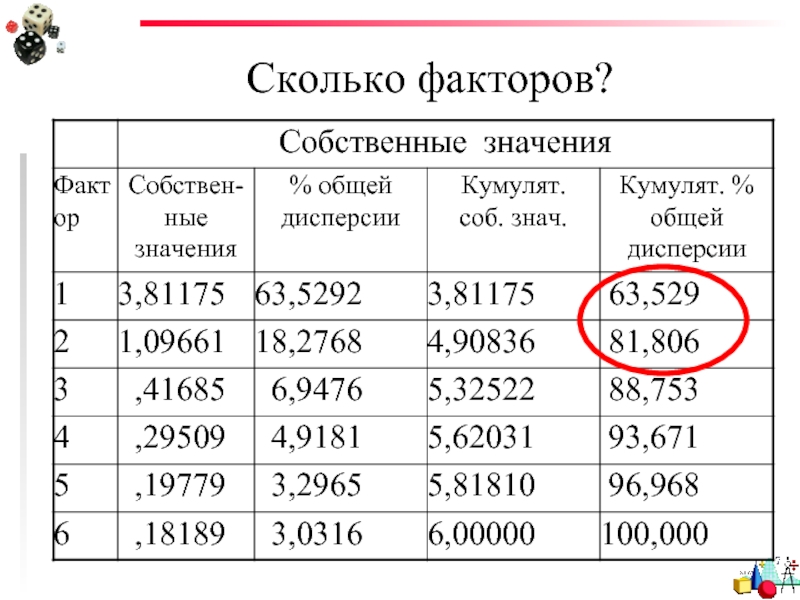
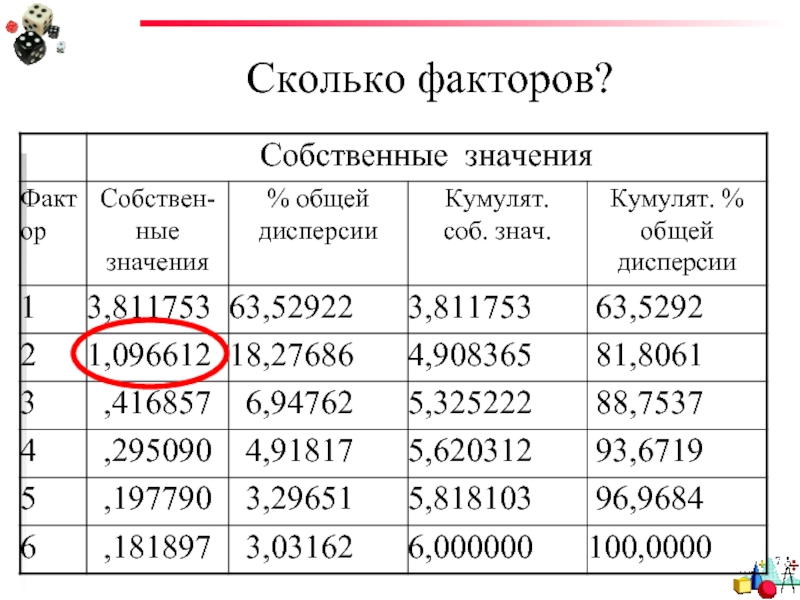
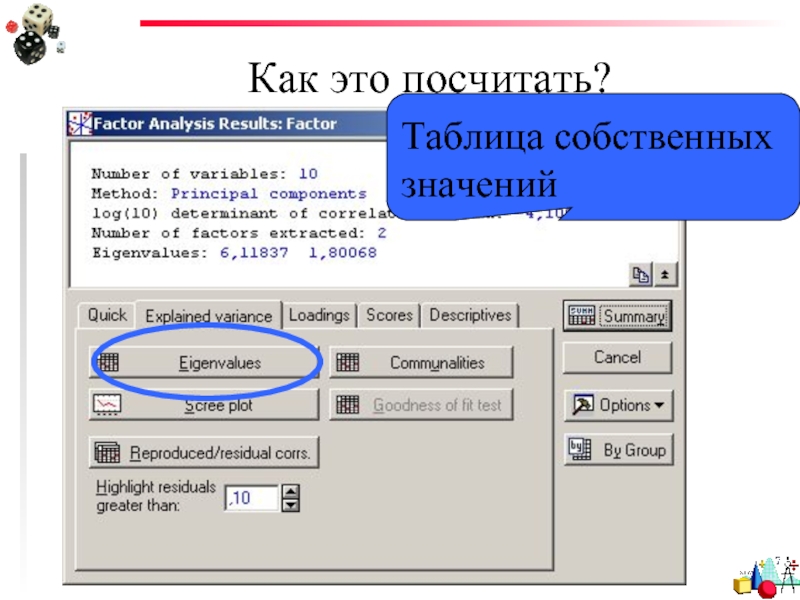
- 56. Как это посчитать? Таблица собственных значений
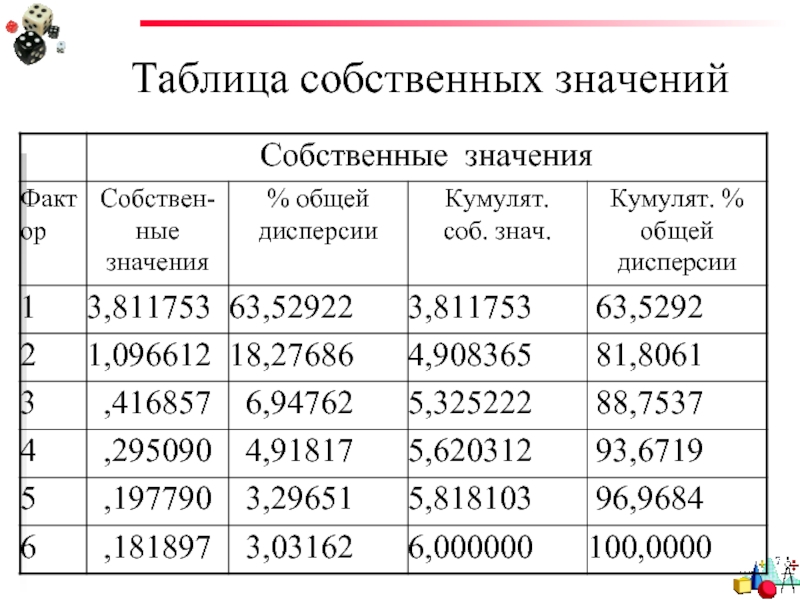
- 57. Таблица собственных значений
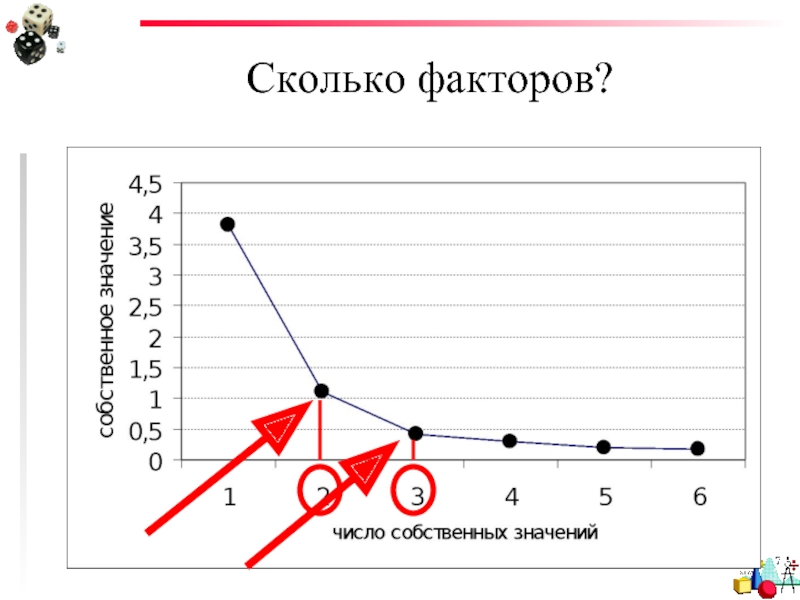
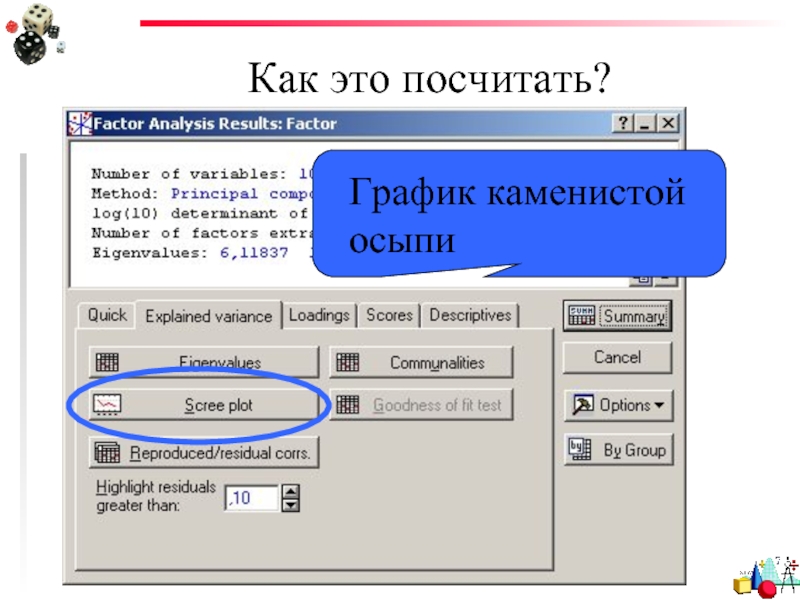
- 58. Как это посчитать? График каменистой осыпи
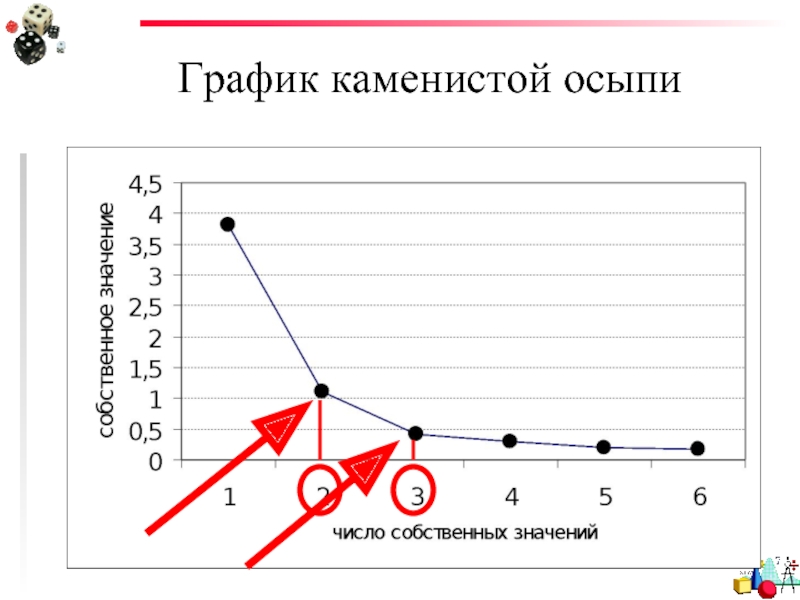
- 59. График каменистой осыпи
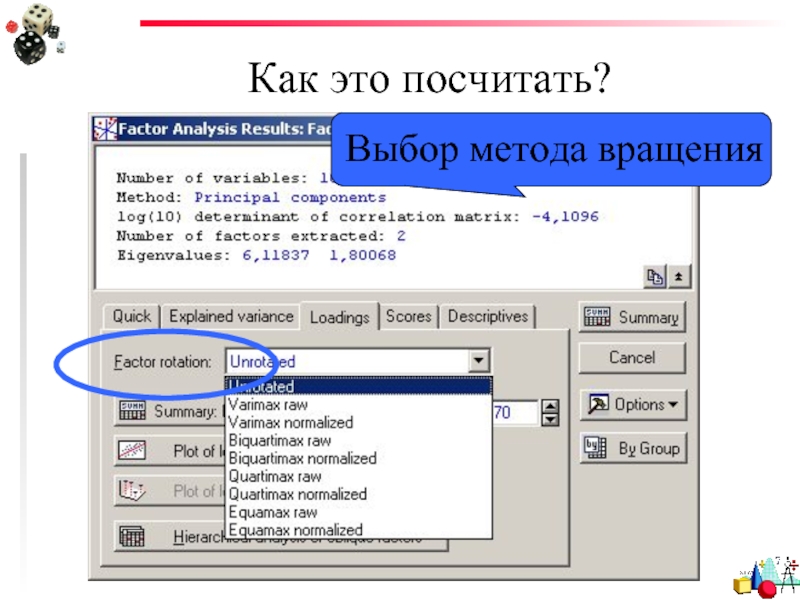
- 60. Как это посчитать? Выбор метода вращения
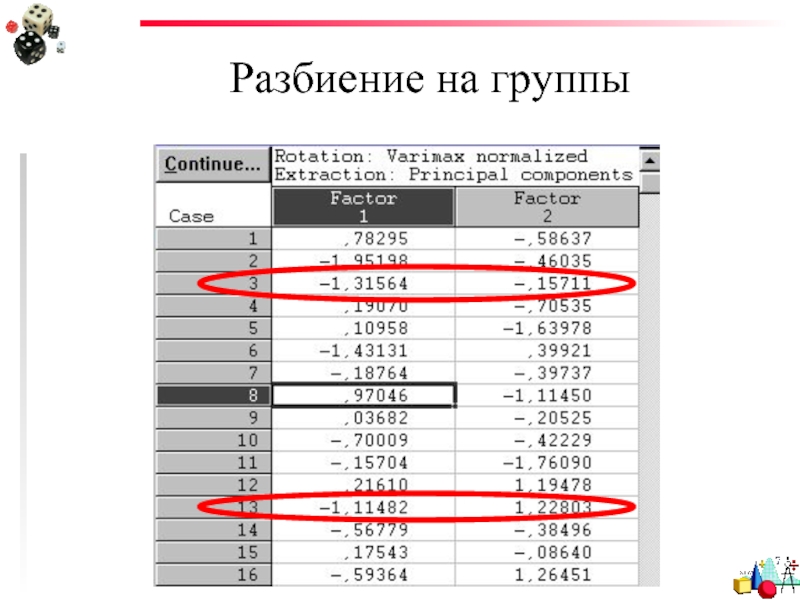
- 61. Разбиение на группы Если факторы найдены и
- 62. Разбиение на группы Таким образом, для каждого
- 63. Разбиение на группы
- 64. Разбиение на группы
- 65. Разбиение на группы Если факторов больше или
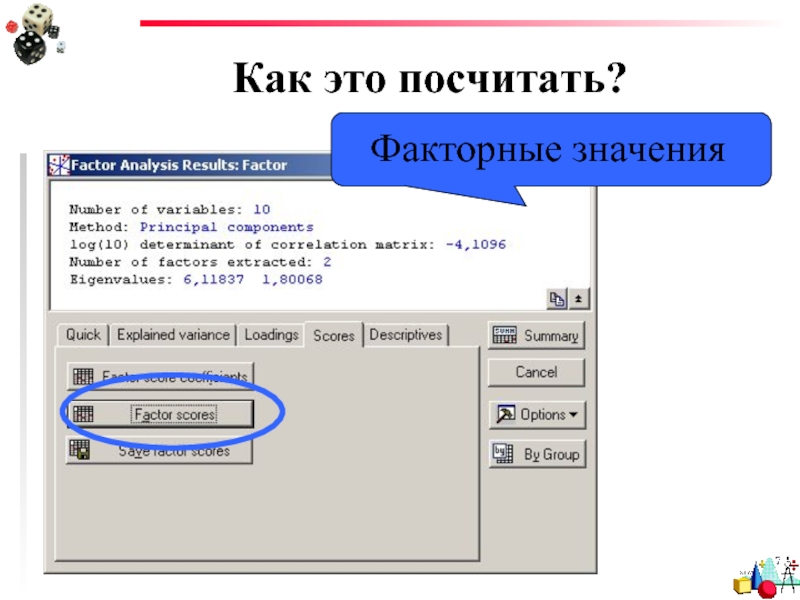
- 66. Как это посчитать? Факторные значения
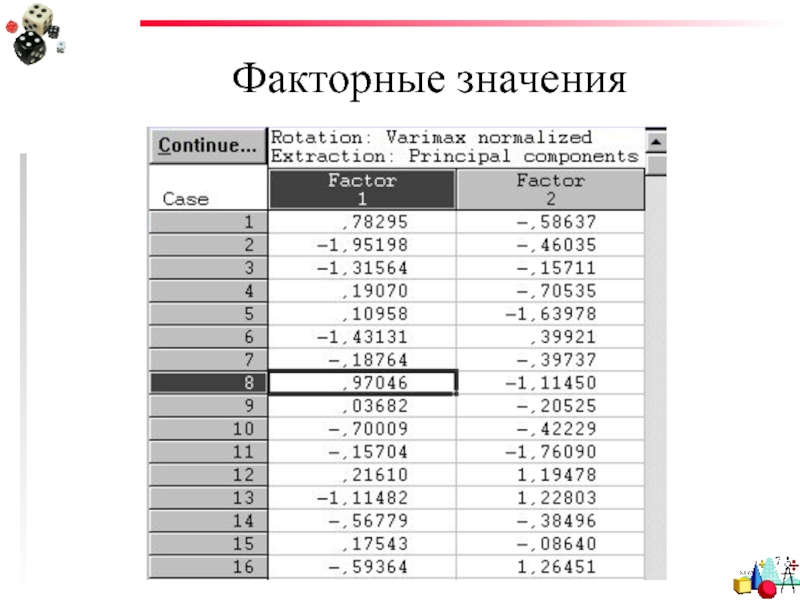
- 67. Факторные значения
- 68. Факторный анализ Наиболее плодотворно использование факторного анализа
- 69. Удачные примеры (с моей т.з.) Адаптация теста (психодиагностичекой методики) Исследование семантических пространств
- 70. Удачные примеры Измерение личностных особенностей
- 71. Удачные примеры Измерение личностных особенностей
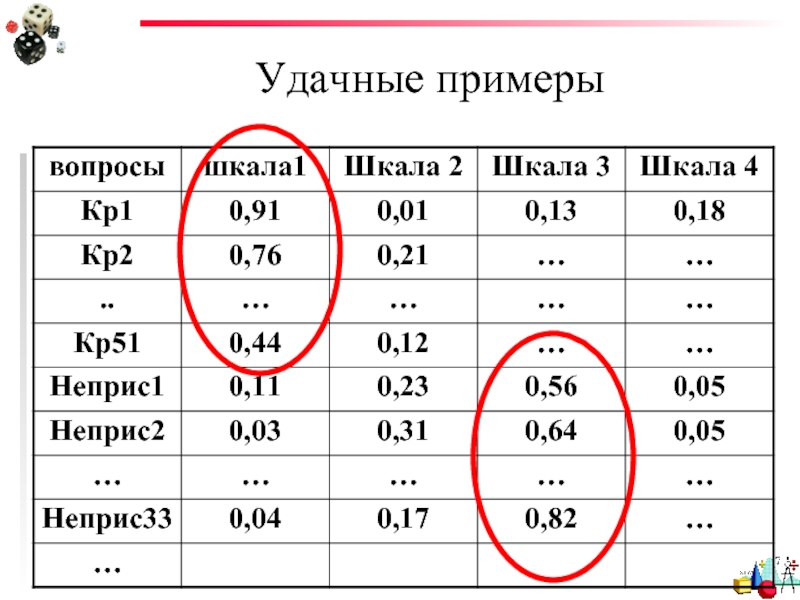
- 72. Удачные примеры
- 73. Удачные примеры Семантический дифференциал (например, у В.Ф.
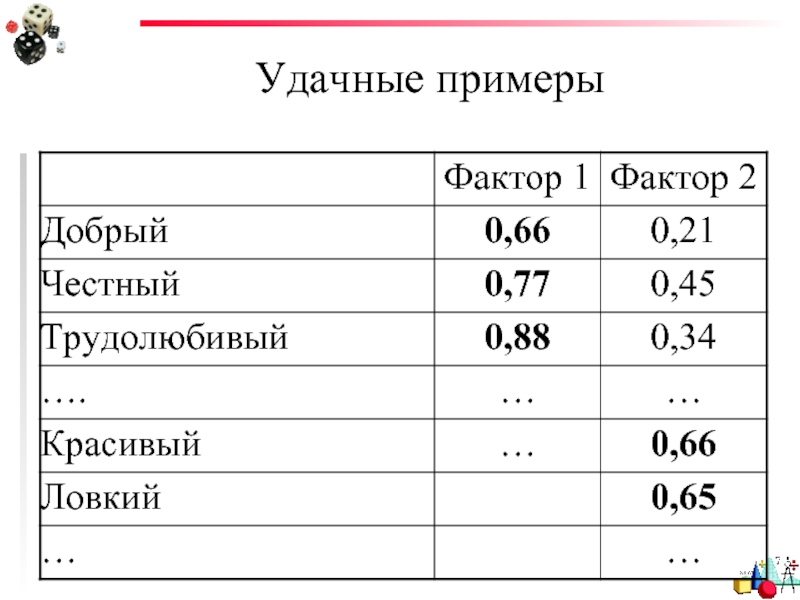
- 74. Удачные примеры
- 75. Удачные примеры
- 76. Требования и ограничения ФА Нормальное распределение
- 77. Что представляем в статье? Обычно дается
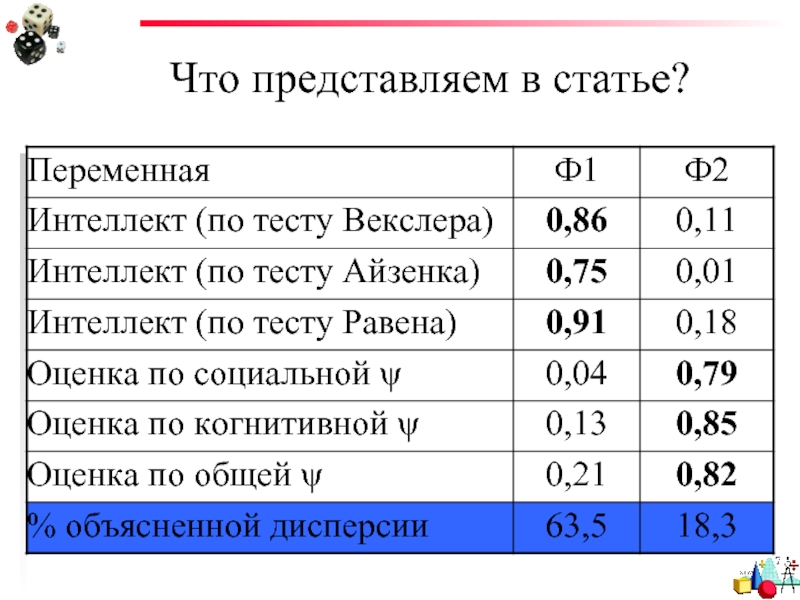
- 78. Что представляем в статье?
- 79. Что такое КМО? КМО - это
- 80. Что такое КМО? Bartlett's Test of
- 81. Полезная литература Просто и доходчиво факторный анализ
- 82. Полезная литература ПРОГРАММА STATISTICA Боровиков В. Программа
- 83. Факторный анализ СПАСИБО ЗА ВНИМАНИЕ!
- 84. Факторный анализ Это все был только эксплораторный факторный анализ!
- 85. Конфирматорный ФА Основная идея: Вы сами
- 86. Конфирматорный ФА В STATISTICA 6.0 Statistics
- 87. Конфирматорный ФА
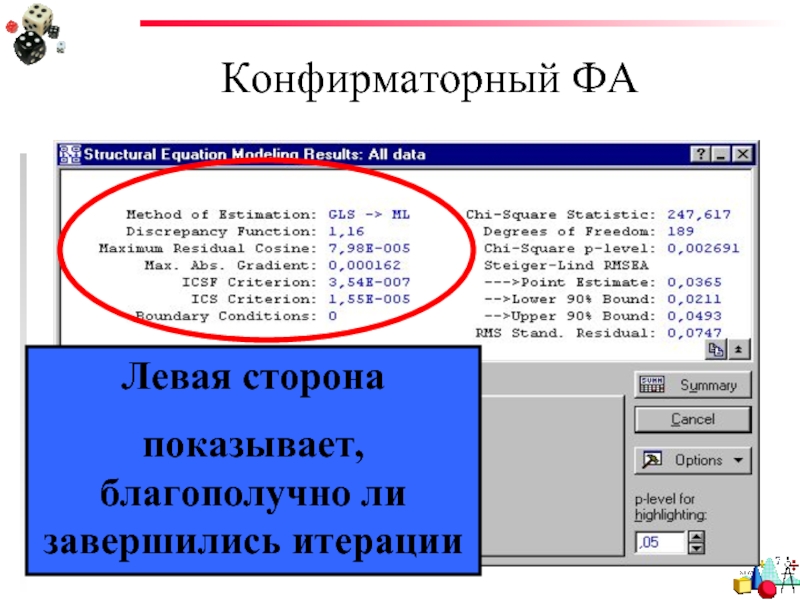
- 88. Конфирматорный ФА Левая сторона показывает, благополучно ли завершились итерации
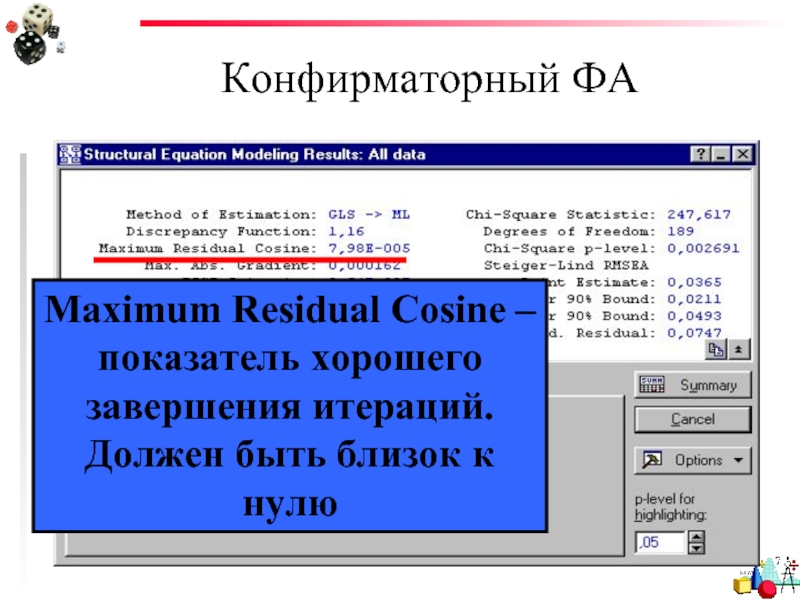
- 89. Конфирматорный ФА Maximum Residual Cosine – показатель хорошего завершения итераций. Должен быть близок к нулю
- 90. Конфирматорный ФА Maximum Absolute Constraint Тоже показатель
- 91. Конфирматорный ФА ICSF Criterion. и ICS
- 92. Конфирматорный ФА Boundary Conditions. Должен
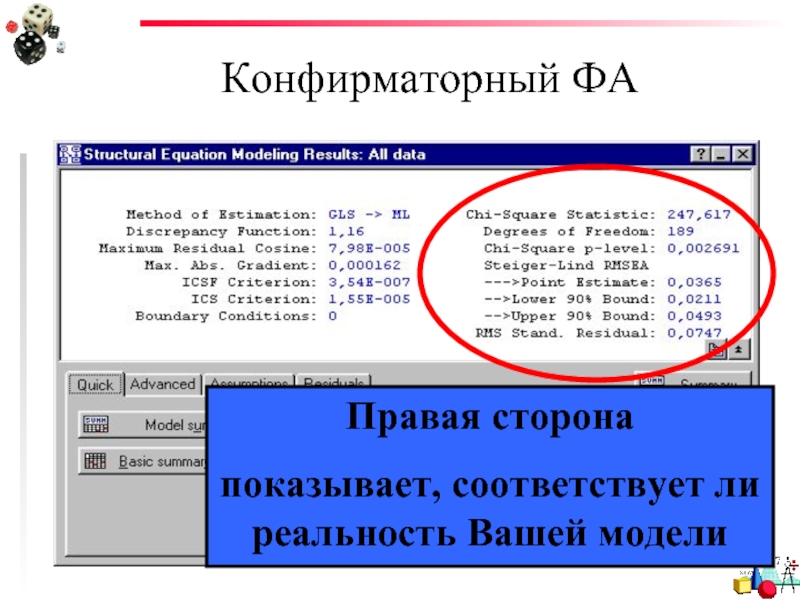
- 93. Конфирматорный ФА Правая сторона показывает, соответствует ли реальность Вашей модели
- 94. Конфирматорный ФА Chi-square Statistic Проверяет нуль-гипотезу об идеальном соответствии
- 95. Конфирматорный ФА RMS Standardized Residual Этот
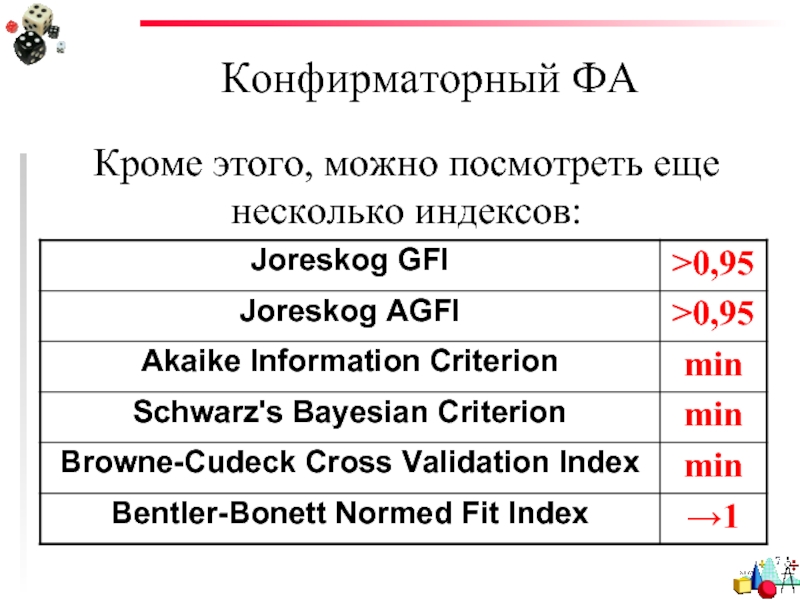
- 96. Конфирматорный ФА Кроме этого, можно посмотреть еще несколько индексов:
- 97. Полезная литература К практическому занятию по ФА
- 98. СПАСИБО ЗА ТЕРПЕНИЕ!
Слайд 2Факторный анализ
Факторный анализ – как религия: каждый находит в нем что-то
Под факторным анализом понимают два метода:
Метод главных компонент
Факторный анализ
Слайд 3Основная идея
Метод главных компонент объясняет наибольшую вариативность в терминах наименьшего количества
Слайд 4Основная идея
Факторный анализ объясняет отношения между переменными с помощью нескольких факторов,
Слайд 5Основная идея
Оба метода основываются на корреляциях (или ковариациях) между исходными переменными
Слайд 6Основная идея
Главными целями факторного анализа являются: (1) сокращение числа переменных и
Слайд 7Метод главных компонент
– это метод, который переводит большое количество связанных между
Слайд 8Метод главных компонент
ПРИМЕР: у студентов измерили
интеллект по тесту Векслера,
интеллект по тесту Айзенка,
интеллект по тесту Равена,
а также
успеваемость по социальной ψ
успеваемость по когнитивной ψ
успеваемость по общей ψ.
Слайд 9Метод главных компонент
Если переменных в исследовании слишком много (x1, x2, …,
Слайд 10Метод главных компонент
Для этого и служит метод главных компонент, который создает
Слайд 11Метод главных компонент
y1=a11x1+a12x2+…+a1pxp
y2=a21x1+a22x2+…+a2pxp
… (1)
yp=ap1x1+ap2x2+…+appxp
Это и есть модель для метода главных компонент
Слайд 12Метод главных компонент
Переменные y1, y2, …, yp называются главными компонентами или
Таким образом, фактор – это искусственный статистический показатель, возникающий в результате специальных преобразований корреляционной матрицы.
Слайд 13Метод главных компонент
Процедура извлечения факторов называется факторизацией матрицы.(проведение ФА).
В результате
Слайд 14Метод главных компонент
Коэффициенты aij, определяющие новую переменную, выбираются таким образом, чтобы
Слайд 15Метод главных компонент
Часто полезно представить коэффициенты aij таким образом, чтобы они
Слайд 18Факторный анализ
Основное отличие между факторным анализом и методом главных компонент заключается
Слайд 19Факторный анализ
Модель факторного анализа предполагает, что корреляции между наблюдаемыми переменными x1,
Слайд 20Факторный анализ
Дисперсия исходных переменных здесь объясняется не в полном объеме: признается,
Слайд 21Факторный анализ
x1=λ11f1+ λ 12f2+…+ λ1kfk+u1
x2= λ21f1+ λ 22f2+…+ λ2kfk+u2
…
xp= λp1f1+ λ p2f2+…+ λpkfk+up
Это и есть модель факторного анализа
Слайд 22Факторный анализ
Случайная погрешность ui называется характерностью и представляет собой часть наблюдаемой
Слайд 23Факторный анализ
Общность (Communality) переменной xi - является той дисперсией, которую переменная
Дисперсия явной переменной может быть разделена на две части:
Характерность - часть единичной дисперсии переменной, которая не связана с общими факторами.
Слайд 24Факторный анализ
Если латентные факторы не коррелируют, то коэффициенты λij являются корреляциями
Слайд 25Факторный анализ
Соответствие факторной модели полученным данным проверяется путем сравнения исходной корреляционной
Слайд 27Факторный анализ
Commonalities=multiple R-square.
Если выбран этот метод, то перед факторизацией диагональные
Слайд 28Факторный анализ
Iterated commonalities (MINRES).
Этот метод отличается от предыдущего тем, что
Слайд 29Факторный анализ
Maximum likelihood factors
метод максимального правдоподобия Д. Лоули. В отличие
Слайд 30Факторный анализ
Centroid method
– центроидный метод Л. Тэрстоуна. В нем корреляции
Слайд 31Факторный анализ
Principal axis method
В этом методе (методе главных осей) на
Слайд 32Факторный анализ
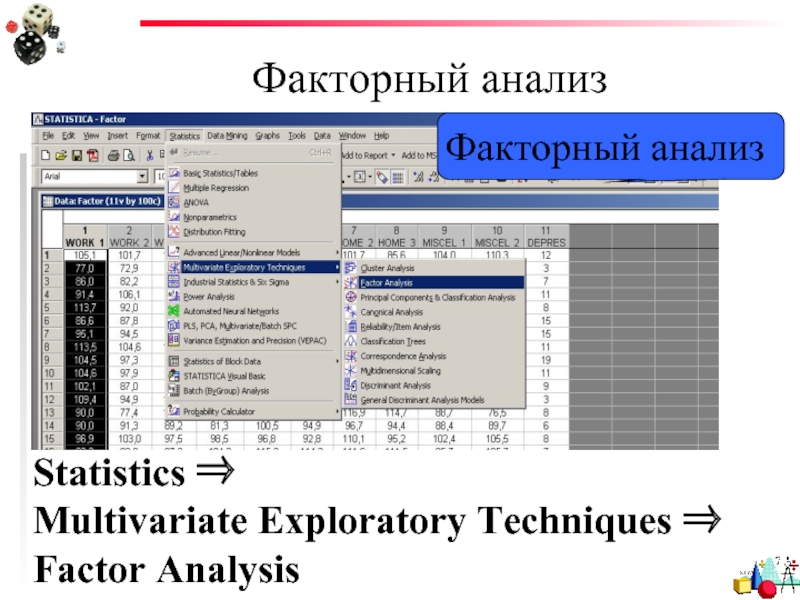
Факторный анализ
Statistics ⇒
Multivariate Exploratory Techniques ⇒ Factor Analysis
Слайд 35Факторный анализ
☺ Но! Факторные отображения одной и той же корреляционной матрицы
Практически это значит, что вы получите одни и те же результаты при любом методе.
Слайд 36Факторный анализ
Результаты, полученные с помощью метода главных компонент, и результаты, полученные
☺
Слайд 37Сколько факторов?
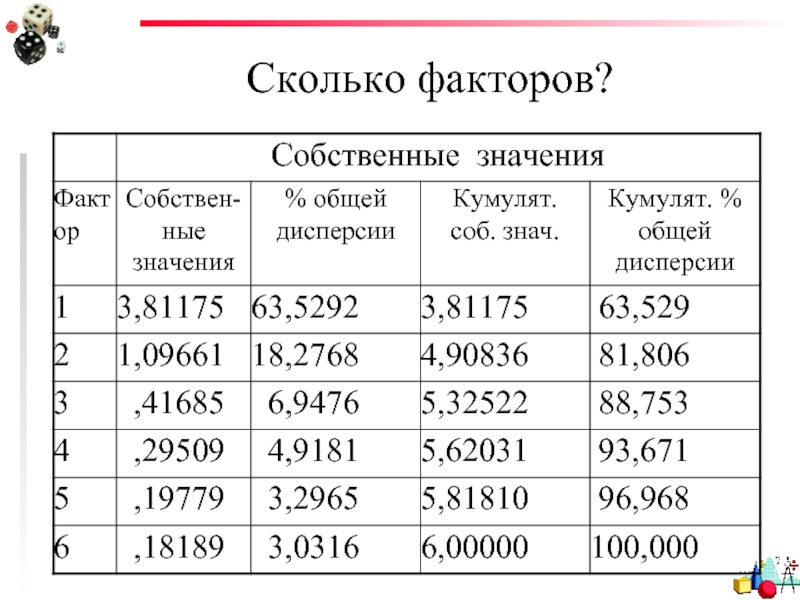
Для применения процедуры выбора следует посчитать некоторую статистику – собственные
Слайд 39Сколько факторов?
1) Процент объясненной дисперсии. Если кумулятивный (накопленный) процент общей дисперсии
Слайд 41Сколько факторов?
2) Критерий Кайзера (H. Keiser). Вы можете отобрать только факторы
Слайд 43Сколько факторов?
3) Критерий каменистой осыпи является графическим методом. Вы можете изобразить
Слайд 45Сколько факторов?
4) На практике возникает важный дополнительный вопрос, а именно: когда
☺
Слайд 46Вращение матрицы факторных нагрузок
Оказывается, что описанные выше шаги не дают однозначного
Слайд 47Вращение матрицы факторных нагрузок
Необходимость вращения факторов возникает чаще всего, когда выявленным
Слайд 48Вращение матрицы факторных нагрузок
В программе STATISTICA:
Варимакс (Varimax) – это такое ортогональное
Слайд 49Вращение матрицы факторных нагрузок
Квартимакс (Quartimax) – ортогональное вращение, при котором происходит
Слайд 50Вращение матрицы факторных нагрузок
Биквартимакс (Biquartimax) –метод, который является компромиссом между варимаксом
Слайд 51Вращение матрицы факторных нагрузок
Эквамакс (Equamax) – тоже является компромиссом между варимаксом
Слайд 52Алгоритм факторного анализа
Заносим данные в программу.
Выбираем метод - анализ главных компонент
Слайд 53Алгоритм факторного анализа
Выбираем количество факторов.
Строим матрицу факторных нагрузок.
Вращаем матрицу факторных нагрузок.
Интерпретируем
Слайд 54Алгоритм факторного анализа
Если ничего не получается, то можно попробовать разные способы
Если это ничего не дает, то можно попробовать взять разное количество факторов (возвращаемся на п. 3)
Если и это ничего не дает, то можно попробовать взять другой метод (возвращаемся на п. 2)
Слайд 61Разбиение на группы
Если факторы найдены и истолкованы, то на последнем шаге
Слайд 62Разбиение на группы
Таким образом, для каждого наблюдения значения большого количества переменных
Слайд 65Разбиение на группы
Если факторов больше или введены дополнительные градации (плохо учится
Слайд 68Факторный анализ
Наиболее плодотворно использование факторного анализа на ранних стадиях исследования
Факторный анализ
Слайд 69Удачные примеры (с моей т.з.)
Адаптация теста (психодиагностичекой методики)
Исследование семантических пространств
Слайд 70Удачные примеры
Измерение личностных особенностей (по Иванову для взрослых)
Шкалы:
Кривизны
Неприспособленности
Неудачливости
Нужды в
Слайд 71Удачные примеры
Измерение личностных особенностей (по Иванову для взрослых)
Шкала кривизны
Насколько
Как часто над Вами смеются?
…
Слайд 73Удачные примеры
Семантический дифференциал
(например, у В.Ф. Петренко «Основы психосемантики»)
Баба Яга
Добрая – Злая
Красивая
Ленивая – Трудолюбивая
…
Слайд 76Требования и ограничения ФА
Нормальное распределение всех переменных
Все наблюдения независимы
По крайней
Т.е. данные должны быть такими, которые подходят для подсчета к-та корреляции Пирсона
Слайд 77Что представляем в статье?
Обычно дается матрица факторных нагрузок после вращения
+ ВАША ИНТЕРПРЕТАЦИЯ!
Слайд 79Что такое КМО?
КМО - это показатель Кайзера и его коллег:
Мера выборочной адекватности
Это % дисперсии, который объясняют общие (латентные) факторы
Должен быть > 0,5
KMO and Bartlett's Test of Sphericity –
есть в SPSS, но нет в Statistica
Слайд 80Что такое КМО?
Bartlett's Test of Sphericity –
проверяет, является ли матрица
Т.е. этот тест д.б. значимым!
KMO and Bartlett's Test of Sphericity –
есть в SPSS, но нет в Statistice
Слайд 81Полезная литература
Просто и доходчиво факторный анализ изложен в
Гусев А.Н., Измайлов
Ермолаев О.Ю. Математическая статистика для психологов: Учебник/ - 2-е изд., испр. – М.: Московский психолого-социальный институт: Флинта, 2003.
Электронный учебник по ФА (Радчикова Н., Радчиков А.)
Слайд 82Полезная литература
ПРОГРАММА STATISTICA
Боровиков В. Программа STATISTICA для студентов и инженеров. -
Электронный учебник по программе (StatSoft)
ПРОГРАММА SPSS
Наследов А.Д. Математические методы психологического исследования. Анализ и интерпретация данных. – СПб. – Речь. – 2004.
Бююль А., Цефель П. SPSS: Искусство обработки информации. – СПб, «ЛиаСофтЮп». –2001.