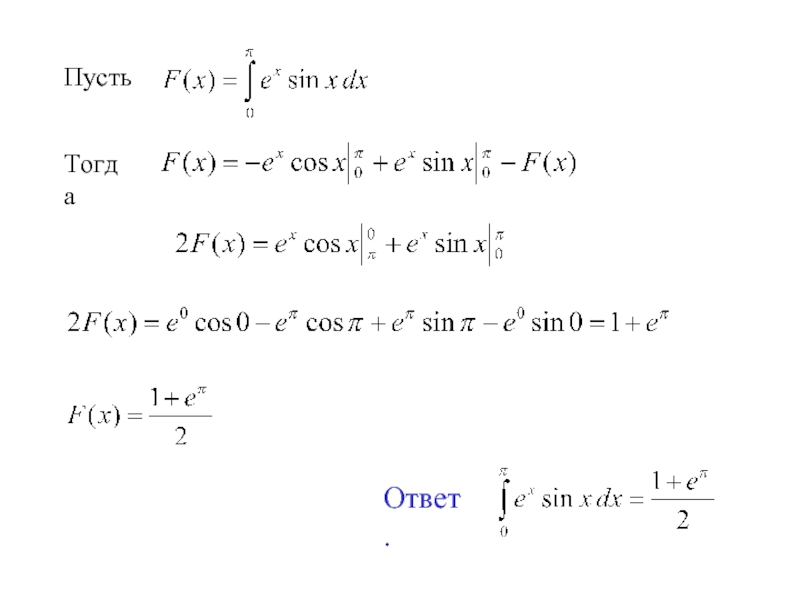- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определенный интеграл презентация
Содержание
- 1. Определенный интеграл
- 2. x y 0 a b y =
- 3. x y 0 a=x0 b=xn y =
- 4. x y 0 a=x0 b=xn y =
- 5. x y 0 a=x0 b=xn y =
- 6. x y 0 a b y =
- 7. - определённый интеграл - подынтегральная функция -
- 8. Свойства определённого интеграла. 10.
- 9. 20. Определённый интеграл от алгебраической суммы двух
- 10. 40. Если функция f(x) интегрируема на [a;b] и a
- 11. Формула Ньютона-Лейбница знак двойной подстановки
- 12. Метод непосредственного интегрирования. Пример 1. Вычислить интеграл Ответ. 2
- 13. Пример 2. Вычислить интеграл Ответ. 4
- 14. Метод подстановки (метод замены переменной).
- 15. Если непрерывны на отрезке определена и непрерывна на отрезке то
- 16. Замечание. 1) При вычислении определённого интеграла методом
- 17. Пример 3. Вычислить интеграл Ответ.
- 18. Пример 4. Вычислить интеграл Ответ.
- 19. Пример 5. Вычислить интеграл Ответ.
- 20. Метод интегрирования по частям. Теорема.
- 21. Пример 6. Вычислить интеграл
- 22. Пример 7. Вычислить интеграл
- 23. Пусть Тогда Ответ.
Слайд 2x
y
0
a
b
y = f(x)
Криволинейная трапеция- это фигура, ограниченная графиком непрерывной неотрицательной функции
x = a
x = b
Пусть y = f(x) непрерывная функция на отрезке [a;b]
Криволинейная трапеция. Понятие определённого интеграла.
Слайд 3x
y
0
a=x0
b=xn
y = f(x)
Найдём площадь криволинейной трапеции.
1) Разобъем отрезок [a;b] точками xi
2) Пусть длина отрезка
3) Проведём через точки xi прямые, параллельные оси ОУ.
x1
xi-1
xi
xn-1
4) В каждом отрезке [xi-1;xi] возьмём произвольную точку ξi и вычислим значение функции в ней, т.е. f(ξi)
Слайд 4x
y
0
a=x0
b=xn
y = f(x)
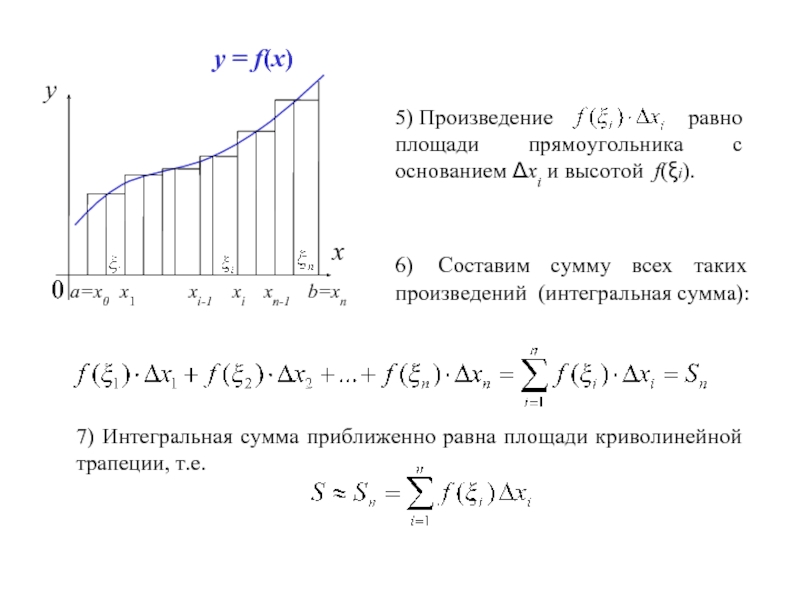
5) Произведение равно площади
6) Составим сумму всех таких произведений (интегральная сумма):
x1
xi-1
xi
xn-1
7) Интегральная сумма приближенно равна площади криволинейной трапеции, т.е.
Слайд 5x
y
0
a=x0
b=xn
y = f(x)
8) Пусть длина наибольшего из отрезков [
9) При интегральная сумма имеет предел
x1
xi-1
xi
xn-1
Слайд 6x
y
0
a
b
y = f(x)
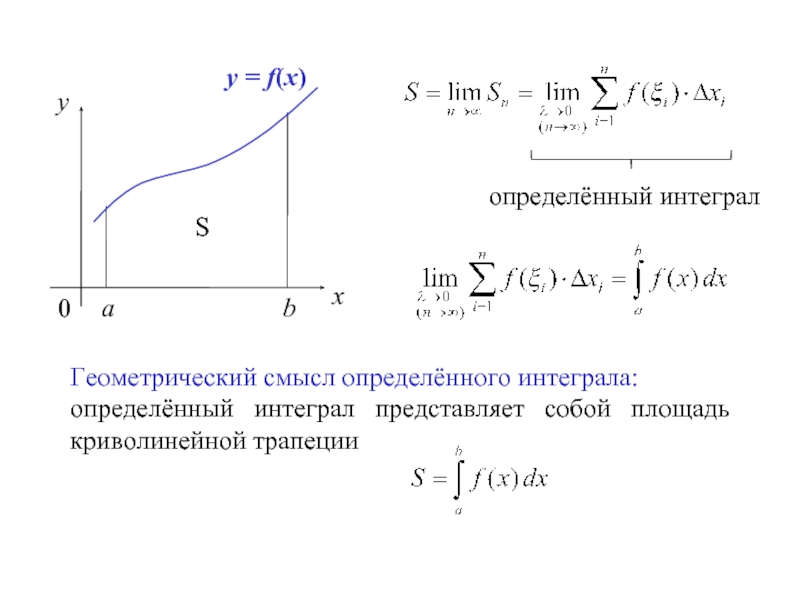
Геометрический смысл определённого интеграла:
определённый интеграл представляет собой площадь криволинейной
S
определённый интеграл
Слайд 7- определённый интеграл
- подынтегральная функция
- подынтегральное выражение
х – переменная интегрирования
a– нижний
b– верхний предел интегрирования
пределы интегрирования
Слайд 8Свойства определённого интеграла.
10. Постоянный множитель можно выносить за знак определённого интеграла:
Слайд 920. Определённый интеграл от алгебраической суммы двух или нескольких функций равен
30. При перестановке пределов интегрирования, знак интеграла меняется на противоположный, т.е.
Слайд 14Метод подстановки
(метод замены переменной).
Теорема.
Пусть дан интеграл
, где функция
непрерывна на отрезке [a;b].
Введём новую переменную
Слайд 16Замечание.
1) При вычислении определённого интеграла методом подстановки возвращаться к старой переменной
2) Часто вместо подстановки применяют подстановку ;
3) Не следует забывать менять пределы интегрирования при замене переменных!
Слайд 20Метод интегрирования по частям.
Теорема.
Если функции u = u(x) и v =
