- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы математической логики. Формулы алгебры логики презентация
Содержание
- 1. Элементы математической логики. Формулы алгебры логики
- 2. Логика высказываний Высказывания Истинность высказывания
- 3. КОНЪЮНКЦИЯ: бинарное Обозначается: ^ (логическое умножение, операция «и»)
- 4. ТАБЛИЦЫ ИСТИННОСТИ. СВОЙСТВА ОТРИЦАНИЕ: унарное
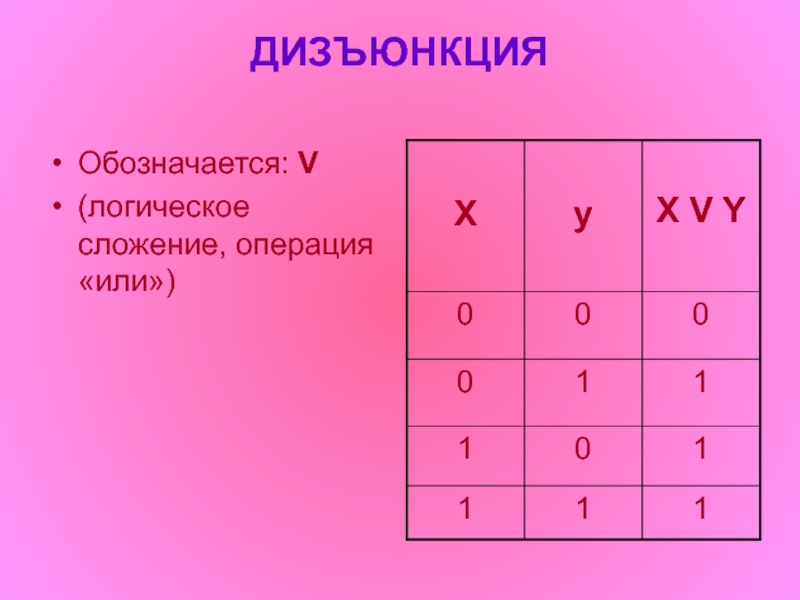
- 5. ДИЗЪЮНКЦИЯ Обозначается: V (логическое сложение, операция «или»)
- 6. ИМПЛИКАЦИЯ Обозначается: X →Y (Импликация двух
- 7. Эквиваленция Обозначается: X ↔ Y (Эквиваленция двух
- 8. Штрих Шеффера: Обозначается: X /Y (высказывание, которое
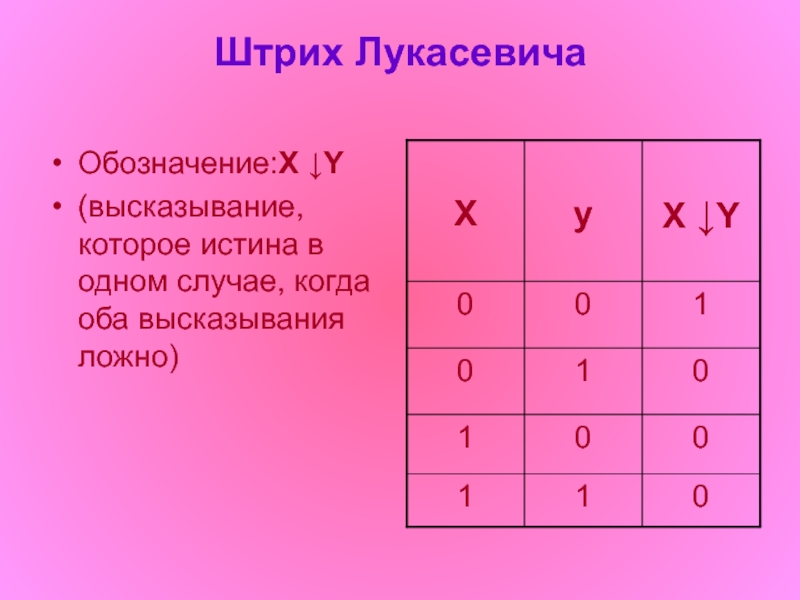
- 9. Штрих Лукасевича Обозначение:X ↓Y (высказывание, которое истина в одном случае, когда оба высказывания ложно)
- 10. формулы алгебры логики
- 11. Равносильные формулы Две формулы А и В
- 12. Основные равносильности алгебры логики 1. 2.
- 13. Равносильности выражающие одни логические функции через другие
- 14. Равносильности выражающие основные законы алгебры логики
Слайд 2
Логика высказываний
Высказывания
Истинность высказывания
Операции над высказываниями
Дизъюнкция
Конъюнкция
Импликация
Эквиваленция
Штрих Шеффера
Штрих Лукасевича
Слайд 4
ТАБЛИЦЫ ИСТИННОСТИ. СВОЙСТВА
ОТРИЦАНИЕ: унарное
Высказывание это: любое предложение, утверждающее что-либо, при
1-истина (и, true).
0-ложь (, false).
Высказывание, получаемое из элементарных с помощью связок: не, и, или, если то, тогда и только тогда - называются сложными или составными. Ни одно высказывание не может быть одновременно истинным или ложным.
Пример:
=
x = x (враг моего врага мой друг)
=
Двойное отрицание - x
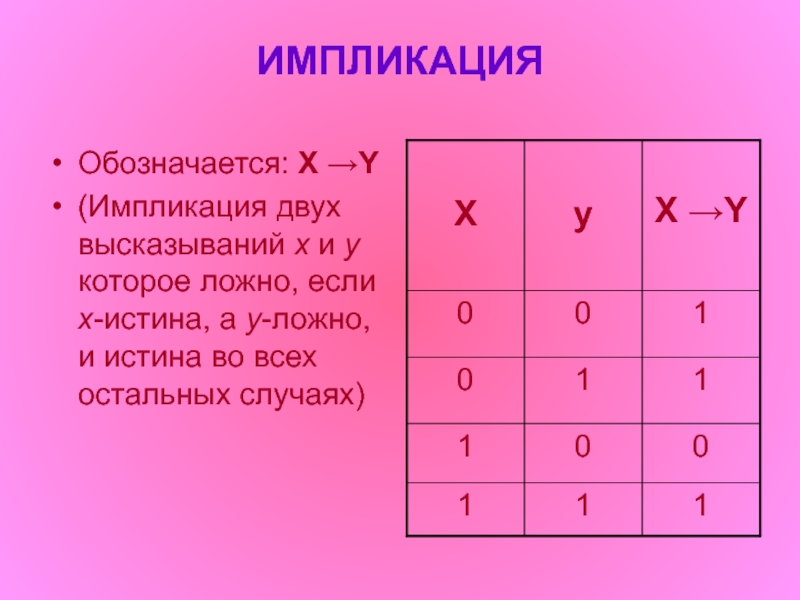
Слайд 6ИМПЛИКАЦИЯ
Обозначается: X →Y
(Импликация двух высказываний x и y которое ложно,
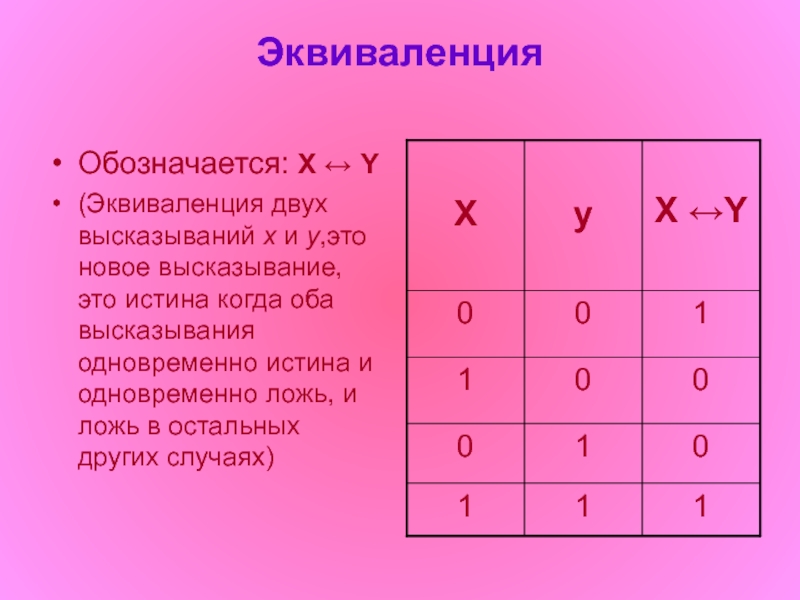
Слайд 7Эквиваленция
Обозначается: X ↔ Y
(Эквиваленция двух высказываний x и y,это новое высказывание,
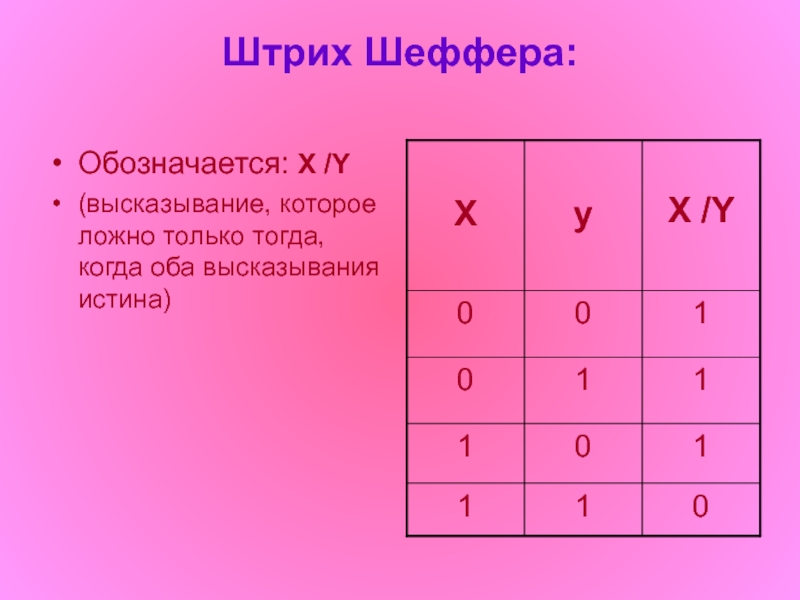
Слайд 8Штрих Шеффера:
Обозначается: X /Y
(высказывание, которое ложно только тогда, когда оба высказывания
Слайд 9Штрих Лукасевича
Обозначение:X ↓Y
(высказывание, которое истина в одном случае, когда оба высказывания
Слайд 11Равносильные формулы
Две формулы А и В равносильны, если они принимают одинаковые
А называется тождественно истинным высказыванием, если она принимает значение единицы при любом значении входящих переменных.
А называется тождественно ложной, если принимает значение нуля, при всех значениях входящих в неё переменных.
1. А≡В
= 3.
2. x≡x
Слайд 12Основные равносильности алгебры логики
1.
2.
3.
4.
5.
6.
7.
8. закон исключенного третьего
9. закон снятия двойного отрицания
10.а)
законы поглощения
в)
Слайд 14 Равносильности выражающие основные законы алгебры логики
1.
2.
3. закон ассоциативности конъюнкции
4. закон ассоциативности дизъюнкции
5.
6.
Итак, алгебра-логика обладает коммутативными и ассоциативными законами относительно операции конъюнкции и дизъюнкции и дистрибутивным законом конъюнкции относительно дизъюнкции.