- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы дисперсионного анализа презентация
Содержание
- 1. Элементы дисперсионного анализа
- 2. План Основные понятия Описание метода дисперсионного
- 3. Дисперсионный анализ (от латинского DISPERSIO – рассеивание
- 4. Фундаментальная концепция дисперсионного анализа предложена ФИШЕРОМ в
- 5. В дальнейшем выяснилась общенаучная значимость дисперсионного
- 6. Дисперсионный анализ — метод в математической статистике, направленный
- 7. 1. Основные понятия Сущность ДА заключается
- 8. К результативным признакам можно отнести: точно измеряемые
- 9. Фактор – это любое влияние, воздействие или
- 10. Факторы могут иметь различные ГРАДАЦИИ или различные
- 11. Фактор регулируемый Уровень
- 12. Виды дисперсионного анализа По
- 13. ДА несвязанных (различных, независимых) выборок.
- 14. ДА связанных выборок (зависимых).
- 15. дисперсионный анализ одномерный и многомерный (одна или несколько зависимых переменных)
- 16. Условия применения дисперсионного анализа
- 17. 2. Принцип применения метода дисперсионного анализа
- 18. Очевидно, что если регулируемый фактор ОКАЗЫВАЕТ влияние
- 19. Следовательно, ИЗМЕНЕНИЯ, вызванные влиянием контролируемого фактора будут
- 20. ОСНОВНАЯ ЗАДАЧА
- 21. Doбщ. - общая дисперсия наблюдаемых значений (вариант),
- 22. Dфакт - факторная (межгрупповая) дисперсия, характеризуется различием
- 23. D ост. - остаточная (внутригрупповая) дисперсия, которая
- 24. Этапы дисперсионного анализа Построение дисперсионного комплекса.
- 25. Замечание Для проверки нулевой гипотезы используется F-статистика
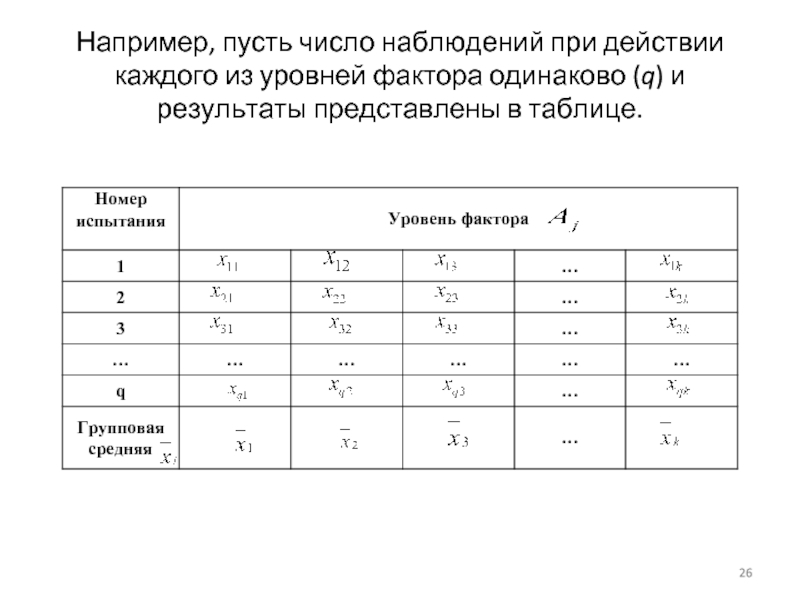
- 26. Например, пусть число наблюдений при действии каждого
- 27. Все значения величины х, наблюдаемые при каждом
- 28. Скорее всего выборочные средние
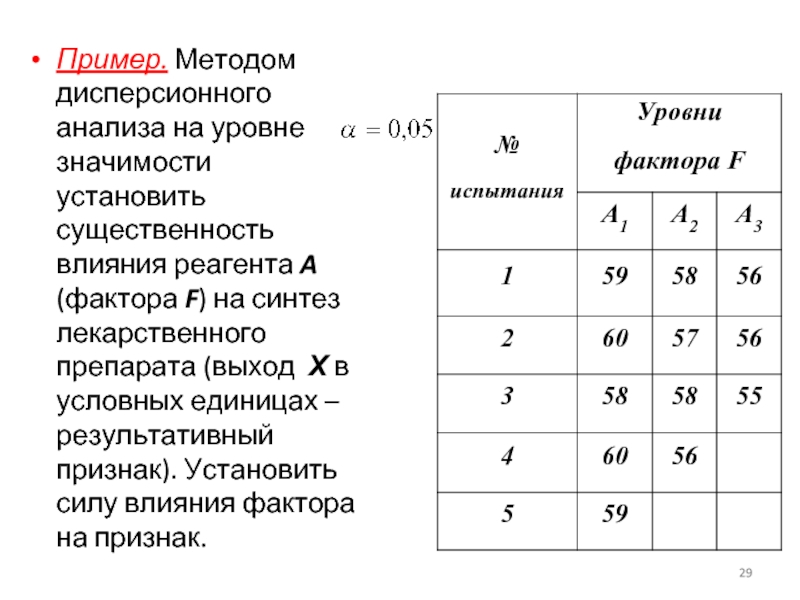
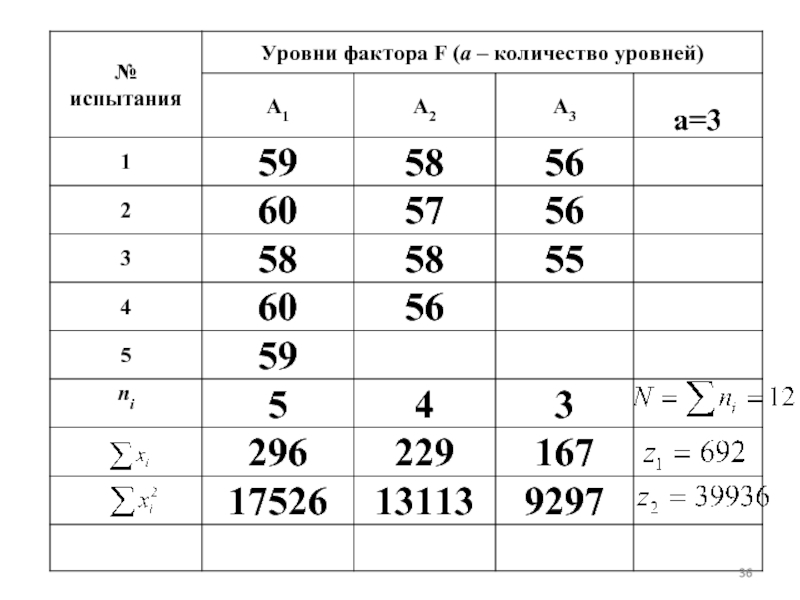
- 29. Пример. Методом дисперсионного анализа на
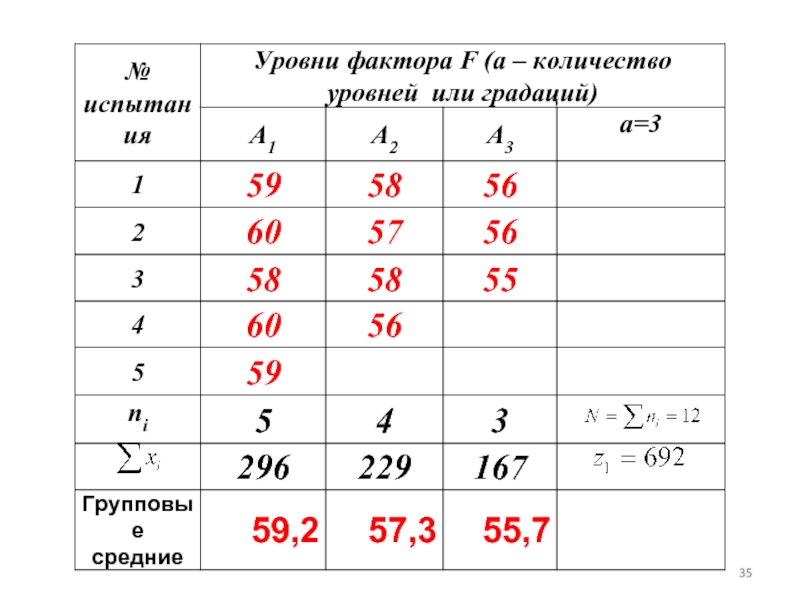
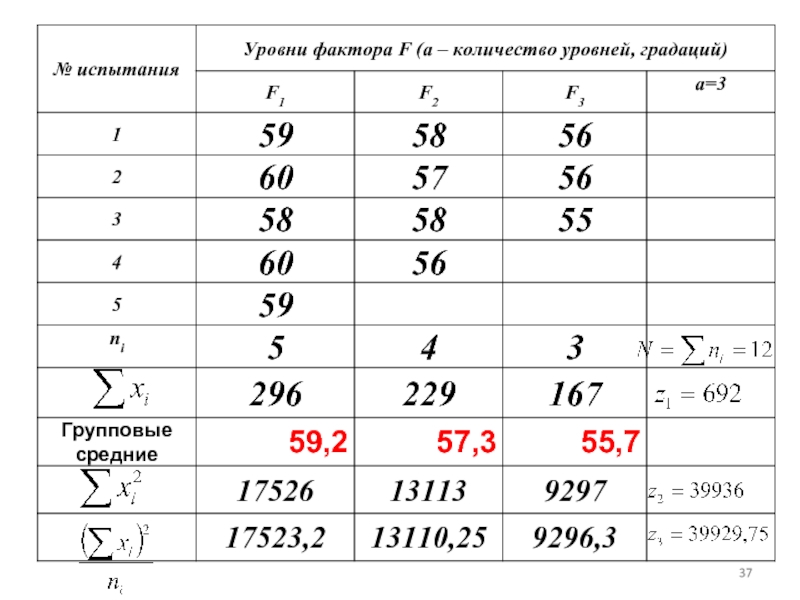
- 30. Найдем групповые среднии:
- 31. Выборочные средние по каждому уровню
- 32. Для проверки предположения о случайном различи средних воспользуемся методом дисперсионного анализа
- 33. ФОРМУЛЫ для вычислия сумм квадратов отклонений
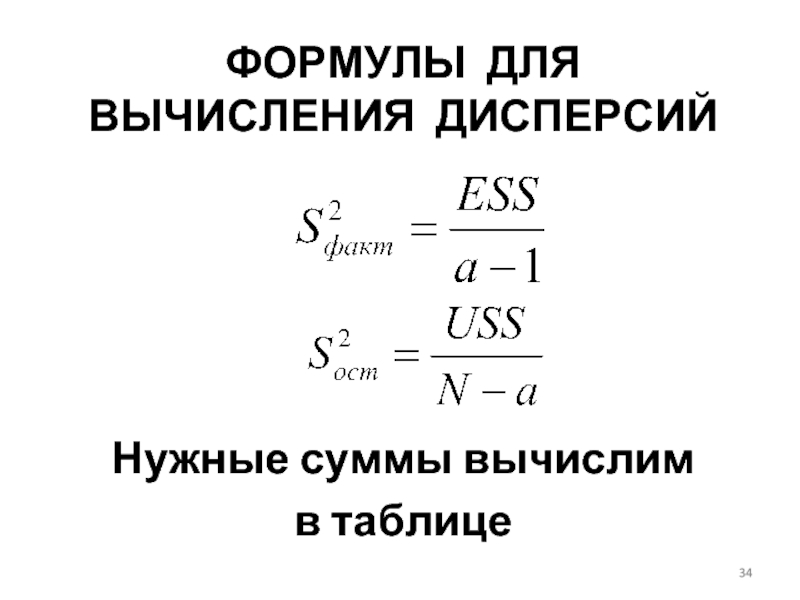
- 34. ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ ДИСПЕРСИЙ Нужные суммы вычислим в таблице
- 38. Вычислим суммы квадратов отклонений
- 39. Вычислим дисперсии
- 40. Сравнение факторной и остаточной дисперсий
- 41. Проверка гипотез для дисперсий. 1.
- 42. Проверим значимость различия дисперсий: найдем наблюдаемое значение
- 43. Вывод: дисперсии различаются значимо на уровне значимости
- 44. ОЦЕНИМ СИЛУ ВЛИЯНИЯ ФАКТОРА НА
- 45. Математики шутят ТЕОРВЕР БОЛЬШОЙ...
- 46. Потом спрашивает В. — А у тебя
Слайд 2План
Основные понятия
Описание метода дисперсионного анализа
Решение типовой задачи (однофакторный дисперсионный
несвязанных выборок)
Слайд 3Дисперсионный анализ (от латинского DISPERSIO – рассеивание / на английском Analysis
Рональд Эйлмер Фишер
( 1890 - 1962 )
Разработал:
дисперсионный анализ
теорию планирования эксперимента
метод максимального правдоподобия оценки параметров.
Слайд 4Фундаментальная концепция дисперсионного анализа предложена ФИШЕРОМ в 1920 году.
Первоначально дисперсионный
Метод применялся для оценки экспериментов в растениеводстве.
Слайд 5 В дальнейшем выяснилась общенаучная значимость дисперсионного анализа для экспериментов в
Возможно, более естественным был бы термин анализ суммы квадратов или анализ вариации, но в силу традиции употребляется термин дисперсионный анализ.
Слайд 6Дисперсионный анализ — метод в математической статистике, направленный на поиск зависимостей в
В отличие от t-критерия позволяет сравнивать средние значения трёх и более групп.
Слайд 71. Основные понятия
Сущность ДА заключается в изучении статистического влияния одного или
Результативные признаки — это те признаки, которые изменяются под влиянием факторных признаков.
Результативный признак – это элементарное качество или свойство объектов, изучаемое как результат влияния факторов: организованных в исследовании и всех остальных, неорганизованных в данном исследовании
Слайд 8К результативным признакам можно отнести:
точно измеряемые параметры объектов: рост, масса, АД,
неточно измеряемые параметры: умственные способности, например
комбинированные признаки
качественные признаки
Слайд 9Фактор – это любое влияние, воздействие или состояние, разнообразие которых может
Факторами могут быть
Физические воздействия (температура, влажность, радиация)
Химические воздействия: питание, стимуляторы, мутагены, алкоголь
Биологические: здоровье, болезни, наследственность, талантливость, идиотизм
Окружающая среда: ареал обитания, условия жизни
Возраст, пол и др.
Слайд 10Факторы могут иметь различные ГРАДАЦИИ или различные условия действия
Градация
Пример (шутка),
если отыщется исследователь, желающий определить зависимость яйценоскости от цвета курицы, то ничто не помешает ему применить дисперсионный анализ, и в качестве условий действия фактора «цвет» избрать, скажем, ЧЕРНЫХ, БЕЛЫХ И ПЕСТРЫХ кур.
Слайд 12Виды дисперсионного анализа
По количеству выявляемых регулируемых факторов дисперсионный анализ
однофакторным (при этом изучается влияние одного фактора на результаты эксперимента),
двухфакторным (при изучении влияния двух факторов)
многофакторным (позволяет оценить не только влияние каждого из факторов в отдельности, но и их взаимодействие).
Слайд 13ДА несвязанных (различных, независимых) выборок.
В зависимости от поставленной
Слайд 14ДА связанных выборок (зависимых).
Результаты воздействия факторов исследуются у
Слайд 16Условия применения
дисперсионного анализа
- выборочные данные должны быть взяты из
- исправленные выборочные дисперсии каждого уровня контролируемого фактора должны быть равны (оценки выборочных дисперсий)
- результаты наблюдений должны быть независимыми
Слайд 172. Принцип применения метода дисперсионного анализа
Формулируется
НУЛЕВАЯ ГИПОТЕЗА,
Слайд 18Очевидно, что если регулируемый фактор ОКАЗЫВАЕТ влияние на признак, то при
Слайд 19Следовательно, ИЗМЕНЕНИЯ, вызванные влиянием контролируемого фактора будут БОЛЕЕ ЗНАЧИМЫ, чем влияние
Оценить изменения можно с помощью дисперсий.
Слайд 20
ОСНОВНАЯ ЗАДАЧА
ДИСПЕРСИОННОГО АНАЛИЗА
заключается
Doбщ. = Dфакт + D ост
Слайд 21Doбщ. - общая дисперсия наблюдаемых значений (вариант), характеризуется разбросом вариант от
ОБЩЕЕ РАЗНООБРАЗИЕ СКЛАДЫВАЕТСЯ ИЗ МЕЖГРУППОВОГО И ВНУТРИГРУППОВОГО
Слайд 22Dфакт - факторная (межгрупповая) дисперсия, характеризуется различием средних в каждой группе
Например, в группах различных по этиологическому фактору клинического течения пневмонии средний уровень проведенного койко-дня неодинаков — наблюдается межгрупповое разнообразие.
Слайд 23D ост. - остаточная (внутригрупповая) дисперсия, которая характеризует рассеяние вариант внутри
Вариация изучаемого признака зависит от силы влияния каких-то неучтенных случайных факторов, как от организованных (заданных исследователем), так и от случайных (неизвестных) факторов.
Слайд 24Этапы дисперсионного анализа
Построение дисперсионного комплекса.
Вычисление квадратов отклонений.
Вычисление дисперсий.
Сравнение
Статистическая проверка нулевой гипотезы о несущественности различий факторной и остаточной дисперсий
Слайд 25Замечание
Для проверки нулевой гипотезы используется F-статистика
С помощью критерия Фишера-Снедекора можно
Слайд 26Например, пусть число наблюдений при действии каждого из уровней фактора одинаково
Слайд 27Все значения величины х, наблюдаемые при каждом фиксированном уровне фактора ,
Слайд 28
Скорее всего выборочные средние по каждому уровню будут отличаться
Выдвигаются две гипотезы:
Н0 – фактор не влияет на признак и, следовательно, средние значения величины признака на разных уровнях равны, т.е.
Н1 – фактор влияет на признак, и следовательно, хотя бы одно выборочное среднее значимо отличается от других.
Слайд 29
Пример. Методом дисперсионного анализа на уровне значимости
Слайд 31
Выборочные средние по каждому уровню отличаются друг от друга. Но
Выдвигаем нулевую гипотезу:
фактор не влияет на признак и, следовательно, средние значения величины признака на разных уровнях равны, т.е. H0:
Слайд 32Для проверки предположения
о случайном различи средних воспользуемся
методом
дисперсионного
Слайд 40
Сравнение факторной и остаточной дисперсий показывает, что
>
Прежде, чем делать окончательный вывод о влиянии фактора на признак, необходимо проверить статистическую значимость различий дисперсий
.
Слайд 41Проверка гипотез для дисперсий.
1. Нулевая гипотеза Н0 :
2. Конкурирующая гипотеза Н1: ≠
3. Для проверки нулевой гипотезы используем F-критерий Фишера
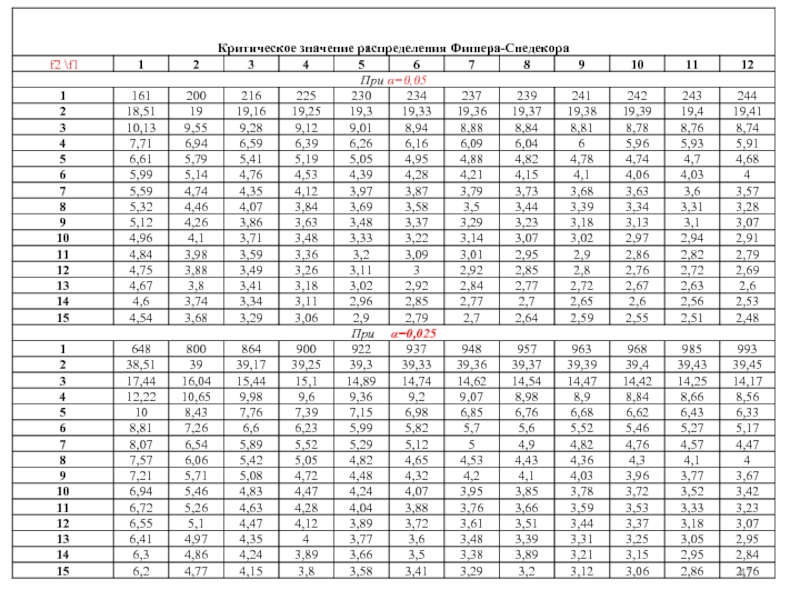
Слайд 42Проверим значимость различия дисперсий:
найдем наблюдаемое значение критерия различия:
найдем табличное значение
Сравним и
Слайд 43Вывод: дисперсии различаются значимо на уровне значимости 0,05 . Следовательно, фактор
Слайд 44
ОЦЕНИМ СИЛУ ВЛИЯНИЯ ФАКТОРА НА ПРИЗНАК
Вывод: Изменения признака (выхода
Слайд 45Математики шутят
ТЕОРВЕР БОЛЬШОЙ...
Во время сессии в
— Ну, как студенты? — спрашивает В. — Нормально сдают?
— Да как сказать, — мнется К. — Вот сейчас мне сдавал один студент. По билету ничего не сказал, на дополнительные вопросы не ответил. Но я ему все-таки поставил «четыре».
— Как?! За что? — поражается собеседник. — Он же ничего не знает!
— Теорвер большой, — задумчиво отвечает К. — что-нибудь да знает...
Слайд 46Потом спрашивает В.
— А у тебя как студенты?
— Да тоже не
— Но почему?! — теперь уже поражается К.
— Теорвер большой, — невозмутимо говорит В., — что-нибудь да не знает.