- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы аналитической геометрии. Линии первого порядка. (Лекция 7) презентация
Содержание
- 1. Элементы аналитической геометрии. Линии первого порядка. (Лекция 7)
- 2. План лекции Линии и их уравнения. Линии первого порядка.
- 3. 1. Линии и их уравнения
- 4. 1. Линии и их уравнения Опр. Равенство
- 5. 1. Линии и их уравнения Опр. Уравнение
- 6. 1. Линии и их уравнения Примеры
- 7. 1. Линии и их уравнения По заданному
- 8. 2. Линии первого порядка
- 9. 2. Линии первого порядка Уравнение прямой с
- 10. 2. Линии первого порядка Уравнение прямой с
- 11. Уравнение прямой с угловым коэффициентом
- 12. 2. Линии первого порядка Уравнение прямой с
- 13. Уравнение прямой, проходящей через данную точку, с
- 14. Уравнение прямой, проходящей через две данные точки
- 15. Уравнение прямой, проходящей через две данные точки
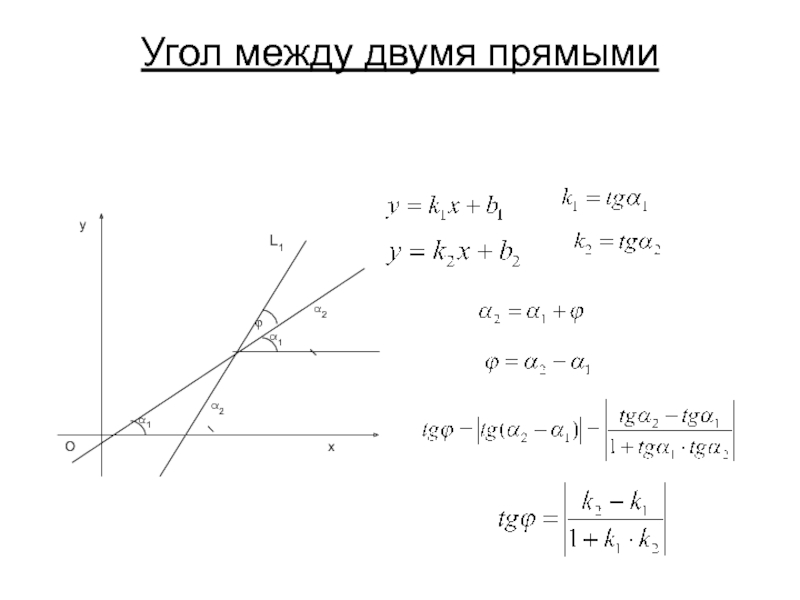
- 16. Угол между двумя прямыми
- 17. Условия параллельности и перпендикулярности прямых Если прямые
- 18. Общее уравнение прямой Теорема. В прямоугольной системе
- 19. Общее уравнение прямой Опр. Линии, определяемые уравнением первой степени, называются линиями первого порядка.
- 20. Общее уравнение прямой Таким образом, каждая прямая
- 21. Общее уравнение прямой Опр. Уравнение вида Ax+By+C=0 называется общим уравнением прямой (или полным уравнением прямой).
- 22. Неполное уравнение первой степени. Уравнение прямой «в
- 23. Неполное уравнение первой степени. Уравнение прямой «в
- 24. Неполное уравнение первой степени. Уравнение прямой «в
- 25. Неполное уравнение первой степени. Уравнение прямой «в
- 26. Нормальное уравнение прямой
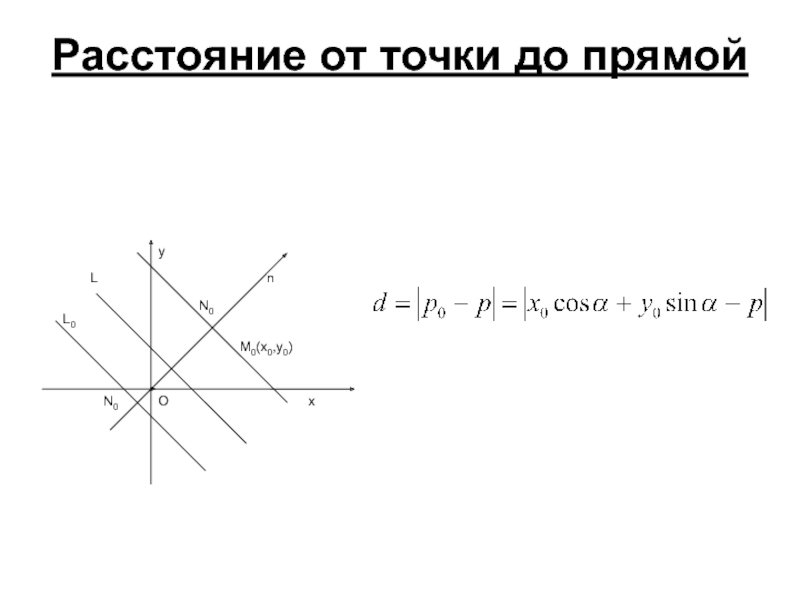
- 27. Расстояние от точки до прямой
- 28. Метод приведения общего уравнения прямой к нормальному
План лекции Линии и их уравнения. Линии первого порядка.
Слайд 41. Линии и их уравнения
Опр. Равенство вида F(x,y)=0 будем называть уравнением
с двумя переменными x и y, если это равенство справедливо не для всех пар чисел x и y.
Слайд 51. Линии и их уравнения
Опр. Уравнение F(x,y)=0 называется уравнением линии L
(относительно заданной системы координат), если этому уравнению удовлетворяют координаты x и y любой точки, лежащей на линии L, и не удовлетворяют координаты никакой точки, не лежащей на линии L.
Слайд 61. Линии и их уравнения
Примеры
x- y=0
x= y – прямая, биссектриса
1 и 3 координатных четвертей;
x2- y2=0
x- y=0
x+y=0, т.е. две прямые;
x2+y2=0 Этому уравнению удовлетворяет одна точка (0,0). Такую линию называют вырожденной;
x2+y2+1=0 – решений у этого уравнения нет, т.е. никакого геометрического образа на плоскости данное уравнение не определяет.
x2- y2=0
x- y=0
x+y=0, т.е. две прямые;
x2+y2=0 Этому уравнению удовлетворяет одна точка (0,0). Такую линию называют вырожденной;
x2+y2+1=0 – решений у этого уравнения нет, т.е. никакого геометрического образа на плоскости данное уравнение не определяет.
Слайд 71. Линии и их уравнения
По заданному множеству точек, т.е. заданной линии
L, найти ее уравнение F(x,y).
Пример
Пример
Слайд 92. Линии первого порядка
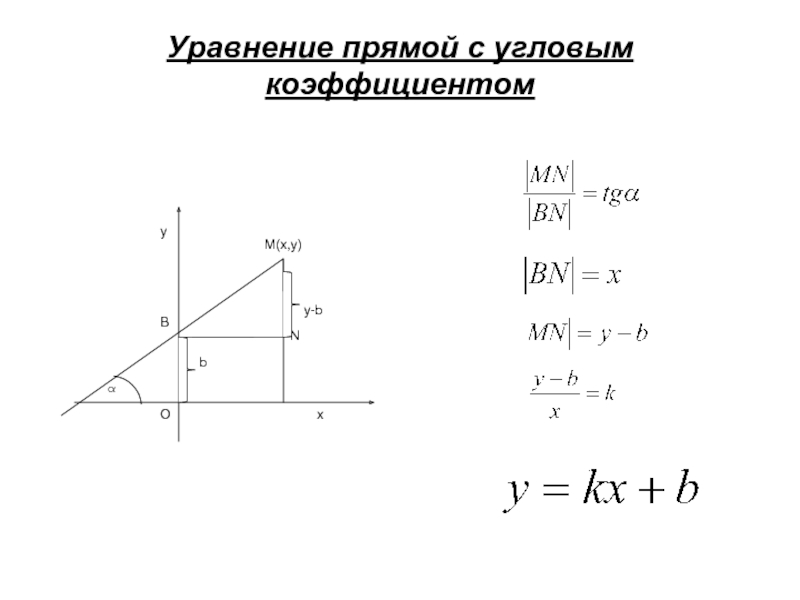
Уравнение прямой с угловым коэффициентом
Опр. Пусть дана некоторая
прямая не перпендикулярная оси Ox. Назовем углом наклона данной прямой к оси Ox угол α, на который нужно повернуть ось Ox против часовой стрелки, чтобы она совпала с прямой.
Слайд 102. Линии первого порядка
Уравнение прямой с угловым коэффициентом
Опр. Тангенс угла наклона
прямой к оси Ox называется угловым коэффициентом этой прямой и обозначается через k, т.е.
Слайд 122. Линии первого порядка
Уравнение прямой с угловым коэффициентом
Итак, любая прямая, не
перпендикулярная к оси Ox, определяется уравнением вида .
Верно и обратное, любое уравнение вида определяет прямую, которая имеет угловой коэффициент k и отсекает на оси Oy отрезок величины b.
Верно и обратное, любое уравнение вида определяет прямую, которая имеет угловой коэффициент k и отсекает на оси Oy отрезок величины b.
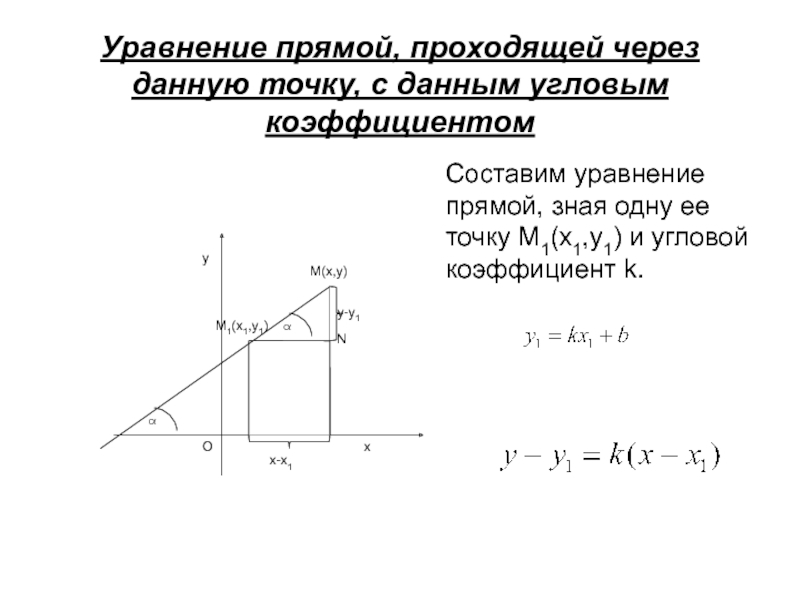
Слайд 13Уравнение прямой, проходящей через данную точку, с данным угловым коэффициентом
Составим уравнение
прямой, зная одну ее точку M1(x1,y1) и угловой коэффициент k.
Слайд 14Уравнение прямой, проходящей через две данные точки
Пусть даны две точки M1(x1,y1)
и M2(x2,y2). Принимая в
точку M(x,y) за M2(x2,y2), получим
Далее, если , то это уравнение можно записать в виде
Если же , то уравнение искомой прямой принимает вид y=y1.
точку M(x,y) за M2(x2,y2), получим
Далее, если , то это уравнение можно записать в виде
Если же , то уравнение искомой прямой принимает вид y=y1.
Слайд 15Уравнение прямой, проходящей через две данные точки
Замечание.
Если x1=x2, то прямая, проходящая
через точки M1(x1,y1) и M2(x2,y2), параллельна оси Oy и ее уравнение имеет вид x=x1.
Слайд 17Условия параллельности и перпендикулярности прямых
Если прямые L1 и L2 параллельны, то
φ=0 и tg φ=0.
Таким образом, условием параллельности двух прямых является равенство их угловых коэффициентов k2=k1
Если прямые L1 и L2 перпендикулярны между собой, т.е.
Таким образом, условием параллельности двух прямых является равенство их угловых коэффициентов k2=k1
Если прямые L1 и L2 перпендикулярны между собой, т.е.
Слайд 18Общее уравнение прямой
Теорема. В прямоугольной системе координат каждая прямая определяется уравнением
первой степени
Ax+By+C=0,
и обратно уравнение Ax+By+C=0 при произвольных коэффициентах A, B и C (A и B не равны нулю одновременно) определяет некоторую прямую.
Ax+By+C=0,
и обратно уравнение Ax+By+C=0 при произвольных коэффициентах A, B и C (A и B не равны нулю одновременно) определяет некоторую прямую.
Слайд 19Общее уравнение прямой
Опр. Линии, определяемые уравнением первой степени, называются линиями первого
порядка.
Слайд 20Общее уравнение прямой
Таким образом, каждая прямая есть линия первого порядка, и,
наоборот каждая линия первого порядка есть прямая.
Слайд 21Общее уравнение прямой
Опр. Уравнение вида Ax+By+C=0 называется общим уравнением прямой (или
полным уравнением прямой).
Слайд 22Неполное уравнение первой степени.
Уравнение прямой «в отрезках»
Рассмотрим три частных случая, когда
уравнение Ax+By+C=0 является «неполным»:
C=0. Уравнение имеет вид Ax+By=0 и определяет прямую, проходящую через начало координат;
C=0. Уравнение имеет вид Ax+By=0 и определяет прямую, проходящую через начало координат;
Слайд 23Неполное уравнение первой степени.
Уравнение прямой «в отрезках»
B=0 (A≠0). Уравнение имеет вид
Ax+C=0 и определяет прямую, параллельную оси Oy
Это уравнение приводится к виду x=a
Где а - есть величина отрезка, который отсекает прямая на оси Ox
Это уравнение приводится к виду x=a
Где а - есть величина отрезка, который отсекает прямая на оси Ox
Слайд 24Неполное уравнение первой степени.
Уравнение прямой «в отрезках»
A =0 (B ≠0). Уравнение
имеет вид Ву+C=0 и определяет прямую, параллельную оси Oх
Это уравнение приводится к виду x=b где b – величина отрезка, который отсекается прямой на оси Oy
Это уравнение приводится к виду x=b где b – величина отрезка, который отсекается прямой на оси Oy
Слайд 25Неполное уравнение первой степени.
Уравнение прямой «в отрезках»
Пусть теперь дано уравнение Ax+By+C=0
при условии, что ни один из коэффициентов A, B, C не равен нулю.
Слайд 28Метод приведения общего уравнения прямой к нормальному виду
Пусть Ax+By+C=0 – общее
уравнение прямой ,
– ее нормальное уравнение
Так как эти равенства определяют одну и туже прямую, то их коэффициенты пропорциональны, т.е. существует такое μ, что уравнение
μAx+μBy+μC=0
Число μ называется нормирующим множителем
– ее нормальное уравнение
Так как эти равенства определяют одну и туже прямую, то их коэффициенты пропорциональны, т.е. существует такое μ, что уравнение
μAx+μBy+μC=0
Число μ называется нормирующим множителем
