- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Экономико-математические методы анализа в управлении промышленным производством: методы линейного программироания презентация
Содержание
- 1. Экономико-математические методы анализа в управлении промышленным производством: методы линейного программироания
- 2. Общая цель любого экономического анализа – выявление
- 3. выявление резервов повышения эффективности производства; обоснование
- 4. линейное программирование нелинейное программирование
- 5. Линейное программирование – это наука о методах
- 6. 6 1) определение оптимального ассортимента продукции, в
- 7. 4) составление оптимального графика отгрузки с учетом
- 8. Линейное программирование широко применяется в сфере военной
- 9. Общей задачей линейного программирования называется задача, которая
- 10. 10 (2)
- 11. 11 Цель построения модели состоит в определении
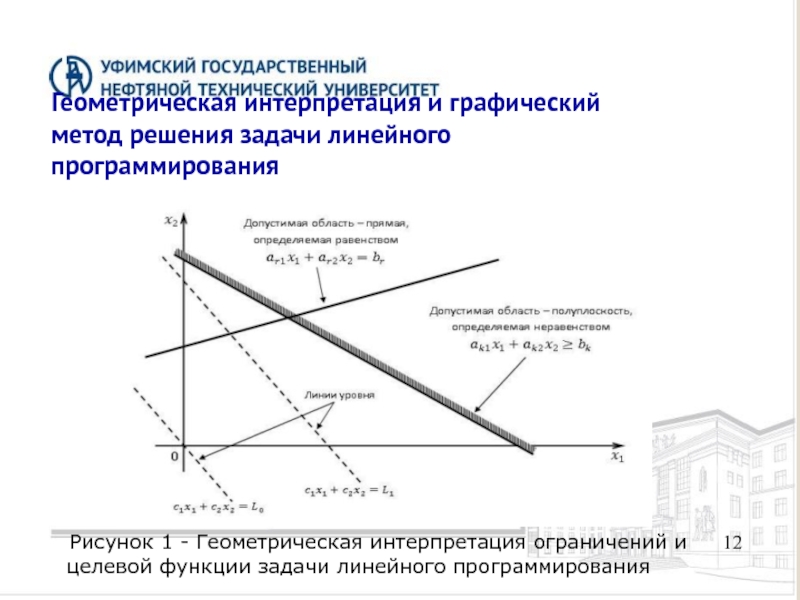
- 12. 12 Геометрическая интерпретация и графический метод решения
- 13. 13 Симплексный метод решения задачи линейного
- 14. 14 ЗАДАЧА 1 Предприятие ООО "Пшеница" предполагает
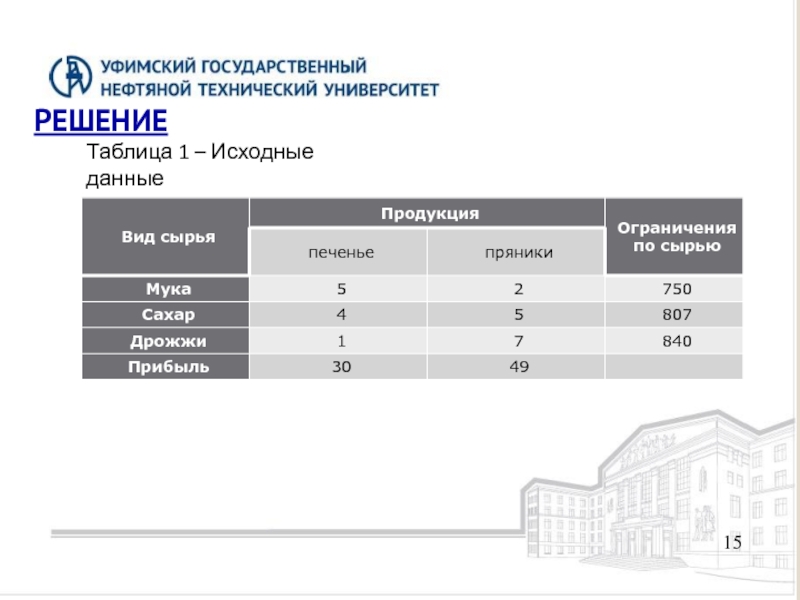
- 15. 15 РЕШЕНИЕ Таблица 1 – Исходные данные
- 16. 16 Пускай X 1 и X 2
- 17. 17 Данная система неравенств считается и концепцией
- 18. 18 После внедрения добавочных переменных приобретаем систему
- 19. 19 Решая задачу, приходим к следующему выводу.
- 20. 20 ЗАДАЧА 2 Рассмотрим симплекс-метод на примере
- 21. 21 РЕШЕНИЕ Приведем ограничения задачи к каноническому
- 22. 22 Дополнительные неотрицательные переменные будут базисными,
- 23. 23 x1 = x2 = 0 (как
- 24. 24 Рассчитаем элементы новой симплексной таблицы (таблица
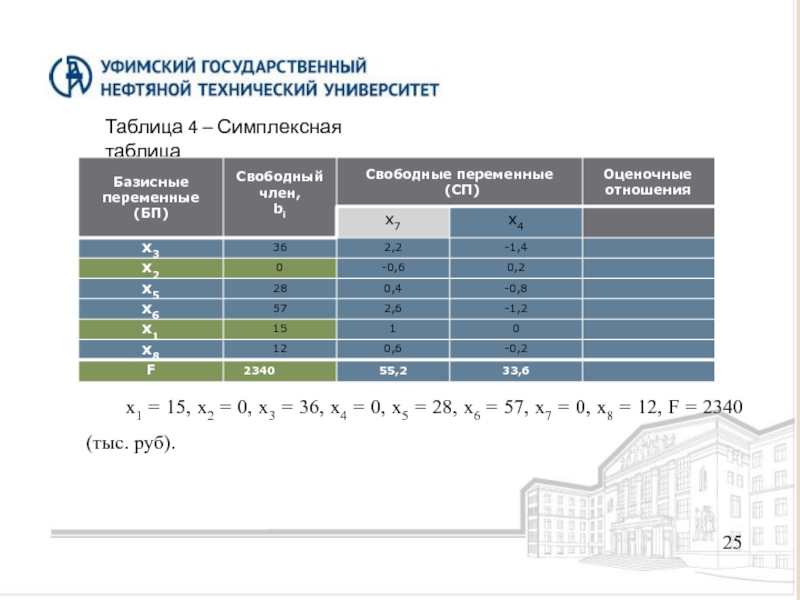
- 25. 25 Таблица 4 – Симплексная таблица x1
- 26. 26 Из решения видно, что сыр «Нежный»
- 27. Спасибо за внимание
Слайд 1ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ АНАЛИЗА В УПРАВЛЕНИИ ПРОМЫШЛЕННЫМ ПРОИЗВОДСТВОМ: МЕТОДЫ ЛИНЕЙНОГО ПРОГРАММИРОАНИЯ
Выполнил: ст.гр.МТП-21-16-01
Руководитель: канд. экон. наук, доц О. А. Александрова
Слайд 2Общая цель любого экономического анализа – выявление и реализация резервов повышения
Задачи экономического анализа:
изучение и объективная оценка показателей, отражающих эффективность функционирования организации, выявление размера и динамики отклонений от базисных значений показателей;
диагностика хозяйственных процессов, установление количественных характеристик действия различных факторов на результативность производства;
2
Цели и задачи экономического анализа производства
Слайд 3выявление резервов повышения эффективности производства;
обоснование принимаемых управленческих решений;
контроль за
установление экономических закономерностей в развитии организации для стратегического прогнозирования и текущего планирования хозяйственной деятельности.
3
Слайд 4 линейное программирование
нелинейное программирование
динамическое программирование
теория игр.
4
Математическое программирование
включает
Слайд 5Линейное программирование – это наука о методах исследования и отыскания наибольших
5
Линейное программирование
Слайд 66
1) определение оптимального ассортимента продукции, в котором каждому ее виду свойственны
2) сведение к минимуму отходов при раскрое материала;
3) определение оптимальных уровней запасов на складе предприятия;
Общие задачи линейного программирования
Слайд 74) составление оптимального графика отгрузки с учетом распределения продукции между производственными
5) определение наилучшего пункта местоположения производства путем оценки затрат на транспортировку между альтернативными местами размещения нового предприятия и местами его снабжения и сбыта готовой продукции;
6) минимизация издержек при распределении рабочих по станкам и рабочим местам
7
Слайд 8Линейное программирование широко применяется в сфере военной деятельности, сельском хозяйстве, промышленности,
8
Слайд 9Общей задачей линейного программирования называется задача, которая состоит в определении max
(1)
9
Общая задача линейного программирования
Слайд 1010
(2)
где cj, aij, bi -заданные действительные числа, (1) - целевая функция,
Слайд 1111
Цель построения модели состоит в определении
уровней (объемов производства) каждого
вида
при которых оптимизируется (максимизируется
или минимизируется) общий результат
производственной деятельности системы
в целом без нарушения ограничений,
накладываемых на использование ресурсов.
Слайд 1212
Геометрическая интерпретация и графический
метод решения задачи линейного
программирования
Рисунок 1 -
Слайд 1313
Симплексный метод решения задачи
линейного программирования
В основе метода лежит идея последовательного
Слайд 1414
ЗАДАЧА 1
Предприятие ООО "Пшеница" предполагает выпускать два вида продукции: печенье и
Слайд 1616
Пускай X 1 и X 2 - количество печенья и пряников,
Слайд 1717
Данная система неравенств считается и концепцией ограничений этой проблемы. Целевая роль
Итак, задача сводится к нахождению максимума функции ограничениях:
Слайд 1818
После внедрения добавочных переменных приобретаем систему уравнений:
Необходимо отыскать такое возможное базисное
Слайд 1919
Решая задачу, приходим к следующему выводу.
Таким образом, для получения наибольшей прибыли,
Слайд 2020
ЗАДАЧА 2
Рассмотрим симплекс-метод на примере решения задачи о производстве сыров. Математическая
Слайд 2121
РЕШЕНИЕ
Приведем ограничения задачи к каноническому виду,
добавив к их левым частям
переменные x3, x4, x5, x6, x7, x8, и запишем расширенную систему:
Слайд 2222
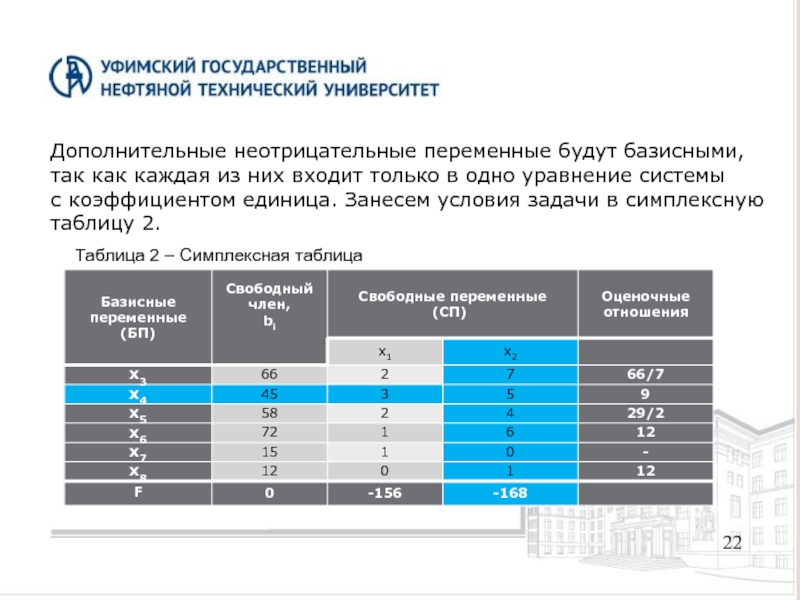
Дополнительные неотрицательные переменные будут базисными,
так как каждая из них входит
с коэффициентом единица. Занесем условия задачи в симплексную
таблицу 2.
Таблица 2 – Симплексная таблица
Слайд 2323
x1 = x2 = 0 (как небазисные переменные)
Дополнительные переменные x3
(F = 0).
Разрешающую строку находим по наименьшему положительному симплексному отношению:
Слайд 2424
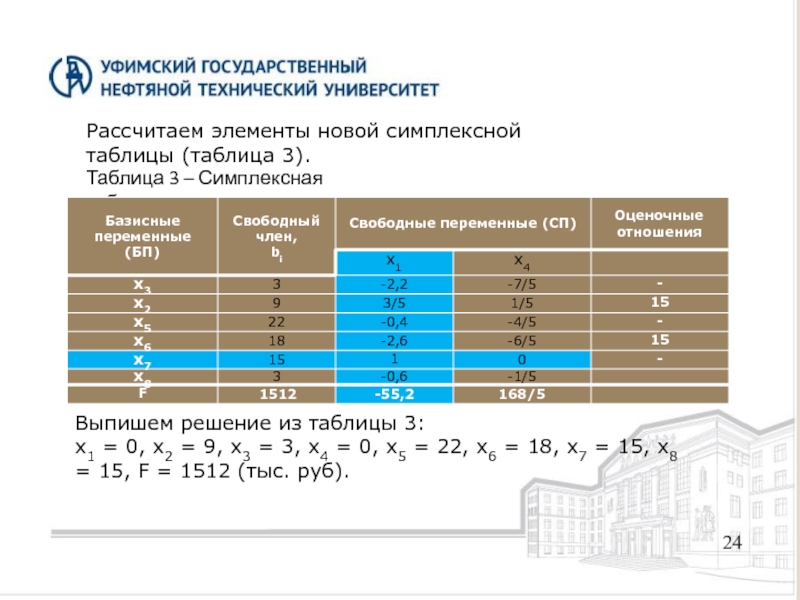
Рассчитаем элементы новой симплексной таблицы (таблица 3).
Таблица 3 – Симплексная таблица
Выпишем
x1 = 0, x2 = 9, x3 = 3, x4 = 0, x5 = 22, x6 = 18, x7 = 15, x8 = 15, F = 1512 (тыс. руб).