обучения для учащихся 11 для подготовки учащихся к решению задач повышенной сложности по теме - «Тригонометрические уравнения и неравенства».
Работа выполнена учителем математики МОУ «Курлекская СОШ» Томского района Томской области
Логуновой Л.В.
Курлек - 2006
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Единичная окружность в тригонометрии презентация
Содержание
- 1. Единичная окружность в тригонометрии
- 2. Зачем нужна единичная окружность? Рис.1 Единичная
- 3. Содержание Урок 1 – «Отображение точек числовой
- 4. Урок 1 Определение Способ задания соответствие
- 5. Определение единичной окружности Окружность радиуса 1 с
- 6. Способ задания соответствия между
- 7. Так как длина окружности вычисляется по
- 8. Смотрите рис.3 2.Каждая точка окружности изображает бесконечное
- 9. Упражнение I.1 Назовите по одному положительному или
- 10. Упражнение I.2 Выберите точки на единичной окружности,
- 11. Урок 2 Способы записи чисел, соответствующих
- 12. Способы записи чисел, соответствующих одной точке единичной
- 13. Упражнение II.1 Выберите все числа, соответствующие указанным
- 14. Вернуться к упражнению к упражнению II.к упражнению II.1 Ошибка
- 15. Вернуться к упражнению II.1
- 16. Вернуться к упражнению II.1
- 17. Вернуться к упражнению II.1
- 18. К упражнению II.2 Вернуться к упражнению II.1
- 19. Упражнение II.2 Выберите все числа, соответствующие указанным
- 20. Правильно! Вернуться к упражнению II.2 На содержание
- 21. Ошибка! Вернуться к упражнению II.2
- 22. Урок 3 Отбор чисел (Метод «лепестков»)
- 23. Отбор корней (Метод «лепестков») Решение многих
- 24. Решение Теперь перенесем лепестки в нужные места
- 25. Пример 2 Переписать данное условие так, чтобы
- 26. Пример 3 Запишите без повторений значения х,
- 27. Пример 4 Запишите без повторений значения х,
- 28. Переписать данное условие так, чтобы в них
- 29. Правильно! Упражнение I,1 Упражнение I,2
- 30. Ошибка! Вернуться к упражнению I,2 Вернуться к упражнению I,1
- 31. Урок 4 Запись промежутков Упражнения На содержание
- 32. Запись промежутков Запиши все числа,
- 33. Упражнения Поставь в соответствие числовому
- 34. Урок 5 Решение тригонометрических неравенств (примеры) Задание На содержание
- 35. Урок 5 Пример Решить неравенство:
- 36. Урок 5 Самостоятельная работа Реши неравенство: Ответ Ответ Ответ
- 37. Урок 5 Ответ: К самостоятельной работе
- 38. Урок 5 Ответ: К самостоятельной работе
- 39. Урок 5 Ответ: К самостоятельной работе На итог
- 40. Подведем итог Теперь ты можешь приступать к
- 41. Содержание Урок 1 – «Отображение точек числовой
- 42. Литература и другие ресурсы для самостоятельной работы
Зачем нужна единичная окружность? Рис.1 Единичная окружность необходима при изучении тригонометрических функций и построении их графиков, часто используется в решении тригонометрических уравнений и неравенств при отборе корней. Цель: повторить, как
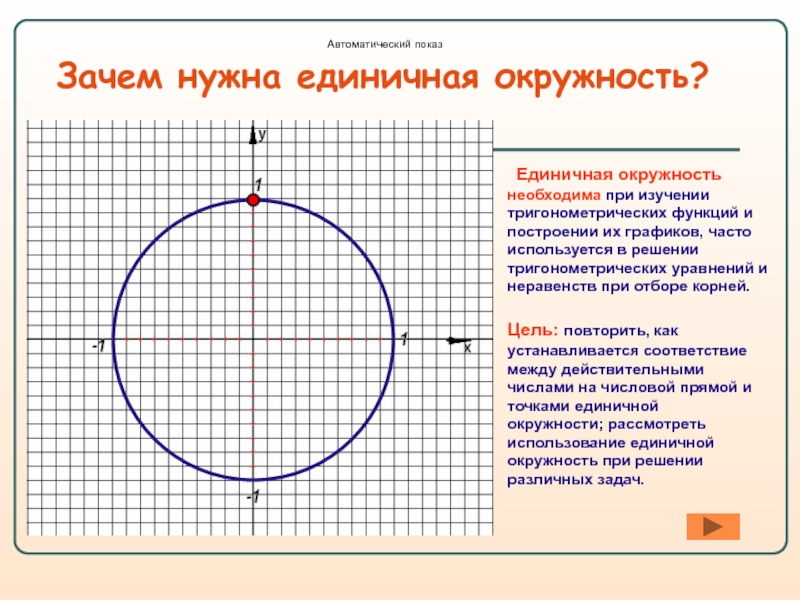
Слайд 2Зачем нужна единичная окружность?
Рис.1
Единичная окружность необходима при изучении тригонометрических функций
и построении их графиков, часто используется в решении тригонометрических уравнений и неравенств при отборе корней.
Цель: повторить, как устанавливается соответствие между действительными числами на числовой прямой и точками единичной окружности; рассмотреть использование единичной окружность при решении различных задач.
Автоматический показ
Слайд 3Содержание
Урок 1 – «Отображение точек числовой прямой на точки единичной окружности»
Урок
2 – «Способ записи координаты точки единичной окружности»
Урок 3 – «Метод лепестков»
Урок 4 – «Числовые промежутки на единичной окружности»
Урок 5 – «Решение тригонометрических неравенств»
Автоматический показ
Итог
Слайд 4Урок 1
Определение
Способ задания соответствие между множеством действительных чисел и точками единичной
окружности (криволинейная система координат)
Упражнения (тесты)
Упражнения (тесты)
На содержание
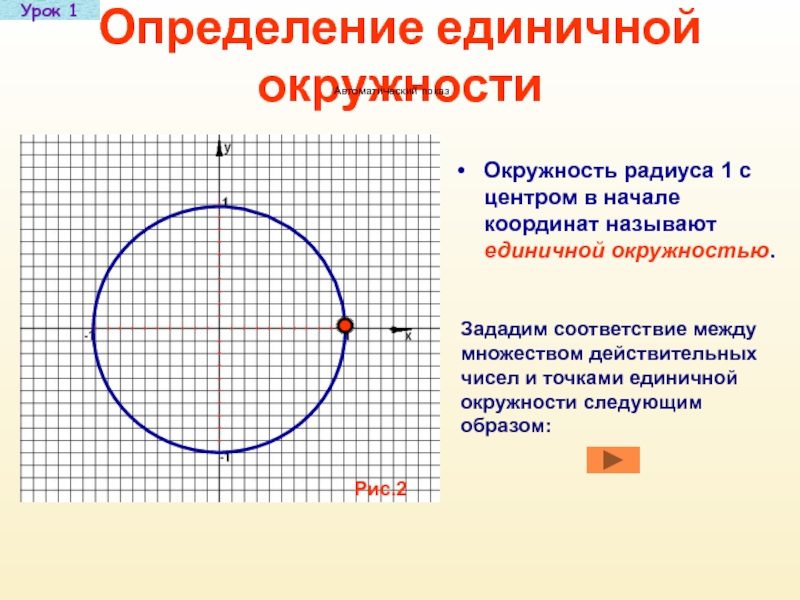
Слайд 5Определение единичной окружности
Окружность радиуса 1 с центром в начале координат называют
единичной окружностью.
Зададим соответствие между множеством действительных чисел и точками единичной окружности следующим образом:
Рис.2
Автоматический показ
Урок 1
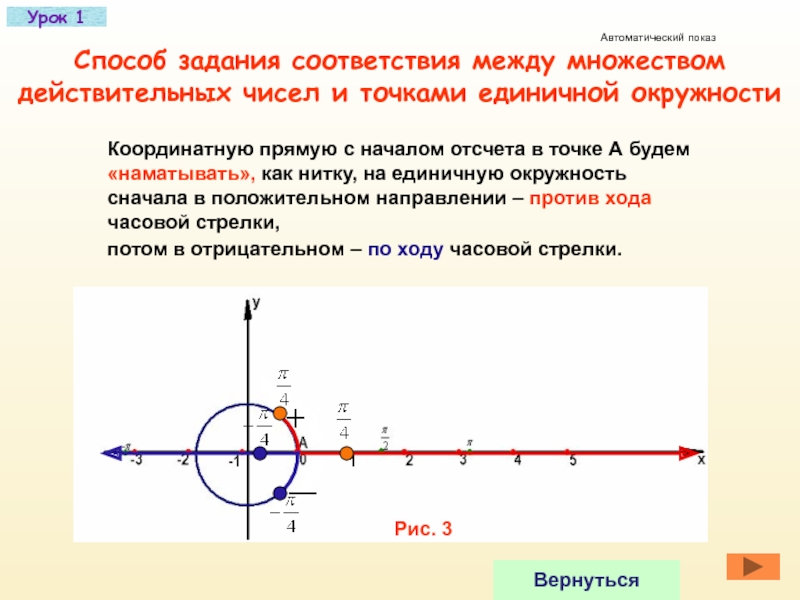
Слайд 6 Способ задания соответствия между множеством действительных чисел и точками единичной окружности
Координатную прямую с началом отсчета в точке А будем «наматывать», как нитку, на единичную окружность сначала в положительном направлении – против хода часовой стрелки,
Рис. 3
Вернуться
потом в отрицательном – по ходу часовой стрелки.
Автоматический показ
Урок 1
Слайд 7
Так как длина окружности вычисляется по формуле
, то можно получить изображение таких чисел на окружности как:
Рис.4
Урок 1
Слайд 8Смотрите рис.3
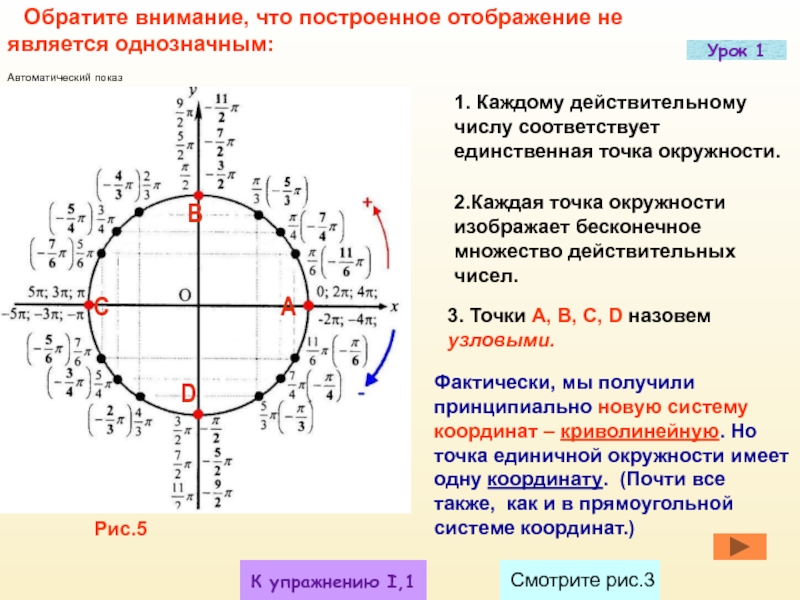
2.Каждая точка окружности изображает бесконечное множество действительных чисел.
3. Точки A,
B, C, D назовем узловыми.
1. Каждому действительному числу соответствует единственная точка окружности.
К упражнению I,1
А
В
С
D
Рис.5
Автоматический показ
Урок 1
Обратите внимание, что построенное отображение не является однозначным:
Фактически, мы получили принципиально новую систему координат – криволинейную. Но точка единичной окружности имеет одну координату. (Почти все также, как и в прямоугольной системе координат.)
Слайд 9Упражнение I.1
Назовите по одному положительному или отрицательному числу, которые не записаны
на модели единичной окружности, но соответствуют каждой из узловых точек.
Выбери ответ:
Рис.6
На упражнение I.2
Урок 1
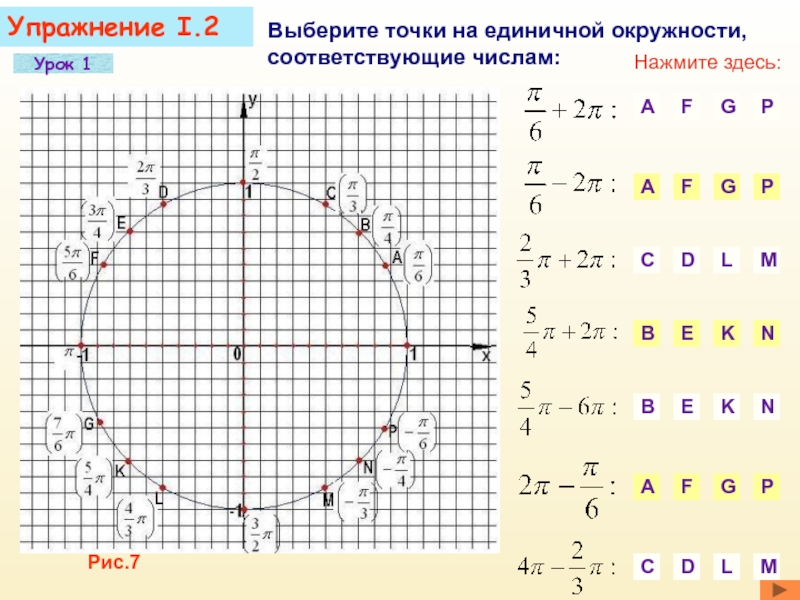
Слайд 10Упражнение I.2
Выберите точки на единичной окружности, соответствующие числам:
A
A
F
G
P
F
G
P
C
D
L
M
B
E
K
N
A
F
G
P
B
E
K
N
C
D
L
M
Рис.7
Нажмите здесь:
Урок 1
Слайд 11Урок 2
Способы записи чисел, соответствующих одной точке единичной окружности
Упражнения:
II.1
II.2
На содержание
Слайд 12Способы записи чисел, соответствующих одной точке единичной окружности
К упражнению II.1
Автоматический показ
Урок 2
Слайд 13Упражнение II.1
Выберите все числа, соответствующие указанным точкам единичной окружности
На содержание
На упражнение
II.2
Урок 2
Слайд 19Упражнение II.2
Выберите все числа, соответствующие указанным точкам единичной окружности
На содержание
На урок
3
Урок 2
Слайд 23Отбор корней
(Метод «лепестков»)
Решение многих тригонометрических уравнений приводит к совокупности или
системе их корней. Для грамотной записи ответа, требующей, в частности, исключения повторяющихся чисел, мы используем единичную окружность.
Каждой серии чисел присваивается лепесток определенного цвета:
Пример 1
Переписать данное условие так, чтобы в них не было повторений.
Автоматический показ
Урок 3
Слайд 24Решение
Теперь перенесем лепестки в нужные места тригонометрической окружности
Остается только
записать числа, соответствующие точкам, около каждой из которых расположен хоть один лепесток
Ответ:
Автоматический показ
Урок 3
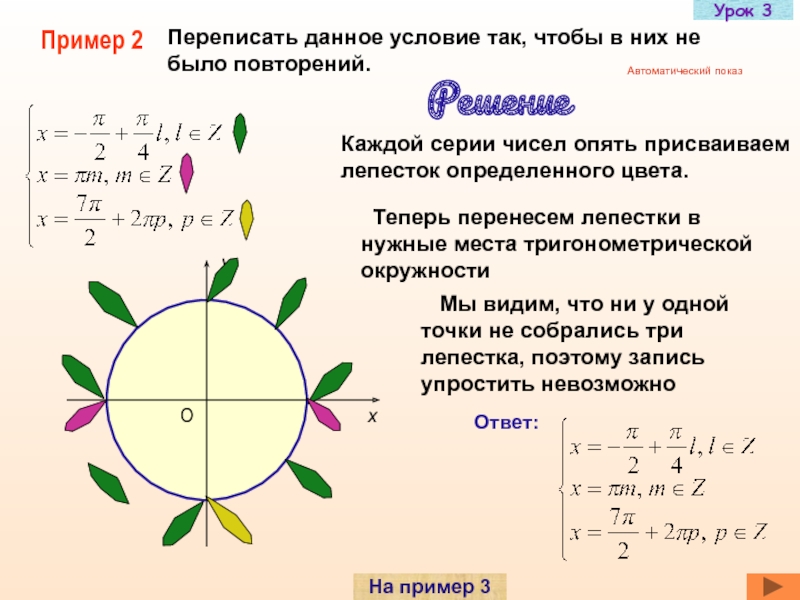
Слайд 25Пример 2
Переписать данное условие так, чтобы в них не было повторений.
Решение
Каждой
серии чисел опять присваиваем лепесток определенного цвета.
Теперь перенесем лепестки в нужные места тригонометрической окружности
Мы видим, что ни у одной точки не собрались три лепестка, поэтому запись упростить невозможно
Ответ:
На пример 3
Автоматический показ
Урок 3
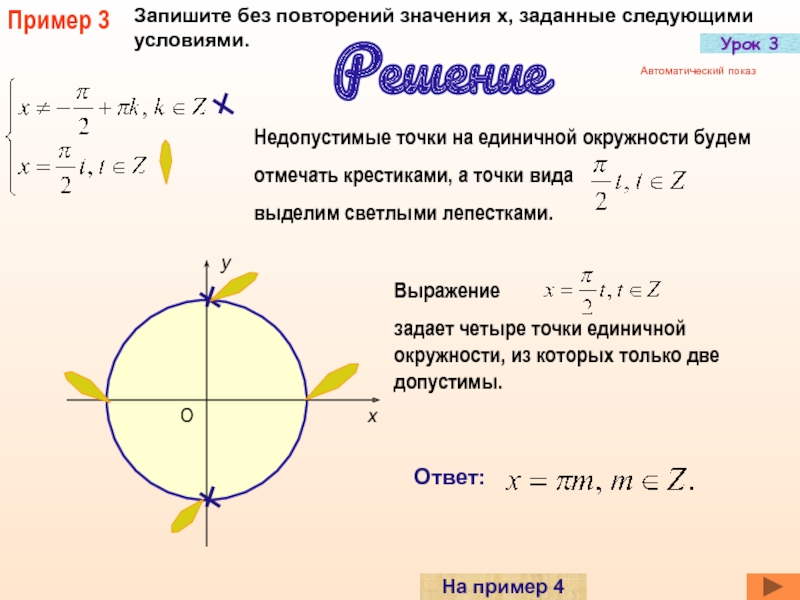
Слайд 26Пример 3
Запишите без повторений значения х, заданные следующими условиями.
Решение
Ответ:
На пример 4
Автоматический
показ
Урок 3
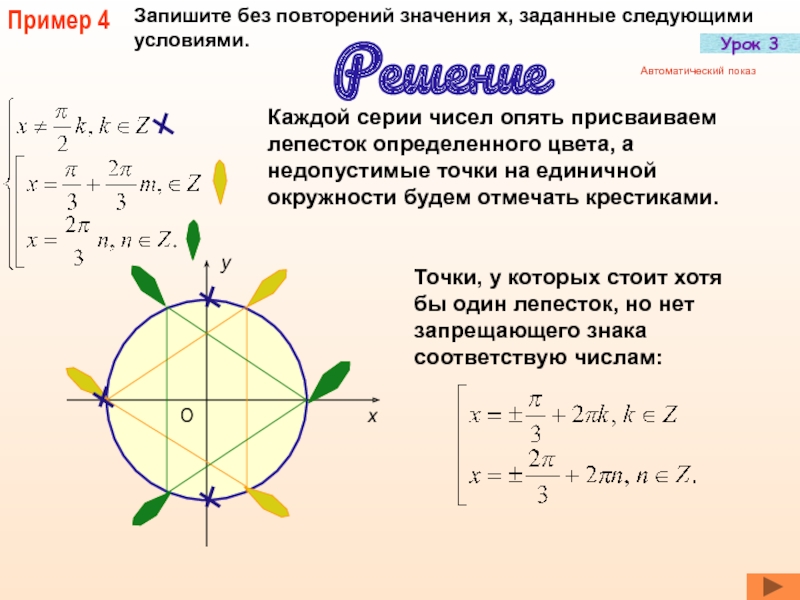
Слайд 27Пример 4
Запишите без повторений значения х, заданные следующими условиями.
Решение
Каждой серии чисел
опять присваиваем лепесток определенного цвета, а недопустимые точки на единичной окружности будем отмечать крестиками.
Точки, у которых стоит хотя бы один лепесток, но нет запрещающего знака соответствую числам:
Автоматический показ
Урок 3
Слайд 28Переписать данное условие так, чтобы в них не было повторений в
заданиях 1 и 2.
Выбери ответ:
Выбери ответ:
Упражнения
3)Выбрать наибольшее отрицательное число.
4)Переписать данное условие так, чтобы в них не было повторений
Выбери ответ:
Выбери ответ:
Урок 3
На урок 4
Слайд 32Запись промежутков
Запиши все числа, соответствующие точкам выделенной дуги (или
двух дуг) на рисунке:
Решение
Около одного из концов дуги записываем одно из чисел, соответствующих этой точке.
Рисуем стрелку, направленную к другому концу отмеченной дуги.
Стрелка снабжается знаком «+», если движение направлено против хода часовой стрелки, и знаком «-» минус, если оно идет по ходу часовой стрелки.
Записываем соответствующее число около второго конца дуги.
Записываем ответ с учетом, что каждой точке единичной окружности соответствует бесконечное множество действительных чисел.
Пример
Ответ:
Автоматический показ
Урок 4
Слайд 33Упражнения
Поставь в соответствие числовому промежутку номер рисунка
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
Урок 4
На урок
5
Слайд 35Урок 5
Пример
Решить неравенство:
Решение
Рассмотрим единичную окружность:
1)Проведем прямую
2)Заштрихуем
точки на оси y, для которых
3)Выделим точки единичной окружности, которые им соответствуют.
M
N
4)Вдоль заштрихованной дуги МN проведем стрелку в положительном направлении (против часовой стрелки).
5)Роль начальной точки играет точка М, а конечной точка N.
6)Ядро решения неравенства -
7)Точкам M и N «присваиваем имена» -
8)»Ядро» ответа -
9)Ответ:
Автоматический показ
Слайд 40Подведем итог
Теперь ты можешь приступать к решению заданий повышенной сложности по
тригонометрии, то есть к решению тригонометрических уравнений и задач. Ведь ты теперь знаешь и умеешь
Смотри
Слайд 41Содержание
Урок 1 – «Отображение точек числовой прямой на точки единичной окружности»
Урок
2 – «Способ записи координаты точки единичной окружности»
Урок 3 – «Метод лепестков»
Урок 4 – «Числовые промежутки на единичной окружности»
Урок 5 – «Решение тригонометрических неравенств»
Смотри список литературы и других ресурсов
Слайд 42Литература и другие ресурсы для самостоятельной работы
Практикум по элементарной математике. Тригонометрия.
Авторы – В.Н. Литвиненко, А.Г. Мордкович, Москва, «Вербум – М», 2000.
Лев Великович "Лоцман абитуриента в океане математики" http://www.trizway.com/show.php?id=63&pg=1#a1
(Подключись к Интернету, скопируй эту ссылку в адресную строку в обозревателе и нажми «Enter» ).
Сайт элементарной математики Дмитрия Гущина
http://mathnet.spb.ru/
(Подключись к Интернету, скопируй эту ссылку в адресную строку в обозревателе и нажми «Enter» ).
Лев Великович "Лоцман абитуриента в океане математики" http://www.trizway.com/show.php?id=63&pg=1#a1
(Подключись к Интернету, скопируй эту ссылку в адресную строку в обозревателе и нажми «Enter» ).
Сайт элементарной математики Дмитрия Гущина
http://mathnet.spb.ru/
(Подключись к Интернету, скопируй эту ссылку в адресную строку в обозревателе и нажми «Enter» ).
Не упускай своих возможностей!
Твой учитель!
На содержание
