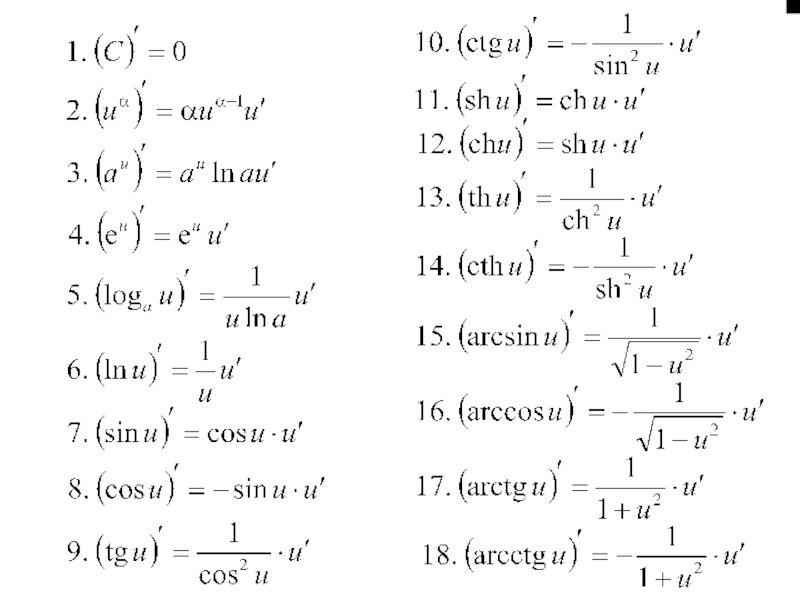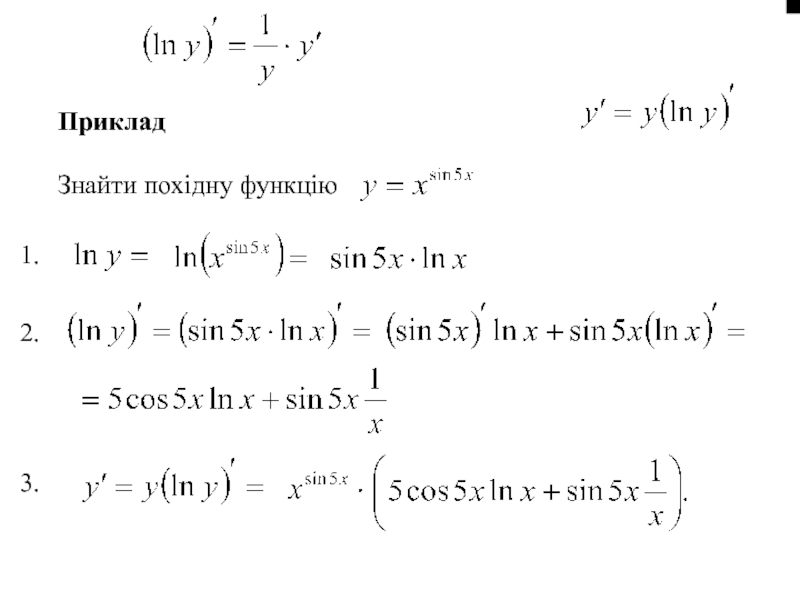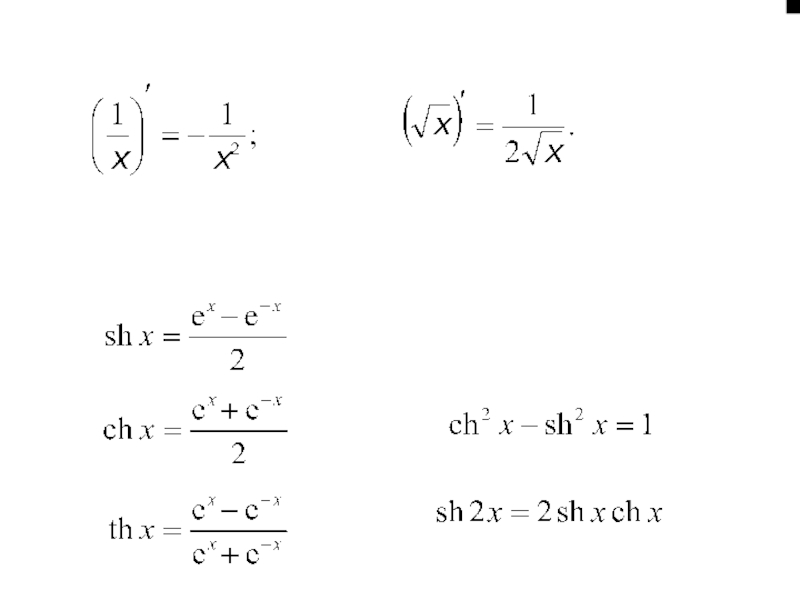- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дійсні числа презентация
Содержание
- 2. §1. Дійсні числа 1.1. Множини. Логічні символи ∅ Глава 4 Вступ до математичного аналізу
- 3. 1.1. Множини. Логічні символи
- 4. 1.1. Множини. Логічні символи
- 5. 1.1. Множини. Логічні символи
- 6. 1.1. Множини. Логічні символи
- 7. 1.2. Множина дійсних чисел ℕ ℤ ℚ ℝ
- 8. 1.3. Числові проміжки. Окіл точки Околом
- 9. 1.4. Модуль (абсолютна величина) дійсного числа
- 10. §2. Функції
- 11. Головні види відповідності між елементами двох множин
- 12. Головні види відповідності між елементами двох множин
- 13. Головні види відповідності між елементами двох множин
- 14. Відношення Поняття функції
- 15. Функція Поняття функції
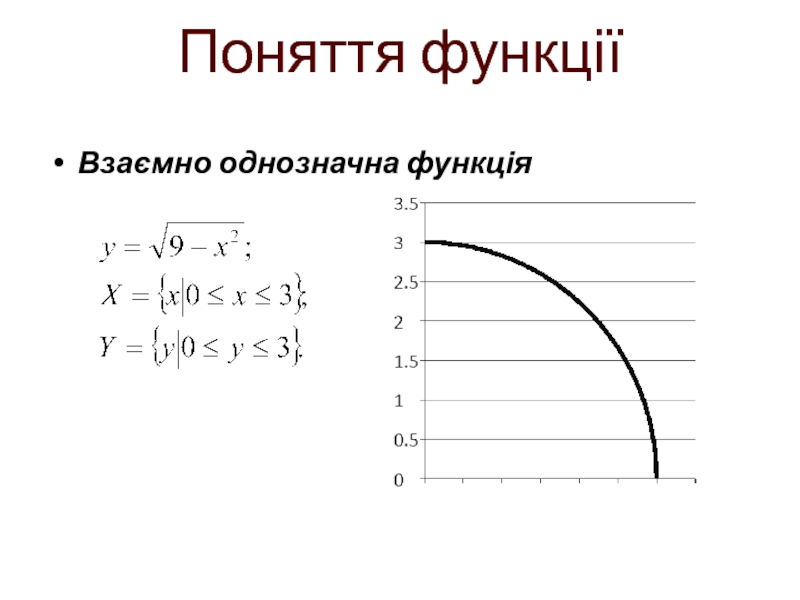
- 16. Взаємно однозначна функція Поняття функції
- 17. Поняття функції Термін «функція» вперше ввів Г.
- 18. Поняття функції Озн. Числовою функцією з областю
- 19. Поняття функції
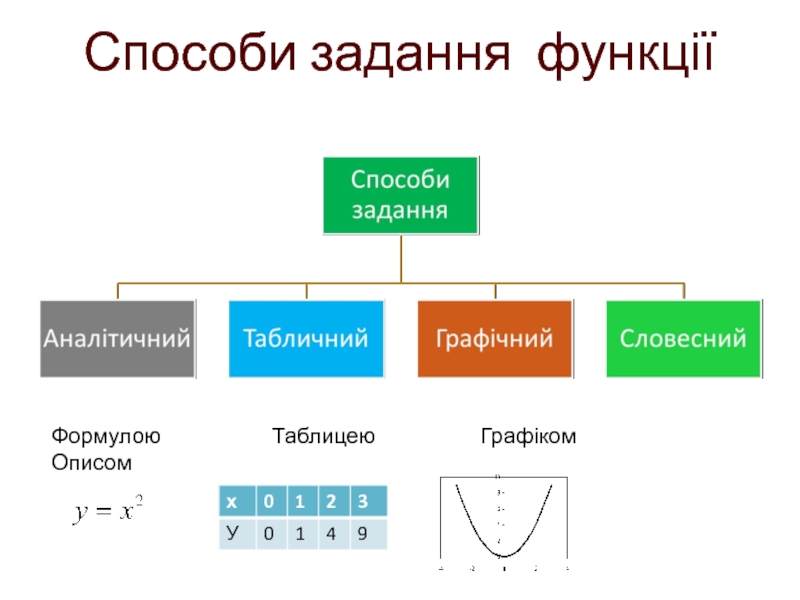
- 20. Способи задання функції Формулою
- 21. Способи задання функції
- 22. Властивості функцій Озн. Функцію y = f(x),
- 23. Властивості функцій Озн. Функція y = f(x)
- 24. Властивості функцій Озн. Функція y = f(x)
- 25. Властивості функцій Озн. Функція y = f(x),
- 26. Властивості функцій Озн. Під неявним заданням функції
- 27. Властивості функцій Озн. Функція
- 28. Властивості функцій Озн. Задання функціональної залежності між
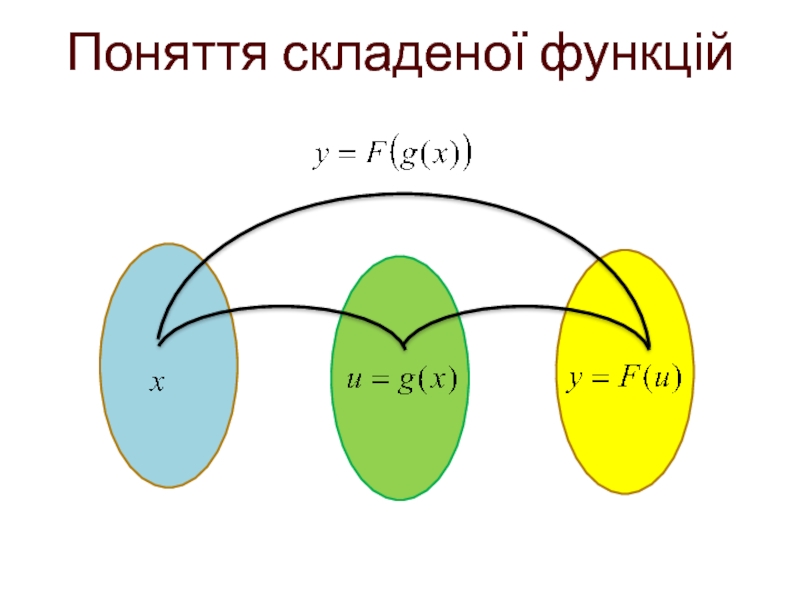
- 29. Поняття складеної функцій
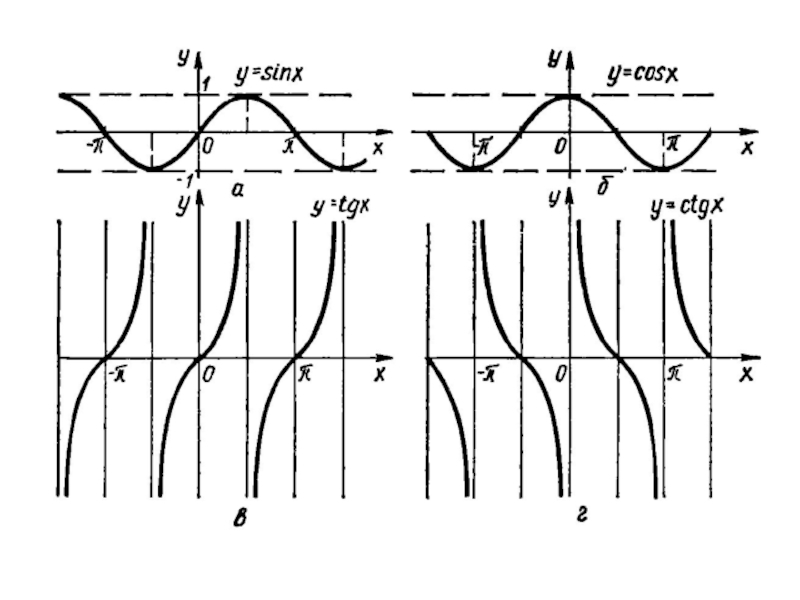
- 30. Елементарні функції Озн. Основними елементарними функціями називаються
- 36. §3. Границя функції 3.1. Числова послідовність
- 37. Якщо кожному натуральному числу п ∈
- 38. Число х0 називається границею послідовності {хn},
- 39. 3.2. Границя числової послідовності. Єдиність границі
- 40. Число А називають границею функції у
- 41. Число А називають границею функції в точці
- 44. Приклад Довести, що
- 45. Приклад Довести, що
- 46. Функцію f (х), задану на всій числовій
- 47. Функцію f (х), задану на всій числовій
- 48. 3.7. Основні теореми про границі Теорема
- 49. Приклад Обчислити
- 50. Приклад Обчислити
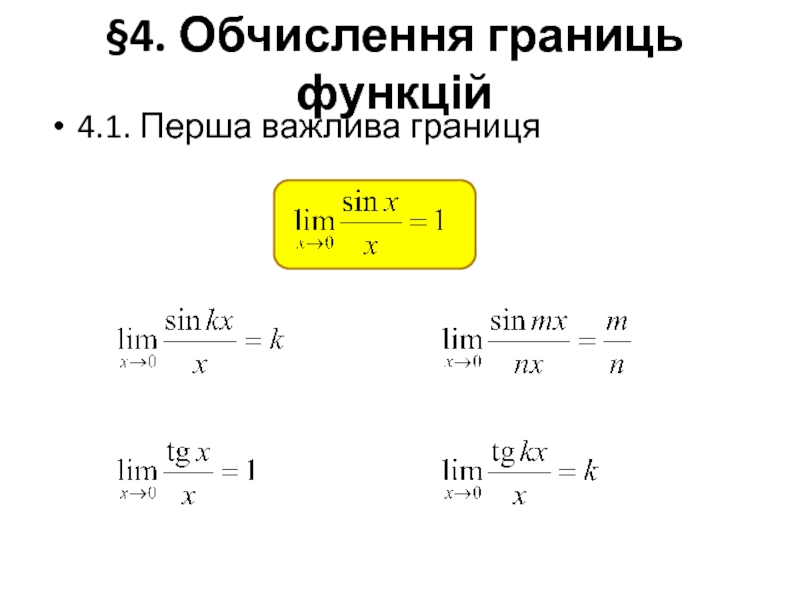
- 52. §4. Обчислення границь функцій 4.1. Перша важлива границя
- 53. Приклад
- 54. 4.3. Друга важлива границя
- 55. Приклад
- 57. Приклад
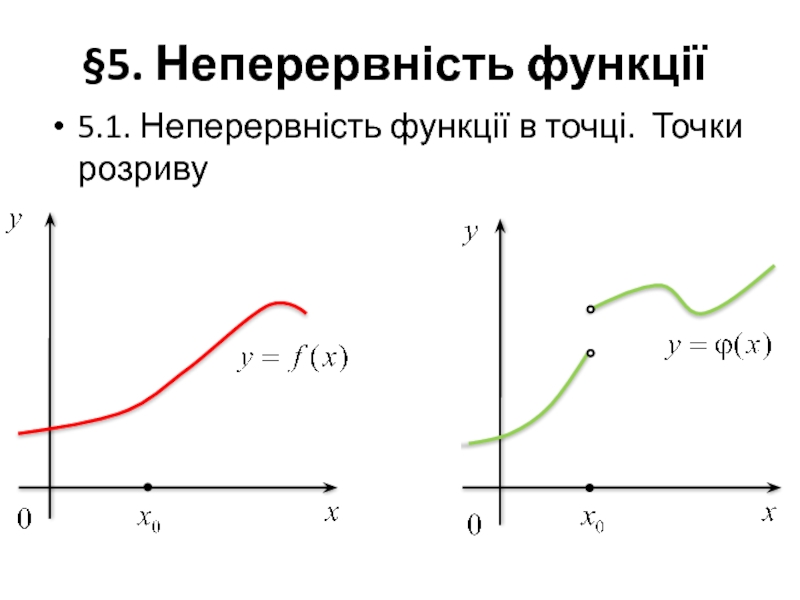
- 58. §5. Неперервність функції 5.1. Неперервність функції в
- 59. Озн. Функція f(х) називається неперервною в
- 61. (26)
- 62. причому не всі числа
- 63. то розрив в точці х0 називають
- 64. Озн. Якщо хоча б одна
- 65. Теорема. Якщо функції f(х) і φ(х)
- 66. Озн. Якщо функція неперервна в кожній
- 67. Теорема. (друга теорема Больцано-Коші). Нехай функція
- 68. Теорема. (Вейєрштрасса). Якщо функція f (х)
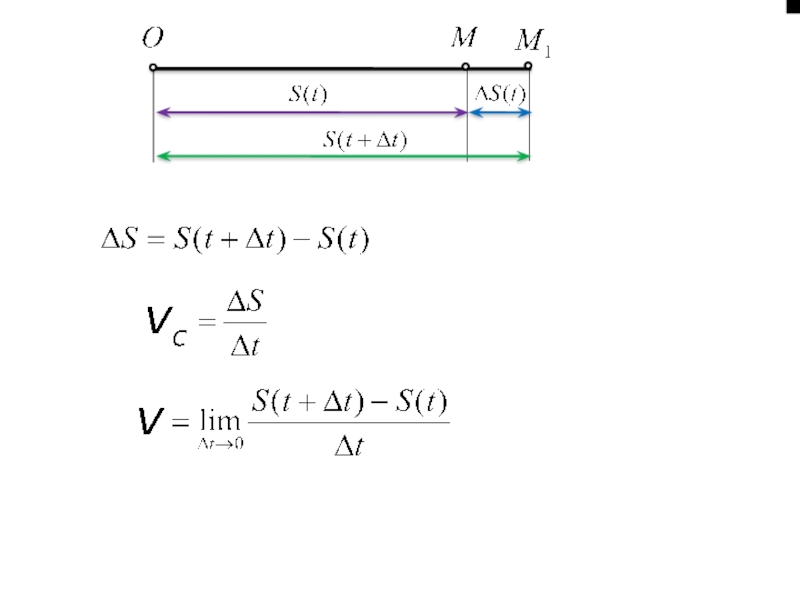
- 69. §1. Похідна 1.1. Задачі, які приводять до
- 71. 1.2. Означення похідної. Механічний, фізичний та
- 72. Приклад Знайти похідну функцію
- 74. Швидкість в даний момент часу — це
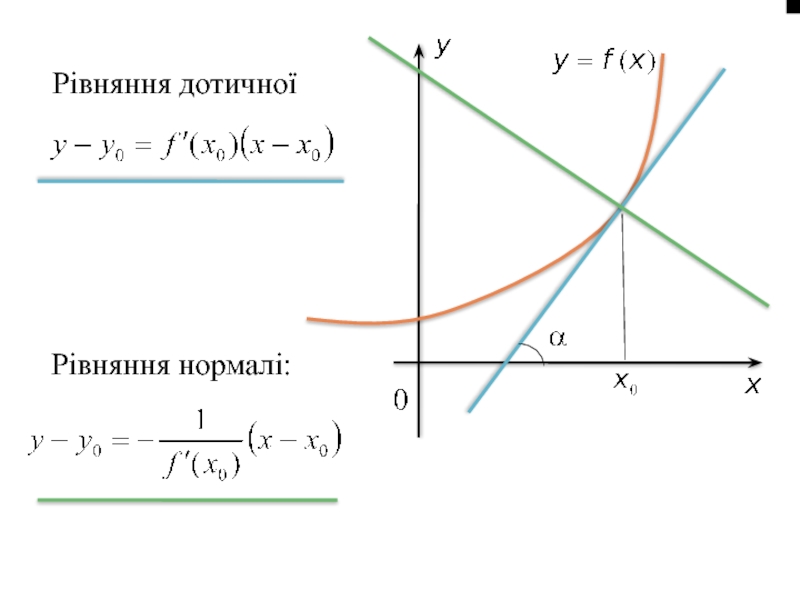
- 75. Рівняння дотичної Рівняння нормалі:
- 76. 1.4. Односторонні похідні. Неперервність і диференційовність Права похідна Ліва похідна
- 77. Озн. Функція f (х) називається диференційовною
- 78. §2. Диференціювання функцій
- 80. Приклад Знайти похідну функцію 1. 2. 3.
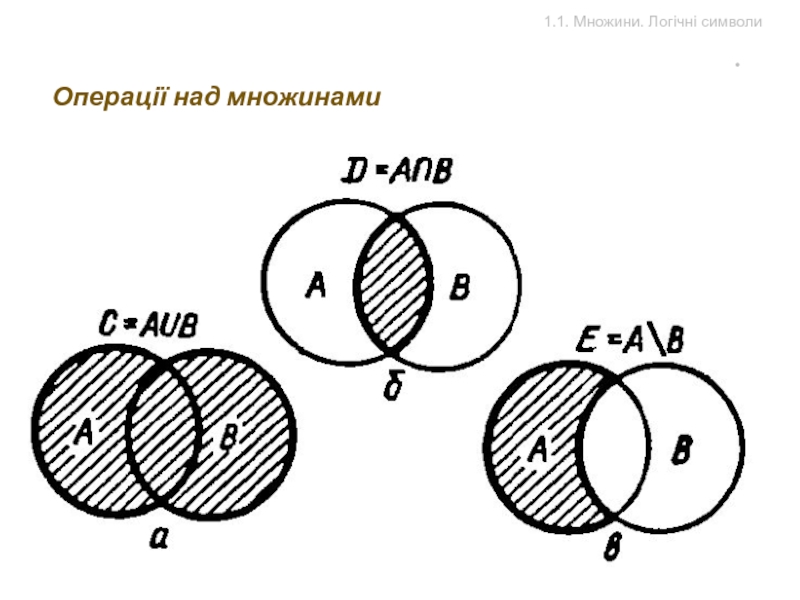
Слайд 3
1.1. Множини. Логічні символи
Операції над множинами
Множину С, яка
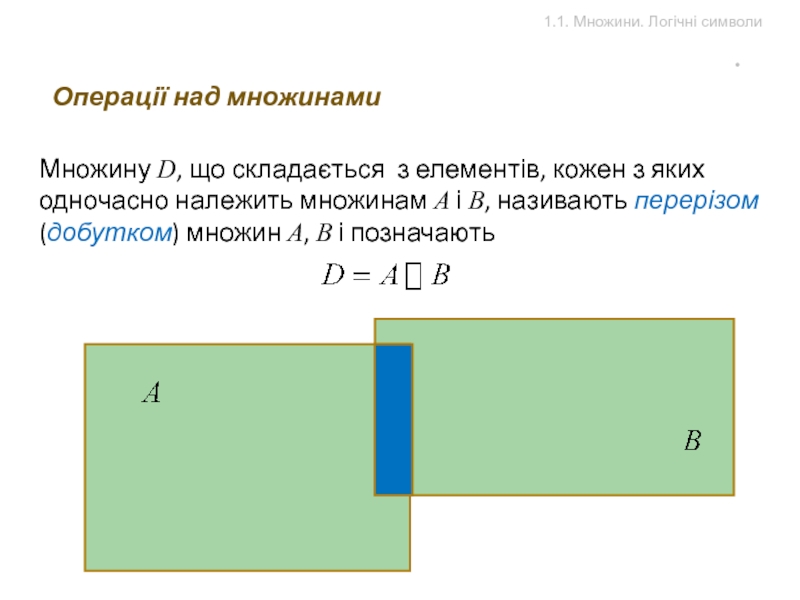
Слайд 4
1.1. Множини. Логічні символи
Операції над множинами
Множину D, що
Слайд 5
1.1. Множини. Логічні символи
Операції над множинами
Множину Е, що
Слайд 81.3. Числові проміжки. Окіл точки
Околом точки x0 називають будь-який інтервал (α,
Інтервал (x0−ε; x0+ε) називають ε −околом точки x0.
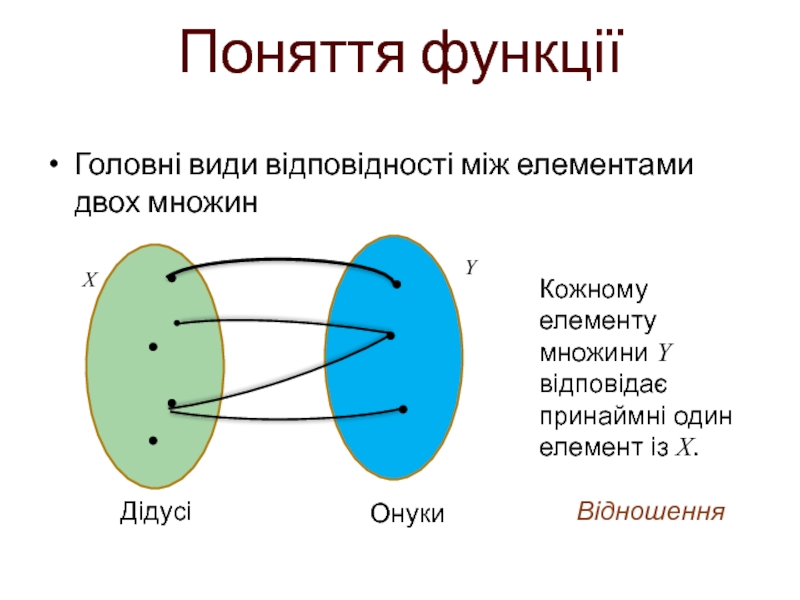
Слайд 11Головні види відповідності між елементами двох множин
Поняття функції
X
Y
Сюр’єкція
Кожному елементу множини Y
Дідусі
Онуки
Відношення
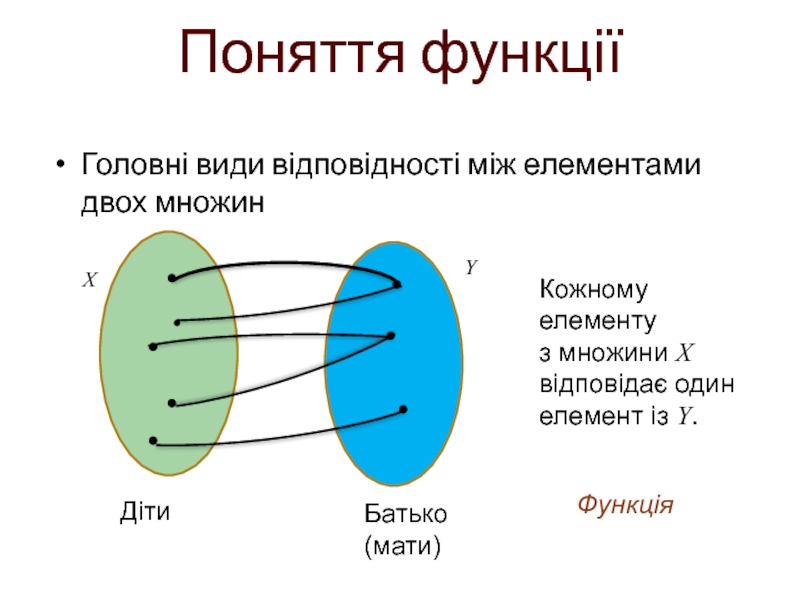
Слайд 12Головні види відповідності між елементами двох множин
Поняття функції
X
Y
Ін’єкція
Кожному елементу
з множини
Діти
Батько (мати)
Функція
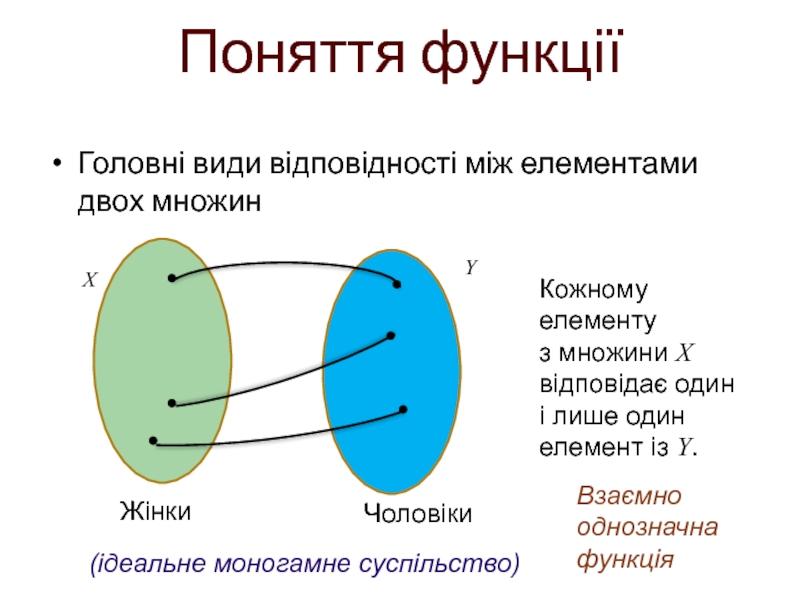
Слайд 13Головні види відповідності між елементами двох множин
Поняття функції
X
Y
Бієкція
Кожному елементу
з множини
Жінки
Чоловіки
Взаємно однозначна функція
(ідеальне моногамне суспільство)
Слайд 17Поняття функції
Термін «функція» вперше ввів Г. Лейбніц.
Озн. Функцією називається відповідність, при
D – область визначення функції (позн. D(f));
Е – область значень функції (позн. E(f)).
Якщо D(f) і E(f) – числові множини, то функція називається числовою.
Слайд 18Поняття функції
Озн. Числовою функцією з областю визначення D називається відповідність, при
Озн. (М. Лобачевського і Л.Діріхле) Якщо кожному числу х з деякої числової множини Х за певним правилом поставлене у відповідність єдине число y, то кажуть, що у є функцією від х.
Слайд 22Властивості функцій
Озн. Функцію y = f(x), визначену на множині Х, називають
Слайд 23Властивості функцій
Озн. Функція y = f(x) називається
монотонно зростаючою,
строго зростаючою,
монотонно спадною,
строго
якщо для кожної пари виконується нерівність:
f(x1) ≤ f(x2).
f(x1) < f(x2).
f(x1) ≥ f(x2).
f(x1) > f(x2).
Слайд 24Властивості функцій
Озн. Функція y = f(x) називається
парною,
непарною,
загального вигляду (ні парна,
якщо для кожного виконується: f(–x) = f(x).
f(–x) = – f(x).
не виконується жодна умова.
(область визначення симетрична відносно точки 0)!
Слайд 25Властивості функцій
Озн. Функція y = f(x), визначена на всій числовій прямій,
Озн. Функція y = f(x), визначена множині Х, називається періодичною на цій множині, якщо існує таке число Т ≠ 0, що х + Т ∈ Х і f(x + Т) = f(x).
Слайд 26Властивості функцій
Озн. Під неявним заданням функції розуміють задання функції у вигляді
Слайд 27Властивості функцій
Озн. Функція
1) областю визначення функції ϕ є множина значень функції f;
2) множина значень функції ϕ є область визначення функції f;
3) кожному значенню змінної y ∈ Y відповідає єдине значення змінної x∈ X.
Слайд 28Властивості функцій
Озн. Задання функціональної залежності між х і y у
називають параметричним заданням функцій.
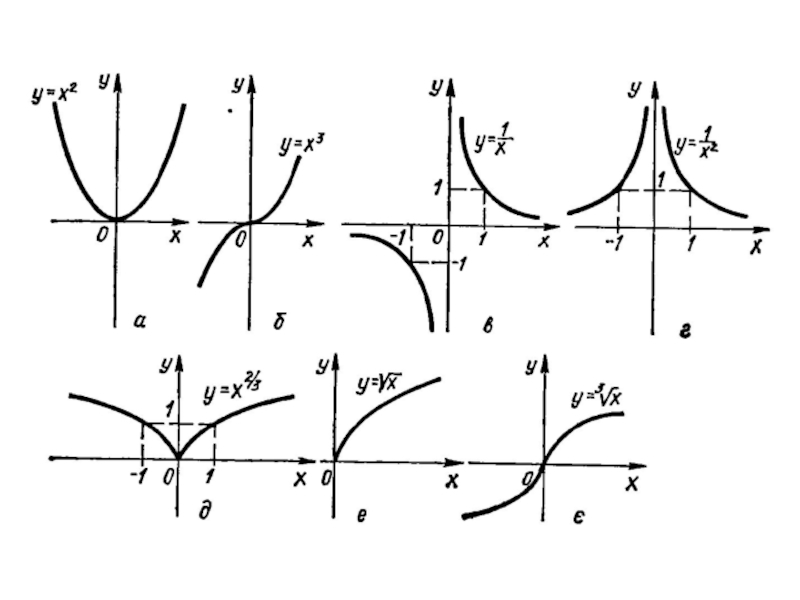
Слайд 30Елементарні функції
Озн. Основними елементарними функціями називаються такі:
1. Лінійна функція
2. Степенева функція
3.
4. Логарифмічна функція
5. Тригонометричні функції
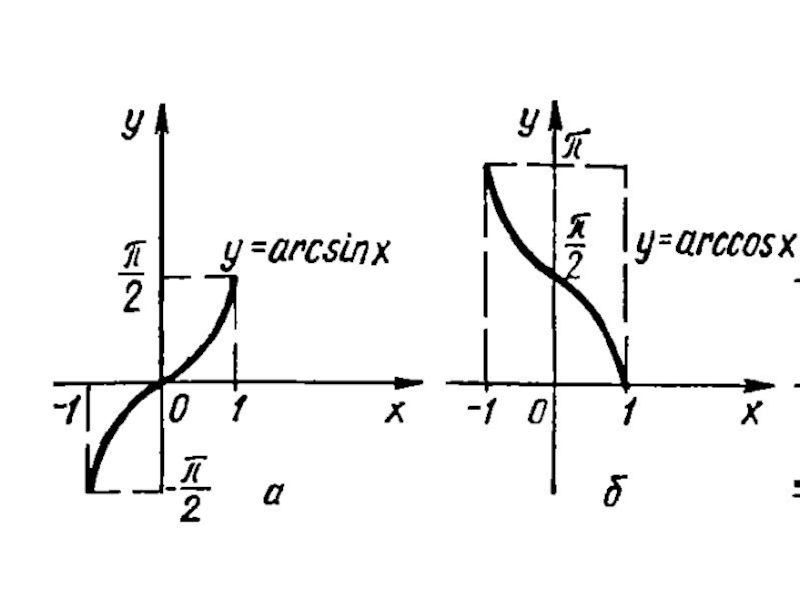
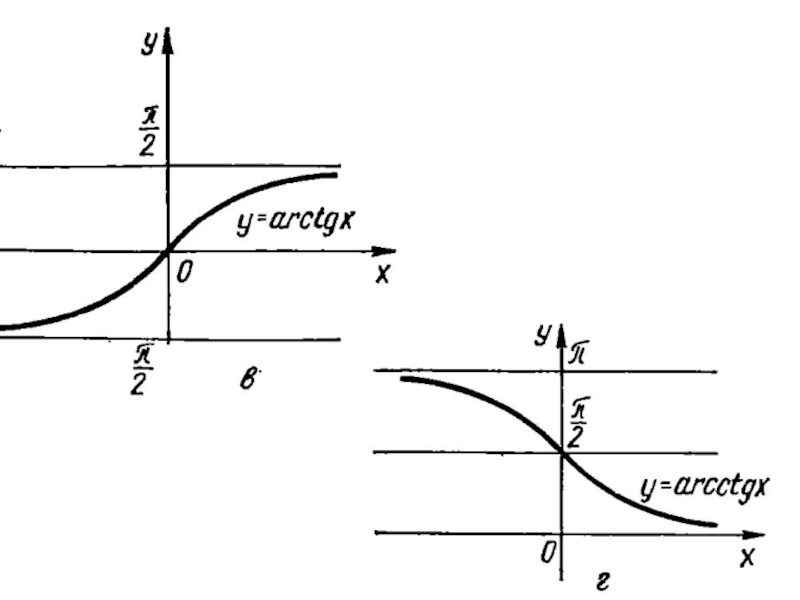
6. Обернені тригонометричні функції
інші.
(Гіперболічні функції )
Слайд 37
Якщо кожному натуральному числу п ∈ ℕ
за певним правилом ставиться
називають числовою послідовністю (або коротко послідовністю) і позначають символом {хn}.
3.1. Числова послідовність
Слайд 38
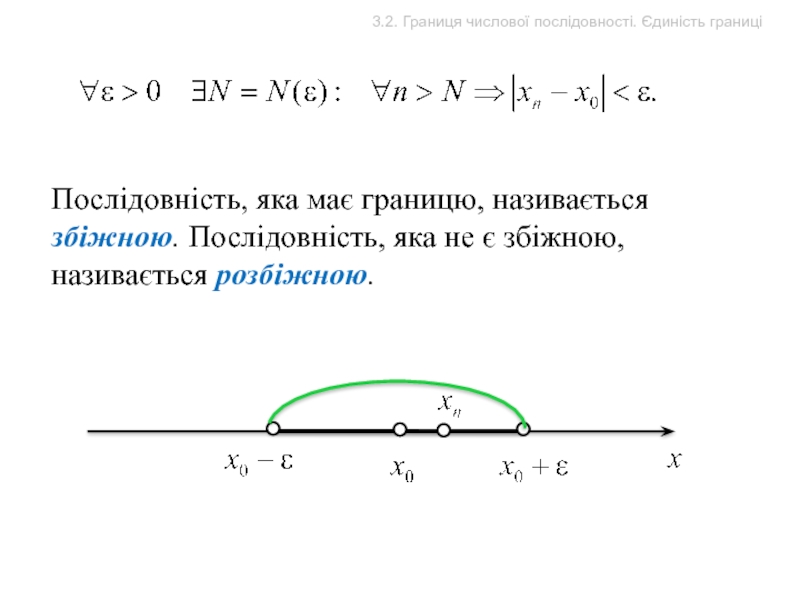
Число х0 називається границею послідовності {хn},
якщо
3.2. Границя числової послідовності. Єдиність границі
Слайд 39
3.2. Границя числової послідовності. Єдиність границі
Послідовність, яка має границю, називається збіжною.
Слайд 40
Число А називають границею функції у = f (х) в точці
3.4. Границя функції в точці
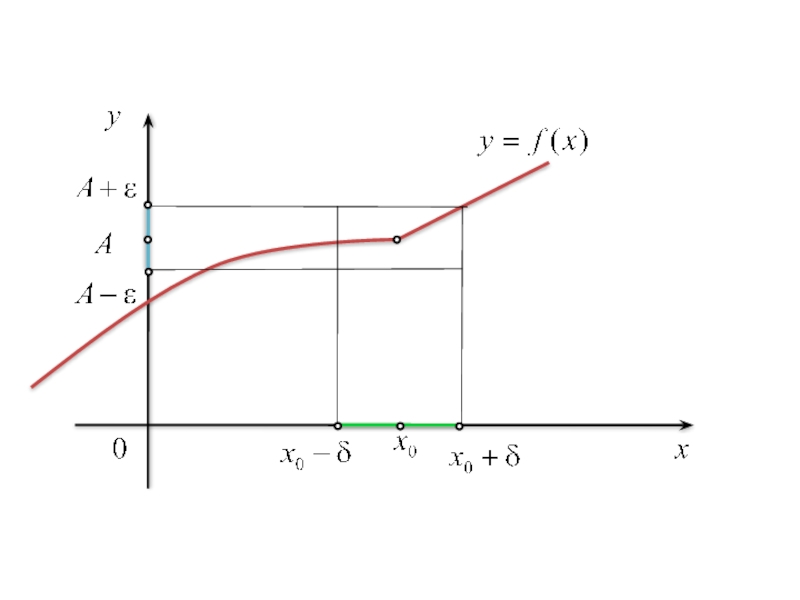
Слайд 41Число А називають границею функції в точці х0,
якщо
виконується нерівність
Слайд 46Функцію f (х), задану на всій числовій прямій, при х →x0
Нескінченно малою величиною називається змінна величина, границя якої дорівнює нулю.
Слайд 47Функцію f (х), задану на всій числовій прямій, при х →∞
Слайд 48 3.7. Основні теореми про границі
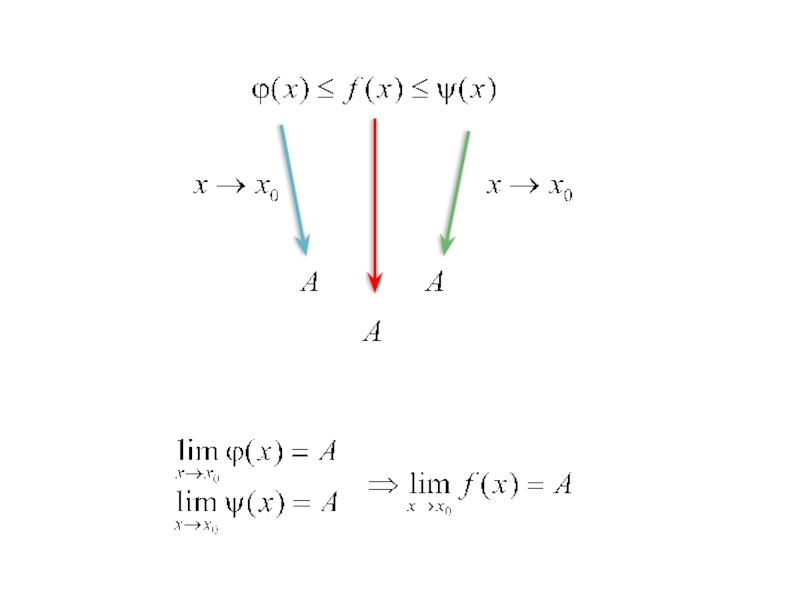
Теорема 1 (про границю суми, добутку
Слайд 59
Озн. Функція f(х) називається неперервною в точці х0,
якщо границя функції
1. Функція визначена в точці х0 і в деякому околі цієї точки;
2. Існує границя ;
3. Границя функції f(х) в точці х0 і значення функції в цій точці х0 збігаються, тобто виконується рівність (23).
(23)
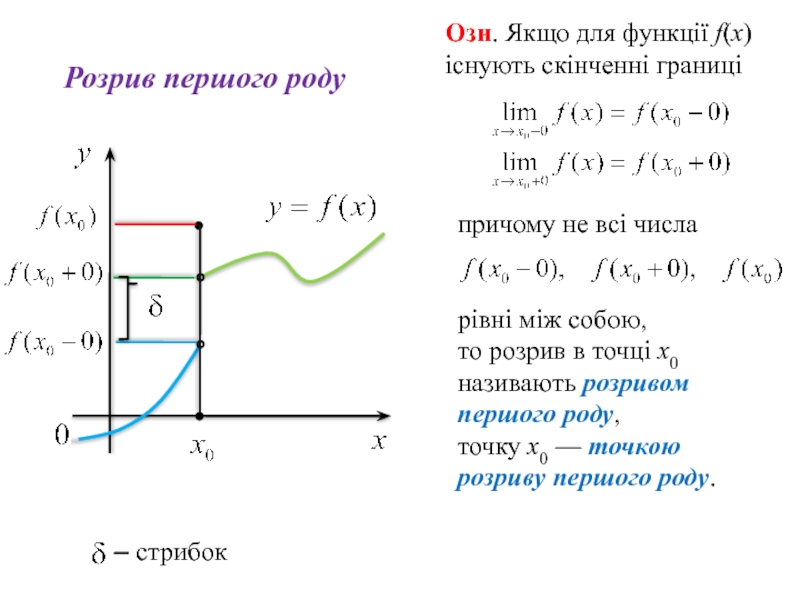
Слайд 62
причому не всі числа
рівні між собою,
то розрив в точці
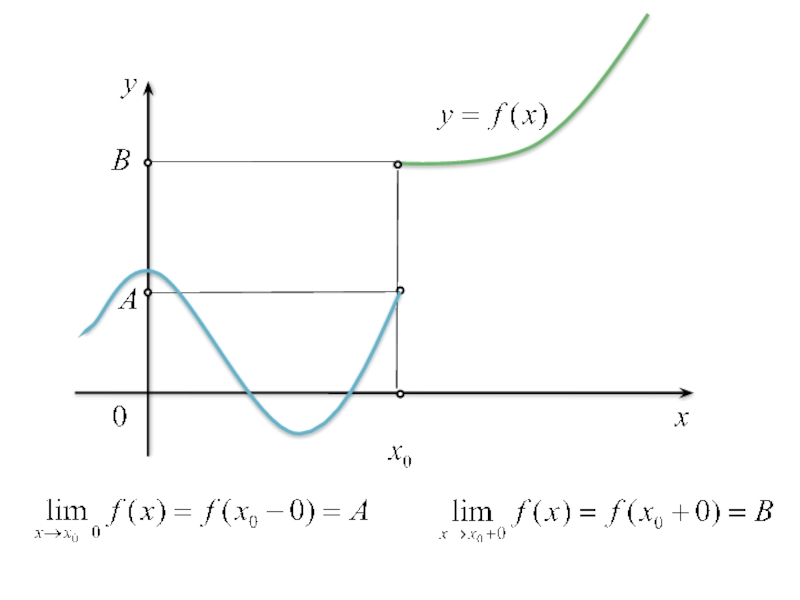
Озн. Якщо для функції f(х) існують скінченні границі
Розрив першого роду
– стрибок
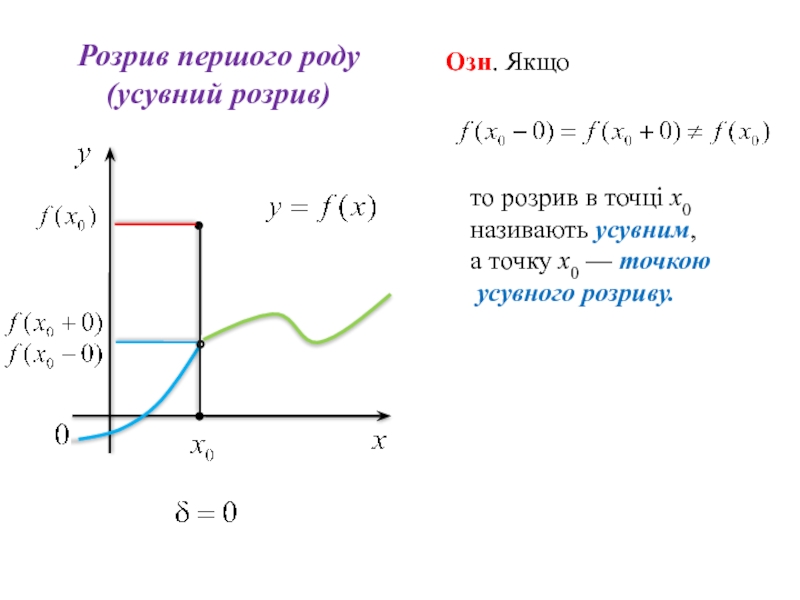
Слайд 63
то розрив в точці х0 називають усувним,
а точку х0 —
Озн. Якщо
Розрив першого роду
(усувний розрив)
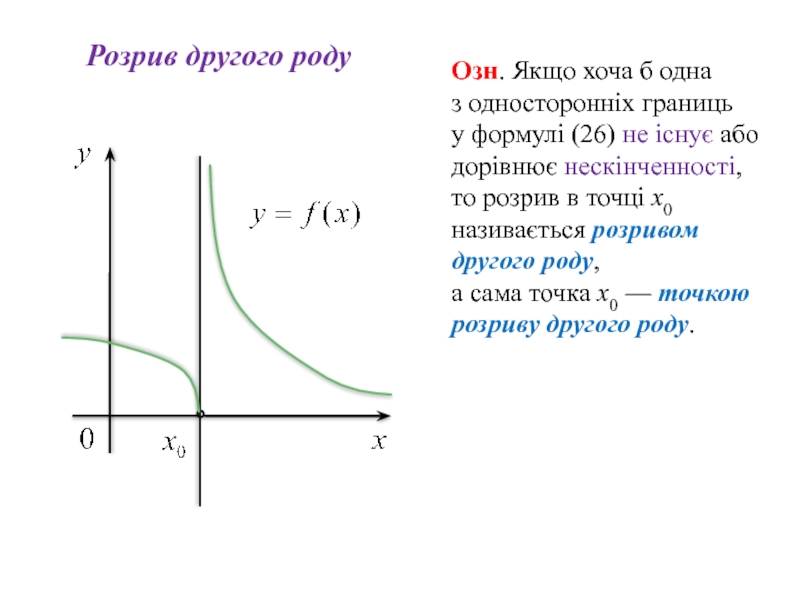
Слайд 64
Озн. Якщо хоча б одна
з односторонніх границь
у формулі (26)
Розрив другого роду
Слайд 65
Теорема. Якщо функції f(х) і φ(х) неперервні в точці х0 ,
5.2. Дії над неперервними функціями. Неперервність елементарних функцій
Теорема. Всяка елементарна функція неперервна в кожній точці, в якій вона визначена.
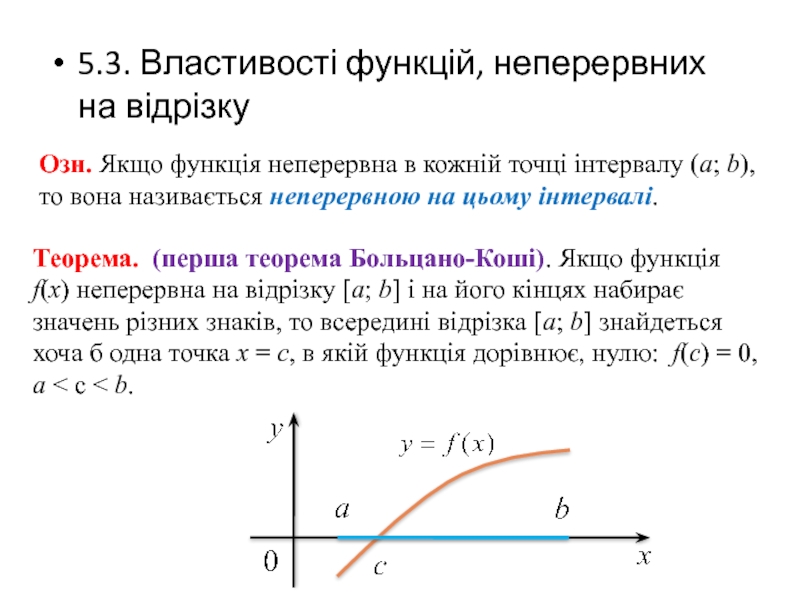
Слайд 66
Озн. Якщо функція неперервна в кожній точці інтервалу (a; b), то
5.3. Властивості функцій, неперервних на відрізку
Теорема. (перша теорема Больцано-Коші). Якщо функція f(х) неперервна на відрізку [a; b] і на його кінцях набирає значень різних знаків, то всередині відрізка [a; b] знайдеться хоча б одна точка х = с, в якій функція дорівнює, нулю: f(с) = 0,
a < с < b.
Слайд 67
Теорема. (друга теорема Больцано-Коші). Нехай функція неперервна на відрізку [a; b]
Слайд 68
Теорема. (Вейєрштрасса). Якщо функція f (х) неперервна на відрізку [a; b],
Слайд 69§1. Похідна
1.1. Задачі, які приводять до поняття похідної
Глава 5
Диференціальне числення функцій
Задача про швидкість прямолінійного руху
Слайд 71
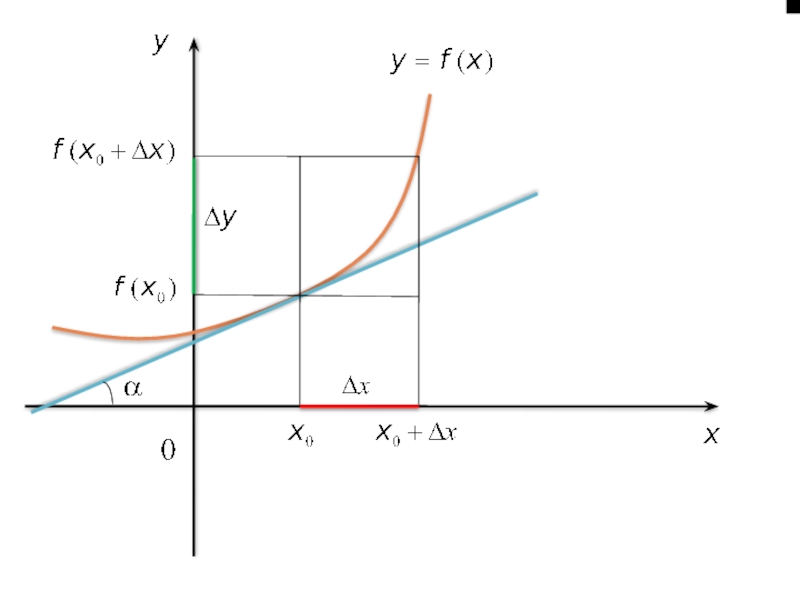
1.2. Означення похідної. Механічний, фізичний та геометричний зміст похідної
Озн. Похідною функції
Слайд 74Швидкість в даний момент часу — це похідна від пройденого шляху
Це механічний зміст похідної. Узагальнюючи, можна сказати: якщо функція у = f (х) описує деякий фізичний процес, то похідна у' = f' (х) є швидкістю зміни цього процесу. В цьому полягає фізичний зміст похідної.
Кутовий коефіцієнт дотичної до кривої у = f (х) в точці М0(х0; у0) або тангенс кута α, що утворює дотична до кривої в даній точці з додатним напрямом осі Ох,— це похідна f' (х0) в цій точці:
k = tg α = f' (х0).
У цьому полягає геометричний зміст похідної.
Слайд 77Озн. Функція f (х) називається диференційовною в точці х0, якщо в
Озн. Функцію f (х) називають диференційовною на проміжку, якщо вона диференційовна в кожній точці цього проміжку.
Теорема. Якщо функція f (х) диференційовна в точці х0,
то вона в цій точці неперервна.






















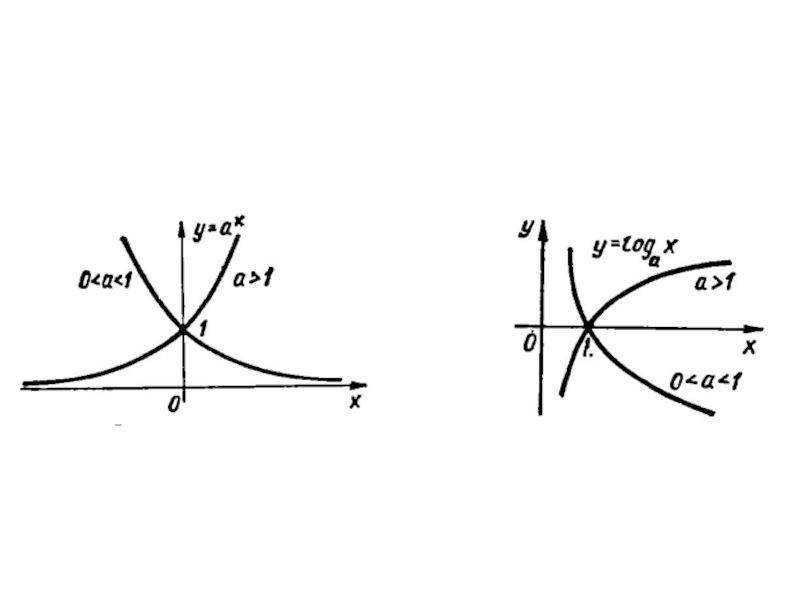















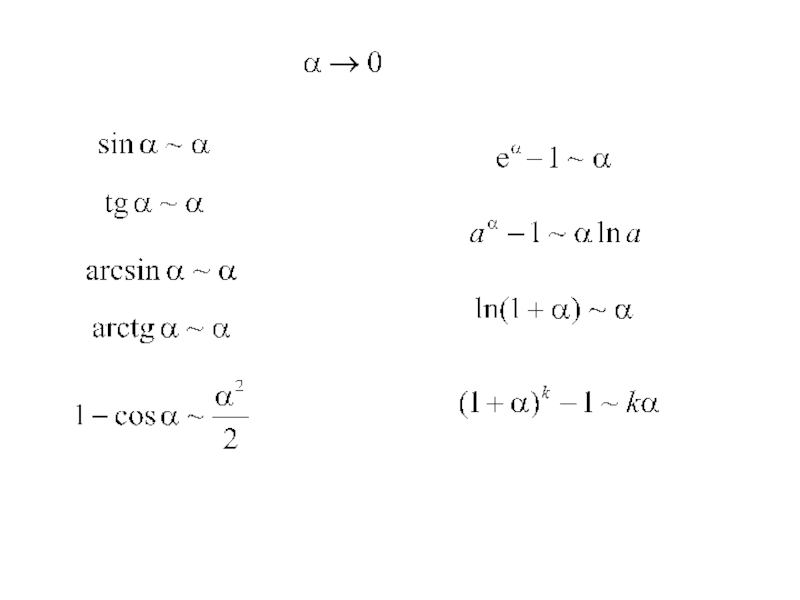


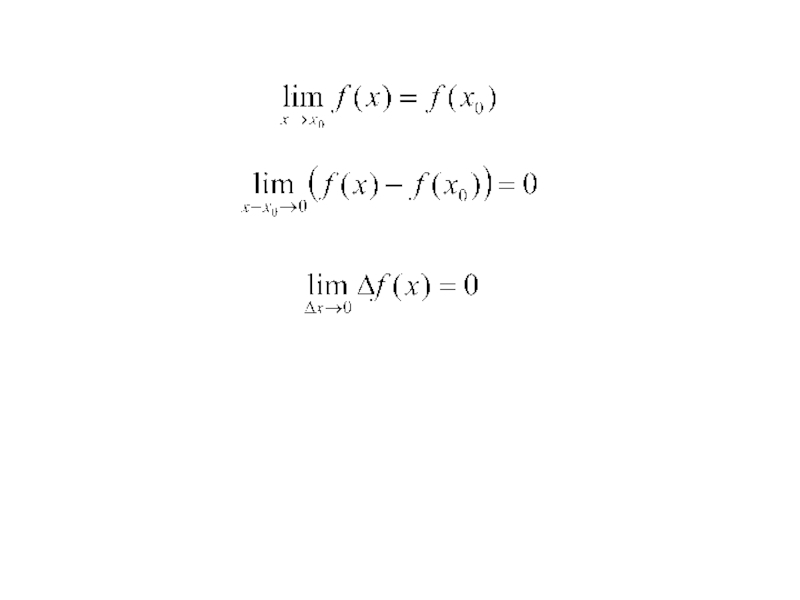
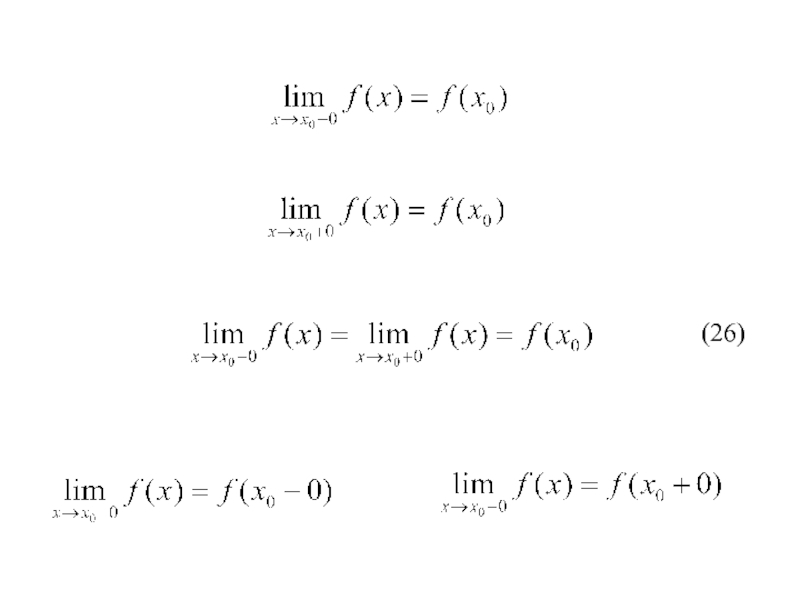

![Теорема. (друга теорема Больцано-Коші). Нехай функція неперервна на відрізку [a; b] і набуває, на його](/img/tmb/1/67110/e6e7506150ae3cf116958923974b982c-800x.jpg)
![Теорема. (Вейєрштрасса). Якщо функція f (х) неперервна на відрізку [a; b], то серед її значень](/img/tmb/1/67110/1ddc75470150332273556e65bdcee50c-800x.jpg)