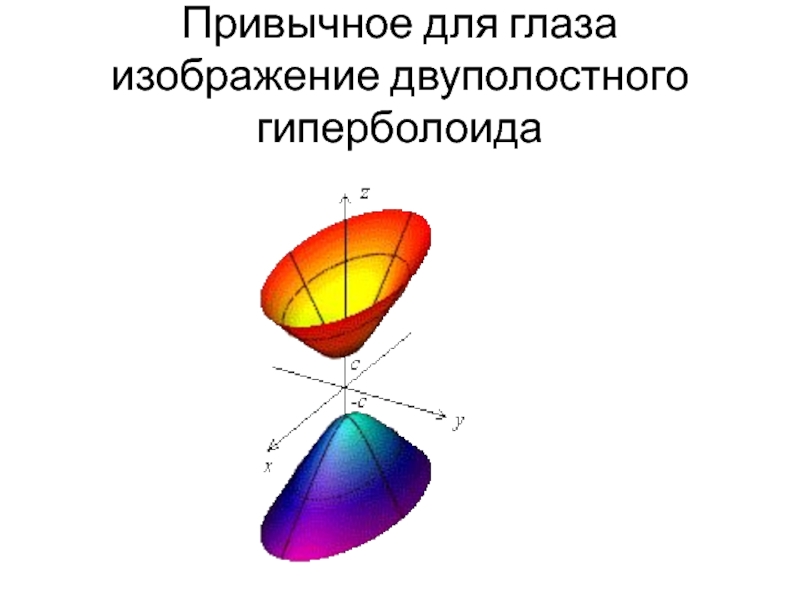
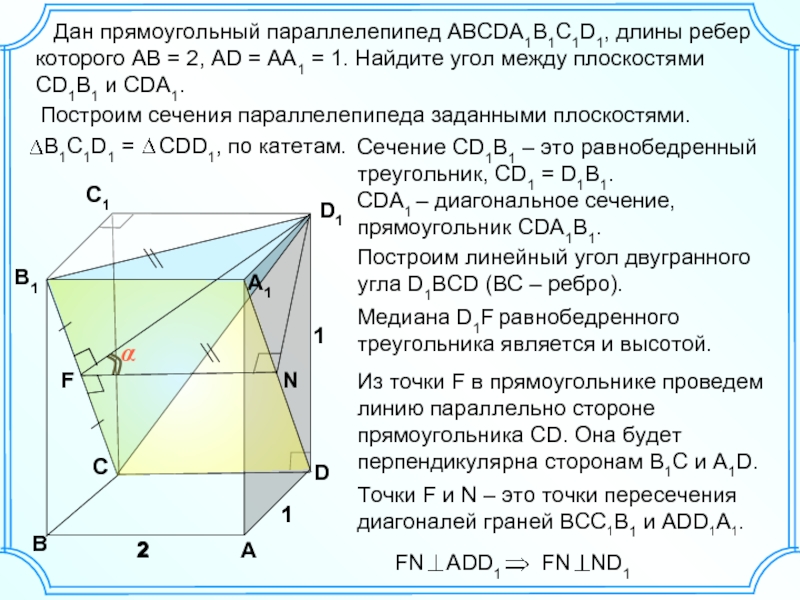
Исследуем форму двуполостного гиперболоида. Так же, как эллипсоид и однополостный гиперболоид, он имеет три плоскости симметрии, три оси симметрии и центр симметрии. Ими являются соответственно координатные плоскости, координатные оси и начало координат.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Двуполостный гиперболоид презентация
Содержание
Для построения гиперболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью . На этой плоскости , поэтому
Слайд 1Двуполостный гиперболоид
Двуполостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид
или
где
- положительные числа.
Слайд 2Для построения гиперболоида найдем его сечения различными плоскостями. Найдем линию пересечения
с плоскостью .
На этой плоскости , поэтому
На этой плоскости , поэтому
Координаты ни одной точки плоскости не могут удовлетворять данному уравнению. Следовательно, двуполостный гиперболоид не пересекает эту плоскость.
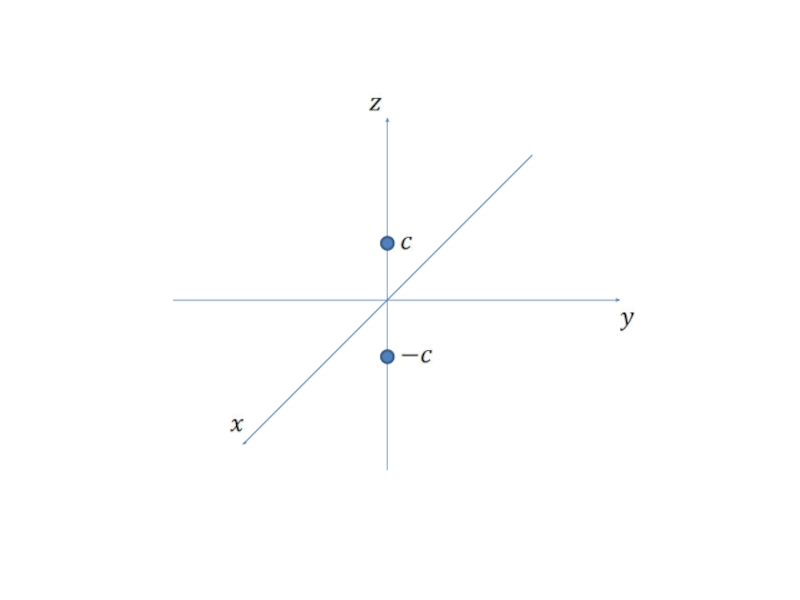
Слайд 3
При
получаем
Плоскость имеет с исследуемой поверхностью точки и . Эти точки называются вершинами гиперболоида.
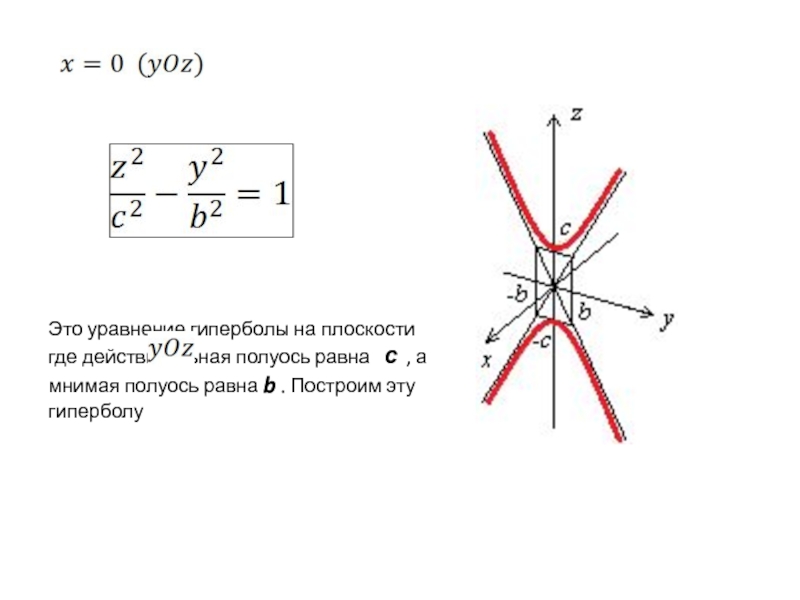
Слайд 6
Это уравнение гиперболы на плоскости
, где действительная полуось равна с , а мнимая полуось равна b . Построим эту гиперболу
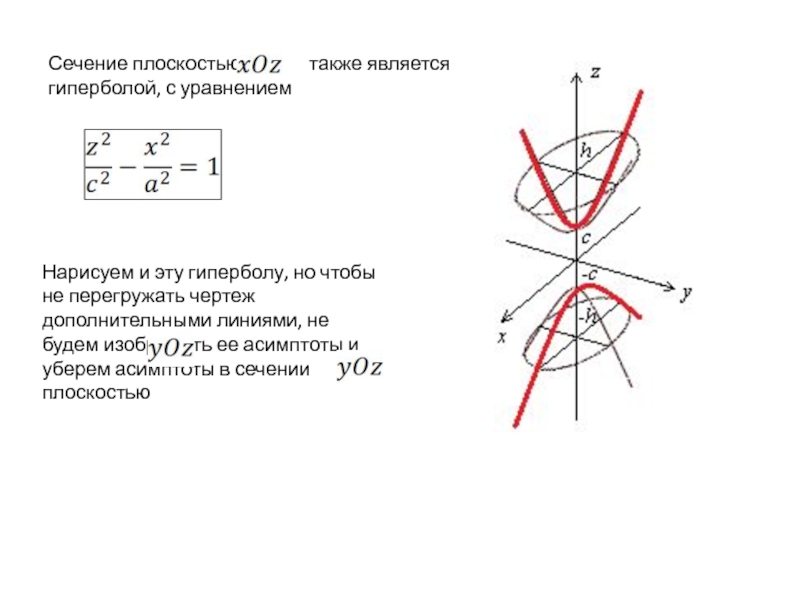
Слайд 7Сечение плоскостью также является гиперболой,
с уравнением
Нарисуем и эту гиперболу, но чтобы не перегружать чертеж дополнительными линиями, не будем изображать ее асимптоты и уберем асимптоты в сечении плоскостью
