- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дополнительные признаки равенства треугольников презентация
Содержание
- 1. Дополнительные признаки равенства треугольников
- 2. Для доказательства используются признаки равенства прямоугольных треугольников.
- 3. Дано: △ ABC и △ A1B1C1, ∠С
- 4. Доказательство: Прямоугольные △ ABH и △
- 5. Если две стороны и медиана, заключенная между
- 6. Дано: △ ABC и △ A1B1C1, AC
- 7. Доказательство: Продолжим медианы и отложим отрезки
- 8. D D1 назад M M1
- 9. Если сторона и две медианы, проведенные к
- 10. Дано: △ ABC и △ A1B1C1, AB
- 11. Доказательство: Точки O и O1 пересечения
- 12. Если две стороны и биссектриса, заключенная между
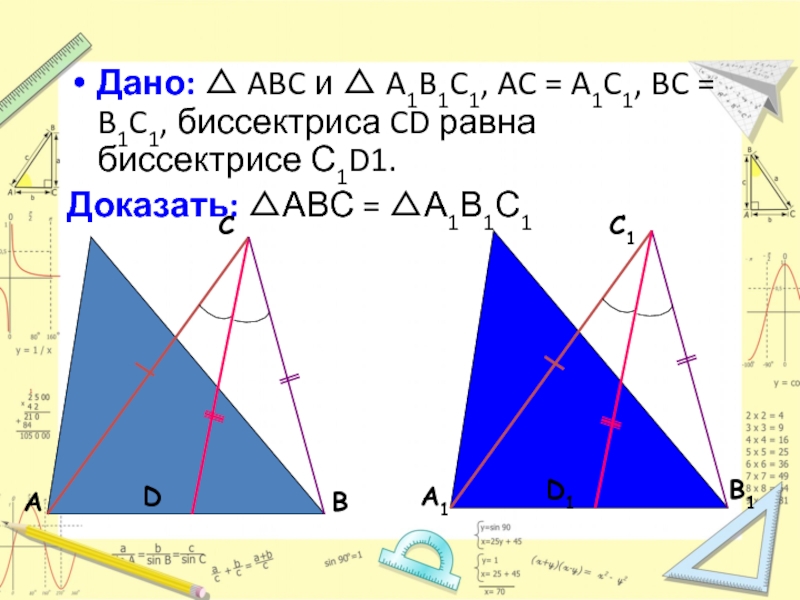
- 13. Дано: △ ABC и △ A1B1C1, AC
- 14. Доказательство: Продолжим стороны AC и
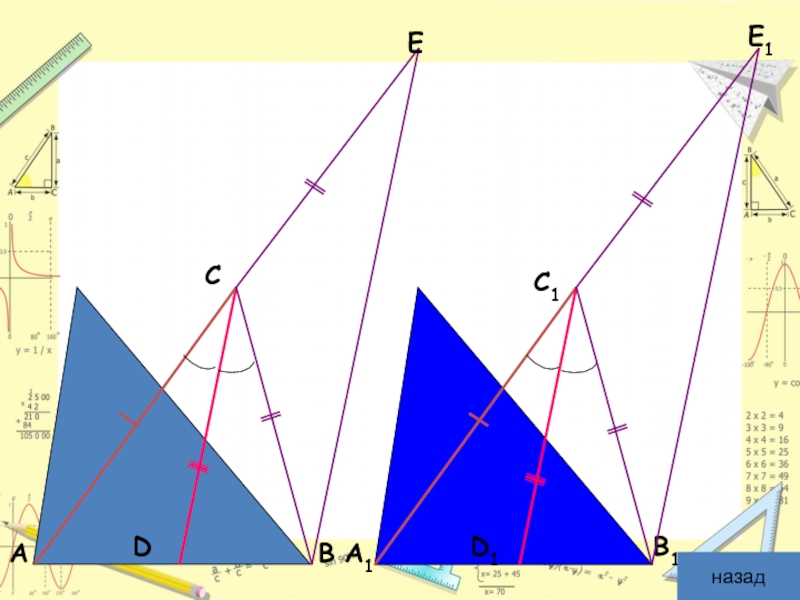
- 15. D D1 E E1 назад
- 16. Два треугольника равны, если сторона, медиана и
- 17. Дано: △ ABC и △ A1B1C1, AC
- 18. Доказательство: Прямоугольные △ ACH = △A1C1H1
- 19. Два треугольника равны, если медиана и два
- 20. A B C
- 21. Доказательство: В данных треугольниках удвоим медианы
- 22. Два треугольника равны, если сторона, и две
- 23. Дано: △ ABC и △ A1B1C1, AB
- 24. Доказательство: Из равенства прямоугольных треугольников △
- 25. Два треугольника равны, если три медианы одного треугольника соответственно равны трем медианам другого. Теорема 8
- 26. Дано: △ ABC и △ A1B1C1, медианы
- 27. Доказательство: Пусть O и O1 —
- 28. Два треугольника равны, если три высоты одного
- 29. Дано: △ ABC и △ A1B1C1, AB
- 30. Доказательство: Обозначим стороны треугольников соответственно a,
Слайд 1Дополнительные признаки равенства треугольников
Серова Наталья Александровна,
Мурзина Наталья Викторовна,
учителя математики,
г.Омск МОУ «Средняя общеобразовательная школа № 16»
Слайд 2Для доказательства используются признаки равенства прямоугольных треугольников.
Если угол, сторона, противолежащая этому
Теорема 1
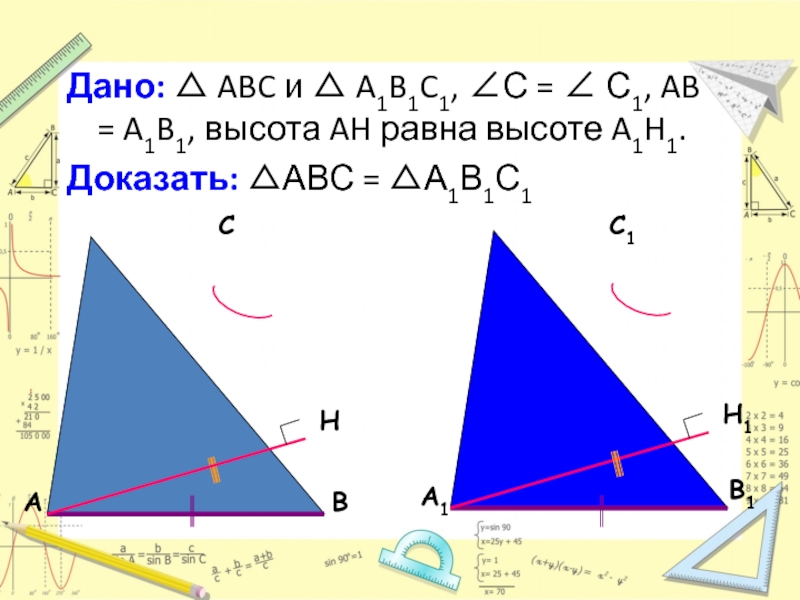
Слайд 3Дано: △ ABC и △ A1B1C1, ∠С = ∠ С1, AB
Доказать: △АВС = △А1В1С1
H
H1
Слайд 4Доказательство:
Прямоугольные △ ABH и △ A1B1H1 равны по катету и
AB = A1B1, ∠ A = ∠ A1, ∠ B = ∠ B1.
Следовательно, эти треугольники равны по второму признаку равенства треугольников.
Слайд 5Если две стороны и медиана, заключенная между ними, одного треугольника соответственно
Теорема 2
Теорема 8
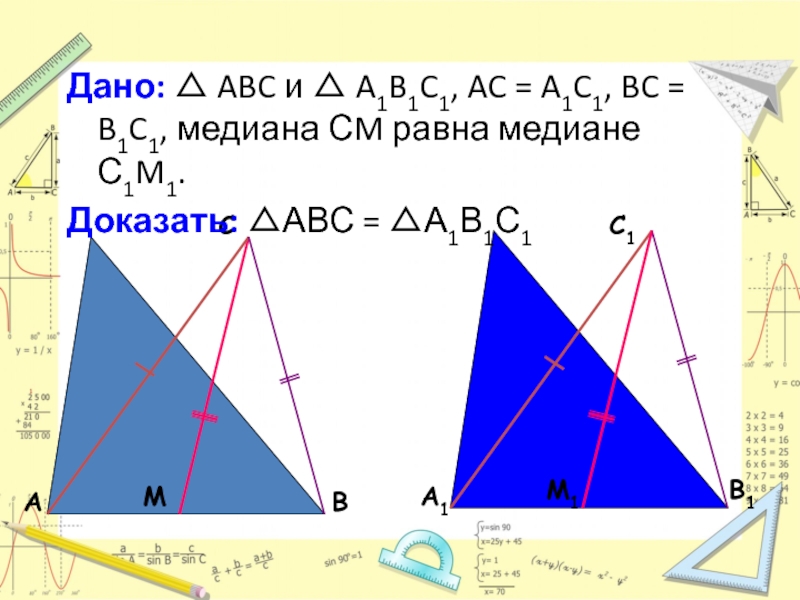
Слайд 6Дано: △ ABC и △ A1B1C1, AC = A1C1, BC =
Доказать: △АВС = △А1В1С1
M
M1
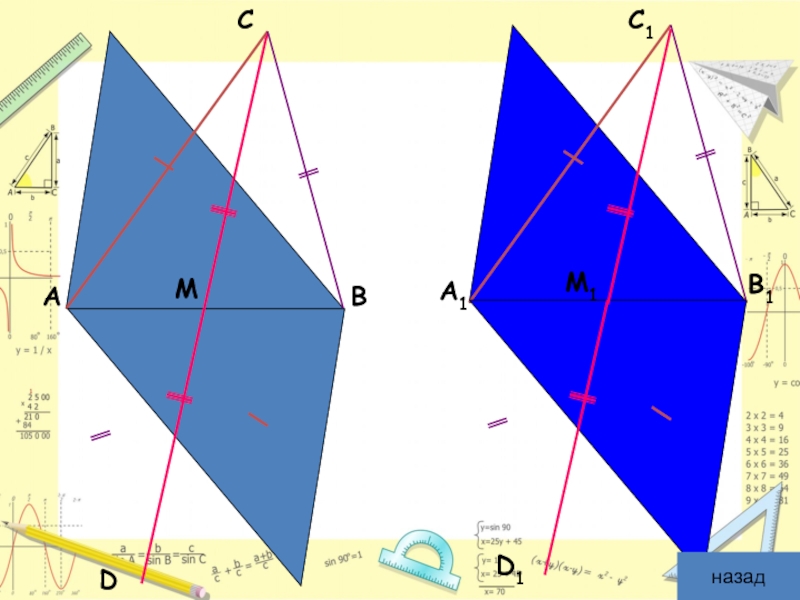
Слайд 7Доказательство:
Продолжим медианы и отложим отрезки MD = CM и M1D1
Аналогично, △ BCD = △ B1C1D1 по трем сторонам. Следовательно, ∠ BCD = ∠B1C1D1.
Значит, ∠ С = ∠ С1 и треугольники ABC и A1B1C1 равны по двум сторонам и углу между ними (по первому признаку равенства треугольников).
чертеж
Слайд 9Если сторона и две медианы, проведенные к двум другим сторонам, одного
Теорема 3
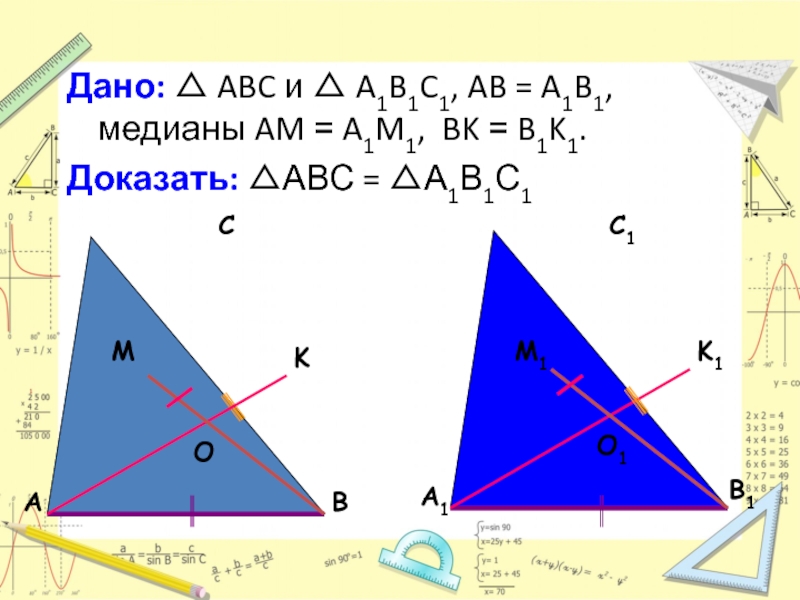
Слайд 10Дано: △ ABC и △ A1B1C1, AB = A1B1, медианы AM
Доказать: △АВС = △А1В1С1
M
M1
K
K1
O
O1
Слайд 11Доказательство:
Точки O и O1 пересечения медиан данных треугольников делят медианы
Аналогично доказывается, что ∠ BAC = ∠B1A1C1.
Таким образом, треугольники △ ABC и △ A1B1C1 равны по стороне и двум прилежащим к ней углам. Следовательно, △АВС = △А1В1С1 равны по второму признаку равенства треугольников.
Слайд 12Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно
Теорема 4
Слайд 13Дано: △ ABC и △ A1B1C1, AC = A1C1, BC =
Доказать: △АВС = △А1В1С1
D
D1
Слайд 14Доказательство:
Продолжим стороны AC и A1C1 и отложим на их продолжениях
Тогда ,
BCE =△ B1C1E1 по трем сторонам. Значит, ∠ E = ∠ E1 и BE = B1E1.
ABE = △ A1B1E1 по двум сторонам и углу между ними. Значит, AB = A1B1.
Таким образом, △ ABC = △A1B1C1 по трем сторонам (3 признак равенства треугольников).
чертеж
Слайд 16Два треугольника равны, если сторона, медиана и высота, проведенные к другой
Теорема 5
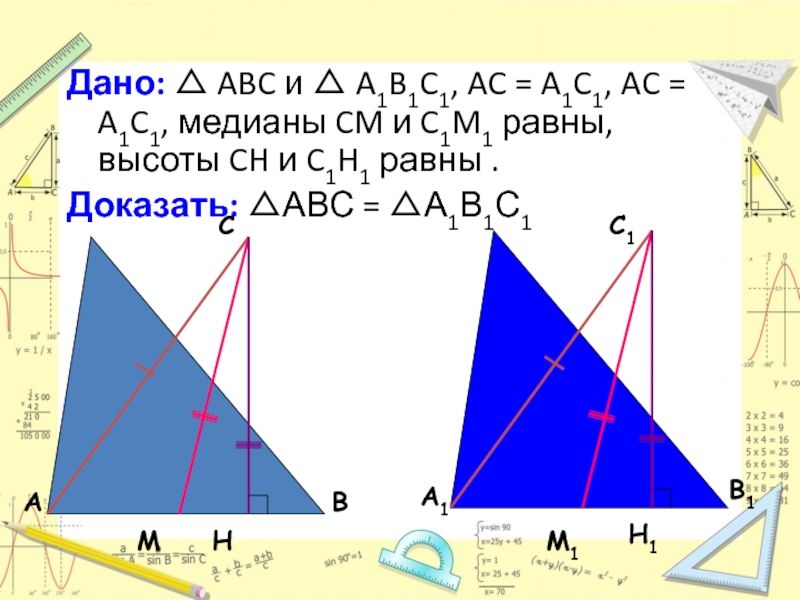
Слайд 17Дано: △ ABC и △ A1B1C1, AC = A1C1, AC =
Доказать: △АВС = △А1В1С1
M
M1
H
H1
Слайд 18Доказательство:
Прямоугольные △ ACH = △A1C1H1 по гипотенузе и катету. Следовательно,
Слайд 19Два треугольника равны, если медиана и два угла на которые делит
Теорема 6
Слайд 20
A
B
C
M
B1
A1
M1
C1
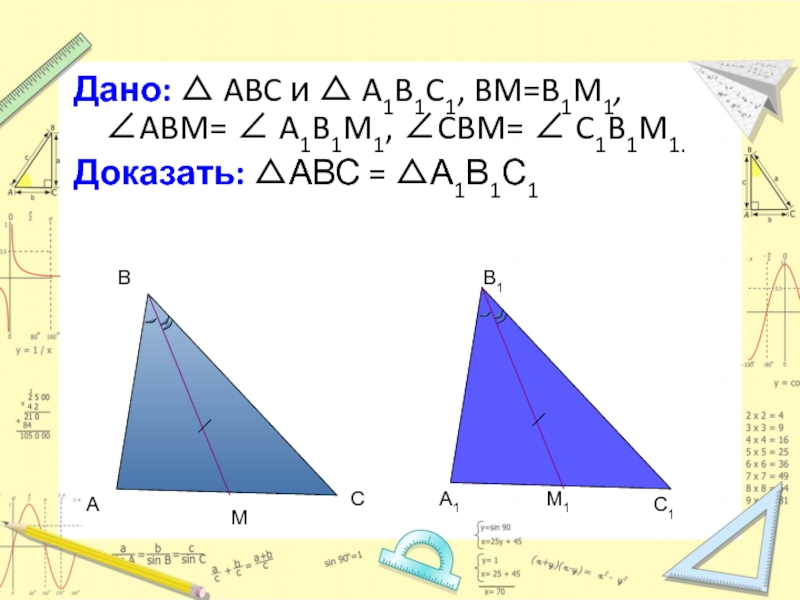
Дано: △ ABC и △ A1B1C1, BM=B1M1, ∠ABM= ∠ A1B1M1, ∠CBM=
Доказать: △АВС = △А1В1С1
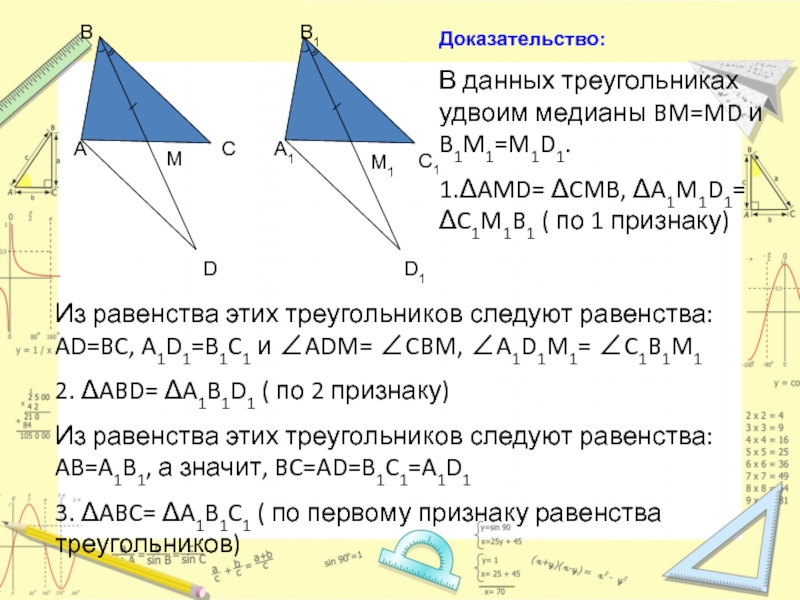
Слайд 21Доказательство:
В данных треугольниках удвоим медианы BM=MD и B1M1=M1D1.
1.ΔAMD= ΔCMB,
Из равенства этих треугольников следуют равенства: AD=BC, A1D1=B1C1 и ∠ADM= ∠CBM, ∠A1D1M1= ∠C1B1M1
2. ΔABD= ΔA1B1D1 ( по 2 признаку)
Из равенства этих треугольников следуют равенства: AB=A1B1, а значит, BC=AD=B1C1=A1D1
3. ΔABC= ΔA1B1C1 ( по первому признаку равенства треугольников)
Слайд 22Два треугольника равны, если сторона, и две высоты, опущенные на две
Теорема 7
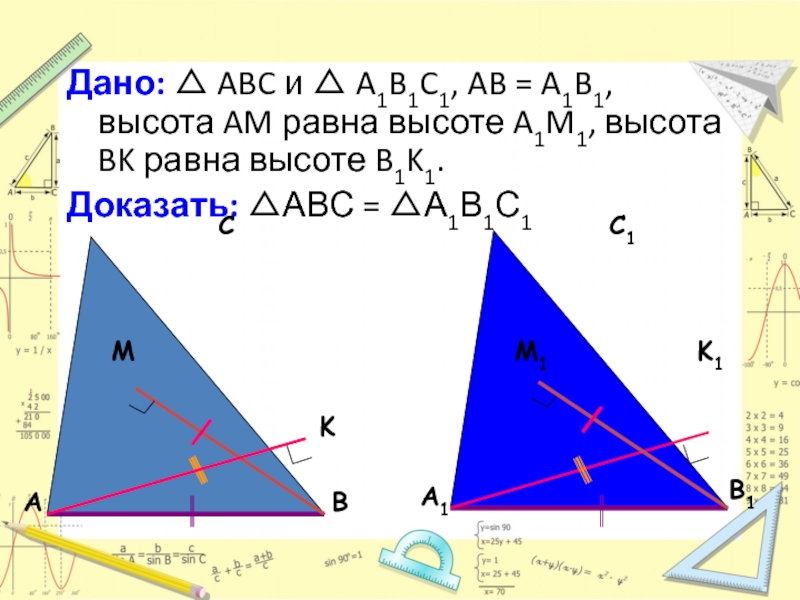
Слайд 23Дано: △ ABC и △ A1B1C1, AB = A1B1, высота AM
Доказать: △АВС = △А1В1С1
M
M1
K
K1
Слайд 24Доказательство:
Из равенства прямоугольных треугольников △ AMB = △ A1M1B1, △
Поэтому △ ABC = △ A1B1C1 по стороне ( AB = A1B1) и двум прилежащим к ней углам (по второму признаку равенства треугольников).
Слайд 25Два треугольника равны, если три медианы одного треугольника соответственно равны трем
Теорема 8
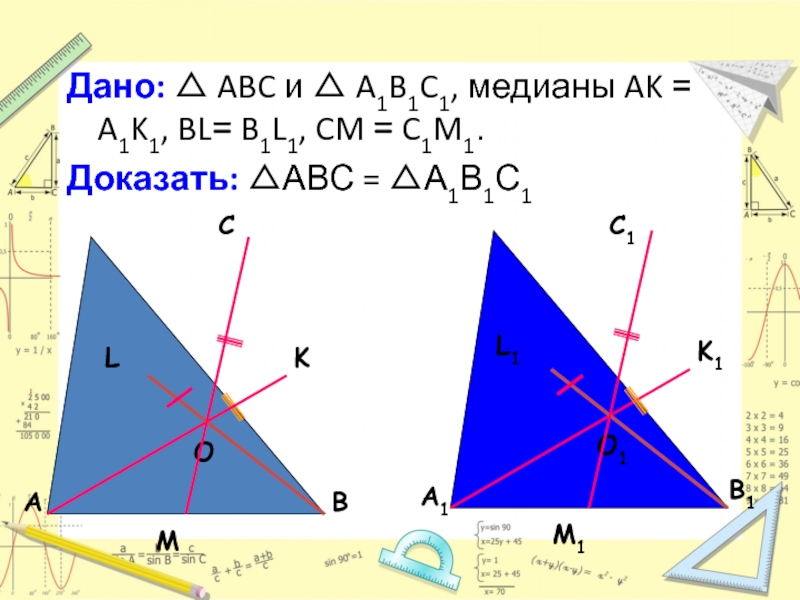
Слайд 26Дано: △ ABC и △ A1B1C1, медианы AK = A1K1, BL=
Доказать: △АВС = △А1В1С1
M
M1
K
K1
O
O1
L
L1
Слайд 27Доказательство:
Пусть O и O1 — точки пересечения медиан данных треугольников.
По признаку равенства треугольников, доказанному нами под номером 2, △ ABO = △ A1B1O1, значит, AB = A1B1.
Аналогично доказывается, что BC = B1C1 и AC = A1C1.
Таким образом, △ ABC и △ A1B1C1 равны по трем сторонам ( по третьему признаку равенства треугольников) .
Слайд 28Два треугольника равны, если три высоты одного треугольника соответственно равны трем
Теорема 9
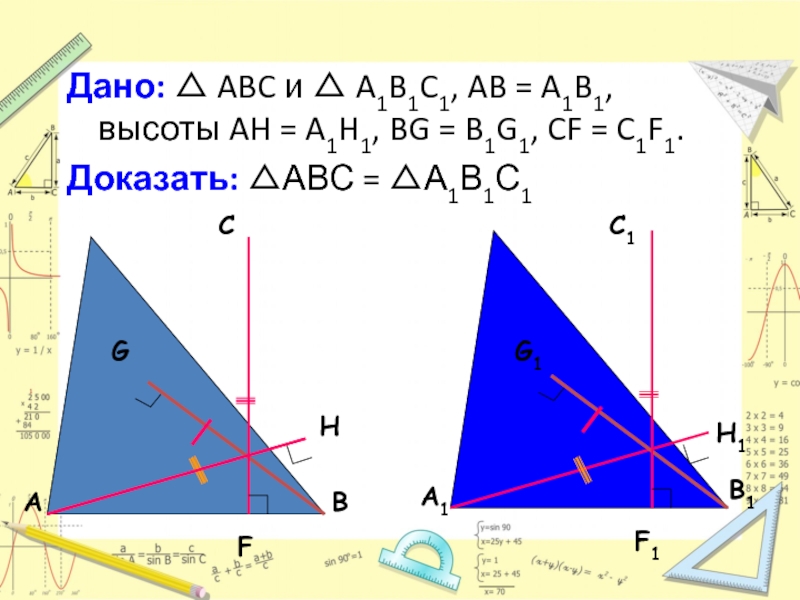
Слайд 29Дано: △ ABC и △ A1B1C1, AB = A1B1, высоты AH
Доказать: △АВС = △А1В1С1
G
G1
H
H1
F
F1
Слайд 30Доказательство:
Обозначим стороны треугольников соответственно a, b, c и a1, b1,
Имеют место равенства aha = bhb = chc и a1h1a = b1h1b = c1h1c. Разделив почленно первые равенства на вторые, получим равенства
из которых следует, что треугольники ABC и A1B1C1 подобны. А так как соответствующие высоты этих треугольников равны, то они не только подобны, но и равны.