Дискретная математика. Деревья. Определения дерева презентация

Содержание

1. Дискретная математика. Деревья. Определения дерева
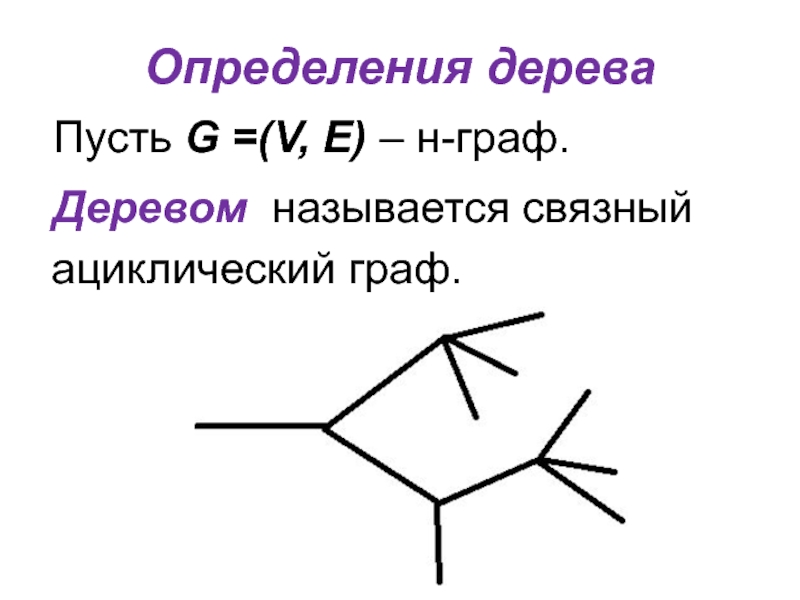
2. Определения дерева Пусть
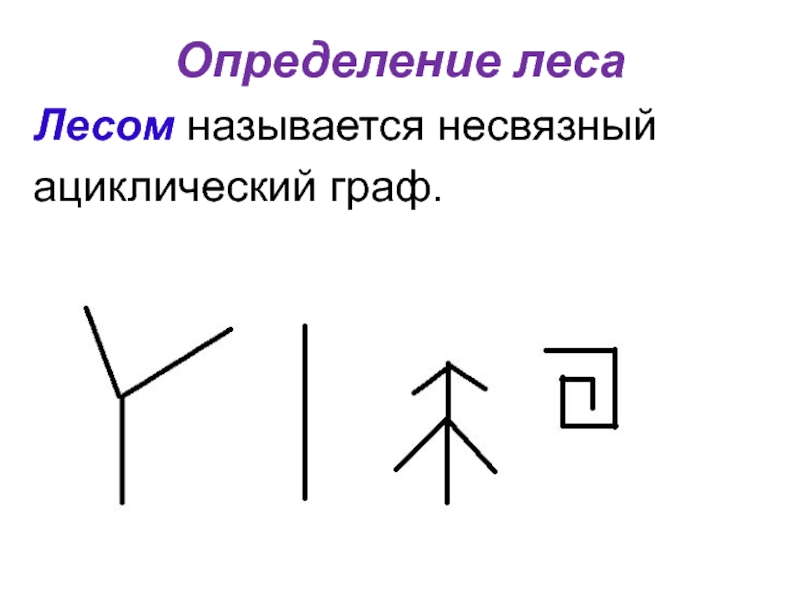
3. Определение леса Лесом называется несвязный ациклический граф.
4. Теорема 1 Граф
5. Терема 2 Граф
6. Бинарное дерево Бинарным деревом называется ориентированное дерево
7. Корень дерева Если
8. Корень дерева У всех вершин дерева локальные
10. Вершины максимального типа Дано неориентированное дерево Т.
11. Вершины максимального типа Удалим из дерева Т
12. Вершины максимального типа Удалим из дерева Т1
13. Вершины максимального типа Утверждение 1 В конечном
14. Вершины максимального типа Утверждение 1 В конечном
15. Вершины максимального типа Утверждение 3 Центрами
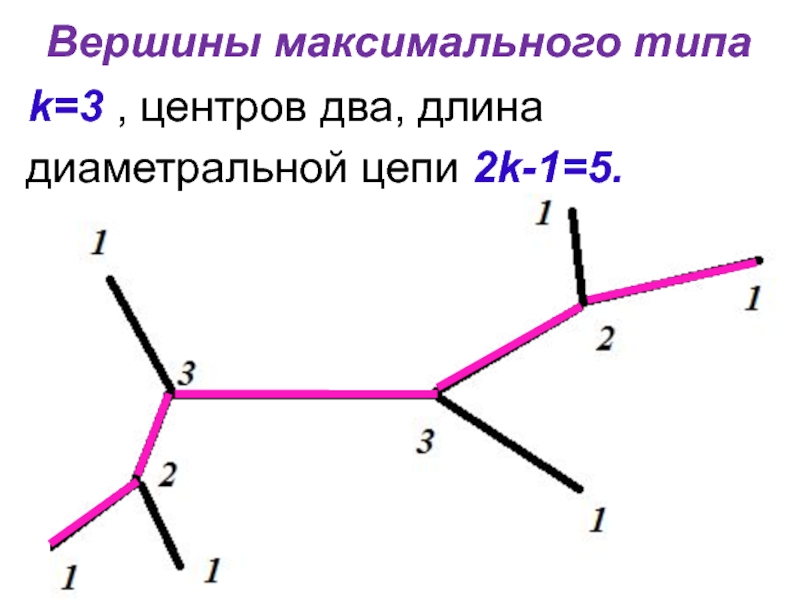
16. Вершины максимального типа k=3 , центров два, длина диаметральной цепи 2k-1=5.
17. Ветвь дерева Ветвью вершины а в дереве
18. Ветвь t

Главная
Математика
Дискретная математика. Деревья. Определения дерева

Слайд 1Деревья
Дискретная математика

Слайд 2

Определения дерева
Пусть G =(V, E) – н-граф.
Деревом называется связный ациклический граф.

Слайд 3

Определение леса
Лесом называется несвязный ациклический граф.

Слайд 4

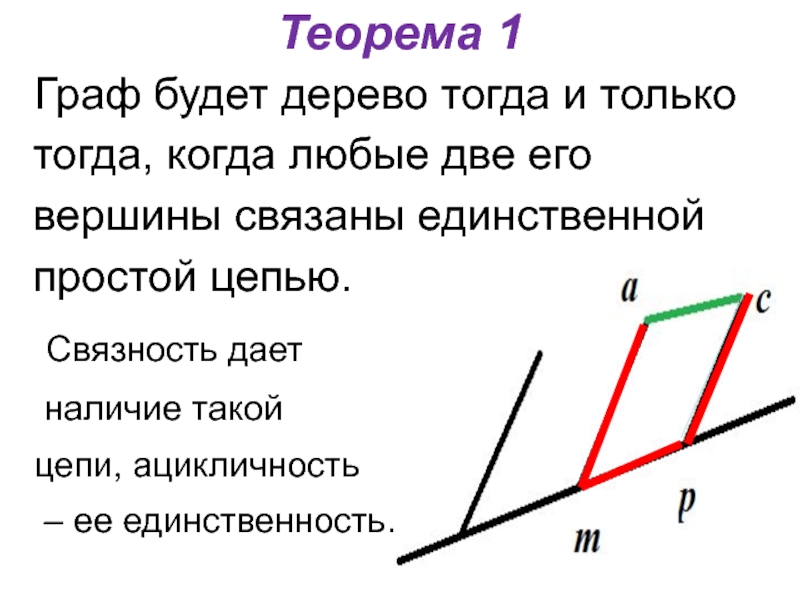
Теорема 1
Граф будет дерево тогда и только тогда, когда любые две

его вершины связаны единственной простой цепью.
Связность дает
наличие такой
цепи, ацикличность
– ее единственность.

Слайд 5

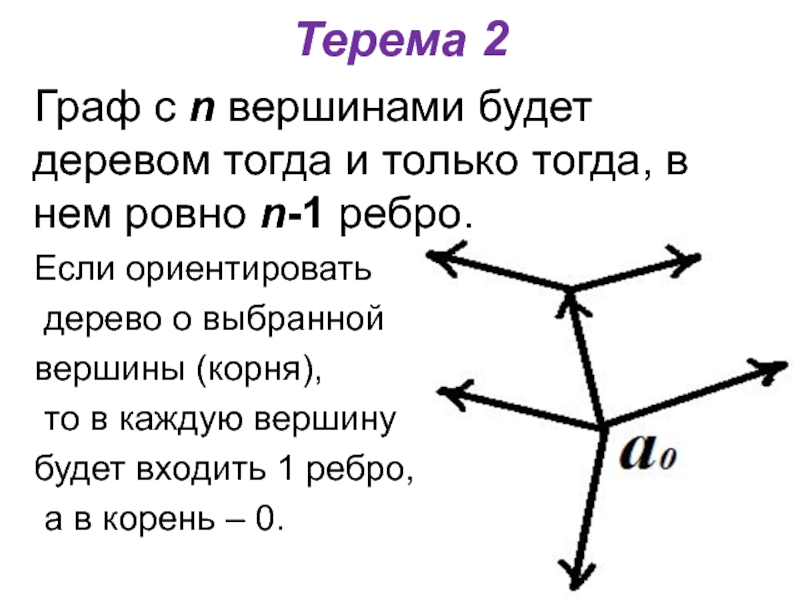
Терема 2
Граф с n вершинами будет деревом тогда и только тогда,

в нем ровно n-1 ребро.
Если ориентировать
дерево о выбранной
вершины (корня),
то в каждую вершину
будет входить 1 ребро,
а в корень – 0.

Слайд 6Бинарное дерево
Бинарным деревом называется ориентированное дерево с корнем, где каждая вершина

имеет локальную степень исхода, равную 2.

Слайд 7

Корень дерева
Если дерево неориентированно, то его можно ориентировать от корня. Корень

– это любая выделенная вершина.

Слайд 8Корень дерева
У всех вершин дерева локальные степени захода равны 1, а

у корня 0.
Вершины, степени исхода которых равны 0 называются листьями
Высотой дерева называется наибольшее расстояние от корня до листа.

Слайд 9

Слайд 10Вершины максимального типа
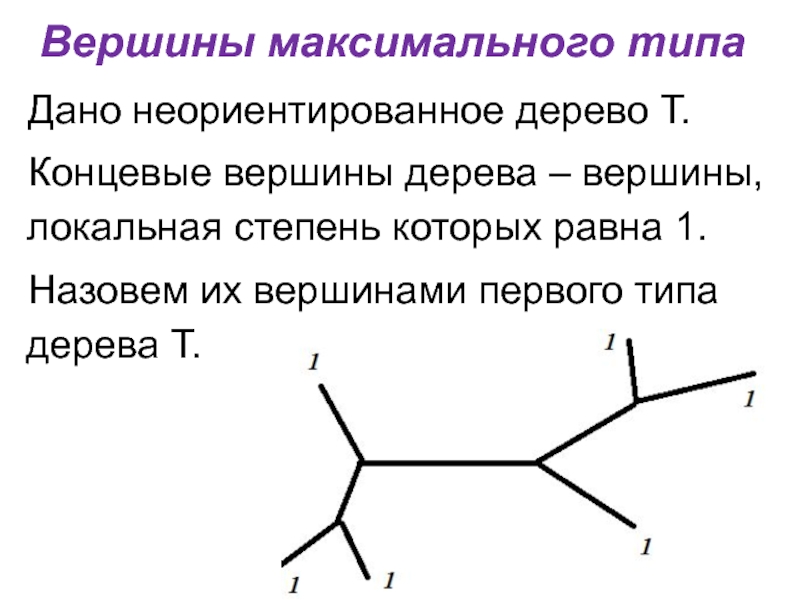
Дано неориентированное дерево Т.
Концевые вершины дерева – вершины, локальная

степень которых равна 1.
Назовем их вершинами первого типа дерева Т.

Слайд 11Вершины максимального типа
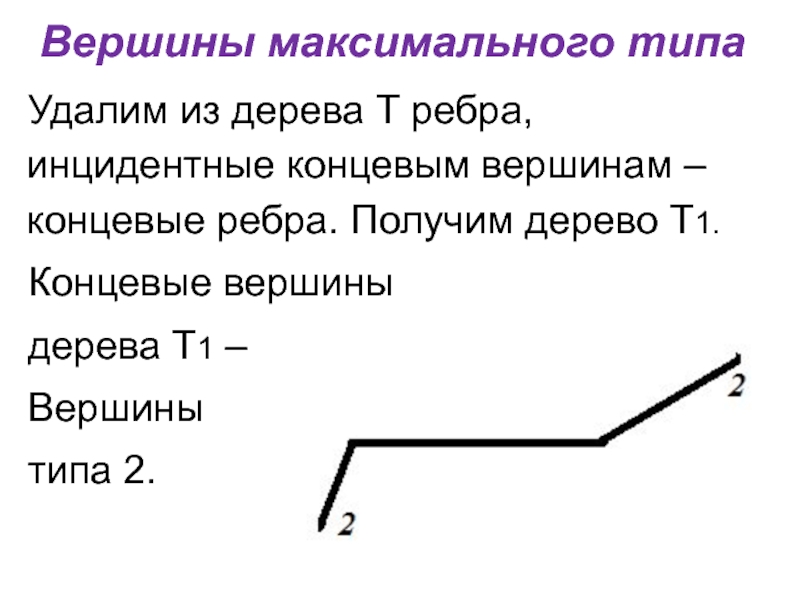
Удалим из дерева Т ребра, инцидентные концевым вершинам –

концевые ребра. Получим дерево Т1.
Концевые вершины
дерева Т1 –
Вершины
типа 2.

Слайд 12Вершины максимального типа
Удалим из дерева Т1 концевые ребра. Получим дерево Т2.

Концевые вершины
дерева Т2 –
Вершины
типа 3.

Слайд 13Вершины максимального типа
Утверждение 1
В конечном дереве есть вершины только конечного числа

типов.
Утверждение 2
Вершин максимального типа k одна или две.

Слайд 14Вершины максимального типа
Утверждение 1
В конечном дереве есть вершины только конечного числа

типов.
Утверждение 2
Вершин максимального типа k одна или две.

Слайд 15Вершины максимального типа
Утверждение 3
Центрами деревьев являются вершины максимального типа k

и только они. Все диаметральные цепи проходят через центры.
Длина диаметральной цепи равна 2k-1, если центра два и 2k-2, если центр один.

Слайд 16Вершины максимального типа
k=3 , центров два, длина диаметральной цепи 2k-1=5.

Слайд 17Ветвь дерева
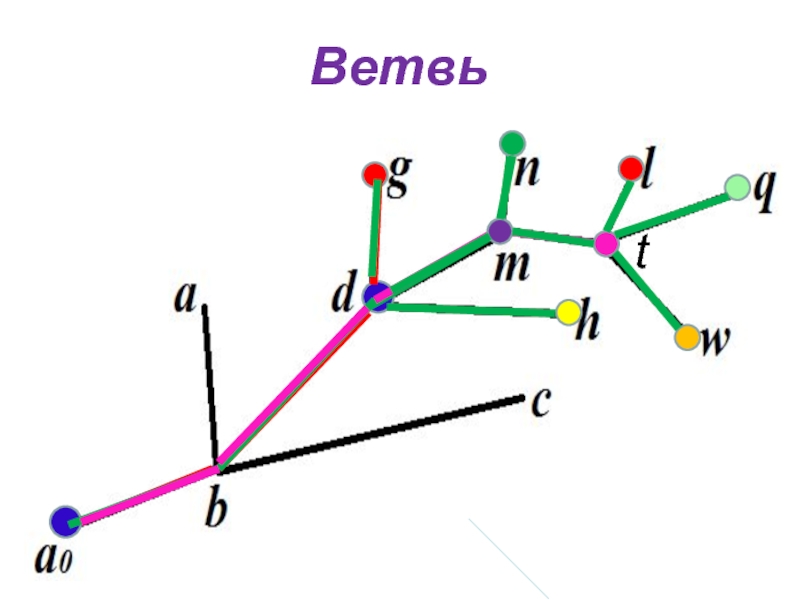
Ветвью вершины а в дереве Т с корнем а0 называется

подграф, порожденный множеством вершин В(а) состоящим из вершин, связанных с корнем цепь, проходящей через а.

Слайд 18Ветвь

t

Скачать презентацию

Дискретная математика. Деревья. Определения дерева презентация

Содержание

Слайд 1Деревья
Дискретная математика

Слайд 2

Определения дерева
Пусть G =(V, E) – н-граф.
Деревом называется связный ациклический граф.

Слайд 3

Определение леса
Лесом называется несвязный ациклический граф.

Слайд 4

Теорема 1
Граф будет дерево тогда и только тогда, когда любые две

Слайд 5

Терема 2
Граф с n вершинами будет деревом тогда и только тогда,

Слайд 6Бинарное дерево
Бинарным деревом называется ориентированное дерево с корнем, где каждая вершина

Слайд 7

Корень дерева
Если дерево неориентированно, то его можно ориентировать от корня. Корень

Слайд 8Корень дерева
У всех вершин дерева локальные степени захода равны 1, а

Слайд 9

Слайд 10Вершины максимального типа
Дано неориентированное дерево Т.
Концевые вершины дерева – вершины, локальная

Слайд 11Вершины максимального типа
Удалим из дерева Т ребра, инцидентные концевым вершинам –

Слайд 12Вершины максимального типа
Удалим из дерева Т1 концевые ребра. Получим дерево Т2.

Слайд 13Вершины максимального типа
Утверждение 1
В конечном дереве есть вершины только конечного числа

Слайд 14Вершины максимального типа
Утверждение 1
В конечном дереве есть вершины только конечного числа

Слайд 15Вершины максимального типа
Утверждение 3
Центрами деревьев являются вершины максимального типа k

Слайд 16Вершины максимального типа
k=3 , центров два, длина диаметральной цепи 2k-1=5.

Слайд 17Ветвь дерева
Ветвью вершины а в дереве Т с корнем а0 называется

Слайд 18Ветвь

t

Обратная связь

Что такое ThePresentation.ru?

Дискретная математика. Деревья. Определения дерева презентация

Содержание

Слайд 1ДеревьяДискретная математика

Слайд 2Определения дереваПусть G =(V, E) – н-граф.Деревом называется связный ациклический граф.

Слайд 3Определение лесаЛесом называется несвязный ациклический граф.

Слайд 4Теорема 1Граф будет дерево тогда и только тогда, когда любые две

Слайд 5Терема 2Граф с n вершинами будет деревом тогда и только тогда,

Слайд 6Бинарное деревоБинарным деревом называется ориентированное дерево с корнем, где каждая вершина

Слайд 7Корень дереваЕсли дерево неориентированно, то его можно ориентировать от корня. Корень

Слайд 8Корень дереваУ всех вершин дерева локальные степени захода равны 1, а

Слайд 9

Слайд 10Вершины максимального типаДано неориентированное дерево Т.Концевые вершины дерева – вершины, локальная

Слайд 11Вершины максимального типаУдалим из дерева Т ребра, инцидентные концевым вершинам –

Слайд 12Вершины максимального типаУдалим из дерева Т1 концевые ребра. Получим дерево Т2.

Слайд 13Вершины максимального типаУтверждение 1В конечном дереве есть вершины только конечного числа

Слайд 14Вершины максимального типаУтверждение 1В конечном дереве есть вершины только конечного числа

Слайд 15Вершины максимального типаУтверждение 3 Центрами деревьев являются вершины максимального типа k

Слайд 16Вершины максимального типаk=3 , центров два, длина диаметральной цепи 2k-1=5.

Слайд 17Ветвь дереваВетвью вершины а в дереве Т с корнем а0 называется

Слайд 18Ветвь t

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 1Деревья
Дискретная математика

Слайд 2

Определения дерева
Пусть G =(V, E) – н-граф.
Деревом называется связный ациклический граф.

Слайд 3

Определение леса
Лесом называется несвязный ациклический граф.

Слайд 4

Теорема 1
Граф будет дерево тогда и только тогда, когда любые две

Слайд 5

Терема 2
Граф с n вершинами будет деревом тогда и только тогда,

Слайд 6Бинарное дерево
Бинарным деревом называется ориентированное дерево с корнем, где каждая вершина

Слайд 7

Корень дерева
Если дерево неориентированно, то его можно ориентировать от корня. Корень

Слайд 8Корень дерева
У всех вершин дерева локальные степени захода равны 1, а

Слайд 10Вершины максимального типа
Дано неориентированное дерево Т.
Концевые вершины дерева – вершины, локальная

Слайд 11Вершины максимального типа
Удалим из дерева Т ребра, инцидентные концевым вершинам –

Слайд 12Вершины максимального типа
Удалим из дерева Т1 концевые ребра. Получим дерево Т2.

Слайд 13Вершины максимального типа
Утверждение 1
В конечном дереве есть вершины только конечного числа

Слайд 14Вершины максимального типа
Утверждение 1
В конечном дереве есть вершины только конечного числа

Слайд 15Вершины максимального типа
Утверждение 3
Центрами деревьев являются вершины максимального типа k

Слайд 16Вершины максимального типа
k=3 , центров два, длина диаметральной цепи 2k-1=5.

Слайд 17Ветвь дерева
Ветвью вершины а в дереве Т с корнем а0 называется

Слайд 18Ветвь

t